はじめに
前回からの続編になります.
続編はこちら.
アルゴリズム
SMBO
TPEのみならず,GP等を用いたベイズ最適化のモデルはSMBO(Sequential Model-Based Global Optimization)と呼ばれている.これらの探索手法ではおおまかに以下の図のような流れを取る.

引用元:Algorithms for Hyper-Parameter Optimization
ここで上の変数はそれぞれ以下の通り.
\begin{align}
&\mathcal H:観測点とそれに対応する評価値の集合 \\
&x(\in R^n):ハイパーパラメータベクトル \\
&M_t: イテレーション t 回目時点の目的関数のモデル\\
&f:評価に時間のかかる目的関数(ハイパパラメータと深層学習のLossの関係等)\\
&S:モデルに従って空間上の点がどの程度,Lossを小さくするか予測する関数
\end{align}
SMBOにおいて,アルゴリズムの中枢部分となるのはモデル $M_t$ と候補点の決定であるところのサンプリングと獲得関数の算出方法.以下ではTPEのモデル,獲得関数,候補点のサンプリングについて記述する.
1.モデル
モデルに関する説明はここにも書いてあります.正直,内容はほとんど同じ.
GPではある点における,評価値を横軸に取った確率密度関数(ガウス分布に従うと仮定している)の平均と分散を用いる一方でTPEはある点付近の点が上位群に入る確率密度と下位群に入る確率密度という比較的ざっくりした情報のみを用いる.また,TPEでは各変数の独立性を仮定していることも大きな違いとして上げることができる.(これによりサンプリングは簡単になる.また計算量$\bigl(O(t^3)\rightarrow O(t)\bigl)$の面でも大幅に改善する)
(追記)
変数の独立性の仮定による強さとして,以下のようなものが挙げられる.
・他の変数との相互作用により評価値に影響を与えるが,その変数単独の変化では大きな影響を及ぼさない変数に関して,その変数が当たり障りのなかったときの探索が間接的に記録されるため,結果として変な組み合わせを取らなくなる.(局所探索の原因にもなるかも?)
・単独で強い影響を与える変数の長所を活かしやすい.
以上の議論はLow Effective Dimensionalityとの関連あり.
(1) 観測点を上位群と下位群に分割
$\mathcal H$を上位群 $L=\{X^l_1,X^l_2,...,X^l_{\lceil \gamma t \rceil}\}$ と下位群 $G=\{X^g_1,X^g_2,...,X^g_{t - \lceil \gamma t \rceil}\}$ に分割する(ここでは$X_i=(x^i,f(x^i))$としている.ただし,$i$ は指数でなく通し番号).また,集合内の要素はLossに対して昇順に並んでいる.つまり,良いものから順に並んでいる.
\lceil \gamma t \rceil = \Bigl\lceil min\Bigl( \frac{1}{4}\sqrt{t} , 25 \Bigl) \Bigl\rceil
Optunaのコードだと下のような感じになっています.
def default_gamma(x):
# type: (int) -> int
return min(int(np.ceil(0.25 * np.sqrt(x))), 25)
上位群の集合のサイズが大きくなりすぎないように(経験則的に)制約をかけている.
(2) 上位群と下位群のカーネル密度推定
$l(x), g(x)$ の定義は以下の通り.
\begin{eqnarray}
p(x|y)=\left\{ \begin{array}{ll}
l(x) & (y < y^*) \\
g(x) & (y \geq y^*) \\
\end{array} \right.
\end{eqnarray}
$y$ は損失を表し,$y^{*}$ は上位群と下位群の区切りとなる閾値となる.
あるハイパパラメータの入力 $x$ に対する学習の損失が $y^*$ よりも小さくなる確率密度関数を $l(x)$, 大きくなる確率密度関数を $g(x)$ としている.本来は $y$ が変化するに従って $y$ に基づいた $x$ の確率密度関数も変化するはずですが,ここではざっくり確率密度関数の変化点を閾値 $y^{*}$ の部分に限定している.
最初に $n$ 種類のハイパパラメータ $x=\{x_1,x_2,...,x_n\}$ のそれぞれに対して確率密度関数 $l_i(x_i),g_i(x_i)(i=1,2,...,n)$を求める.確率密度関数の求め方はハイパパラメータの特徴に応じて変わるので以下の表で説明する.
| 変数の種類 | 例 | 分布の推定方法 |
|---|---|---|
| 連続値 | ドロップアウト率等 | カーネル密度推定 |
| 連続値(対数スケール変換) | 学習率,慣性項等 | カーネル密度推定 |
| 離散値 | 層の数,ユニット数等 | カーネル密度推定 |
| カテゴリー | 活性関数の属性等 | 重み付きヒストグラム |
カーネル密度推定に関しては書いている余裕がないので,参考URLに任せます.
・密度関数のカーネル推定量におけるバンド幅の選択について:モンテカルロ実験による小標本特性
・Pythonとカーネル密度推定(KDE)について調べたまとめ
・微分エントロピーのノンパラメトリック推定とその周辺(バンド幅で単語検索)
次にOptunaのアルゴリズムにおけるカーネル密度推定のバンド幅選択について記述する.(参考はoptuna/samplers/tpe/parzen_estimator.py)
カーネル密度推定のハイパパラメータ設定に関して
A.観測点のソート
まず,$x^l=\{x^{l,1},x^{l,2},...,x^{l,m},...\}$ と $x^g=\{x^{g,1},x^{g,2},...,x^{g,m},...\}$ の要素をそれに対応するLossに対して $l$ では昇順に,$g$ では降順に並べる.つまり,
$f(x^{l,1}) \leq f(x^{l,2}) \leq ... \leq f(x^{l,m}) \leq ...$
$f(x^{g,1}) \geq f(x^{g,2}) \geq ... \geq f(x^{g,m}) \geq ...$
となるように並べ替える.
B.カーネル関数の結合係数
次に重みを生成する.
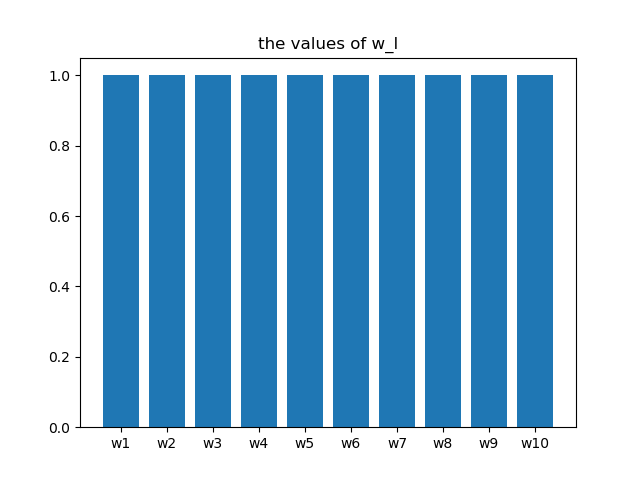
$w^l=\{w^{l,1},w^{l,2},...,w^{l,m},...\}$ と $w^g=\{w^{g,1},w^{g,2},...,w^{g,m},...\}$
ここで,$L$ と $G$ の要素数をそれぞれ $e_{max}^l, e_{max}^g$とすると,
w^{l,m} = 1
\begin{eqnarray}
w^{g,m}=\left\{ \begin{array}{ll}
\frac{e_{max}^g - m}{e_{max}^g - 26} & (if \ m \geq 26) \\
1 & (otherwise) \\
\end{array} \right.
\end{eqnarray}
$w_g$の分布のイメージ(上の式の26を5に変更した際の例)
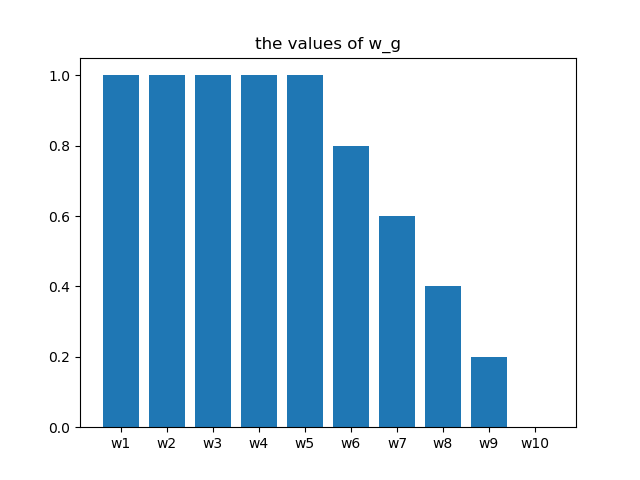
ただし,上の式では $e_{max}^g = 26$ のとき$\frac{(e_{max}^g - 1)}{e_{max}^g(e_{max}^g - 26)}(m - 1) = 0$ としている.
$e_{max}^l$は定義上,25以下であるため,一様に1となっている.一方で,試行を重ねると $e_{max}^g$ は $e_{max}^l$ と比較して大きくなるため,下位群において評価値が良い観測点に関しては線形的に重みの減衰を加えることで閾値による分離精度を上げている(実際にこのアルゴリズムは改良の余地があると思っている).
ここで $w$ の各要素はハイパパラメータの個数 $n$ だけ要素を持つ.したがって, $w^l_i, w^g_i$ をそれぞれ $w^l, w^g$ の各要素の $i$ 番目成分のみを取り出した集合とする.同様に $x^l_i, x^g_i$ をそれぞれ $x^l, x^g$ の各要素の $i$ 番目成分のみを取り出した集合とする.
import numpy as np
wi = np.array([w[j][i] for j in range(len(w))])
xi = np.array([x[j][i] for j in range(len(x))])
$w^l_i, w^g_i$ を $x^l_i, x^g_i$ の要素が昇順に並べたときの順番と同じように並べ替える.
order = np.argsort(xi)
xi_order = xi[order]
wi_order = wi[order]
また,$x_{i,min} \leq x_i \leq x_{i,max}$ として,$\overline x_i=\frac{x_{i,max}+x_{i,min}}{2}$ とする.そのとき,$x_{i,m-1} \leq \overline x_i \leq x_{i,m}$ なる$m$ の位置を $x^l_i, x^g_i$ のそれぞれで求め,その位置に $\overline x_i$ を挿入する.また, $w^l_i, w^g_i$ も $x^l_i, x^g_i$ と対応する位置にそれぞれ重み1を挿入する.その後, $w^l_i, w^g_i$ の各要素をそれぞれの集合の要素の総和で割ることによって,規格化する.
C.各カーネル関数のバンド幅
バンド幅の集合を $\sigma_i$ とすると( $L$ と $G$ で別々に求めるが,ここではアルゴリズムが同じなので添字を省略.また $x$ の要素数を $e_{max}$ とする.),
\begin{eqnarray}
\sigma_{i,m}=\left\{ \begin{array}{ll}
x_{i,1}-x_{i,min} & (if \ m = 1) \\
\max (x_{i,m+1}-x_{i,m}\ ,\ x_{i,m}-x_{i,m-1}) & (if \ 1 < m < e_{max}) \\
x_{i,max}-x_{i,e_{max}} & (if \ m = e_{max}) \\
\end{array} \right.
\end{eqnarray}
これを求めた後,magic_clipという操作を加える.具体的には $\sigma_{i,m}$ の定義域を絞り,定義域を超える値は端点の位置に戻すというものである.
つまり,
sgm_i = np.clip(sgm_i, sgm_i_min, sgm_i_max)
とする.ここで,
\sigma_{i,max} = x_{i,max}-x_{i,min}
\sigma_{i,min} = \frac{\sigma_{i,max}}{\min (1+e_{max}, 100)}
である.
以上に書いたようなバンド幅の選択について,hyperopt/tpe.pyのコメントアウト
A heuristic estimator for the mu and sigma values of a GMM
TODO: try to find this heuristic in the literature, and cite it - Yoshua mentioned the term 'elastic' I think?
実際にhyperoptとOptunaのカーネル密度推定に使われているバンド幅の決定方法はHyperoptの作成者をして"Magic formula"とされている.
(注意)
上での議論は全て各ハイパパラメータの独立性を仮定しているので,
$l(x) = l_1(x_1)\times l_2(x_2)\times ... \times l_n(x_n)$
$g(x) = g_1(x_1)\times g_2(x_2)\times ... \times g_n(x_n)$
となるため,各変数毎の確率密度関数を求めることが意味をなすことに注意.