GridSearchCVはもう古い！Optunaでサポートベクターマシンもラクラクチューニング #Python

chainerでおなじみのPFNがハイパーパラメータ自動最適化ツール「Optuna」を公開したので、これをサポートベクターマシン（回帰）で試してみました。めちゃくちゃ使えますので皆さんもぜひ試してみてください。

Optunaとは

2018/12/3に公開されたPFN製のライブラリ（MITライセンス）。chainerの他にscikit-learn, XGBoost, LightGBMでも使えるのが売り。パラメーターに対して損失なりの評価値を返せればいいので、ここには書いてはいませんがTensorFlowだろうがPyTorchだろうがなんでも使えるはずです。

ハイパーパラメータ自動最適化ツール「Optuna」公開
https://research.preferred.jp/2018/12/optuna-release/

有望そうなハイパーパラメーターを探すのにかなり賢いアルゴリズムを使っているのが特徴で、

Tree-structured Parzen Estimator というベイズ最適化アルゴリズムの一種を用いています

このアルゴリズム自体は全然よくわかりませんが、完全総当たりのGridSearchよりは1万倍ぐらい賢そう。

サポートベクター回帰

サポートベクターマシンの回帰問題のサポートベクター回帰をやってみました。Scikit-learnについてくる、ボストンの住宅価格の予測です。以前GridSearchCVを使っておこなった記事がこちらで、

サポートベクター回帰（SVR）を使ってボストンの住宅価格を予測してみた
https://qiita.com/koshian2/items/baa51826147c3d538652

SVRには主にCとεという2つのハイパーパラメーターがあるのですが¹、GridSearchCVを使って頑張って求めた結果がこちらです。

最適なパラメーター = {'C': 18.329807108324356, 'epsilon': 1.4384498882876631}
交差検証データに対するR2スコア（決定係数） = 0.870461803
テストデータに対するR2スコア（〃） = 0.907877172884

交差検証のR2スコアが0.8705で、テストが0.9079というのを覚えておきましょう。これをOptunaを使ってEnd-to-endで求めてみましょう。

インストール

pipからインストールできます。

pip install optuna

これでもう使えます。簡単ですね。

SVR＋Optuna

以前GridSearchを使って行ったのと全く内容をOptunaで再現してみます。

前処理

まずは前処理です。Train:Validation:Testを6:2:2で分割します。GridSearchだとジェネレーターを作ったり、KFoldのインスタンスを作る必要がありましたが、Optunaではただ単にNumpy配列でおけばOKです。

訓練データを基準に、ValidationとTestを標準化します。

from sklearn.datasets import load_boston
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

import optuna
import numpy as np

boston = load_boston()
X, y = boston["data"], boston["target"]
# 訓練、テスト分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=114514)
n_train = int(X_train.shape[0] * 0.75)
X_train, X_val = X_train[:n_train], X_train[n_train:]
y_train, y_val = y_train[:n_train], y_train[n_train:]

# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_val = scaler.transform(X_val)
X_test = scaler.transform(X_test)

目的関数の作成

Optunaが最適化に使うための関数です。ここではハイパーパラメーターのセットを入力として、最小化する値を出力とする関数を定義します。

# 目的関数
def objective(trial):
    # C
    svr_c = trial.suggest_loguniform('svr_c', 1e0, 1e2)
    # epsilon
    epsilon = trial.suggest_loguniform('epsilon', 1e-1, 1e1)
    # SVR
    svr = SVR(C=svr_c, epsilon=epsilon)
    svr.fit(X_train, y_train)
    # 予測
    y_pred = svr.predict(X_val)
    # CrossvalidationのMSEで比較（最大化がまだサポートされていない）
    return mean_squared_error(y_val, y_pred)

最大化が2018/12/5現在まだサポートされていないので、例えば精度で最適化したかったら、平均2乗誤差を評価に使ったり、1から引いてエラー率としたり工夫してみてください。今回は平均2乗誤差で比較します。

ハイパーパラメータは全てtrialの中に入っているので、ハイパーパラメータの個数が増えたから引数を増やすということは必要ありません。svr_cとepsilonにある、trial.suggest_loguniform('svr_c', 1e0, 1e2)というのは、「svr_cというパラメーターを$10^0=1$～$10^2$の間で対数スケールで調べなさい」という意味です。今ハイパーパラメータの最適解のある場所がだいたい絞られているので、こういう狭い範囲ですが、実践的にはもっと広く見てもいいと思います。これは後で試してみます。

最適化

ものすごい簡単です。optuna.create_study()からoptimize()するだけで簡単に最適化してくれます。これは100回試行する例です。

# optuna
study = optuna.create_study()
study.optimize(objective, n_trials=100)

# 最適解
print(study.best_params)
print(study.best_value)
print(study.best_trial)

最適化の結果は、study.best_params（最適解でのハイパーパラメータの値）、study.best_value（最適解での評価値、この場合はValidationデータの平均2乗誤差）に格納されています。

これを実行すると次のようなメッセージが出てきます。めちゃめちゃ速いです。SVR100回が数秒で終わります。

出力

[I 2018-12-05 19:55:25,166] Finished a trial resulted in value: 7.6590342657643
05. Current best value is 7.509678888529477 with parameters: {'svr_c': 19.04682
554857877, 'epsilon': 1.5323752754042508}.
[I 2018-12-05 19:55:25,197] Finished a trial resulted in value: 7.7412732255113
2. Current best value is 7.509678888529477 with parameters: {'svr_c': 19.046827
54857877, 'epsilon': 1.5323752754042508}.
{'svr_c': 19.046827554857877, 'epsilon': 1.5323752754042508}
7.509678888529477
FrozenTrial(trial_id=62, state=<TrialState.COMPLETE: 1>, value=7.50967888852947
, datetime_start=datetime.datetime(2018, 12, 5, 19, 55, 24, 225021), datetime_c
mplete=datetime.datetime(2018, 12, 5, 19, 55, 24, 243523), params={'svr_c': 19.
46827554857877, 'epsilon': 1.5323752754042508}, user_attrs={}, system_attrs={},
intermediate_values={}, params_in_internal_repr={'svr_c': 19.046827554857877, '
psilon': 1.5323752754042508})

Optunaが最適なハイパーパラメータを求めてくれました。

'svr_c': 19.46827554857877, 'epsilon': 1.5323752754042508

だそうです。これをメモしておきます。ちなみにGridSearchを使って計算した場合は、C=18.3, ε=1.44だったのでだいたい同じです。

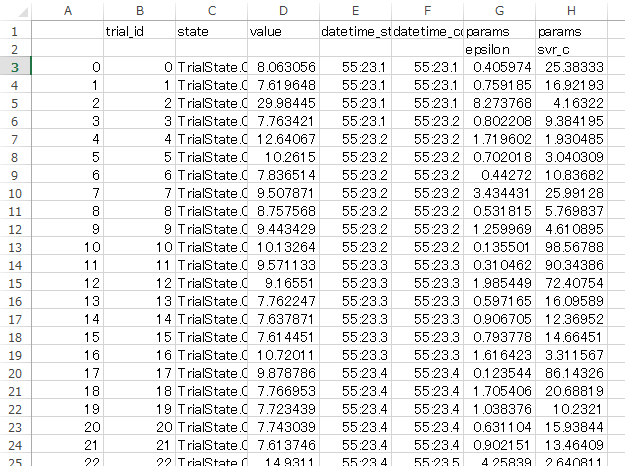
ちなみに試行結果はSQLiteで保存されていますが、PandasのDataFrameに書き出すこともできます。これはstudy.trials_dataframe()でできます。CSVに書き出したいときは、DataFrameを経由するのが簡単ですね。

# history
hist_df = study.trials_dataframe()
hist_df.to_csv("boston_svr.csv")

評価

では早速テストデータに対してどれぐらいの精度（R2スコア）を出すのか評価してみましょう。

普通のSVRのコードで、先程のOptunaが求めてくれたハイパーパラメータをコピペしただけです。

from sklearn.datasets import load_boston
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score

import numpy as np

boston = load_boston()
X, y = boston["data"], boston["target"]
# 訓練、テスト分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=114514)
n_train = int(X_train.shape[0] * 0.75)
X_train, X_val = X_train[:n_train], X_train[n_train:]
y_train, y_val = y_train[:n_train], y_train[n_train:]

# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_val = scaler.transform(X_val)
X_test = scaler.transform(X_test)

# SVR
svr = SVR(C=19.046827554857877, epsilon=1.5323752754042508)
svr.fit(X_train, y_train)
y_pred_val = svr.predict(X_val)
y_pred_test = svr.predict(X_test)

val_r2 = r2_score(y_val, y_pred_val)
test_r2 = r2_score(y_test, y_pred_test)
print("交差検証データ　R2 : ", val_r2)
print("テストデータ　R2 : ", test_r2)

結果は次のようになります。

出力

交差検証データ　R2 :  0.8685237976554909
テストデータ　R2 :  0.9081066406039279

ちなみにGridSearchを使って頑張って求めたケースでは、交差検証のR2スコアが0.8705で、テストが0.9079だったので、Optunaでは（高速かつEnd-to-Endに）ほぼそれと遜色ないぐらいの精度は出せるということがわかります。テスト精度はわずかにOptunaのほうが良いですね。

試行履歴を見てみる

csvに出力した履歴を見てみます。

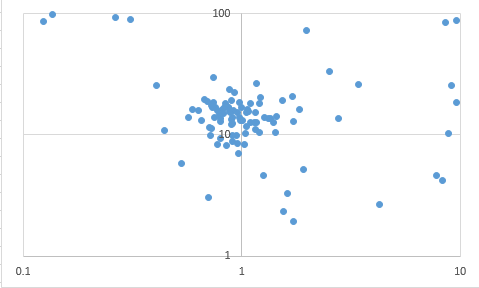
とてもわかりやすいです。εとCの履歴もあるので、どのへんを狙ってハイパーパラメータを探しているか散布図に書いてみました。

横軸がεで、縦軸がCです。対数スケールで探しているので対数プロットをしてみました。なるほど、最適解がありそうなスイートスポットを集中的に狙っているのがわかります。これは総当たりのGridSearchよりかは遥かに賢そうなアルゴリズムですね。

もっと広い範囲で調べてみる

実際の問題ではハイパーパラメータがどこらへんにあるかというのはよくわからないので、Cもεも$10^{-10}$～$10^{10}$まで調べてみました。それでもかなり最適解に近い値は返してくれました。

{'svr_c': 14.312804360445284, 'epsilon': 7.474784105854122e-09}
7.921504496284093

GridSearch同様、大まかに最適解の範囲を絞って、範囲を狭くしてもう一度やってみるみたいな使い方もありではないでしょうか。慣れればGridSearchと似たような感覚で使えます。

本命は勾配ブースティング？

Optunaをディープラーニングで使おうとすると、並列化して大量のモデルを同時に訓練できるだけの計算リソースがないと厳しいので、一般人がなかなか恩恵に預かるというのは厳しいと思います。しかし、これはGridSearchの代用品として使えるので、Optunaの本命はXGBoostやLightGBMといった勾配ブースティングではないかと自分は思います。これらのアルゴリズムはディープラーニングに対抗できるぐらいの精度が出せることは、Kaggleを見れば保証できます。勾配ブースティングの計算量はディープラーニングよりはまだ軽いです。

もちろん、今回見たようにサポートベクターマシンでも無双すると思います。また、サンプルやドキュメントを見ると書いてあるのですが、要はインプット（ハイパーパラメータが入っている試行の引数）に対して、何らかの評価尺度を返す目的関数を作ればあとはいい感じに最適化してくれるので、例えば「SVMとランダムフォレスト、勾配ブースティングを同時に試行する」ということができます。これはコンペの強い味方ではないでしょうか。

公式のGitHubのほうにXGBoostやLightGBMの例などもあるので、興味があったらぜひのぞいてみてください。これはPFN、「Great job!」ではないでしょうか。

追記

ナップサック問題についてOptunaで解いてみたら、必ずしも最適解には行かないみたいです。あからさまな局所解がある設定だと、局所解にハマってしまうというような状況もありました。ただ、推移のプロットを見ている限り、ある程度の局所解に対するロバスト性はあるのではないかと思います（必ず大域最適解に行くのが保証できないだけです）。

環境：Optuna　0.4.0

問題設定
500円玉、100円玉、50円玉、10円玉、5円玉、1円玉を最大で合計7枚まで使い、2019円に最も近づける組み合わせはどれか。ただし、2019円を超えてはいけない。

これの最適解は、500円玉×4＋10円玉×1＋5円玉×1＋1円玉×1＝2016円です。

これはちゃんとしたアルゴリズムで書けば解けるのですが、楽したかったのでグリーディーな設定にして全部Optunaにまかせてしまいました。ちゃんと書けば解いてくれると思います。

import optuna
import numpy as np

# 硬貨7枚以内で2019円に近づける
def knapsack(trial):
    coin500 = trial.suggest_int('coin500', 0, 7)
    coin100 = trial.suggest_int('coin100', 0, 7)
    coin50 = trial.suggest_int('coin50', 0, 7)
    coin10 = trial.suggest_int('coin10', 0, 7)
    coin5 = trial.suggest_int('coin5', 0, 7)
    coin1 = trial.suggest_int('coin1', 0, 7)

    # 枚数
    coin_num = coin500 + coin100 + coin50 + coin10 + coin5 + coin1
    # 値段
    coin_price = coin500*500 + coin100*100 + coin50*50 + coin10*10 + coin5*5 + coin1

    # 損失関数
    if coin_price <= 2019 and coin_num <= 7:
        loss = 2019 - coin_price
    else:
        loss = 100000000 + np.abs(2019-coin_price) + (coin_num - 7) # 十分大きな値
        # loss = (2019-coin_price+5)**2 + ((coin_num - 7)*100)**2　←これでもうまくいかない

    return loss

def main():
    study = optuna.create_study()
    study.optimize(knapsack, n_trials=1000)
    print(study.best_params)
    print(study.best_value)

    study_df = study.trials_dataframe()
    study_df.to_csv("knapsack.csv")

if __name__ == "__main__":
    main()

上の損失関数で解くと、500円玉×4＋5円玉×3の組み合わせにハマって、5円玉を0枚、1枚の組み合わせを全然試してくれませんでした。

下の損失関数で解くと、7枚をオーバーするケースが出てあまり効率よくなかったです。最も良いと記されたのは「500円玉×4＋10円玉×1＋1円玉×2」でした。

したがって、場合によってはランダムサーチや、人間の手によってヒューリスティックにチューニングしたほうがいい結果が出るかもしれません。あくまで可能性の範囲なので、どこまでOptunaが勝るかはこれから次第だと思います。

より正確にいうと、Cとεとγの3つです。ただし、γについてはSklearnのSVRがいい感じに置いてくれるという、ありがたいオプションがデフォルトでついているので、実質2つで考えることができます。 ↩