機械学習勉強中です。サポートベクターマシン(SVM)について調べていたら、この派生版でサポートベクター回帰(SVR)というのがあるのを知りました。理論的なことは以下参照。
参考:サポートベクター回帰(Support Vector Regression, SVR)~サンプル数10000以下ならこれを使うべし!~
参考:サポート ベクター マシン回帰について
このサポートベクター回帰(SVR)を使って、回帰分析でよく使うボストンデータの土地価格を分析してみました。流れとしては、(1)重回帰分析(リッジ回帰)→(2)カーネルなしSVR→(3)ガウシアンカーネルのSVRで順に分析し、予測精度(決定係数)を比較してみます。このデータの詳細は以下参照。
Qiita内関連記事:
1.重回帰分析(リッジ回帰)
まずは(いつもの)重回帰分析でどの程度精度が出るか見てみます。変数は特に削らずに、標準化したものを全て使います。正則化も行うためリッジ回帰を使います。
したがって、交差検証で最適化するハイパーパラメータは、正則化のα1つだけです。(重回帰自体が正規方程式で解けるし、ハイパーパラメータが少ないからむちゃくちゃ計算が速い)
まずはデータを読み込みます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
# データの読み込み
boston = load_boston()
# 訓練データ、テストデータに分割
X, Xtest, y, ytest = train_test_split(boston['data'], boston['target'], test_size=0.2, random_state=114514)
# 6:2:2に分割にするため、訓練データのうちの後ろ1/4を交差検証データとする
# 交差検証データのジェネレーター
def gen_cv():
m_train = np.floor(len(y)*0.75).astype(int)#このキャストをintにしないと後にハマる
train_indices = np.arange(m_train)
test_indices = np.arange(m_train, len(y))
yield (train_indices, test_indices)
# (それぞれ303 101 102 = サンプル合計は506)
print("リッジ回帰")
print()
print("訓練データ、交差検証データ、テストデータの数 = ", end="")
print(len(next(gen_cv())[0]), len(next(gen_cv())[1]), len(ytest) )
print()
6:2:2で訓練データ、交差検証データ、テストデータに分割します。train_test_splitで行っているのでシャッフルが入ります。Scikit-learnでの実装上は、訓練データと交差検証データを分ける必要はないので、インデックスだけ分けて進めます。
訓練データ、交差検証データ、テストデータの数 = 303 101 102
SVRでは標準化が重要になるので、ここで標準化しておきます。StandardScalerで「(X-平均)/標準偏差」の標準化をします。
# 訓練データを基準に標準化(平均、標準偏差で標準化)
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)
# テストデータも標準化
Xtest_norm = scaler.transform(Xtest)
ここでポイントなのが、訓練データの平均分散を基準にして、テストデータを標準化すること。厳密にやるなら平均分散計算時に交差検証データを一旦除外したほうがいいかもしれません。fitが入ると平均分散がアップデートされてるので、訓練データはfit_transform、テストデータはtransformで計算します。【ここから分岐】
次に正則化のハイパーパラメータαをチューニングします。Scikit-learn組み込みのGridSearchCVを使うと便利です。
# ハイパーパラメータのチューニング
params = {"alpha":np.logspace(-2, 4, 24)}
gridsearch = GridSearchCV(Ridge(), params, cv=gen_cv(), scoring="r2", return_train_score=True)
gridsearch.fit(X_norm, y)
print("αのチューニング")
print("最適なパラメーター =", gridsearch.best_params_, "精度 =", gridsearch.best_score_)
print()
αのチューニング
最適なパラメーター = {'alpha': 149.24955450518291} 精度 = 0.6901305867
検証曲線(Validation curve)を描いてみると次のようになります。
# 検証曲線
plt.semilogx(params["alpha"], gridsearch.cv_results_["mean_train_score"], label="Training")
plt.semilogx(params["alpha"], gridsearch.cv_results_["mean_test_score"], label="Cross Validation")
plt.xlabel("alpha")
plt.ylabel("R2 Score")
plt.title("Validation curve / Linear Regression")
plt.legend()
plt.show()
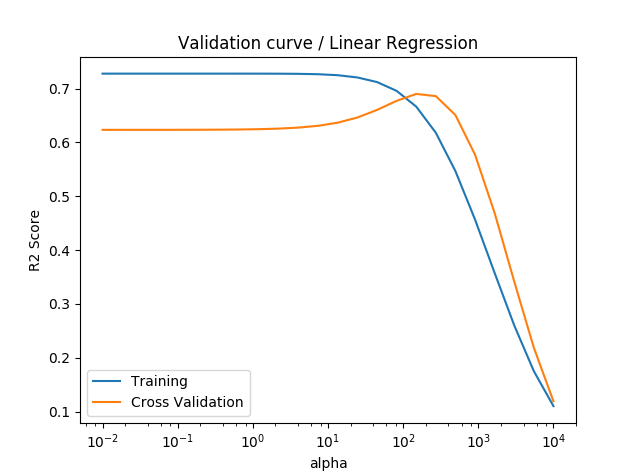
αが10^2ちょい(149)でCVの精度(決定係数)が最大化されることがわかりました。コンソールに出ているgridsearch.best_score_は交差検証データに対する決定係数です。
このαを代入し、テストデータに対する精度を求めます。
# チューニングしたαでフィット
regr = Ridge(alpha=gridsearch.best_params_["alpha"])
train_indices = next(gen_cv())[0]
valid_indices = next(gen_cv())[1]
regr.fit(X_norm[train_indices, :], y[train_indices])
print("切片と係数")
print(regr.intercept_)
print(regr.coef_)
print()
# テストデータの精度を計算
print("テストデータにフィット")
print("テストデータの精度 =", regr.score(Xtest_norm, ytest))
print()
print("※参考")
print("訓練データの精度 =", regr.score(X_norm[train_indices, :], y[train_indices]))
print("交差検証データの精度 =", regr.score(X_norm[valid_indices, :], y[valid_indices]))
重回帰分析(リッジ回帰)の場合、テストデータに対する決定係数は0.771となりました。交差検証データの精度のところにある数字が、αを最適化したときの最良の精度と一致していることが確認できます。
切片と係数
22.894475515
[-0.46859903 0.51250995 -0.3442444 0.94872076 -0.55979359 2.44809376
-0.08501653 -1.08998267 0.48920143 -0.35536464 -1.38784054 0.60839819
-2.86193018]
テストデータにフィット
テストデータの精度 = 0.771351835238
※参考
訓練データの精度 = 0.666603023327
交差検証データの精度 = 0.6901305867
2.カーネルなし(線形カーネル)のサポートベクター回帰(SVR)
次はカーネルなし(線形カーネル)のサポートベクター回帰を実行します。
リッジ回帰における標準化までの処理は共通なので、リッジ回帰の【ここから分岐】と書いたところまでは省略します。標準化が終わり、ハイパーパラメーターの最適化のところからです。
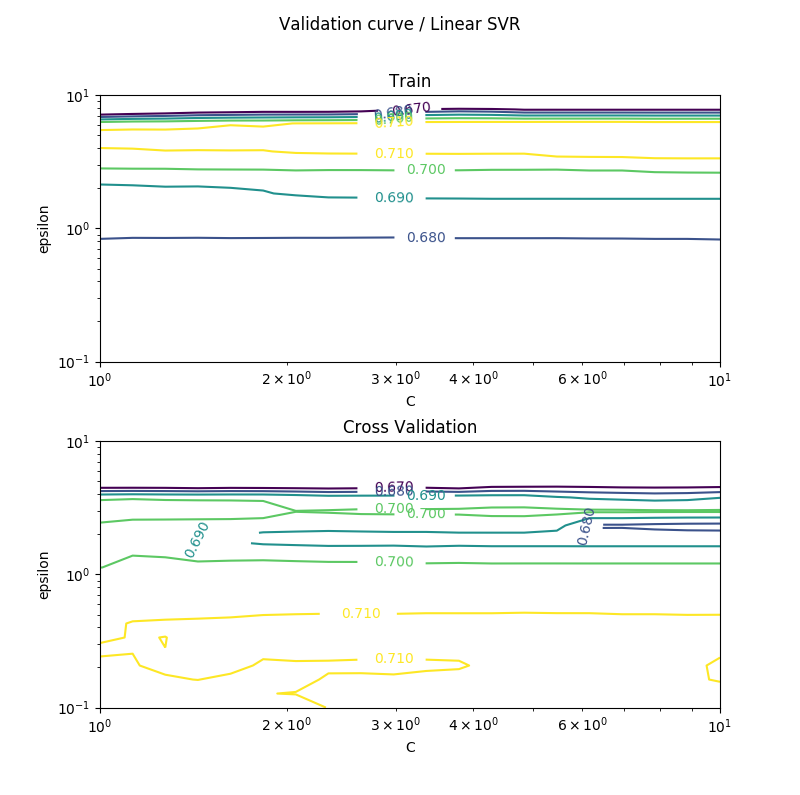
分類問題で使うサポートベクターマシン(SVM)では、カーネルなしなら、ハイパーパラメーターは正則化のCだけでOKでした。一方で回帰問題で使うサポートベクター回帰(SVR)では、線形カーネルでも正則化のCのほかにεという(誤差のチューブというそうです)ハイパーパラメーターが必要になります。したがって2次元のハイパーパラメーターの最適化を行う必要があります。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
# ハイパーパラメータのチューニング
# 計算に時間がかかるのである程度パラメーターを絞っておいた
# (1e-2~1e4まで12×12でやって最適値が'C': 0.123, 'epsilon': 1.520)
params_cnt = 20
params = {"C":np.logspace(0,1,params_cnt), "epsilon":np.logspace(-1,1,params_cnt)}
gridsearch = GridSearchCV(SVR(kernel="linear"), params, cv=gen_cv(), scoring="r2", return_train_score=True)
gridsearch.fit(X_norm, y)
print("C, εのチューニング")
print("最適なパラメーター =", gridsearch.best_params_)
print("精度 =", gridsearch.best_score_)
print()
グリッドサーチ(総当たり)で試すと次元数のべき乗で試行回数が増えていく(今回は2乗)ので、予め大きめの区切りで調べてから解がどのへんにあるか見当をつけてから、細かい区切りで調べていったほうが効率よさそうです。
C, εのチューニング
最適なパラメーター = {'C': 5.4555947811685188, 'epsilon': 0.42813323987193935}
精度 = 0.715406026365
若干重回帰分析と比べて上がっているものの、あまり差がないように思えます。検証曲線(3次元グラフなので曲面ですが)を描いてみます。グラフの形に迷いましたが、等高線グラフが一番わかりやすかったです。
黄色いエリアが相関の高い区域です。最適化したハイパーパラメーターを戻してフィットさせます。
# チューニングしたハイパーパラメーターをフィット
regr = SVR(kernel="linear", C=gridsearch.best_params_["C"], epsilon=gridsearch.best_params_["epsilon"])
train_indices = next(gen_cv())[0]
valid_indices = next(gen_cv())[1]
regr.fit(X_norm[train_indices, :], y[train_indices])
print("切片と係数")
print(regr.intercept_)
print(regr.coef_)
print()
# テストデータの精度を計算
print("テストデータにフィット")
print("テストデータの精度 =", regr.score(Xtest_norm, ytest))
print()
print("※参考")
print("訓練データの精度 =", regr.score(X_norm[train_indices, :], y[train_indices]))
print("交差検証データの精度 =", regr.score(X_norm[valid_indices, :], y[valid_indices]))
切片と係数は重回帰と似たり寄ったりな感じです。なので、カーネルなしSVRは重回帰にちょっと毛が生えた程度です。カーネルなし(線形カーネル)のSVRでは、テストデータに対する決定係数は0.834となりました。訓練、交差検証、テストのどのデータに対しても重回帰よりは若干決定係数が上がっていることが確認できます。
切片と係数
[ 21.81797651]
[[-0.92484711 0.86695412 0.21481883 0.41999003 -1.09412238 3.61505818
-0.57109515 -1.88140038 1.72847067 -1.61440302 -1.76307077 0.72193288
-2.69598779]]
テストデータにフィット
テストデータの精度 = 0.834020950565
※参考
訓練データの精度 = 0.675689363164
交差検証データの精度 = 0.715406026365
3.ガウシアンカーネルのサポートベクター回帰(SVR)
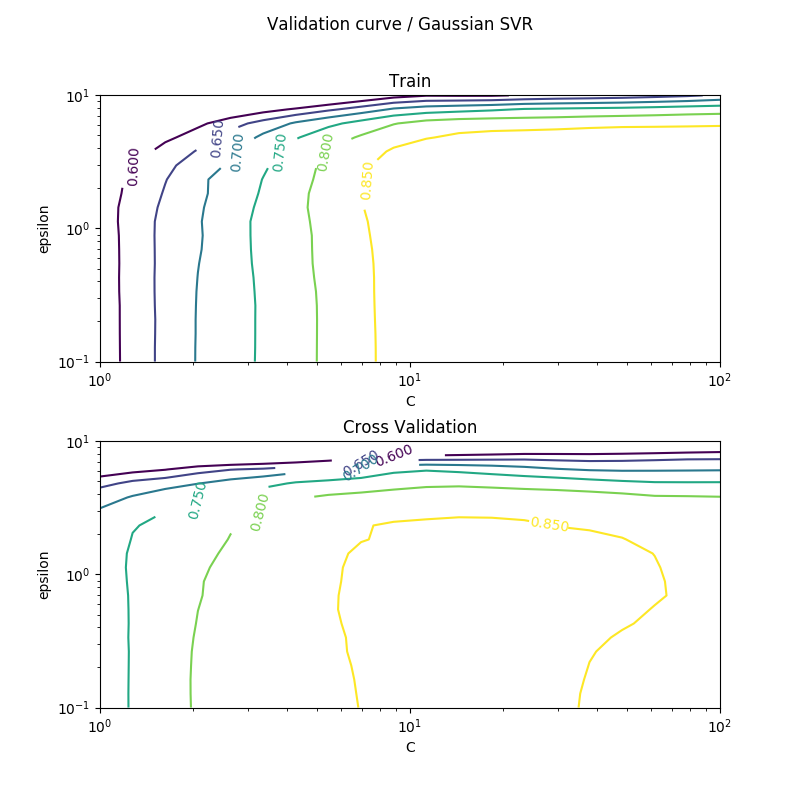
今度はガウシアンカーネルを使ったサポートベクター回帰(SVR)で予測をします。サポートベクターマシン(SVM)のガウシアンカーネルを使った場合のハイパーパラメーターは、正則化のCとγでしたが、サポートベクター回帰の場合は誤差のεを含めて3つになります。
ただし、ここでは計算の簡略化のために、似たような意味合いを持つCとγのうち、γを固定しました。Scikit-learnでもデフォルトでγを指定しなければ、オートとしてγ=1/変数の数と計算します。ライブラリ側から「Cとγが似たようなパラメーターだから、Cだけ調整すればだいたいよくね?」というありがたい提案かもしれません。これはSVM/SVR問わずそうです。
もちろんγもちゃんと計算したほうが精度はより良くなるはずですが、グリッドサーチの量が2乗から3乗はちょっとなーと。そのためここではγをデフォルトの「auto」としています。(ちなみにSVM/SVRのハイパーパラメーターの計算量の問題は、解決法があるそうです。後ほど書きます。)
ほぼ、カーネルなしのSVRのときと変わらない(SVRの引数のkernelが変わっただけ)ですが、楽にコピペできるように全てのコードを書いておきます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
# データの読み込み
boston = load_boston()
# 訓練データ、テストデータに分割
X, Xtest, y, ytest = train_test_split(boston['data'], boston['target'], test_size=0.2, random_state=114514)
# 6:2:2に分割にするため、訓練データのうちの後ろ1/4を交差検証データとする
# 交差検証データのジェネレーター
def gen_cv():
m_train = np.floor(len(y)*0.75).astype(int)#このキャストをintにしないと後にハマる
train_indices = np.arange(m_train)
test_indices = np.arange(m_train, len(y))
yield (train_indices, test_indices)
# (それぞれ303 101 102 = サンプル合計は506)
print("ガウシアンカーネルのSVR")
print()
# 訓練データを基準に標準化(平均、標準偏差で標準化)
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)
# テストデータも標準化
Xtest_norm = scaler.transform(Xtest)
# ハイパーパラメータのチューニング
params_cnt = 20
params = {"C":np.logspace(0,2,params_cnt), "epsilon":np.logspace(-1,1,params_cnt)}
gridsearch = GridSearchCV(SVR(), params, cv=gen_cv(), scoring="r2", return_train_score=True)
gridsearch.fit(X_norm, y)
print("C, εのチューニング")
print("最適なパラメーター =", gridsearch.best_params_)
print("精度 =", gridsearch.best_score_)
print()
# 検証曲線
plt_x, plt_y = np.meshgrid(params["C"], params["epsilon"])
fig = plt.figure(figsize=(8,8))
fig.subplots_adjust(hspace = 0.3)
for i in range(2):
if i==0:
plt_z = np.array(gridsearch.cv_results_["mean_train_score"]).reshape(params_cnt, params_cnt, order="F")
title = "Train"
else:
plt_z = np.array(gridsearch.cv_results_["mean_test_score"]).reshape(params_cnt, params_cnt, order="F")
title = "Cross Validation"
ax = fig.add_subplot(2, 1, i+1)
CS = ax.contour(plt_x, plt_y, plt_z, levels=[0.6, 0.65, 0.7, 0.75, 0.8, 0.85])
ax.clabel(CS, CS.levels, inline=True)
ax.set_xscale("log")
ax.set_yscale("log")
ax.set_xlabel("C")
ax.set_ylabel("epsilon")
ax.set_title(title)
plt.suptitle("Validation curve / Gaussian SVR")
plt.show()
# チューニングしたC,εでフィット
regr = SVR(C=gridsearch.best_params_["C"], epsilon=gridsearch.best_params_["epsilon"])
train_indices = next(gen_cv())[0]
valid_indices = next(gen_cv())[1]
regr.fit(X_norm[train_indices, :], y[train_indices])
# テストデータの精度を計算
print("テストデータにフィット")
print("テストデータの精度 =", regr.score(Xtest_norm, ytest))
print()
print("※参考")
print("訓練データの精度 =", regr.score(X_norm[train_indices, :], y[train_indices]))
print("交差検証データの精度 =", regr.score(X_norm[valid_indices, :], y[valid_indices]))
ハイパーパラメーターの最適化。カーネルなしの場合より明らかに精度上がっています。
ガウシアンカーネルのSVR
C, εのチューニング
最適なパラメーター = {'C': 18.329807108324356, 'epsilon': 1.4384498882876631}
精度 = 0.870461802925
テストデータにフィットさせると以下の通り。
テストデータにフィット
テストデータの精度 = 0.907877172884
※参考
訓練データの精度 = 0.91960213998
交差検証データの精度 = 0.870461802925
ガウシアンカーネルによるSVRの場合は、テストデータに対する決定係数が0.907と0.9を越えました。この決定係数が重回帰の場合は0.77、カーネルなしSVRの場合は0.83であったことを思い出すと、相当良くなっています。
とりあえず手軽に精度がほしい場合はSVRに任せれば良さそうですね。
余談:SVM/SVRのハイパーパラメーターの効率的な探し方
冒頭のSVRの記事を見ていたら興味深いものを見つけました。
[Pythonコードあり] サポートベクター回帰(Support Vector Regression, SVR)のハイパーパラメータを高速に最適化する方法
ここではC,γ、εの3つを最適化することを考えます。
- 「yの平均±標準偏差×3」の絶対値のうち大きい方(yが標準化されていれば3)をCの初期値とする
- 1の初期値をもとにγをグラム行列の分散を最大化するようなγを選ぶ。Cとγを固定して、εだけの1次元の最適化を行う
- 2で求めたε、グラム行列の分散が最大となるγで固定して、Cだけの1次元の最適化を行う
- 最後にγの最適化をする。3で求めたC、2で求めたεをもとに、γだけの1次元の最適化を行う
- これでC、γ、εの最適値が求まる
グラム行列の分散の最大化というイメージが湧きづらいですが、上記の記事を書いている先生(明治大学の先生)が公開しているコードによると、こうなるそうです。
# Optimize gamma by maximizing variance in Gram matrix
numpyautoscaledXtrain = np.array(autoscaledXtrain)
varianceofgrammatrix = list()
for svrgamma in svrgammas:
grammatrix = np.exp(-svrgamma*((numpyautoscaledXtrain[:, np.newaxis] - numpyautoscaledXtrain)**2).sum(axis=2))
varianceofgrammatrix.append(grammatrix.var(ddof=1))
optimalsvrgamma = svrgammas[ np.where( varianceofgrammatrix == np.max(varianceofgrammatrix)
ここからは自分の雑感ですが、これはSVM/SVRの誤差関数が凸関数だからという性質によるものが大きいと思います。SVMが凸最適化であることはよく知られていますが、SVRの場合も「Support vector regression convex」で検索すると『Convex Cost Functions for Support Vector Regression』のような論文が出てくるので、凸最適化であると考えてよいと思います。
凸関数なら極小値は存在せず収束した場所=大域的最適解なので、パラメーターを固定しながら動かしても(局所的な最適化をしても)、結局は最適解にたどり着くであろうと、すごいアバウトですが理解しました。もしニューラルネットワークのように、非凸最適化だったらこのようなことはできないと思います。
C、γ、εの探索する数が全て$N$であったとすると、グリッドサーチで貪欲に求める場合の計算量は$O(N^3)$となりますが、この方法を使えば$O(3N)=O(N)$となるはずです。アルゴリズム的にはとても優秀です。
まとめ
以上、ボストンの住宅価格データを(1)重回帰分析、(2)カーネルなしSVR、(3)ガウシアンカーネルのSVRを使って分析しました。結果をまとめます。
| モデル | ハイパーパラメーターの数 | テストデータの決定係数(R2) | 訓練データR2 | 交差検証データR2 |
|---|---|---|---|---|
| 重回帰分析(リッジ回帰) | 1 | 0.771351835 | 0.666603023 | 0.690130587 |
| カーネルなしSVR | 2 | 0.834020951 | 0.675689363 | 0.715406026 |
| ガウシアンカーネルのSVR | 3[*] | 0.907877173 | 0.91960214 | 0.870461803 |
[*] 本来、ハイパーパラメーターの数は3だが、今回はγをauto(1/変数の数)として固定し、実質2つのハイパーパラメーターとして最適化
カーネルなしのSVRのテストデータに対する決定係数は高めですが、訓練データと交差検証データの決定係数があまり高くないので、この0.83はあまり信用できなさそうな感じはします。カーネル入れなかったら重回帰に毛が生えた程度ぐらいと思っておいたほうが良さそうです。
こうして見ると、ガウシアンカーネルのSVRはかなり優秀ですね。どの集合に対しても9割近い決定係数を出しているので、テストデータに対する0.907という値も信用できるものでしょう。どのモデルでも変数の取捨選択をせずに、標準化して丸ごと放り込みましたが、こんな雑な処理で9割出るのはびっくりしました。
SVCと同じ感覚で回帰問題にも使えるSVR、かなりお世話になるのではないでしょうか。