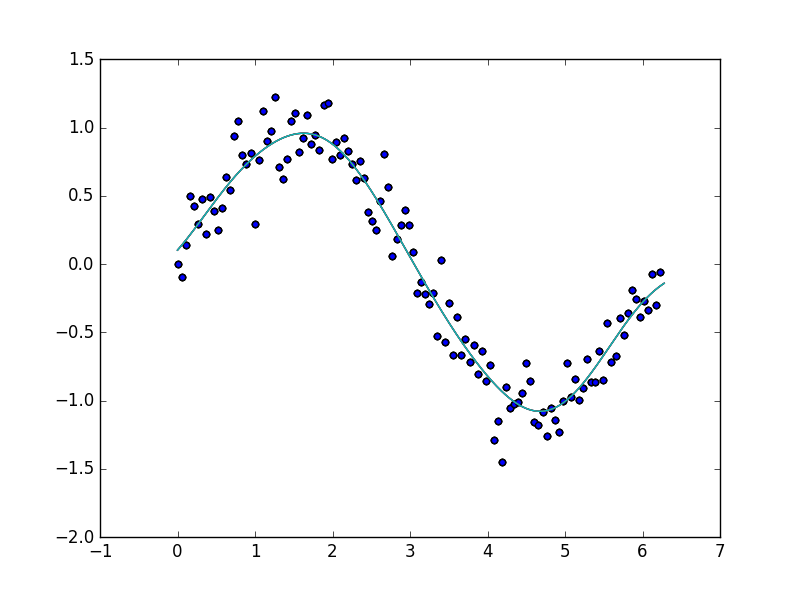
サポートベクトル回帰
サポートベクトル回帰は機械学習手法の1つで、関数形を仮定しなくても回帰曲線を推定してくれるので多変量の非線形回帰問題に適しています。また共線性に強く、とりあえず説明変数を使えるだけ突っ込むような乱暴な使い方をしても不安定になりづらいという特長があります。
import numpy as np
import random
import matplotlib.pyplot as plt
from sklearn import svm
PI = 3.14
# 0~2πまでを120等分した点を作る
X = np.array(range(120))
X = X * 6 * PI / 360
# y=sinXを計算し、ガウス分布に従う誤差を加える
y = np.sin(X)
e = [random.gauss(0, 0.2) for i in range(len(y))]
y += e
# 列ベクトルに変換する
X = X[:, np.newaxis]
# 学習を行う
svr = svm.SVR(kernel='rbf')
svr.fit(X, y)
# 回帰曲線を描く
X_plot = np.linspace(0, 2*PI, 10000)
y_plot = svr.predict(X_plot[:, np.newaxis])
# グラフにプロットする。
plt.scatter(X, y)
plt.plot(X_plot, y_plot)
plt.show()
特徴選択の問題
一般的にはサポートベクトル回帰の回帰曲線は高次元の特徴空間への非線形写像となっています。そのため、重回帰分析などのように単純に係数の絶対値から各説明変数の説明力への寄与を推測するようなことができません。(できないよね?)
そこで、感度分析を行って感度の小さい変数から順に削除しながら決定係数の推移を記録しておき、決定係数が大きく低下する直前の変数セットを有効な特徴として用いるという手段が有効と考えられます。
手法と実装
この文献を参考にしました。
決定係数の評価
- 全ての特徴量を使って回帰曲線を求め、決定係数を計算します(グリッドサーチ+クロスバリデーションをしておくことを推奨します)
感度分析
- 学習データとテストデータに分割します。テストデータについては、感度を求めたい変数以外の変数の値をその変数の平均値に置換しておきます。
- 学習データを用いて学習し、2で作ったテストデータからの出力値を求めます。
- 感度を求めたい変数を説明変数、出力値を目的変数とする単回帰分析を行い、その傾きの絶対値を感度とします。
特徴選択
- すべての特徴について決定係数の評価と感度分析を行ったら、感度が最小の特徴を削除します。
- これを1ラウンドとし、上記のプロセスを繰り返します。
- 特徴を削減する過程での決定係数の推移を確認して、好きなところまで変数を削りましょう。
テスト
scikit-learnに備え付けの、ボストンの住宅価格のデータを使って検証してみます。
特徴削減のラウンド数と決定係数
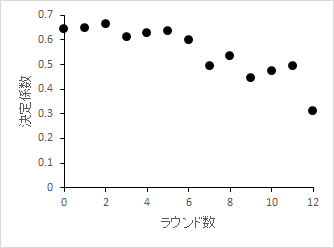
いくつかの特徴量を削っても決定係数が急激には落ち込まないことがわかります。
表にすると以下のようになります。
| ラウンド数 | 除かれた特徴量 | 決定係数 |
|---|---|---|
| 0 | - | 0.644 |
| 1 | ZN | 0.649 |
| 2 | INDUS | 0.663 |
| 3 | CHAS | 0.613 |
| 4 | CRIM | 0.629 |
| 5 | RAD | 0.637 |
| 6 | NOX | 0.597 |
| 7 | PTRATIO | 0.492 |
| 8 | B | 0.533 |
| 9 | TAX | 0.445 |
| 10 | DIS | 0.472 |
| 11 | AGE | 0.493 |
| 12 | RM | 0.311 |
| 最後に残った特徴量はLSTATです。 |
各特徴量の意味は大雑把には以下の通りです。詳しくはここを参照。
CRIM: 一人あたり犯罪発生率
ZN: 25000平方フィート以上の宅地割合
INDUS: 小売業以外の業種の割合
CHAS: チャールズ川に接しているかどうか
NOX: 窒素酸化物濃度
RM: 部屋数
AGE: 1940年以前に建築された持家の割合
DIS: Boston employment centresへの距離
RAD: 放射状高速道路へのアクセスしやすさ
TAX: 満期固定資産税率
PTRATIO: 教師一人あたりの生徒数
B: 人口に対する黒人数の割合
LSTAT: 下層民の割合
この結果から以下のようなことがわかります。
-
NOX,PTRATIO,B,TAX,DIS,AGE,RM,LSTATの上位8つの特徴量だけでも全特徴量を使った場合と遜色ない推定能力がある。
-
ボストンの住宅価格を予想するにはZNやINDUSよりもLSTATやRMが重要。
このように感度分析を組み合わせることで、サポートベクトル回帰を用いた場合にも特徴量の寄与度をランク付けできます。
最後に特徴選定に用いたコードを記載しておきます。
def standardize(data_table):
for column in data_table.columns:
if column in ["target"]:
continue
if data_table[column].std() == 0:
data_table.loc[:, column] = 0
else:
data_table.loc[:, column] = ((data_table.loc[:,column] - data_table[column].mean())
/ data_table[column].std())
return data_table
# 感度の計算を行うメソッドです
def calculate_sensitivity(data_frame, feature_name, k=10):
import numpy as np
import pandas as pd
from sklearn import svm
from sklearn import linear_model
from sklearn import grid_search
# グリッドサーチ用のパラメータを設定します
tuned_parameters = [{'kernel': ['rbf'], 'gamma': [10**i for i in range(-4, 0)],
'C': [10**i for i in range(1,4)]}]
# 傾きの値を格納するリストです。
slope_list = []
# サンプルサイズ
sample_size = len(data_frame.index)
features = list(data_frame.columns)
features.remove("target")
for number_set in range(k):
# データを学習用とテスト用に分割します。
if number_set < k - 1:
test_data = data_frame.iloc[number_set*sample_size//k:(number_set+1)*sample_size//k,:]
learn_data = pd.concat([data_frame.iloc[0:number_set*sample_size//k, :],data_frame.loc[(number_set+1)*sample_size//k:, :]])
else:
test_data = data_frame[(k-1)*sample_size//k:]
learn_data = data_frame[:(k-1)*sample_size//k]
# それぞれをラベルと特徴量に分割します
learn_label_data = learn_data["target"]
learn_feature_data = learn_data.loc[:,features]
test_label_data = test_data["target"]
test_feature_data = test_data.loc[:, features]
# テストデータの感度分析を行う対象以外の列を、列平均で置換します。
for column in test_feature_data.columns:
if column == feature_name:
continue
test_feature_data.loc[:, column] = test_feature_data[column].mean()
# SVRのために、それぞれのデータをnumpy.array形式に変換します。
X_test = np.array(test_feature_data)
X_linear_test = np.array(test_feature_data[feature_name])
X_linear_test = X_linear_test[:, np.newaxis]
y_test = np.array(test_label_data)
X_learn = np.array(learn_feature_data)
y_learn = np.array(learn_label_data)
# 回帰分析を行い、出力を得ます
gsvr = grid_search.GridSearchCV(svm.SVR(), tuned_parameters, cv=5, scoring="mean_squared_error")
gsvr.fit(X_learn, y_learn)
y_predicted = gsvr.predict(X_test)
# 出力に対する線形回帰を行います。
lm = linear_model.LinearRegression()
lm.fit(X_linear_test, y_predicted)
# 傾きを取得します
slope_list.append(lm.coef_[0])
return np.array(slope_list).mean()
# 決定係数の計算を行うメソッドです。
def calculate_R2(data_frame,k=10):
import numpy as np
import pandas as pd
from sklearn import svm
from sklearn import grid_search
# グリッドサーチ用のパラメータを設定します
tuned_parameters = [{'kernel': ['rbf'], 'gamma': [10**i for i in range(-4, 0)],
'C': [10**i for i in range(1,4)]}]
svr = svm.SVR()
# 各回の決定係数の値を格納するリストを定義します。
R2_list = []
features = list(data_frame.columns)
features.remove("target")
# サンプルサイズ
sample_size = len(data_frame.index)
for number_set in range(k):
# データを学習用とテスト用に分割します。
if number_set < k - 1:
test_data = data_frame[number_set*sample_size//k:(number_set+1)*sample_size//k]
learn_data = pd.concat([data_frame[0:number_set*sample_size//k],data_frame[(number_set+1)*sample_size//k:]])
else:
test_data = data_frame[(k-1)*sample_size//k:]
learn_data = data_frame[:(k-1)*sample_size//k]
# それぞれをラベルと特徴量に分割します
learn_label_data = learn_data["target"]
learn_feature_data = learn_data.loc[:, features]
test_label_data = test_data["target"]
test_feature_data = test_data.loc[:, features]
# SVRのために、それぞれのデータをnumpy.array形式に変換します。
X_test = np.array(test_feature_data)
y_test = np.array(test_label_data)
X_learn = np.array(learn_feature_data)
y_learn = np.array(learn_label_data)
# 回帰分析を行い、テストデータに対するR^2を計算します。
gsvr = grid_search.GridSearchCV(svr, tuned_parameters, cv=5, scoring="mean_squared_error")
gsvr.fit(X_learn, y_learn)
score = gsvr.best_estimator_.score(X_test, y_test)
R2_list.append(score)
# R^2の平均値を返します。
return np.array(R2_list).mean()
if __name__ == "__main__":
from sklearn.datasets import load_boston
from sklearn import svm
import pandas as pd
import random
import numpy as np
# ボストンの家賃のデータを読み込む。
boston = load_boston()
X_data, y_data = boston.data, boston.target
df = pd.DataFrame(X_data, columns=boston["feature_names"])
df['target'] = y_data
count = 0
temp_data = standardize(df)
# 交差検証のためにデータをランダムソートします。
temp_data.reindex(np.random.permutation(temp_data.index)).reset_index(drop=True)
# 各ループにおける特徴量の感度と決定係数を格納するためのdataframeを作ります。
result_data_frame = pd.DataFrame(np.zeros((len(df.columns), len(df.columns))), columns=df.columns)
result_data_frame["決定係数"] = np.zeros(len(df.columns))
# 特徴量を削りきるまで以下のループを実行します。
while(len(temp_data.columns)>1):
# このラウンドにおける残った全特徴量を使用した場合の決定係数です。
result_data_frame.loc[count, "決定係数"] = calculate_R2(temp_data,k=10)
# このラウンドでの特徴量ごとの感度を格納するデータフレームです
temp_features = list(temp_data.columns)
temp_features.remove('target')
temp_result = pd.DataFrame(np.zeros(len(temp_features)),
columns=["abs_Sensitivity"], index=temp_features)
# 各特徴量ごとに以下をループします。
for i, feature in enumerate(temp_data.columns):
if feature == "target":
continue
# 感度分析を行います。
sensitivity = calculate_sensitivity(temp_data, feature)
result_data_frame.loc[count, feature] = sensitivity
temp_result.loc[feature, "abs_Sensitivity"] = abs(sensitivity)
print(feature, sensitivity)
print(count, result_data_frame.loc[count, "決定係数"])
# 感度の絶対値が最小の特徴量をデータから除いたコピーを作ります。
ineffective_feature = temp_result["abs_Sensitivity"].argmin()
print(ineffective_feature)
temp_data = temp_data.drop(ineffective_feature, axis=1)
# データおよび、感度とR^2の推移を返します。
result_data_frame.to_csv("result.csv")
count += 1