はじめに
本記事は、下記のハイパーパラメータチューニングに関する記事の、LightGBMにおける実装例を紹介する記事となります。
※2022/4 early_stoppingの仕様変更について
early_stoppingの指定に関して、以前はfit()メソッドのearly_stopping_round引数で指定する事ができましたが、現在はcallbacks引数にコールバック関数early_stopping()を指定する方法に変わっています。
本記事も新しい仕様に合わせて修正しました。
※2023/6 チューニング手順の改善
本記事に記載されていた手法では以下のような問題が発生していたため、内容を修正いたしました。
-
こちらの記事で述べたように、本記事で紹介していた
callbacks引数にコールバック関数を指定する方法とScikit-learnのcross_val_score()メソッドとを組み合わせると、コールバック関数が初期化されないまま複数の学習が走って正常に処理されないバグが発生します。よってコールバック関数は使用せず、こちらの記事の「第3のearly_stopping指定方法」の方法に則り、LGBMRegressorクラスのコンストラクタにearly_stopping_round引数を渡す方法に変更しました。 -
early_stopping用のデータ(eval_set)に全データをしていたため、リークが発生していました。よってリークを防ぐため、以下の図のようにearly_stopping用のデータを別途分割するように修正しました(より発展的なデータ分割法はこちらも参照ください)
特に2の変更によりearly_stoppingによる学習の打ち切りが早くなった(以前の方法ではeval_setに学習データが含まれていたため、学習継続によるeval_setに対する性能向上が過学習気味となるまで進み、時間が掛かっていた)ため、どの手法でもチューニングの所要時間が50秒オーダー → 5秒オーダーまで1桁も短くなりました(過学習も防げて一石二鳥だと思います)
LightGBMとパラメータチューニング
LightGBMは分類や回帰に用いられる機械学習アルゴリズムで、その性能の高さや使い勝手の良さ(特徴量重要度などが出せる)から、特に回帰においてはXGBoostと並ぶメジャーなアルゴリズムです。
XGBoostと比較したとき、LightGBMは動作が軽量で大規模データの学習に強いと言われています。
一方でLightGBMは多くのハイパーパラメータを持つため、その性能を十分に発揮するためにはパラメータチューニングが重要となります。
チューニング対象のパラメータ
LightGBMの主なパラメータは、こちらの記事で分かりやすく解説されています。
全てのパラメータは、こちらの公式ドキュメントで解説されています
LightGBMは他の回帰アルゴリズム(例:ラッソ回帰(1種類)、SVR(3種類))と比べてパラメータの数が多く、また使用するAPI(Scikit-learn API or Training API)によってパラメータの数が変わるなど、複雑なパラメータ構成を持っています。
そのため、全てのパラメータをチューニング対象とすると制御が難しく、一部の重要なパラメータのみを選んでチューニング対象とすることが一般的です。
本記事で使用するパラメータ
本記事では、Optuna公式サンプルコードのチューニング対象パラメータを使用します。
またチューニングに先立ち、学習に使用するAPIおよびboosterのタイプ(boosting type)を選択する必要があります。今回は
| 選択内容 | 選択する方式 | 選択理由 |
|---|---|---|
| API | Scikit-Learn API | Scikit-Learnの各種チューニング用メソッドを利用するため |
| boosting type | gbdt | 最もよく使われる方式(他方式との差はこちら参照) |
を採用します。
この際、Scikit-learn APIとTraining APIで一部パラメータの名称が異なるのでご注意ください
今回使用するパラメータ一覧と、対応する名称を下記します
| Scikit-Learn APIでの名称 |
Training APIでの 名称 |
型 (スケール) | 範囲 | デフォルト値 | 内容 |
|---|---|---|---|---|---|
| reg_alpha | lambda_l1 | float (log) | 0-∞ | 0 | L1正則化項の係数(小さいほど過学習寄り) |
| reg_lambda | lambda_l2 | float (log) | 0-∞ | 0 | L2正則化項の係数(小さいほど過学習寄り) |
| num_leaves | num_leaves | int (linear) | 2-131072 | 31 | 1本の木の最大葉枚数(大きいほど過学習寄り) |
| colsample _bytree | feature_fraction | float (linear) | 0-1 | 1.0 | 各決定木においてランダムに抽出される列の割合(大きいほど過学習寄り) |
| subsample | bagging_fraction | float (linear) | 0-1 | 1.0 | 各決定木においてランダムに抽出される標本の割合(大きいほど過学習寄り) |
| subsample_freq | bagging_freq | int (linear) | 0-∞ | 0 | ここで指定したイテレーション毎にバギング実施(大きいほど過学習寄りだが、0のときバギング非実施となるので注意) |
| min_child_samples | min_data_in_leaf | int (linear) | 0-∞ | 20 | 1枚の葉に含まれる最小データ数(小さいほど過学習寄り) |
実装
下図のフロー(こちらの記事と同じ)に基づき、LightGBM回帰におけるチューニングを実装します
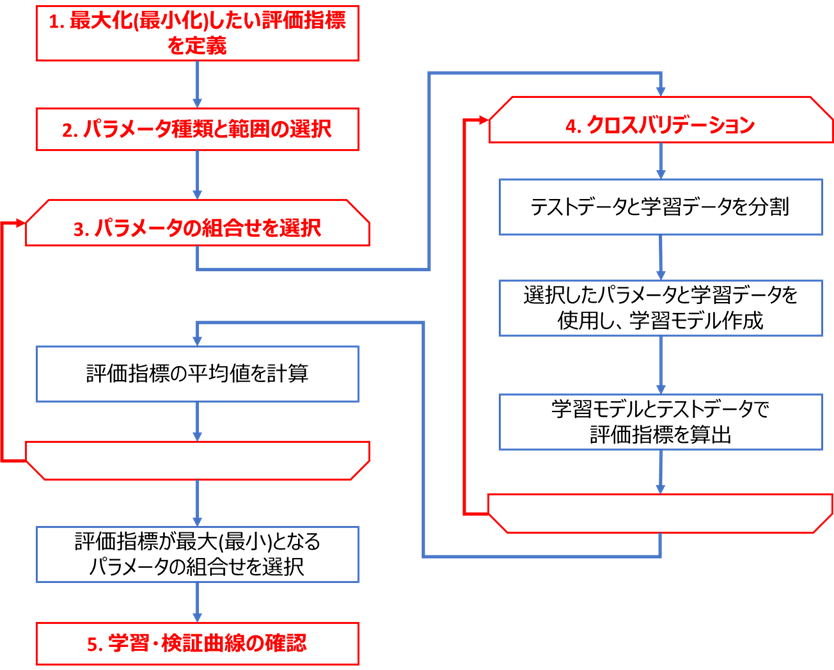
コードはこちらのGitHub(lgbm_tuning_tutorials.py)にもアップロードしております。
また、希望があればLightGBM分類の記事も作成しますので、コメント欄に記載いただければと思います。
実装に必要な環境整備
ライブラリ
チューニングの実装に必要なライブラリ等をインストールします。
私の環境では、以下のライブラリを使用しています
・Python本体 (動作確認時は3.9.5を使用)
・Matplotlibで表示可能な環境 (Jupyter等)
・下記ライブラリ (参考として動作確認時のライブラリバージョンも記載)
lightgbm (3.2.1)
scikit-learn (0.24.2)
bayesian-optimization (1.2.0)
optuna (2.7.0)
numpy (1.20.3)
pandas (1.2.4)
seaborn (0.11.0)
matplotlib (3.4.2)
・こちらの回帰可視化ライブラリ(チューニング前後のモデル可視化にのみ使用するので、なくともチューニング自体はできます)
使用するサンプルデータ
こちらの記事の、大阪都構想選挙データを使用します
ハードウェア
チューニング速度はCPU等の性能に大きく依存します
参考までに本記事で使用したPC(Lenovoのモバイル)のスペックを下記します
| デバイス | スペック |
|---|---|
| CPU | Intel Core i5-8250U@1.6GHz |
| メモリ | 8GB(4+4) DDR4 2400MHz SODIMM |
| ストレージ | SSD PCIe M.2 |
| OS | Windows 10 Pro 64bit |
コードの実行にはVSCodeのJupyter拡張を使用しております。
CPUやメモリの使用状況にもチューニングは左右されますが、余計なプロセスを終了してからチューニングを開始することで、繰り返してもほぼ同じ所要時間となり、再現性のとれる結果となりました。
実際の実装例
前述のフローに基づき実装を進めていきます
データの読込
こちらのデータセットをCSVからPandasのDataFrame(Jupyterでの表示用)およびNumpyのndarray(LightGBMモデルへの読込用)に読み込みます
import pandas as pd
import time
df_osaka = pd.read_csv(f'./sample_data/osaka_metropolis_english.csv')
OBJECTIVE_VARIALBLE = 'approval_rate' # 目的変数
USE_EXPLANATORY = ['2_between_30to60', '3_male_ratio', '5_household_member', 'latitude'] # 説明変数
y = df_osaka[OBJECTIVE_VARIALBLE].values # 目的変数をndarray化
X = df_osaka[USE_EXPLANATORY].values # 説明変数をndarray化
# データを表示
df_osaka[USE_EXPLANATORY + [OBJECTIVE_VARIALBLE]]
2_between_30to60 3_male_ratio 5_household_member latitude approval_rate
0 0.499141 0.485807 1.83 42.325 0.562728
1 0.425080 0.481006 2.10 42.078 0.526104
2 0.467986 0.473394 2.06 41.535 0.536686
3 0.411267 0.473798 2.20 40.197 0.496048
4 0.390663 0.473722 2.16 43.273 0.471734
5 0.419868 0.474112 2.25 42.190 0.504592
6 0.422815 0.475847 2.52 42.257 0.511019
7 0.342897 0.577474 1.75 38.090 0.492851
8 0.506583 0.468446 1.65 40.870 0.509798
9 0.496780 0.467432 1.96 40.575 0.538094
10 0.374845 0.486567 2.34 39.018 0.465384
11 0.462086 0.505250 1.61 39.560 0.516693
12 0.383394 0.478802 2.36 36.575 0.486810
13 0.392461 0.465524 2.15 36.222 0.450049
14 0.390136 0.471774 2.38 37.270 0.456477
15 0.450164 0.464464 2.06 39.467 0.478386
16 0.368153 0.480087 2.27 39.218 0.480658
17 0.409648 0.460738 2.22 38.316 0.450814
18 0.386937 0.469701 2.23 37.322 0.473037
19 0.402482 0.488469 2.29 40.980 0.468385
20 0.400149 0.486460 2.18 39.835 0.429843
21 0.406196 0.490601 2.35 42.683 0.473805
22 0.433488 0.496974 1.97 43.260 0.550678
23 0.409827 0.491403 1.99 44.470 0.502997
クロスバリデーション用データとearly_stopping用のデータを分割
クロスバリデーション時のテストデータや学習データにearly_stoppingの評価用データが混入する事(データリーク)を防ぎ、過学習を抑止するため、下図のようにクロスバリデーション用データとearly_stopping用のデータを分割します。
以下のX_cvおよびy_cvがクロスバリデーション用データ、X_evalおよびy_evalがearly_stopping用のデータとなります。
from sklearn.model_selection import train_test_split
seed = 42 # 乱数シード
X_cv, X_eval, y_cv, y_eval = train_test_split(X, y, test_size=0.25, random_state=42)
チューニング前のモデルの確認
こちらのライブラリで、チューニング前モデルの特徴量と目的変数の関係を可視化します
from seaborn_analyzer import regplot
from lightgbm import LGBMRegressor
from sklearn.model_selection import KFold
# 使用するチューニング対象外のパラメータ
params = {
'objective': 'regression', # 最小化させるべき損失関数
'metric': 'rmse', # 学習時に使用する評価指標(early_stoppingの評価指標にも同じ値が使用される)
'random_state': seed, # 乱数シード
'boosting_type': 'gbdt', # boosting_type
'n_estimators': 10000, # 最大学習サイクル数。early_stopping使用時は大きな値を入力
'verbose': -1, # これを指定しないと`No further splits with positive gain, best gain: -inf`というWarningが表示される
'early_stopping_round': 10 # ここでearly_stoppingを指定
}
# モデル作成
model = LGBMRegressor(**params)
# 学習時fitパラメータ指定 (early_stopping用のデータeval_setを渡す)
fit_params = {
'eval_set': [(X_eval, y_eval)]
}
# クロスバリデーションして予測値ヒートマップを可視化
cv = KFold(n_splits=3, shuffle=True, random_state=seed) # KFoldでクロスバリデーション分割指定
regplot.regression_heat_plot(model, x=X_cv, y=y_cv, x_colnames=USE_EXPLANATORY,
pair_sigmarange = 0.5, rounddigit_x1=3, rounddigit_x2=3,
cv=cv, display_cv_indices=0,
fit_params=fit_params, validation_fraction=None)
全ての条件で同じ予測値(色の濃さ)となっており、うまく回帰できていないことが分かります。
チューニングでの改善が必要だと一目で分かります。
ちなみに、LGBMRegressorはScikit-Learn APIにおけるLightGBM回帰を実行するクラスで、objectiveが学習時に使用する評価指標、random_stateが使用する乱数シードです。
・early_stopping_roundsについて
LightGBMにはearly_stopping_roundsという便利な機能があります。
XGBoostやLightGBMは学習を繰り返すことで性能を上げていくアルゴリズムですが、学習回数を増やしすぎると性能向上が止まって横ばいとなり、無意味な学習を繰り返して学習時間増加の原因となってしまいます(参考)
early_stopping_roundsは、この学習回数を適切なタイミングで打ち止めるための仕組みで、「○回連続で評価指標が向上しなくなったら、学習を打ち止める」というアルゴリズムとなっています。
後述のように、early_stoppingなしで学習を進めると学習が進みすぎたり(過学習)、逆に収束していないのに学習を打ち切る(未学習)事もあるので、基本的にはearly_stopping_roundsを指定した方が良いといえるでしょう
Scikit-Learn APIのLightGBMでearly_stopping_roundsを利用する場合、
fit_params引数にdict形式でcallback、eval_metricおよびeval_setを指定します。
→前述のように、コールバック関数を使用するとLGBMRegressorクラスのコンストラクタにearly_stopping_round引数を渡す方法(こちらの記事の「第3のearly_stopping指定方法」)でearly_stoppingを指定します。
また、early_stoppingの指定に伴い、以下の操作が必要となります。
-
early_stopping条件を満たす前に学習が打ち切られないよう、
n_estimatorsに大きな値(例:10000)を指定する必要があります。 -
学習用パラメータ
fit_paramsのeval_setにearly_stoppingの評価用データを渡します。eval_setは本来であれば検証用データを入れる事が望ましいですが、cross_val_scoreメソッドの外側で検証用データを分けることができないので、本記事ではCV分割前のデータをそのまま入力します。
→前述のようにこの方法ではクロスバリデーション用データと混在してデータリークが発生する(クロスバリデーションの学習データで性能が上がらなくなるまで学習が進んで過学習気味となったり、評価データに過適合してしまったりする)ため、下図のように先ほど分けたearly_stopping用評価データを渡します
- パラメータとして指定するmetricおよびobjectiveは、後述の「手順1」で指定する評価指標に合わせることが望ましいです。
| 評価指標の名称 | 手順1の評価指標 | objective | metric |
|---|---|---|---|
| RMSE | 'neg_root_mean_squared_error'または'neg_mean_squared_error' | 'regression' | 'rmse' |
| MAE | 'neg_mean_absolute_error' | 'regression_l1' | 'mae' |
※ざっと見た限りでは、RMSLEに相当するobjectiveやeval_metricは存在しなさそうです
参考までに、分類での評価指標も列記します
(APIドキュメントを見る限りobjectiveはLogLossしか存在しないので、全ての指標を揃えようとすると実質LogLoss一択となりそうです。手順1の評価指標とeval_metricはAUCなども選択できます。詳しくはリンクを参照ください)
| 評価指標の名称 | 手順1の評価指標 | objective | eval_metric |
|---|---|---|---|
| LogLoss (2値分類) | 'neg_log_loss' | 'binary' | 'binary_logloss' |
| LogLoss (多クラス分類) | 'neg_log_loss' | 'multiclass' | 'multi_logloss' |
以上まとめると、前述の「チューニング前のモデルの確認」のサンプルコードのうち、以下でコメントしている部分がearly_stoppingに関連するパラメータ指定となります。
# 使用するチューニング対象外のパラメータ
params = {
'objective': 'regression', # 最小化させるべき損失関数
'metric': 'rmse', # 学習時に使用する評価指標(early_stoppingの評価指標にも同じ値が使用される)
'random_state': seed, # 乱数シード
'boosting_type': 'gbdt',
'n_estimators': 10000, # 最大学習サイクル数。early_stopping使用時は大きな値を入力
'verbose': -1, # これを指定しないと`No further splits with positive gain, best gain: -inf`というWarningが表示される
'early_stopping_round': 10 # ここでearly_stoppingを指定
}
# モデル作成
model = LGBMRegressor(**params)
# 学習時fitパラメータ指定
fit_params = {
'eval_set': [(X_eval, y_eval)] # early_stopping用のデータeval_setを渡す
}
手順1 最大化したい評価指標の定義
今回は
・回帰
・外れ値が多いデータではない
ので、こちらのフローに基づきRMSE(Scikit-Learnでは'neg_root_mean_squared_error')を採用します。
チューニング前の評価指標をクロスバリデーションで算出します。
from sklearn.model_selection import cross_val_score
import numpy as np
scoring = 'neg_root_mean_squared_error' # 評価指標をRMSEに指定
# クロスバリデーションで評価指標算出
scores = cross_val_score(model, X_cv, y_cv, cv=cv,
scoring=scoring, n_jobs=-1, fit_params=fit_params)
print(f'scores={scores}')
print(f'average_score={np.mean(scores)}')
scores=[-0.02426901 -0.03971342 -0.0280086 ]
average_score=-0.030663676536520218
チューニング前のスコア(neg_mean_squared_error = -MSE)は-0.03066であることが分かりました。
前述の可視化の時点で予見はできましたが、XGBoostのときと比べるとかなり悪い値となっています。
チューニングでこの値を改善していきます
手順2 パラメータ種類と範囲の選択
・種類
Optunaサンプルコードに基づき、前述の7パラメータを使用します
・範囲
適当な初期範囲を定めて検証曲線をプロットし、その結果に基づいて範囲を調整していきます。
from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
cv_params = {'reg_alpha': [0, 0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10],
'reg_lambda': [0, 0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10],
'num_leaves': [2, 4, 8, 16, 32, 64, 96, 128, 160, 192, 224, 256],
'colsample_bytree': [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample': [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample_freq': [0, 1, 2, 3, 4, 5, 6, 7],
'min_child_samples': [0, 2, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
}
param_scales = {'reg_alpha': 'log',
'reg_lambda': 'log',
'num_leaves': 'linear',
'colsample_bytree': 'linear',
'subsample': 'linear',
'subsample_freq': 'linear',
'min_child_samples': 'linear'
}
# 検証曲線のプロット(パラメータ毎にプロット)
for i, (k, v) in enumerate(cv_params.items()):
train_scores, valid_scores = validation_curve(estimator=model,
X=X_cv, y=y_cv,
param_name=k,
param_range=v,
fit_params=fit_params,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# スケールをparam_scalesに合わせて変更
plt.xscale(param_scales[k])
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()

ほとんどのパラメータで変化が見られませんが、min_child_samplesのみ変化が見られます。
これはサンプル数23に対し、min_child_samplesのデフォルト値20が大きすぎることが原因です。
同様にnum_leavesのデフォルト値31も大きすぎるので、
min_child_samples=5
num_leaves=2
に変更し、再度検証曲線をプロットします。
from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
model.set_params(min_child_samples=5, num_leaves=2)
# 検証曲線のプロット(パラメータ毎にプロット)
for i, (k, v) in enumerate(cv_params.items()):
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
fit_params=fit_params,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# スケールを'log'に(線形なパラメータは'linear'にするので注意)
plt.xscale(param_scales[k])
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()
SVMのときほど顕著な傾向は出ていませんが、過学習または未学習になり過ぎない範囲を基準に、以下のようにチューニング範囲を定めます

手順3&4 パラメータ選択&クロスバリデーション
SVMのときと同様に、下記A、B、C (BayesianOptimization)、C (Optuna)の4種類の実装法をそれぞれ解説します。
| 名称 | 概要 | メリット | デメリット | ライブラリ | |
|---|---|---|---|---|---|
| A | グリッドサーチ | パラメータを格子状に総当たり | シンプルで結果解釈性が高い | 計算時間がかかる | Scikit-Learn |
| B | ランダムサーチ | パラメータをランダムに決定 | 平均的にはグリッドサーチより速い | 運任せの要素あり | Scikit-Learn |
| C | ベイズ最適化 | 前回結果に基づきパラメータ決定 | ランダムサーチより速い | ライブラリ操作がやや難 | BayesianOptimization, Optuna |
また、SVMと比べLightGBMは処理が重い(XGBoostほどではありませんが)ため、チューニング時間が課題となります。
スコアと共にチューニングにかかった時間も測定し、各アルゴリズムで比較してみます。
処理時間は試行数にも依存するため、後述のearly_stopping_roundなしのとき(=パラメータによる学習の収束速度に左右されない)のチューニング時間が等しくなる、という基準で、各アルゴリズムの試行数を定めました
| 名称 | 試行数 | early_stopping_roundなし時のチューニング所要時間 |
|---|---|---|
| グリッドサーチ | 1152 |
48秒 |
| ランダムサーチ | 1120 | 43秒 |
| ベイズ最適化 (Bayesian Optimization) |
100 (初期20+ベイズ80) |
50秒 |
| ベイズ最適化 (Optuna) |
400 | 49秒 |
グリッドサーチの場合
GridSearchCVクラスで、グリッドサーチによる最適化を実行します。
下記のようにパラメータの組合せ(3x2x4x3x2x2x4=1152通り)を設定し、グリッドサーチを実行します
from sklearn.model_selection import GridSearchCV
start = time.time()
# 最終的なパラメータ範囲(1152通り)
cv_params = {'reg_alpha': [0.0001, 0.003, 0.1],
'reg_lambda': [0.0001, 0.1],
'num_leaves': [2, 3, 4, 6],
'colsample_bytree': [0.4, 0.7, 1.0],
'subsample': [0.4, 1.0],
'subsample_freq': [0, 7],
'min_child_samples': [0, 2, 5, 10]
}
# グリッドサーチのインスタンス作成
gridcv = GridSearchCV(model, cv_params, cv=cv,
scoring=scoring, n_jobs=-1)
# グリッドサーチ実行(学習実行)
gridcv.fit(X, y, **fit_params)
# 最適パラメータの表示と保持
best_params = gridcv.best_params_
best_score = gridcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
最適パラメータ {'colsample_bytree': 0.4, 'min_child_samples': 0, 'num_leaves': 3, 'reg_alpha': 0.0001, 'reg_lambda': 0.1, 'subsample': 0.4, 'subsample_freq': 7}
スコア -0.020678449955621545
所要時間5.106598138809204秒
reg_alpha=0.0001
reg_lambda=0.1
num_leaves=3
colsample_bytree=0.4
subsample=0.4
subsample_freq=7
min_child_samples=0
のときに評価指標neg_root_mean_squared_errorが最大となり、その時の評価指標は-0.02067‥であることが分かります。
パラメータの値と学習速度について
XGBoostのときほどではありませんが、後述のearly_stopping_roundを設定しないときと比べてやや所要時間が増えています。自作ライブラリ(後日公開&記事化します)でパラメータと所要時間の関係を測定したところ、下図のように一部のパラメータの値に応じて学習時間が増える(収束速度が遅くなる)ことが分かりました。
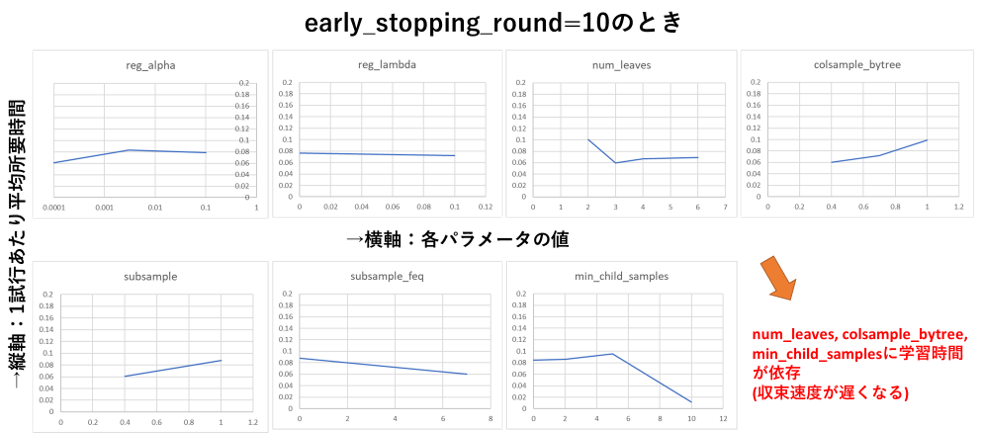

early_stopping_roundを指定しなければこの速度低下が防げるように見えますが、この場合は収束していないのに学習を打ち切っているため、学習性能ををフルに発揮できていないという意味で、やはり避けるべき状況です。
とはいえXGBoostのときと比べるとパラメータの値による学習時間の変化は小さいので、LightGBMに関してはパラメータの値による速度低下にはそれほど神経質にならなくともよいかと思います。
ランダムサーチの場合
RondomizedSearchCVクラスで、ランダムサーチによる最適化を実行します
from sklearn.model_selection import RandomizedSearchCV
start = time.time()
# パラメータの種類と密度をグリッドサーチのときより増やす
cv_params = {'reg_alpha': [0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1],
'reg_lambda': [0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1],
'num_leaves': [2, 3, 4, 5, 6],
'colsample_bytree': [0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample': [0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample_freq': [0, 1, 2, 3, 4, 5, 6, 7],
'min_child_samples': [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
}
# ランダムサーチのインスタンス作成
randcv = RandomizedSearchCV(model, cv_params, cv=cv,
scoring=scoring, random_state=seed,
n_iter=1120, n_jobs=-1)
# ランダムサーチ実行(学習実行)
randcv.fit(X, y, **fit_params)
# 最適パラメータの表示と保持
best_params = randcv.best_params_
best_score = randcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
最適パラメータ {'subsample_freq': 5, 'subsample': 0.5, 'reg_lambda': 0.0001, 'reg_alpha': 0.01, 'num_leaves': 6, 'min_child_samples': 0, 'colsample_bytree': 0.7}
スコア -0.019266490467137198
所要時間5.083421230316162秒
reg_alpha=0.01
reg_lambda=0.0001
num_leaves=6
colsample_bytree=0.7
subsample=0.5
subsample_freq=5
min_child_samples=0
のときに評価指標neg_root_mean_squared_errorが最大となり、その時の評価指標は-0.01926‥であることが分かります。
ベイズ最適化(BayesianOptimization)の場合
BayesianOptimizationによるベイズ最適化の実装法を解説します。
3.1の教訓に基づき、今回は最初から対数スケールに対応した実装法を採用します
from bayes_opt import BayesianOptimization
from bayes_opt.util import UtilityFunction
start = time.time()
# パラメータ範囲(Tupleで範囲選択)
bayes_params = {'reg_alpha': (0.0001, 0.1),
'reg_lambda': (0.0001, 0.1),
'num_leaves': (2, 6),
'colsample_bytree': (0.4, 1.0),
'subsample': (0.4, 1.0),
'subsample_freq': (0, 7),
'min_child_samples': (0, 10)
}
# 対数スケールパラメータを対数化
param_scales = {'reg_alpha': 'log',
'reg_lambda': 'log',
'num_leaves': 'linear',
'colsample_bytree': 'linear',
'subsample': 'linear',
'subsample_freq': 'linear',
'min_child_samples': 'linear'
}
bayes_params_log = {k: (np.log10(v[0]), np.log10(v[1])) if param_scales[k] == 'log' else v for k, v in bayes_params.items()}
# 整数型パラメータを指定
int_params = ['num_leaves', 'subsample_freq', 'min_child_samples']
# ベイズ最適化時の評価指標算出メソッド(引数が多いので**kwargsで一括読込)
def bayes_evaluate(**kwargs):
params = kwargs
# 対数スケールパラメータは10のべき乗をとる
params = {k: np.power(10, v) if param_scales[k] == 'log' else v for k, v in params.items()}
# 整数型パラメータを整数化
params = {k: round(v) if k in int_params else v for k, v in params.items()}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X_cv, y_cv, cv=cv,
scoring=scoring, fit_params=fit_params, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
bo = BayesianOptimization(bayes_evaluate, bayes_params_log, random_state=seed)
bo.maximize(init_points=10, n_iter=80, acquisition_function=UtilityFunction(kind='ei'))
# 最適パラメータとスコアを取得
best_params = bo.max['params']
best_score = bo.max['target']
# 対数スケールパラメータは10のべき乗をとる
best_params = {k: np.power(10, v) if param_scales[k] == 'log' else v for k, v in best_params.items()}
# 整数型パラメータを整数化
best_params = {k: round(v) if k in int_params else v for k, v in best_params.items()}
# 最適パラメータを表示
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
※bo.maximizeの引数init_points, n_iter, acqは、こちらを参考に適宜変更してください
※2023/6 引数acqは廃止となり、代わりにbayes_opt.util.UtilityFunctionクラスのインスタンスにkindという引数を渡すように変わりました
最適パラメータ {'colsample_bytree': 0.49472366423832387, 'min_child_samples': 2, 'num_leaves': 2, 'reg_alpha': 0.00022419339244248538, 'reg_lambda': 0.014662179397607401, 'subsample': 0.5339011849231865, 'subsample_freq': 3}
スコア -0.02038260702894278
所要時間12.983080863952637秒
reg_alpha=0.000224
reg_lambda=0.0146
num_leaves=2
colsample_bytree=0.494
subsample=0.533
subsample_freq=3
min_child_samples=2
のときに評価指標neg_root_mean_squared_errorが最大となり、その時の評価指標は-0.02038‥であることが分かります。
ベイズ最適化(Optuna)の場合
Optunaによるベイズ最適化の実装法を解説します。
import optuna
start = time.time()
# ベイズ最適化時の評価指標算出メソッド
def bayes_objective(trial):
params = {
'reg_alpha': trial.suggest_float('reg_alpha', 0.0001, 0.1, log=True),
'reg_lambda': trial.suggest_float('reg_lambda', 0.0001, 0.1, log=True),
'num_leaves': trial.suggest_int('num_leaves', 2, 6),
'colsample_bytree': trial.suggest_float('colsample_bytree', 0.4, 1.0),
'subsample': trial.suggest_float('subsample', 0.4, 1.0),
'subsample_freq': trial.suggest_int('subsample_freq', 0, 7),
'min_child_samples': trial.suggest_int('min_child_samples', 0, 10)
}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, fit_params=fit_params, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
study = optuna.create_study(direction='maximize',
sampler=optuna.samplers.TPESampler(seed=seed))
study.optimize(bayes_objective, n_trials=400)
# 最適パラメータの表示と保持
best_params = study.best_trial.params
best_score = study.best_trial.value
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
最適パラメータ {'reg_alpha': 0.018620206062640105, 'reg_lambda': 0.0002338703193119407, 'num_leaves': 4, 'colsample_bytree': 0.8187799960140917, 'subsample': 0.46815071845841244, 'subsample_freq': 3, 'min_child_samples': 0}
スコア -0.01968648683818964
所要時間7.056947946548462秒
reg_alpha=0.0186
reg_lambda=0.000233
num_leaves=4
colsample_bytree=0.818
subsample=0.468
subsample_freq=3
min_child_samples=0
のときに評価指標neg_root_mean_squared_errorが最大となり、その時の評価指標は-0.01968‥であることが分かります。
以上、4種類のアルゴリズムでのチューニング結果をまとめると、下の表のようになります。
| 名称 | 試行数 | スコア(大きいほどGood) | 所要時間 |
|---|---|---|---|
| グリッドサーチ | 1124 | -0.02067 | 5.1秒 |
| ランダムサーチ | 1120 | -0.01926 | 5.1秒 |
| ベイズ最適化 (Bayesian Optimization) |
100 | -0.02038 | 13.0秒 |
| ベイズ最適化 (Optuna) |
400 | -0.01968 | 7.1秒 |
スコアに関しては、ランダムサーチとOptunaによるベイズ最適化がよさそうです。
所要時間に関してはBayesian OptimizationやOptunaが長めとなっていますが、これらのパッケージは単純なグリッドサーチやランダムサーチと比べてオーバーヘッドが大きいため、今回のようにデータ数が少なく学習速度が速いケースでは、オーバーヘッドの割合が多くなって計算が遅くなることが原因だと考えています。私の経験上では、ある程度のデータ数があれば基本的にはOptunaが最も早く良いスコアに収束します。
※参考:early_stopping_round不使用時のチューニング結果
上記のパターンではグリッドサーチが多くの時間が掛かっていますが、early_stopping_roundを指定しない場合(常にデフォルトの学習回数100回を使用)では、他のアルゴリズムとほぼ同時間で処理が完了できます(前述の収束前に学習が終了する問題はありますが‥)
参考までに、early_stopping_roundを指定しない場合のスコアと所要時間を下記します
最適パラメータ {'colsample_bytree': 0.4, 'min_child_samples': 0, 'num_leaves': 4, 'reg_alpha': 0.0001, 'reg_lambda': 0.0001, 'subsample': 0.4, 'subsample_freq': 0}
スコア -0.020057553
所要時間48.24397921562195秒
最適パラメータ {'subsample_freq': 3, 'subsample': 0.5, 'reg_lambda': 0.001, 'reg_alpha': 0.001, 'num_leaves': 4, 'min_child_samples': 3, 'colsample_bytree': 0.7}
スコア -0.019135444
所要時間43.027225971221924秒
最適パラメータ {'colsample_bytree': 0.9430083037075744, 'min_child_samples': 3, 'num_leaves': 2, 'reg_alpha': 0.0020869096632570856, 'reg_lambda': 0.0020382643364640087, 'subsample': 0.5853280069552931, 'subsample_freq': 2}
スコア -0.019237461
所要時間50.49155378341675秒
最適パラメータ {'reg_alpha': 0.0023317132133850566, 'reg_lambda': 0.0006717623390065321, 'num_leaves': 5, 'colsample_bytree': 0.926079384200066, 'subsample': 0.4948413802207167, 'subsample_freq': 4, 'min_child_samples': 0}
スコア -0.01541169
所要時間48.97835183143616秒
いずれにせよ、Optunaが最も効率よくチューニングできていることが分かります。Optunaの性能恐るべしですね!
(なお、今回のケースではearly_stopping用のデータを確保する必要がないため、全てのデータをクロスバリデーションに使用しています)
手順5 学習・検証曲線の確認
学習、検証曲線で過学習の有無を確認します。
今回はOptunaで調整したパラメータ(reg_alpha=0.0186‥, reg_lambda=0.000233‥)を例に描画してみます。
学習曲線
学習曲線をプロットし、
・目標性能を達成しているか
・過学習していないか
を確認します
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
# 最適パラメータを学習器にセット
model.set_params(**best_params)
# 学習曲線の取得
train_sizes, train_scores, valid_scores = learning_curve(estimator=model,
X=X_cv, y=y_cv,
train_sizes=np.linspace(0.1, 1.0, 10),
fit_params=fit_params,
cv=cv, scoring=scoring, n_jobs=-1)
# 学習データ指標の平均±標準偏差を計算
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# 検証データ指標の平均±標準偏差を計算
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(train_sizes, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(train_sizes, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(train_sizes, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(train_sizes, valid_high, valid_low, alpha=0.15, color='green')
# 最高スコアの表示
best_score = valid_center[len(valid_center) - 1]
plt.text(np.amax(train_sizes), valid_low[len(valid_low) - 1], f'best_score={best_score}',
color='black', verticalalignment='top', horizontalalignment='right')
# 軸ラベルおよび凡例の指定
plt.xlabel('training examples') # 学習サンプル数を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例

こちらのの確認方法に基づいて確認すると、下記のようにOKと判断できます
・目的の性能を達成しているか → 目標性能は定めていないが、チューニング前より大幅向上(-0.03066 → -0.01968)したのでOKとする
・過学習していないか → データ数が少ないので断定はできないが、ある程度検証データ指標と学習データ指標が収束しているのでOKとする
検証曲線
検証曲線をプロットし、
・性能の最大値を捉えられているか
・過学習していないか
を確認します
from sklearn.model_selection import validation_curve
# 検証曲線描画対象パラメータ
valid_curve_params = {'reg_alpha': [0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1],
'reg_lambda': [0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1],
'num_leaves': [2, 3, 4, 5, 6],
'colsample_bytree': [0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample': [0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample_freq': [0, 1, 2, 3, 4, 5, 6, 7],
'min_child_samples': [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
}
param_scales = {'reg_alpha': 'log',
'reg_lambda': 'log',
'num_leaves': 'linear',
'colsample_bytree': 'linear',
'subsample': 'linear',
'subsample_freq': 'linear',
'min_child_samples': 'linear'
}
# 最適パラメータを上記描画対象に追加
for k, v in valid_curve_params.items():
if best_params[k] not in v:
v.append(best_params[k])
v.sort()
for i, (k, v) in enumerate(valid_curve_params.items()):
# モデルに最適パラメータを適用
model.set_params(**best_params)
# 検証曲線を描画
train_scores, valid_scores = validation_curve(estimator=model,
X=X_cv, y=y_cv,
param_name=k,
param_range=v,
fit_params=fit_params,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# 最適パラメータを縦線表示
plt.axvline(x=best_params[k], color='gray')
# スケールをparam_scalesに合わせて変更
plt.xscale(param_scales[k])
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()

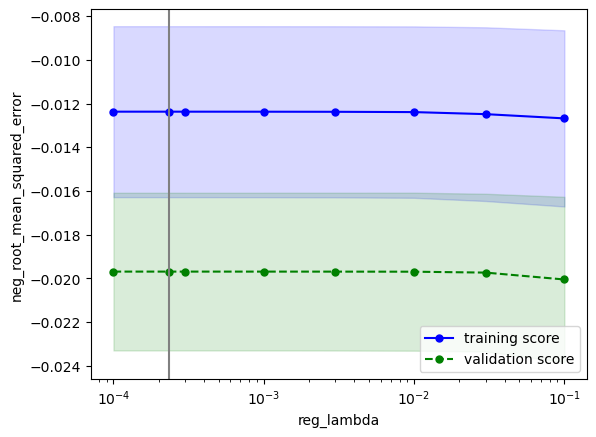




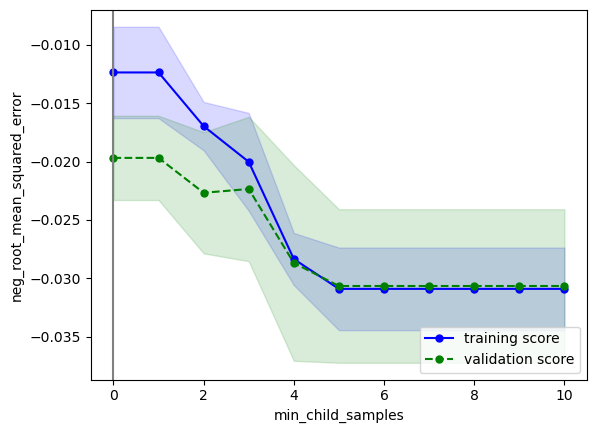
こちらの確認方法に基づいて確認すると、下記のようにOKと判断できます
・性能の最大値を捉えられているか → どのパラメータもだいたい捉えられていそうなのでOKとする
・過学習していないか → データ数が少ないために多少の乖離はあるが、最適パラメータにおいて学習データ指標と検証データ指標が近づいているのでOK
※パラメータreg_lambdaに関してはチューニング後のパラメータ値よりも性能が高くなる部分がありますが、これはチューニング時のパラメータの組合せとは無関係に、検証曲線のパラメータの組合せを選んでいることに起因します。
ベイズ最適化においてはこのような事は往々に起こりますが、まだ改善の余地があると言えるので、気になる方はn_trialsを増やして再実行するのが良いかと思います
チューニング後のモデルを可視化
最後に、チューニング後のモデルを可視化します(チューニング前と比較)
regplot.regression_heat_plot(model, x=X_cv, y=y_cv, x_colnames=USE_EXPLANATORY,
pair_sigmarange = 0.5, rounddigit_x1=3, rounddigit_x2=3,
cv=cv, display_cv_indices=0,
fit_params=fit_params, estimator_params=best_params)
チューニング前は予測値が一定でうまく回帰できていませんでしたが、
チューニング後は男性比率(3_male_ratio)が高いほど、30-60代(2_between_30to60)が多いほど、北に(latitude)行くほど賛成率(approval_rate)が高い=色が濃いことが分かり、傾向が捉えられていることが分かります。
チューニング成功と言って良いのではないかと思います。
まとめ
・LightGBMのパラメータチューニングを、7パラメータを選択して実施
・4種類のアルゴリズムのうち、Optunaが速度、評価指標両方で最も優れていた
・一部のパラメータは学習時間に影響を与えるため、範囲を広くとるとグリッドサーチの速度低下に繋がる
おまけ:OptunaのLightGBM専用チューニング
Optuna1.5.0より、LightGBMをクロスバリデーションでチューニングするLightGBMTunerCVというクラスが追加されたようです。
パラメータを細かく指定する必要がないので簡単にチューニングでき、かつ「重要なハイパーパラメータから順に最適なハイパーパラメータをチューニングする」ことで、効率的にチューニングができるそうです。
詳しくは公式APIリファレンスや公式の紹介記事を参照ください
使用法は以下の記事が分かりやすいです
公式のサンプルコードも使用法の参考になるかと思います




