はじめに
売り上げなどの数量(連続値をとる目的変数)を予測するのに役立つのが回帰です。この記事では、特に目的変数と説明変数の関係をモデル化する一つの方法である線形回帰をScikit-learnライブラリを使って行う方法について、備忘録として書いておきます。
Scikit-learn について
Scikit-learnは、Pythonの機械学習ライブラリの一つです。
線形回帰について
線形回帰は、連続値をとる目的変数 $y$ と説明変数 $x$(特徴量)の線形関係をモデル化します。線形関係とは、平たく言うと、説明変数が増加(減少)するのに応じて、目的変数も単調に増加(減少)する関係です。説明変数が一つの場合(単回帰と呼ぶ)、目的変数と説明変数の関係をモデル化する線形モデルは以下の式で定義されます。
y = w_0 + w_1x
ここで、重み $w_0$ は切片、重み $w_1$ は説明変数の係数を表します。線形回帰の目的は、説明変数と目的変数の関係を表現する線形モデルの重みを学習することです。上の式のように、目的変数が説明変数の一次式で表現されるとき、線形回帰は「説明変数と目的変数の散布図において、データの分布を最もよく特徴づける直線を探し出すこと」といえます。
説明変数が複数の場合(重回帰と呼ぶ)、目的変数を説明変数の線形和で表現する線形モデルは以下の式で定義されます。
y = w_0x_0 + w_1x_1 + \cdots +w_mx_m = \sum^m_{i=0}w_ix_i
ここで、重み $w_0$ は $x_0=1$ として切片を表します。重回帰は、単回帰を複数の説明変数を扱扱えるように一般化したものであり、目的変数と複数の説明変数の関係を表すモデルの重みを学習することが目的です。
線形回帰モデル
scikit-learnで線形回帰をするには、linear_modelのLinearRegressionモデル(公式ドキュメント:http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html )を使います。主に利用するメソッドは以下の通りです。
- fitメソッド:線形モデルの重みを学習
- predictメソッド:線形モデルから目的変数を予測
- scoreメソッド:決定係数(線形モデルがどの程度目的変数を説明できるか)を出力
ここでは、UCI Machine Learning Repository (http://archive.ics.uci.edu/ml/index.php) で公開されている、ボストン市郊外の地域別住宅価格(https://archive.ics.uci.edu/ml/machine-learning-databases/housing/ )を使います。以下のコードでは、scikit-learnライブラリに付属のデータセットを読み込み、PandasのDataFrameに変換しています。(以降のコードの動作環境は、Python 3.7.3, pandas 0.24.2, scikit-learn 0.20.3 です。)
from sklearn.datasets import load_boston
boston = load_boston() # データセットの読み込み
import pandas as pd
boston_df = pd.DataFrame(boston.data, columns = boston.feature_names) # 説明変数(boston.data)をDataFrameに保存
boston_df['MEDV'] = boston.target # 目的変数(boston.target)もDataFrameに追加
データを覗いてみると、こんな感じです。
boston_df.head()

各変数(データ項目)の説明は以下の通りです。
| 変数 | 説明 |
|---|---|
| CRIM | 犯罪発生率 |
| ZN | 25,000平方フィート以上の住宅区画の割合 |
| INDUS | 非小売業種の土地面積の割合 |
| CHAS | チャールズ川沿いかを表すダミー変数 |
| NOX | 窒素酸化物の濃度 |
| RM | 平均部屋数 |
| AGE | 1940年より前に建てられた建物の割合 |
| DIS | 5つのボストンの雇用施設への重み付き距離 |
| RAD | 高速道路へのアクセスのしやすさ |
| TAX | 10,000ドルあたりの不動産税率 |
| PTRATIO | 生徒と教師の割合 |
| B | 黒人の割合 |
| LSTAT | 低所得者の割合 |
| MEDV | 住宅価格の中央値(1,000単位) |
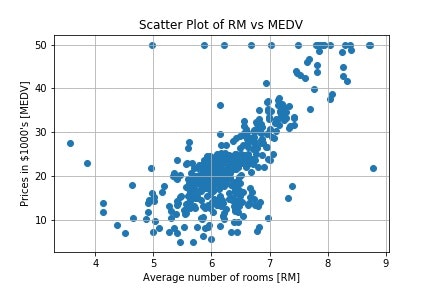
ここで、例えば以下のコードを使ってRM(平均部屋数)とMEDV(住宅価格)の関係を見てみると、おおむね線形関係にある、つまり平均部屋数が多いほど住宅価格も高いように見えます。
import matplotlib.pyplot as plt
%matplotlib inline
plt.scatter(boston_df['RM'], boston_df['MEDV']) # 平均部屋数と住宅価格の散布図をプロット
plt.title('Scatter Plot of RM vs MEDV') # 図のタイトル
plt.xlabel('Average number of rooms [RM]') # x軸のラベル
plt.ylabel('Prices in $1000\'s [MEDV]') # y軸のラベル
plt.grid() # グリッド線を表示
plt.show() # 図の表示
Pandasのcorr()メソッドで平均部屋数と住宅価格の相関係数を算出してみると、約0.7程度と正の相関があることがわかります。
boston_df[['RM','MEDV']].corr()

以降では、住宅価格(目的変数)と平均部屋数(説明変数)の関係を表現する線形回帰モデルを構築してみます。
線形回帰モデルの構築
fitメソッドで重みを学習することで、線形回帰モデルを構築します。学習の際には、説明変数Xと目的変数YにはNumpyの配列を利用するため、values属性で説明変数と目的変数の列からNumpyの配列を取り出しています。
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
X = boston_df[['RM']].values # 説明変数(Numpyの配列)
Y = boston_df['MEDV'].values # 目的変数(Numpyの配列)
lr.fit(X, Y) # 線形モデルの重みを学習
学習により得られた、線形モデルの切片 $w_0$ はintercept_属性に、説明変数の係数 $w_1$ はcoef_属性に格納されます。学習結果を確認すると、係数は約9.1、切片は約-34.7であることがわかります。
print('coefficient = ', lr.coef_[0]) # 説明変数の係数を出力
print('intercept = ', lr.intercept_) # 切片を出力
coefficient = 9.10210898118
intercept = -34.6706207764
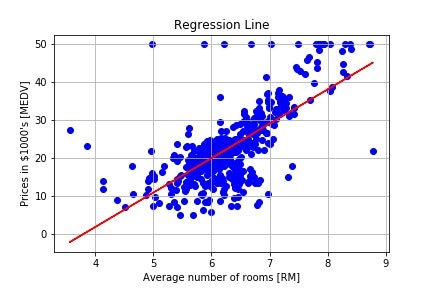
学習で得られた切片と係数を利用して、回帰直線を引いてみます。回帰直線をプロットするには、線形モデルに説明変数の値を与えたときの目的変数の値(予測値)が必要になります。以下のコードでは、これを得るためにpredictメソッドを利用しています。
plt.scatter(X, Y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
plt.plot(X, lr.predict(X), color = 'red') # 回帰直線をプロット
plt.title('Regression Line') # 図のタイトル
plt.xlabel('Average number of rooms [RM]') # x軸のラベル
plt.ylabel('Prices in $1000\'s [MEDV]') # y軸のラベル
plt.grid() # グリッド線を表示
plt.show() # 図の表示
与えられたデータ点にある程度フィットした回帰直線を引くことができていることが確認できます。
線形回帰モデルの性能評価
学習により得られた線形モデルの性能を評価するには、学習には用いていないデータでモデルを検証することが必要です。構築したモデルを今後利用する(例:売上予測モデルの予測結果を使ってビジネス計画を策定する・なんらかの施策を打っていく)ことを考慮すると、モデル構築時には得られない将来のデータに対して精度よく予測できることが重要であるためです。そのためには、まず手元のデータを学習データと検証データに分けます。そして、学習データでモデルを構築し、検証データを将来のデータと見立て、これに対するモデルの性能(汎化性能と呼ぶ)を評価します。
以下のコードでは、model_selectionのtrain_test_split(公式ドキュメント:http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html )を利用して、データを学習用と検証用に7:3の割合で分割し、学習データを用いて線形モデルを構築しています。
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, train_size = 0.7, test_size = 0.3, random_state = 0) # データを学習用と検証用に分割
lr = LinearRegression()
lr.fit(X_train, Y_train) # 線形モデルの重みを学習
線形回帰モデルの性能評価には、主に以下の方法・指標を利用します。
- 残差プロット:残差(目的変数の真値と予測値の差分)を可視化
- 平均二乗誤差:残差平方和をデータ数で正規化した値
- 決定係数:相関係数の二乗
残差プロットは、残差(目的変数の真値と予測値の差分)の分布を可視化したものです。線形モデルが目的変数を完璧に予測できる場合は残差は0となるので、予測精度の良い線形モデルの残差プロットは、0を中心にランダムにばらついたものになります。残差プロットに何かパターンが見られる場合は、線形モデルで説明しきれない情報があることが示唆されます。以下のコードは、残差プロットを描画します。
Y_pred = lr.predict(X_test) # 検証データを用いて目的変数を予測
plt.scatter(Y_pred, Y_pred - Y_test, color = 'blue') # 残差をプロット
plt.hlines(y = 0, xmin = -10, xmax = 50, color = 'black') # x軸に沿った直線をプロット
plt.title('Residual Plot') # 図のタイトル
plt.xlabel('Predicted Values') # x軸のラベル
plt.ylabel('Residuals') # y軸のラベル
plt.grid() # グリッド線を表示
plt.show() # 図の表示
残差プロットを見てみると、残差は0を中心に分布していますが、線形モデルで説明しきれないパターンもあるように見えます。
平均二乗誤差は、残差の平方和をデータ数で正規化したものであり、モデルの性能を数値化するのに役立ちます。もちろん、誤差が小さいほどモデルの性能は良いといえます。平均二乗誤差は、metricsのmean_squared_errorを利用することで算出できます。
from sklearn.metrics import mean_squared_error
Y_train_pred = lr.predict(X_train) # 学習データに対する目的変数を予測
print('MSE train data: ', mean_squared_error(Y_train, Y_train_pred)) # 学習データを用いたときの平均二乗誤差を出力
print('MSE test data: ', mean_squared_error(Y_test, Y_pred)) # 検証データを用いたときの平均二乗誤差を出力
学習データ、検証データそれぞれを用いたときの平均二乗誤差を比較すると、検証データを用いたときの誤差の方が大きいことがわかります。このことから、構築した線形モデルは学習データにフィットしすぎている(過学習と呼ぶ)ことが示唆されます。
MSE train data: 42.1576508631
MSE test data: 47.0330474798
決定係数も、線形モデルの予測誤差を反映した指標であり、値が大きいほど線形モデルがデータにフィットしているといえます。決定係数は、metricsのr2_scoreを利用することで算出できます。また、LinearRegressionモデルのscoreメソッドでも算出できます。
from sklearn.metrics import r2_score
print('r^2 train data: ', r2_score(Y_train, Y_train_pred))
print('r^2 test data: ', r2_score(Y_test, Y_pred))
学習データ、検証データそれぞれを用いたときの決定係数を比較すると、検証データを用いたときの決定係数の方が小さいことがわかります。このことからも、構築した線形モデルには過学習が起こっている可能性があることがわかります。
r^2 train data: 0.502649763004
r^2 test data: 0.435143648321
ここまでは単回帰のコード例を示してきましたが、重回帰の場合も簡単に試すことができます。
例えば、住宅価格(目的変数)と、平均部屋数および低所得者の割合(説明変数)の関係を表現する線形回帰モデルは、以下のようなコードで構築することができます。
lr = LinearRegression()
X = boston_df[['RM', 'LSTAT']].values # 説明変数(Numpyの配列)
Y = boston_df['MEDV'].values # 目的変数(Numpyの配列)
lr.fit(X, Y) # 線形モデルの重みを学習
おわりに
この記事では、scikit-learnライブラリで線形回帰をする方法について簡単に触れました。目的変数をより精度よく表現する線形モデルを構築するためには、特徴量(説明変数)選択や正則化を行うことを検討する必要がありますが、その点についても今後まとめてみようと思います。
参考
- [第2版]Python機械学習プログラミング 達人データサイエンティストによる理論と実装(https://www.amazon.co.jp/dp/B07BF5QZ41/ref=dp-kindle-redirect?_encoding=UTF8&btkr=1 )
更新履歴
- (2019/12/30)重回帰のコード例の追記