不均衡データとの向き合い方

ドコモ先進技術研究所アドベントカレンダー10日目の記事です。

ドコモの兼田と申します。この記事では、実際のデータ分析で直面しがちな不均衡データに関して、評価方法とモデル構築方法に関する基礎的な内容を説明します。また、記事の後半では、不均衡データに対する理解を深めるため、実験を行っています。至らない点も多々あるかと思いますが、よろしくお願いいたします。

1. 不均衡データとは

正例1％、負例99％ のようなデータです。二値分類に限らず、多クラス分類でも扱うことがあります。この記事では、最も一般的な二値分類（少数派の正例と多数派の負例が存在するケース）について主に説明します。

2. 評価方法

不均衡データからモデルを構築する上で重要なことは、モデルの評価方法を決めることです。評価方法が定まらなければ、目指すべきゴールが分からないことになります。不均衡データの場合は、通常時と同じようには解釈できない評価指標が存在するので注意が必要です。

どのように評価すべきか

結論としては、Precision-Recall曲線（以後、PR曲線）を描くことが良いと思います。その上で、各々の問題設定で求められるPrecisionとRecallのバランスを考慮し、適切な閾値を設定して最終的な二値分類を行うことが重要と考えます。モデルのパラメータチューニングを行う際には、PR曲線下の面積（以後、PR-AUC）を評価指標に使うと良いと思います。

以降は、不均衡データの予測において何故PR曲線やPR-AUCを使うべきかを説明します。

二値分類における正解と不正解

	Positive（予測）	Negative（予測）
Positive（真値）	TP: True Positive	FN:False Negative
Negative（真値）	FP: False Positive	TN: True Negative

この表は混合行列と言い、二値分類の評価指標を考える上で欠かせないものです。正例は正例と、負例は負例と予測することが正しいモデルであるため、TPとTNが多く、FNとFPが少ないモデルが良いモデルと言えます。

この時、誤った予測であるFNとFPのどちらを少なくすることを優先すべきかを考えます。一般的に不均衡データの予測の場合は、FNを減らすことを優先することが多いでしょうか。この理由は、少数派の正例を誤判定するくらいであれば、多数派の負例を正例と多少誤判定したとしても、正例は確実に正例と判定したいことが多いと考えられるためです（もちろん問題設定によります）。現在、自分が直面する問題設定では、FNとFPのどちらを優先すべきかを意識することは、最終的に二値分類を行う上で重要となります。

代表的な評価指標

上記を踏まえた上で、二値分類における代表的な評価指標を見てみましょう。

 Accuracy = (TP+TN)/(TP+FP+TN+FN)

Accuracyは、最も分かりやすい指標ですが、不均衡データの予測において採用することは難しいです。何故ならば、全て多数派の負例と予測するモデルを構築するだけで、Accuracyは簡単に最大値である1に近くなるためです。このようなモデルは、求めているモデルではないことは明らかなので、Accuracyを評価指標として用いることは不適切でしょう。

Precision = TP/(TP+FP)\\
Recall = TP/(TP+FN)

次に、PrecisionとRecallです。これらは一般的にトレードオフの関係にあるとされており、Precisionが高い/低い時、Recallは低く/高くなります。では、どちらを優先すべきかを考えるために、改めてFNとFPについて考えましょう。先ほど、不均衡データの予測ではFNを減らしたいことが多いと説明しましたが、その際には分母にFNが含まれるRecallを大きくすることを目指すべきでしょう。しかし、Recallを最大値の1にしたいだけであれば、Accuracyの例とは反対に全て少数派の正例と予測するモデルを構築すれば良いことになってしまいます。そのため、PrecisionとRecallのいずれかだけを評価指標とすることは無く、二つの評価指標から総合的にモデルを評価する必要があります。

とはいえ、PrecisionとRecallの二つの評価指標を一つにまとめたいことも多々あります。その際によく使われる評価指標が、次に紹介するF1値です。

F-measure = 2Recall*Precision/(Recall+Precision)

F1値は、PrecisionとRecallの調和平均から算出されます。直感的な理解としては、F1値が高いモデルは、PrecisionもRecallも高いモデルとなります。なお、F1値はPrecisonとRecallを等しく評価しており、PrecisionとRecallのいずれかを優先した指標ではないことに注意してください¹。

閾値について

次の評価指標の紹介に進む前に、二値分類における閾値の考え方について説明します。モデルが正例か負例かを予測する際には、まず「正例である確率80％」といったスコアが算出され、閾値（例えば50%）よりスコアが高ければ正例、低ければ負例とみなす処理が行われます。この閾値を変えることで予測結果も大きく変わるので、実際に二値分類を行う際には、どの閾値にすべきかを決める必要があります。

先ほど紹介した4種類の評価指標は、全て閾値を決定した上で算出される指標です。そのため、仮に「50%を閾値とする」と予め決まっていれば、閾値50%の時に算出されるF1値を最も高くするようにモデルを構築しても良いと思います。しかし、いずれかの閾値で適切に分類できれば良い（閾値を特定の値に定めない） ケースも多くあり、その際には閾値を必要としない評価指標を使うことになります。

閾値を必要としない評価指標

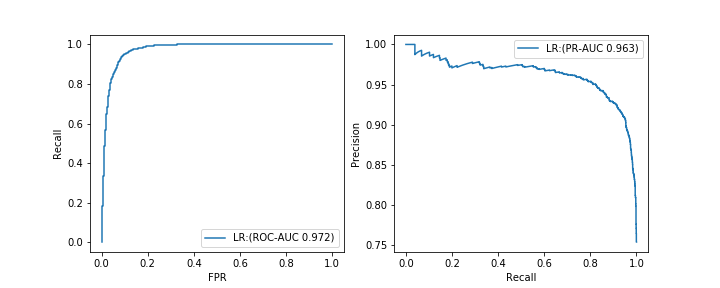
閾値を必要としない評価指標として、ROC曲線下の面積（ROC-AUC）と、PR曲線下の面積（PR-AUC）があります。

• ROC-AUC:閾値を変えながら、Recallと偽陽性率FPRの関係をプロットした時に描かれる曲線下の面積（左図）
• PR-AUC:閾値を変えながら、PrecisionとRecallの関係をプロットした時に描かれる曲線下の面積（右図）

なお、偽陽性率FPRの算出式は、下記の通りです。

FPR = FP/(FP+TN)

AUCというとROC-AUCを指すことが多いと思います。詳細な説明は割愛させていただきますが、いずれの指標も基本的な性質は似ており、最大値である1に近づくほど良いモデルとされています。また、どちらもF1値と同様に二つの評価指標を基に算出されるため、通常は、全てを正例もしくは負例と予測するような無意味なモデルを良いとみなすことはありません。しかし、不均衡データの予測の場合では、ROC-AUCが適切な評価指標とならない場合があります。

この理由の正確な説明が難しいのですが、自分なりの分かりやすい理解としては、ROC-AUCは「正例を正例と、負例を負例と正しく予測できているか」を評価ポイントとする一方で、PR-AUCは「正例を正例と正しく予測できているか」のみ評価ポイントとしているためです。 不均衡データの予測の場合、多数派である負例を負例と予測することは簡単であり、このことを評価ポイントとするROC-AUCは、ほとんどの正例を正例と予測できていないとしても、 大多数の負例を負例と予測するモデルを構築するだけで、最終的な値が高くなると考えられます。一方で、PR-AUCは、正例を正例と予測できているかだけを評価ポイントとするため、どれ程正しく負例を負例と予測しても全く評価されません。

ただし、PR-AUCがROC-AUCより優れているということではなく、不均衡データの予測においては、少数派である正例を適切に予測することを重要視する（ことが多いと考えられる）ため、PR-AUCが評価指標として適切だと考えられます。

なお実際には、PR-AUCが0.5のモデルAと、PR-AUCが0.4のモデルBがあった時に、「PR-AUCで見た全体の性能はモデルAの方が良いが、特定のRecallの時にはモデルBのPrecisionの方が高い」などということもあり得るので、あまりAUCという一つの値に固執せず、要求されるPrecisionとRecallのバランスを考慮し、PR曲線を描いて最終的なモデルの良し悪しを確認すると良いと思います。

3. モデル構築方法

以降は、不均衡データに対する一般的な対応策を紹介します。本記事では概要のみ簡単に紹介します。

データに対する処理

最も手軽な方法は、多数派データを減らす（アンダーサンプリング）、もしくは少数派データを増やす（オーバーサンプリング）ことです。これら二つを組み合わせることも考えられます。アンダーサンプリングをする際には、サンプリングの偏りを防ぐためにクラスタリングを用いる方法などがあります。また、オーバーサンプリングをする際には、SMOTEというアルゴリズムが有名です。

なお、サンプリングでデータを調整した場合、出力されるスコアの値が歪んでしまうので、スコアの値自体が重要な場合は、値の補正が必要となるそうです²。スコアの値自体は重要ではなく、正例か負例かに分けることが重要であれば、補正は不要と考えます。

アルゴリズムに対する処理

モデルを学習させる際には、内部的には目的関数の最小化問題を解いています。この時、多数派である負例を誤判定した時のペナルティと少数派である正例を誤判定した時のペナルティを調整することで、少数派である正例も正しく予測させることができます。

補足：アンサンブル学習の活用

アンダーサンプリングによって多数派である負例のデータを減らすとき、減らし方によっては負例のデータの傾向が変わることが想定されます。データの傾向を変えない工夫も多数ありますが、異なる対処の方法として、アンサンブル学習を組み合わせる手法が良いと言われています³。

補足：異常検知

あまりに正例と負例のデータ数に差がある場合は、少数派の正例を異常と見なした上で、異常検知のアルゴリズムを適用することも考えられます（本記事では割愛します）。

4. 実験

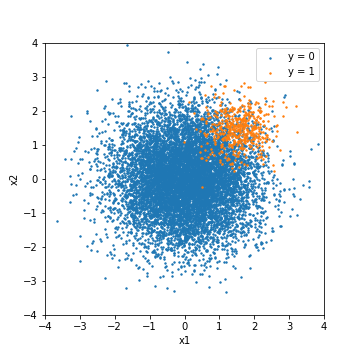
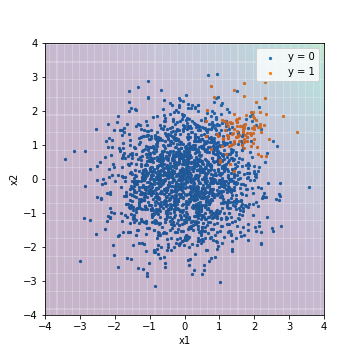
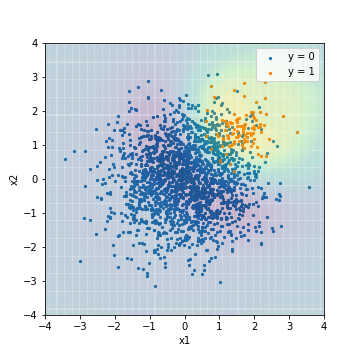
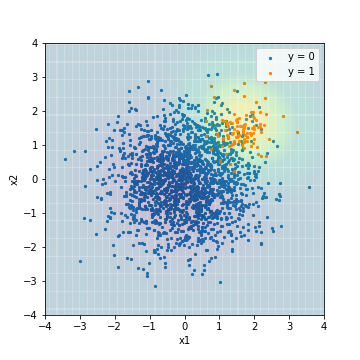
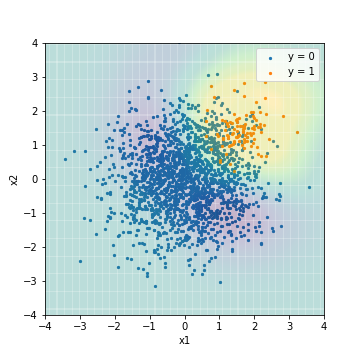
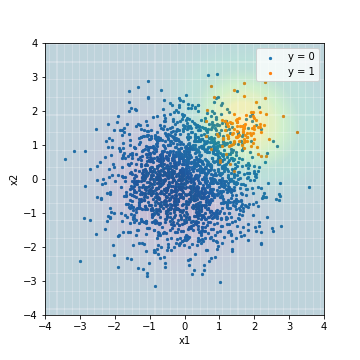
不均衡データに対する理解を深めるため、実験を行います。この実験では、正規分布に従う乱数から不均衡データを作成し、様々なモデルで評価を行います。データ量は、正例（y=1）が500件に対し、負例（y=0）が10000件です。可視化の容易さ重視のため、特徴量は二次元としています。

最低限の実験条件として、学習データとテストデータを8:2で分け、簡単にパラメータチューニングを行った後に、テストデータを予測しています。本実験では比較のため、F1値を基にチューニングした結果と、PR-ROC⁴を基にチューニングした結果をそれぞれ記載します。

# f1値でチューニングする場合
GridSearchCV(model, params, scoring="f1")
# PR-AUCでチューニングする場合
GridSearchCV(model, params, scoring="average_precision")

なお、データセットを分割する際には、正例と負例のバランスを維持したまま分割するようにしましょう⁵。

# scikit-learnのtrain_test_split関数を使う場合
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y)

ロジスティック回帰

対処無し

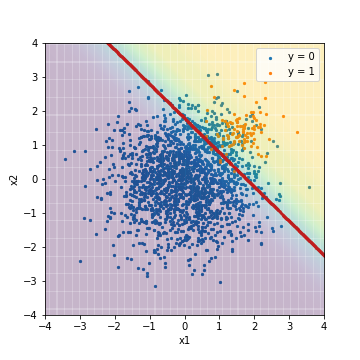
まずは、特別な工夫をしない通常のロジスティック回帰の予測結果です。

• F1値でチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
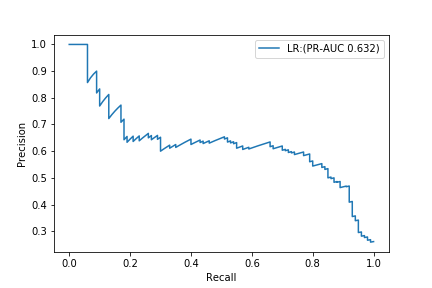
LR@F1	0.960	0.642	0.430	0.515	0.975	0.632

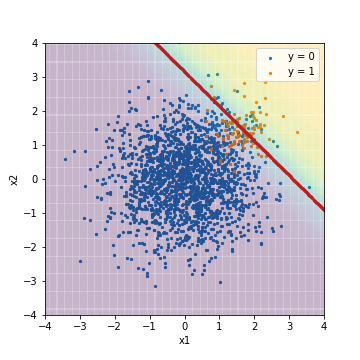
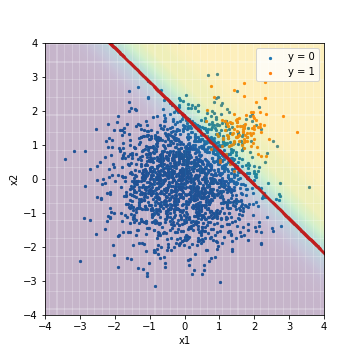
背景の色がスコアの値を示しており、黄色になるほど正例であることを、紫色になるほど負例であることを表しています。また、赤い線が閾値であり、Accuracy、Precision、Recall、F1値はこの閾値を基に分類した結果から算出されています。
結果は、予想通り多数派の負例に引きずられた結果となっています。

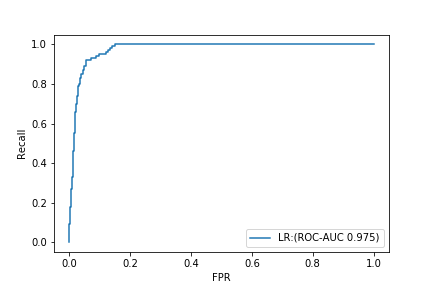
なお、ROC-AUCは、0.975という驚異的な数値になっています。

一方で、PR-AUCは0.632です。

ROC-AUCだけを見ると、恐ろしく良いモデルが出来たと思ってしまいますが、PR曲線を確認すると、あまり良いモデルとは言えないことが分かるかと思います。

• PR-AUCでチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
LR@PR-AUC	0.950	0.000	0.000	0.000	0.975	0.632

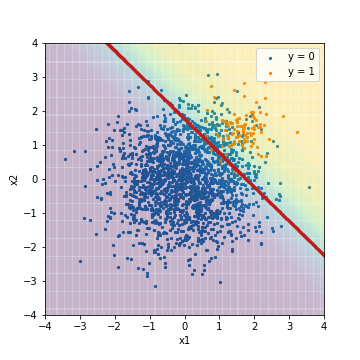
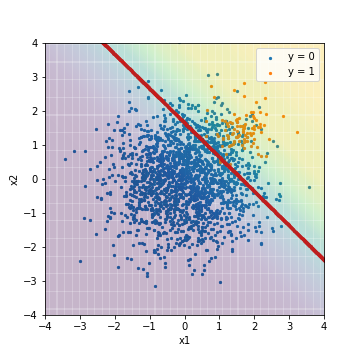
F1値でチューニングした結果と比べると、背景の色が全体的に紫になった（負例を指すようになった）ことが分かります。この結果では、全てのデータが閾値より下回っていることになり、閾値に基づく指標では全て負例と予測された上で値が算出されています。
一方で、ROC-AUCやPR-AUCの値は、F1値でチューニングした結果と変わりません。これは、ROC-AUCやPR-AUCがスコアの絶対値ではなく、スコア順に予測結果を並び替えた時に上位に正例が、下位に負例が集まっているかで評価する指標であるためです。言い換えると、この二種類の結果は、スコアの絶対値は変わっているものの、スコア順に予測結果を並び替えた時の順序はほぼ同じであると推察できます。

アルゴリズムに対する処理

次に、アルゴリズムに対する処理を適用したロジスティック回帰の結果です。scikit-learnでは、class_weightパラメータを設定するだけで良いです。

# アルゴリズムに対する処理を適用する場合
clf = LogisticRegression(class_weight="balanced")

• F1値でチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
LR_weight@F1	0.901	0.329	0.950	0.488	0.975	0.633

• PR-AUCでチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
LR_weight@PR-AUC	0.887	0.301	0.950	0.457	0.975	0.631

先ほどF1値でチューニングした通常のロジスティック回帰の結果と比べると、閾値の場所が正例を正しく予測しようと左下へ大きく動いていることが分かります。これに伴い、Recallが急激に高くなっています。一方で、ROC-AUCやPR-AUCは、やはりあまり変わりません。こちらに関しても、通常のロジスティック回帰の時と同様に、スコア順に予測結果を並び替えた時の順序は変わっていないと考えられます。

データに対する処理

最後に、データに対する処理を適用したロジスティック回帰の結果です。不均衡データ予測のライブラリであるimbalanced-learnに実装されているSMOTETomekという手法を用います。こちらは、アンダーサンプリングとダウンサンプリングを組み合わせた手法となります。SMOTETomekの適用で、元々正例400件、負例7600件だった学習データが、正例負例共に7439件となります。

• F1値でチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
LR_sampling@F1	0.891	0.308	0.950	0.466	0.975	0.632

• PR-AUCでチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
LR_sampling@PR-AUC	0.873	0.279	0.970	0.433	0.975	0.632

アルゴリズムに対する処理を適用したロジスティック回帰の結果とほぼ同じ結果となりました。各指標とも大きな差はありません。

ロジスティック回帰の結果は、以下の通りとなりました。今回の例では、PR-AUCという観点で評価すると、どのモデルも同様の性能であることが分かります。

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
LR@F1	0.960	0.642	0.430	0.515	0.975	0.632
LR@PR-AUC	0.950	0.000	0.000	0.000	0.975	0.632
LR_weight@F1	0.901	0.329	0.950	0.488	0.975	0.633
LR_weight@PR-AUC	0.887	0.301	0.950	0.457	0.975	0.631
LR_sampling@F1	0.891	0.308	0.950	0.466	0.975	0.632
LR_sampling@PR-AUC	0.873	0.279	0.970	0.433	0.975	0.632

SVM(RBFカーネル)の場合

次に、非線形モデルのSVM（RBFカーネル）で同様の比較を行ってみました。なお、こちらは閾値の赤線は記載していません。

対処無し

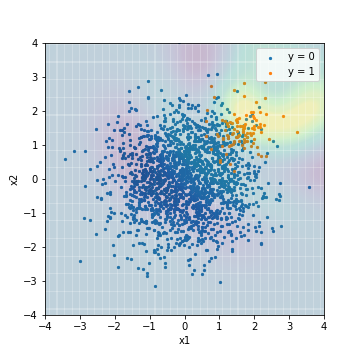
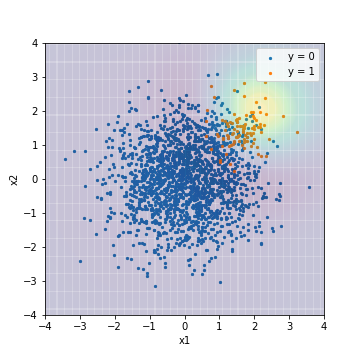
まずは、特別な工夫をしない通常のSVMの予測結果です。

• F1値でチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
SVM@F1	0.964	0.656	0.590	0.621	0.966	0.629

• PR-AUCでチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
SVM@PR-AUC	0.950	0.000	0.000	0.000	0.934	0.650

ロジスティック回帰の結果と異なり、F1値でチューニングするか、PR-AUCでチューニングするかで結果に明確な違いが出ています。PR-AUCでチューニングした際のスコアは、正例の中心よりやや右上から放射状にスコアが小さくなるように予測されており、不均衡データに対する対処をしていないこのモデルでは妥当な結果に見えます。反対に、F1値でチューニングした際のスコアは、若干不自然な結果に見えます。**実際にPR-AUCでチューニングしたSVMは、ロジスティック回帰の全てのモデルよりPR-AUCが高く、反対にF1値でチューニングしたSVMは、ロジスティック回帰の全てのモデルよりPR-AUCが低くなっています。**このことを踏まえると、表現力が豊かなモデルを構築する時こそ、チューニング時の評価指標が重要になると考えられます。

アルゴリズムに対する処理

次に、アルゴリズムに対して調整を行ったSVMの結果です。

clf = SVC(class_weight="balanced")

• F1値でチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
SVM_weight@F1	0.904	0.339	0.970	0.503	0.976	0.575

• PR-AUCでチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
SVM_weight@PR-AUC	0.050	0.050	1.00	0.095	0.978	0.639

いずれの結果においても、通常時のSVMの予測結果と比べ、より正例を正しく予測しようとモデルが学習されていることが分かります。一方で、F1値でチューニングしたSVMのPR-AUCは、0.575と今までで一番悪くなってしまいました。

データに対する処理

最後に、データに対する処理を適用したSVMの結果です。

• F1値でチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
SVM_sampling@F1	0.903	0.338	0.990	0.504	0.968	0.473

• PR-AUCでチューニング

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
SVM_sampling@PR-AUC	0.877	0.289	1.0	0.448	0.978	0.637

全体的な傾向としては、アルゴリズムに対する処理を適用したSVMの結果と似たような結果となりました。一方で、F1値でチューニングしたモデルのPR-AUCは、0.473と更に悪くなってしまいました。

SVMの結果は、以下の通りとなりました。今回の例では、PR-AUCという観点で評価すると、チューニングする際の評価指標にPR-AUCを設定しないと、大きく性能が下がることが分かりました。これは、SVMは表現力の高いモデルであるため、ロジスティック回帰のような線形モデルと比べ、チューニングに用いた評価指標に特化したモデルになるからと考えられます。

	Accuacy	Precision	Recall	F1	ROC-AUC	PR-AUC
SVM@F1	0.964	0.656	0.590	0.621	0.966	0.629
SVM@PR-AUC	0.950	0.000	0.000	0.000	0.934	0.650
SVM_weight@F1	0.904	0.339	0.970	0.503	0.976	0.575
SVM_weight@PR-AUC	0.050	0.050	1.00	0.095	0.978	0.639
SVM_sampling@F1	0.903	0.338	0.990	0.504	0.968	0.473
SVM_sampling@PR-AUC	0.877	0.289	1.0	0.448	0.978	0.637

PR曲線比較

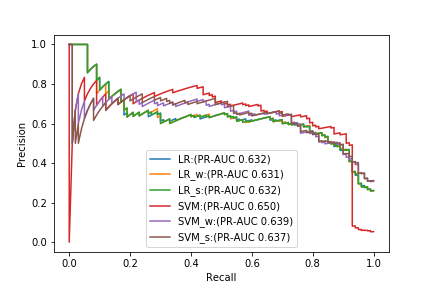
最後に、今回の実験で試した6種類のモデル（PR-AUCでチューニング）のPR曲線を並べました。

PR-AUCだけで比較すると、最も良いモデルは何も対処をしない通常のSVMですが、Recallが高い時には、SVMのPrecisionが急激に下がっており、他のモデルを使う方が良い結果となっています。この結果からも、PR-AUCだけで適切なモデルを選択することは難しいということが分かるかと思います。繰り返しになりますが、PR曲線からPrecisionとRecallのバランスを考慮し、その問題設定にとって最も性能の良いモデルを見つけることが重要だと思います。

まとめ

• PR曲線を描いてみよう!

参考

• 不均衡データ - ROC曲線欠点の実装例
• インバランスデータにおけるPR曲線とROC曲線の振る舞いの違い
• ゼロからわかる機械学習の評価指標！適合率-再現率／ROC曲線とAUC
• ROC曲線とPR曲線の違いについての考察

1. F1値を一般化したFβ値という指標もあります。βの値を調整することで、PrecisionとRecallの優先度合いを調整することができます。 ↩

2. ダウンサンプリングによる予測確率のバイアス ↩

3. 不均衡データ予測のライブラリであるimbalanced-learnには、この方法を実装するために、BalancedBaggingClassifierという便利なクラスが用意されています。 ↩

4. scoringパラメータに指定しているAverage PrecisionはPR-ROCの近似値になります。参考：https://scikit-learn.org/stable/modules/generated/sklearn.metrics.average_precision_score.html ↩

5. GridSearchCVは二値分類の場合デフォルトで層別に（バランスを維持したまま）分割されます。 ↩