はじめに
機械学習の分類タスクでは,アルゴリズムの性能を測るために "ROC曲線" や "Precision-Recall曲線(以下,PR曲線)"の下面積(以下,AUC)を使います.
個人的には正直あまり区別してこなかったのですが,@ogamiki さんのこちらの記事にはその使い分けのヒントが書いてありました.
TNの値が大きくなりやすい場合や、ネガティブケースが豊富な場合には、PR曲線が一般的に適しています。
このケースではPR曲線のほうがより違いをはっきりと表現することができます。
どんな理屈でそうなるのか少し気になったので,考察してみました.
ROC曲線やPR曲線とは
ROC曲線やPR曲線については,まずはこちらの記事をご覧ください.
ROC曲線やPR曲線は,「テストサンプルをポジティブだと予測される順にランキングしたとき,実際に上位にポジティブなサンプルを固められたか」という,ランキングの正確さを表す指標と見ることができます.
| ランキング | 真実 |
|---|---|
| 1 | 1=ポジティブ |
| 2 | 0=ネガティブ |
| 3 | 1 |
| 4 | 1 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
例えばこのようなランキングでは,本来ネガティブなサンプルが一つ2位に位置しており,他のポジティブなサンプルよりも上位になってしまっているという予測のミスが発生しています.
このランキングが得られたとき,各順位までのTPRやFPR,もしくはPrecisionやRecallを求めます.
| ランキング | 真実 | TPR=Recall | FPR | Precision |
|---|---|---|---|---|
| 1 | 1=ポジティブ | 1/3=0.333 | 0/4=0.000 | 1/1=1.000 |
| 2 | 0=ネガティブ | 1/3=0.333 | 1/4=0.250 | 1/2=0.500 |
| 3 | 1 | 0.666 | 0.250 | 0.666 |
| 4 | 1 | 1.000 | 0.250 | 0.750 |
| 5 | 0 | 1.000 | 0.250 | 0.600 |
| 6 | 0 | 1.000 | 0.250 | 0.500 |
| 7 | 0 | 1.000 | 0.250 | 0.286 |
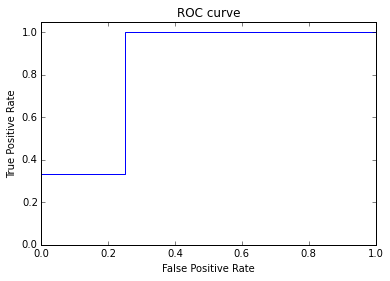
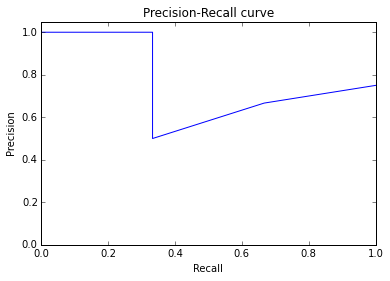
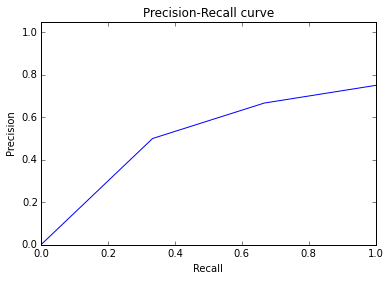
ROC曲線ならFPRを横軸,TPRを縦軸に,PR曲線ならRecallを横軸に,Precisionを縦軸にして,ランキング上位から順に折れ線で描きます.
ROC曲線とPR曲線の違いに関する私の結論
ROC曲線とPR曲線の違いに関して,先に私の結論を述べてしまうと次の通りです.
- PR曲線のAUCの方が「ランキングが上位のサンプルの予測の正確さ」をより重視するのに対し,逆にROC曲線のAUCは「ランキング全体に渡る正確さ」を満遍なく評価している
直感的には,PR曲線のAUCの方がランキング上位の精度を 虫眼鏡で拡大して見ている というイメージです.
このことから,次のような示唆も得られます.
- ランキングの上位の正確さをより重視して測定したいならPR曲線のAUCを採用すべき
- 「ネガティブケースが豊富な場合には、PR曲線が適している」という説は,「ネガティブケースが豊富な場合にはよりランキング上位を重視したくなる人間の性」から由来している
- しかしPR曲線のAUCはランキング上位のごくわずかなテストサンプルの違いで大きく変動するため,信頼性には疑問が残る
定性的な解説
ROC曲線とPR曲線の違いを考察するヒントは,ROC曲線もPR曲線も両方TPR=Recallの軸を共有しているということです.
ただし,TPR=Recall軸はROC曲線では縦軸に,PR曲線では横軸に置かれます.ここがミソだと思います.
例えば先の例で,TPRが0.666に到達した時点(ランキング3位)を考えてみましょう.
| ランキング | 真実 | TPR=Recall | FPR | Precision |
|---|---|---|---|---|
| 1 | 1=ポジティブ | 1/3=0.333 | 0/4=0.000 | 1/1=1.000 |
| 2 | 0=ネガティブ | 1/3=0.333 | 1/4=0.250 | 1/2=0.500 |
| 3 | 1 | 0.666 | 0.250 | 0.666 |
| 4 | 1 | 1.000 | 0.250 | 0.750 |
| 5 | 0 | 1.000 | 0.250 | 0.600 |
| 6 | 0 | 1.000 | 0.250 | 0.500 |
| 7 | 0 | 1.000 | 0.250 | 0.286 |
TPRが0.666に達した時点では,ROC曲線では(0.250,0.666)という座標に位置し,そこまででは全体の面積のうちせいぜい1/4しか担当していません.
したがって,(0.250,0.666)に至る手前でどれだけ下手な予測をしても,AUCへの影響は小さいもので済みます.
一方PR曲線では(0.666,0.666)という座標に位置し,その座標まででなんと全体のAUCの2/3を担当しています.
ですので,(0.666,0.666)に至る手前で下手をこいてしまうと,ROC曲線に比べて8/3倍もの影響力があります.
実際,1位と2位を入れ替えたときのROC曲線とPR曲線のAUCは次のとおりです.
実験的検証
論より証拠,実験で示してみました.
実験手順は以下のとおりです.
- 使用したプログラムはPythonで,テストデータとしてscikit-learnにデフォルトで入っている,"boston house-prices dataset"を使いました.
- 検証プログラム全体はこちら(GitHub)
- このデータセットは全体で506サンプルで,このうち84サンプル(17%)が30ドル以上の物件,残りが30ドル未満の物件で,それぞれをポジティブ・ネガティブとラベル付けしました.
- このポジ・ネガを改めて説明変数だけから予測するモデルを立て(モデルはロジスティック回帰モデルです),予測スコア順にランキングを作りました.
- このランキングから作られるROC曲線のAUCは0.985, PR曲線は0.928です(学習に使ったデータ自身を予測に使っているのでかなり高い性能です).
- ここで予測スコアのランキングを0~100位まで一部だけを,ランダムにシャッフルした新しいランキングを作り,同じようにROCやPR曲線のAUCを計算します
- 新しいランキングでは0~100位までの順位が完全にアトランダムになってしまっているため,AUCは元より劣化するはずです
- 実際には確率的ゆらぎを抑えるため,10回シャッフルしてAUCを計算した平均をとっています.
- 同じように元のランキングの5位~105位まで,10位~110位まで,...と言った具合に,一部の順位をシャッフルしなおしたランキングに対してAUC(の平均)を計算していきます.
仮説が正しければ,PR-AUCの方がROC-AUCに比べて,より上位のランキングをシャッフルしたときのAUCの劣化が激しいはずです.
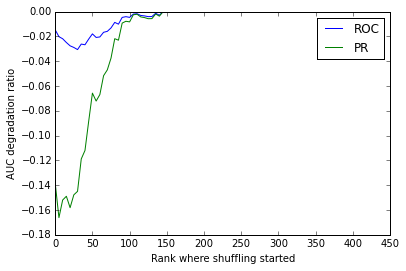
検証結果が次の図です.
横軸がランキング中どの順位からシャッフルをスタートさせたか,縦軸は元のAUCの値に対して何割劣化したかを表します.
仮説通り,PR-AUCの方が(最大16%劣化)ROC-AUC(最大3%劣化)に比べて,より上位のランキングでシャッフルされたときに(つまりグラフの左側で)大きくAUCが劣化しています.
逆に言えば,より上位のランキングで正確に予測することができれば,PR-AUCはROC-AUCよりも飛躍的に向上する,ということを示唆しています.
結論と感想
以上の検証結果から改めて結論を繰り返すと,
- PR曲線のAUCの方が「ランキングが上位のサンプルの予測の正確さ」をより重視するのに対し,逆にROC曲線のAUCは「ランキング全体に渡る正確さ」を満遍なく評価している
というような結論を得て,私自身は納得感を得ることができました.
一方で,@ogamiki さんのこちらの記事のコメントにも書かせていただいたよいに,実用的な側面ではROC曲線とPR曲線でまた違ったメリット・デメリットもあります.
(以下,引用)
1. 軸の解釈性
まずPrecision-Recallは,軸の解釈が互いにトレードオフの関係にあって,統計に詳しくない人にも理解してもらいやすい です.
例えば全顧客の中から優先してアプローチすべき優良顧客を判定する問題だと,
「Precisionが高いけどRecallが低い」=「無駄は少ないが,取りこぼしの多い判定になっている=機会損失が起きている」
「Precisionが低いけどRecallが高い」=「取りこぼしが少ないが,無駄撃ちが多い判定になっている=アプローチの予算が無駄になる可能性が高い」
というように,PR曲線を囲みながらビジネスの言葉で語り合うことができます.
逆にROCの場合FPRが特に理解しづらく,どれだけ説明してもなかなかわかってもらえない経験が多いです.結局は「とりあえず精度を測定するための図で,左上に寄っていると嬉しい図だと覚えてください」というレベルの理解で落ち着くため,意思決定者の納得度はPR曲線に及ばないと思います.
2. 絶対水準の解釈性
一方ROCはPR曲線に比べて,AUCの絶対水準に明確な意味を持たせやすい という利点があると思っています.
どんな予測問題でも,ROC-AUCは最大値が1で,ランダム予測の場合0.5をとります.一方でPR曲線は最大値が1なのは変わらないのですが,ランダム予測がどの値になるかは問題の正例と負例の割合によって異なりますよね.
"ROC-AUCで0.9が出ました!" と言われればどんな問題であっても「それは良い予測ができたね」と言えるのですが,"PR-AUCで0.4が出ました!" と言われたときにそれがどのくらいすごいことなのか,もう少し情報がないとなかなか判断が難しいと思います.
そういう意味で,「この予測で十分な精度が出ているのか」を短い時間で判断しなくてはならないような現場では,ROC曲線の方が共通言語として適していると思います.
(引用ここまで)
分類の精度として何を共通言語として採用するかは,どのアルゴリズムを使うか以上に大切ではないでしょうか.
この記事で少しでも分析の現場で戦う方々の納得感が高まれば幸いです.