対象者
最適化手法ごとの比較を見てみたい人へ。
ここで紹介している手法をいろいろな探索空間で比較してみます。
他にいい探索平面をお持ちの方や、試してみて欲しい探索空間がある方は情報をお待ちしています。
更新履歴
- 2021/1/3
- 実験コードを刷新しました。それに伴いグラフを追加した部分があります。
- 探索平面を追加しました。
目次
- x^2-y^2
- y^2-x^2
- tanh(x)^2+tanh(y)^2
- -sin(x)/x-sin(y)/y+(x^2+y^2)/7
- -sin(x)/x-sin(y)/y+(x^2+y^2)/10
- tanh(x)^2+(x^2+y^2)/8
- 高画質版
- 使用したコード
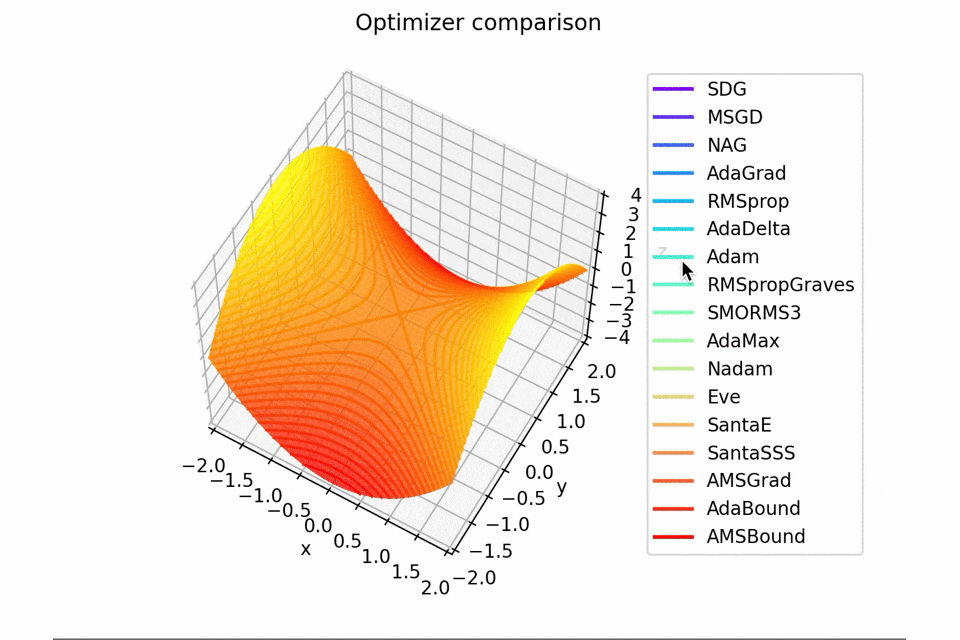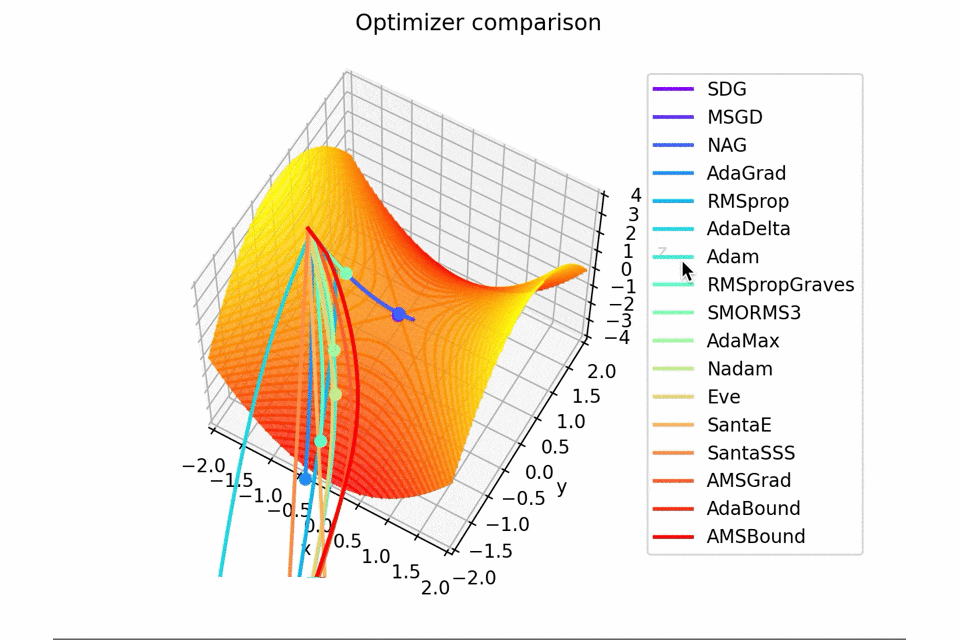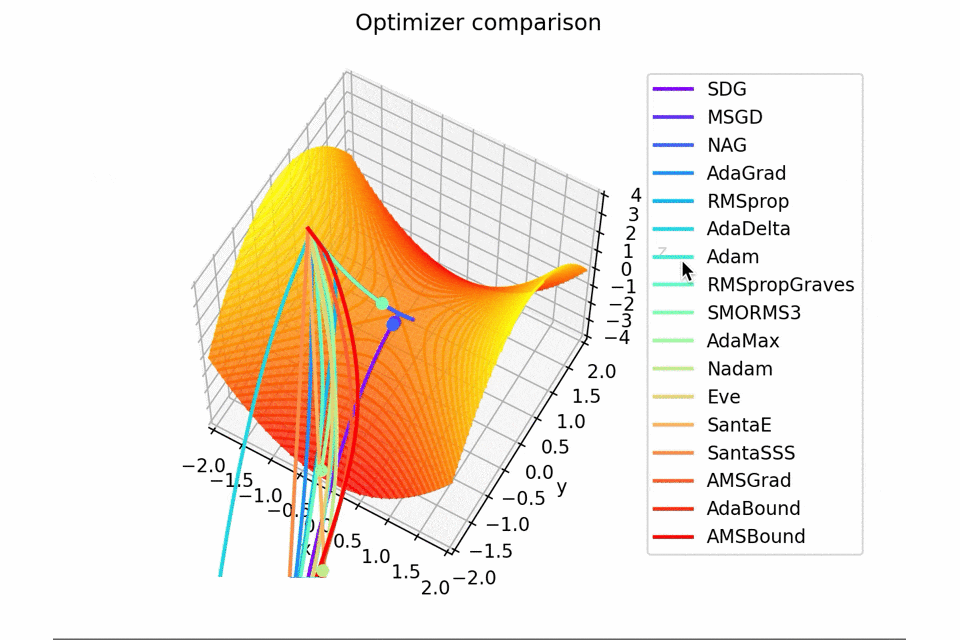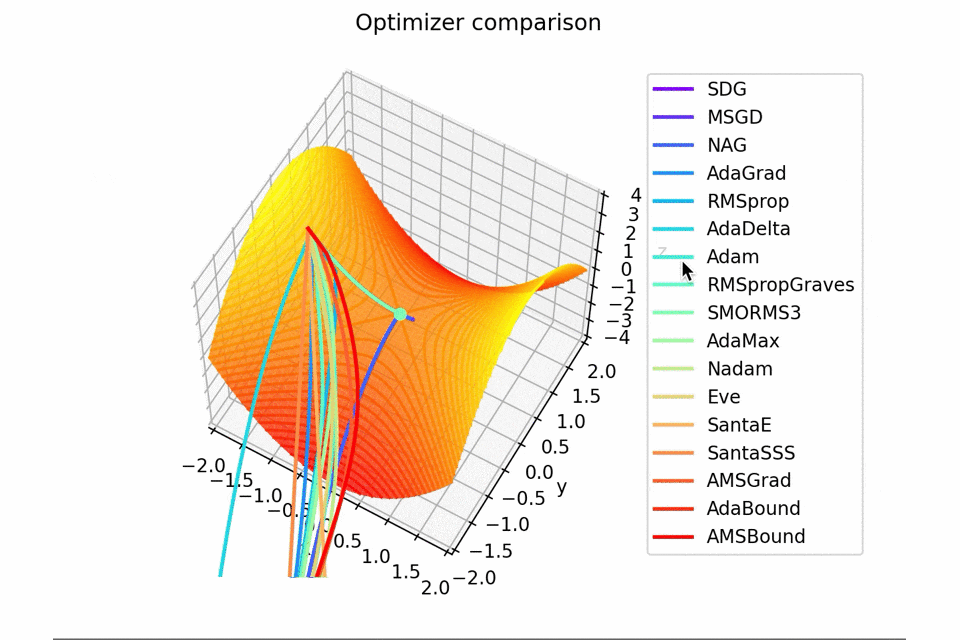
x^2-y^2
とりあえず
f(x, y) = x^2 - y^2
で、原点周辺を探索させみます。
初期位置は$(x_0, y_0) = (-1.5, 10^{-4})$としています。$y$座標が0でないのは学習則において傾きが完全に$0$になることを想定していない物が含まれているためです。
まあ普通は勾配が完全に$0$なることはないと言っていいので問題ないですね。
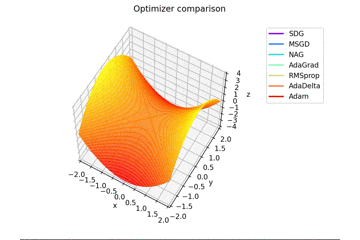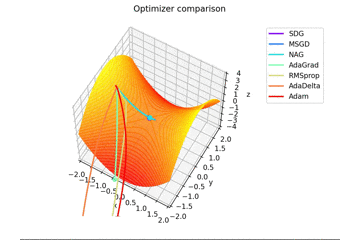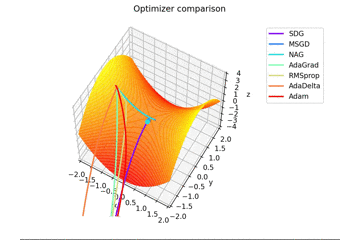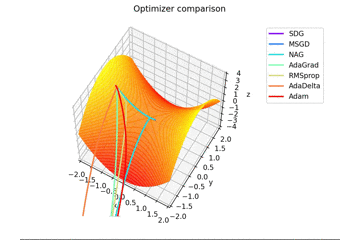
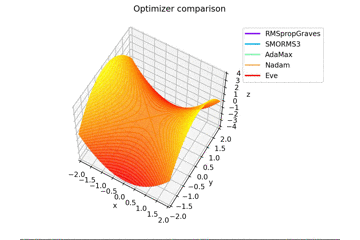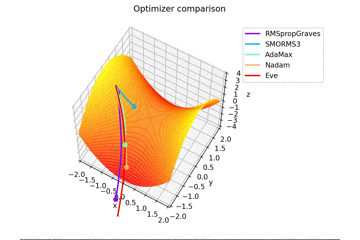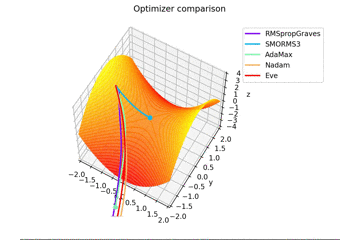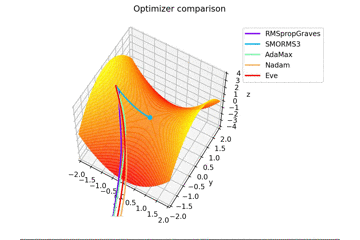
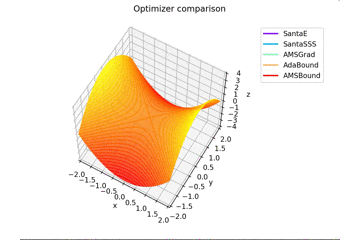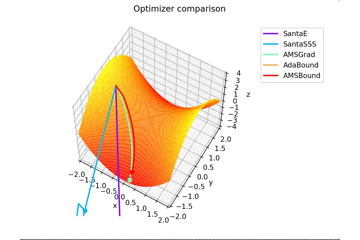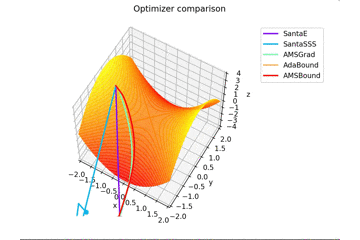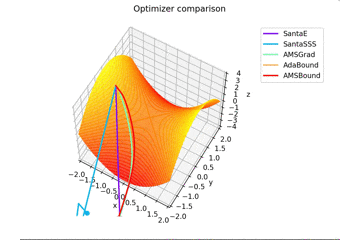
少し$y$軸方向の勾配があるため鞍点に捕まらない学習則が多いですね。捕まる学習則も最終的には落ちていきます。
ちなみに完全にゼロだとこんな感じです。
Santaは一瞬で蒸発し、また勾配が完全にゼロでも問題ない学習則は鞍点に完全に捕まります。SMORMS3はもはやピクリとも動きません。コードにミスがあるのかもしれません...
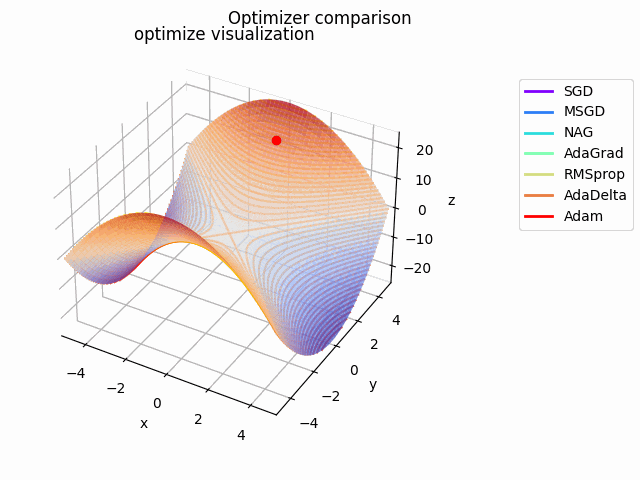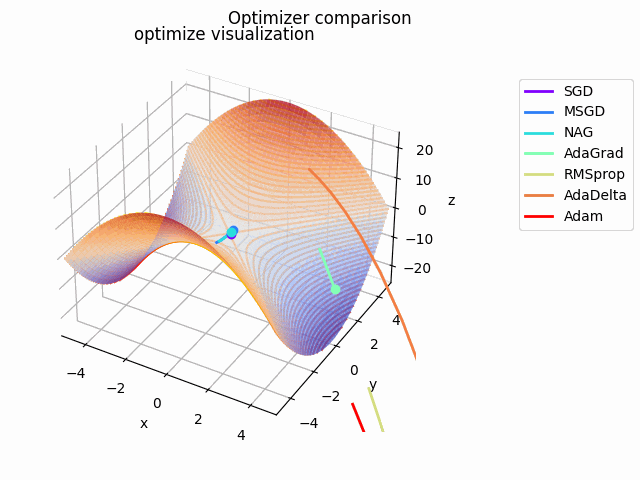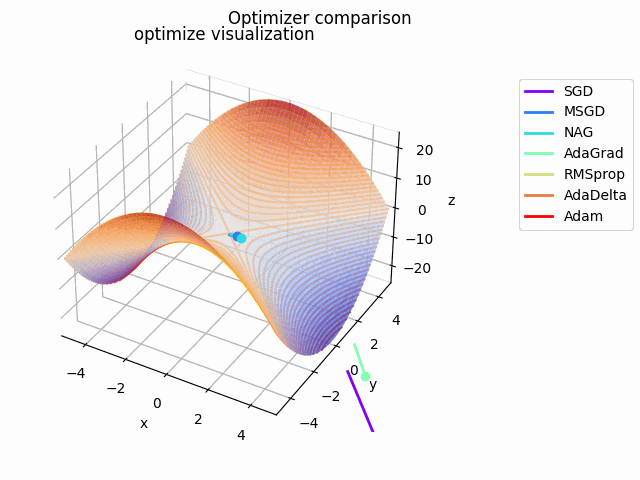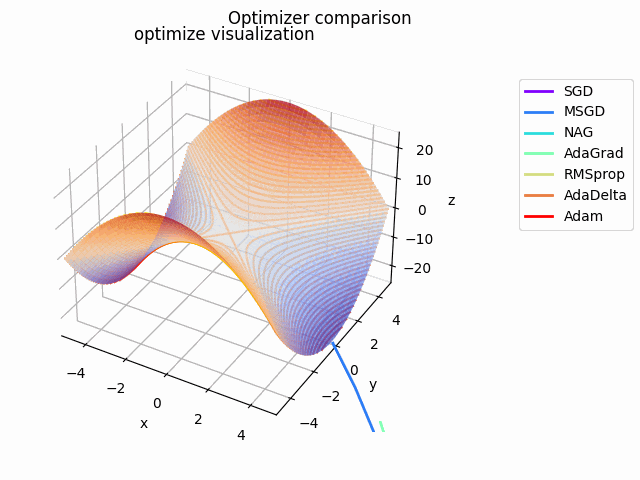
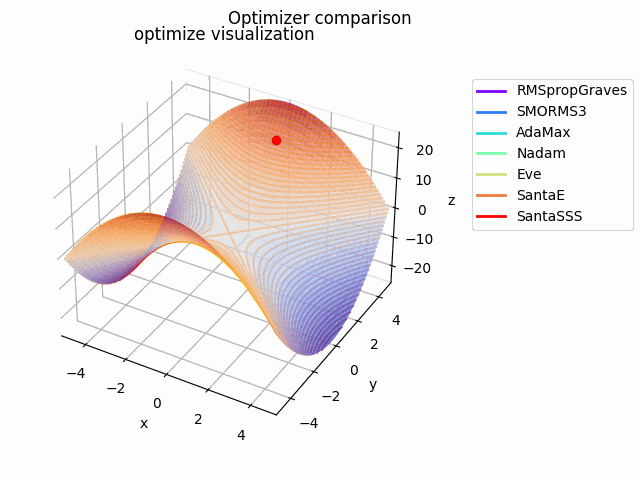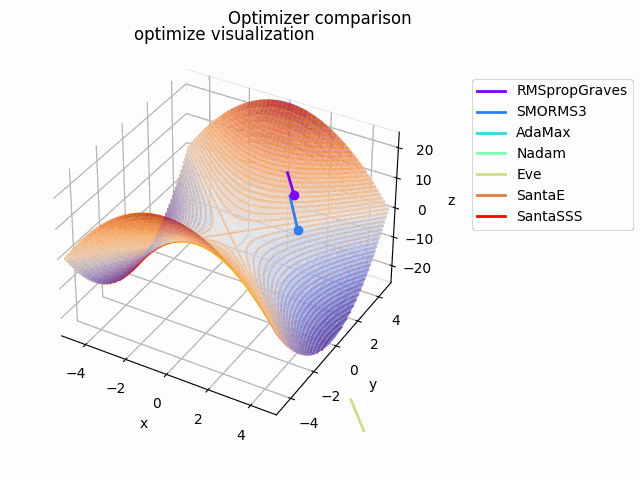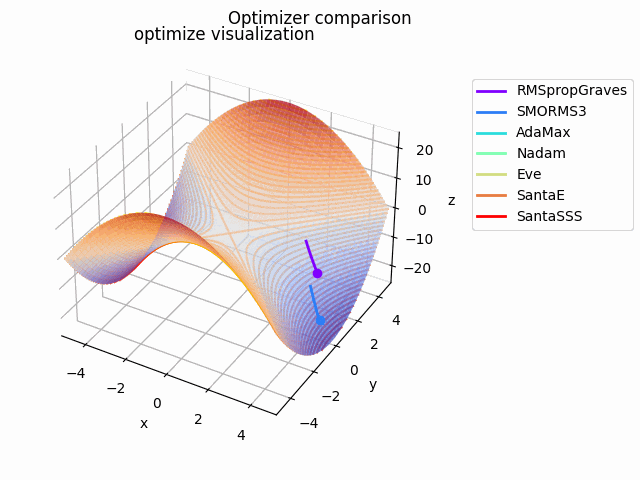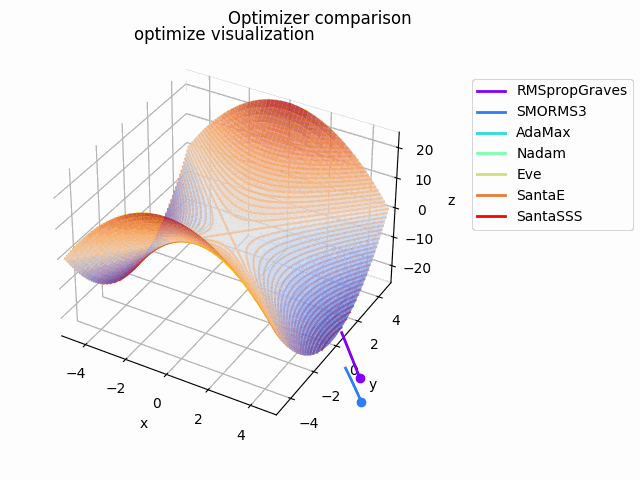
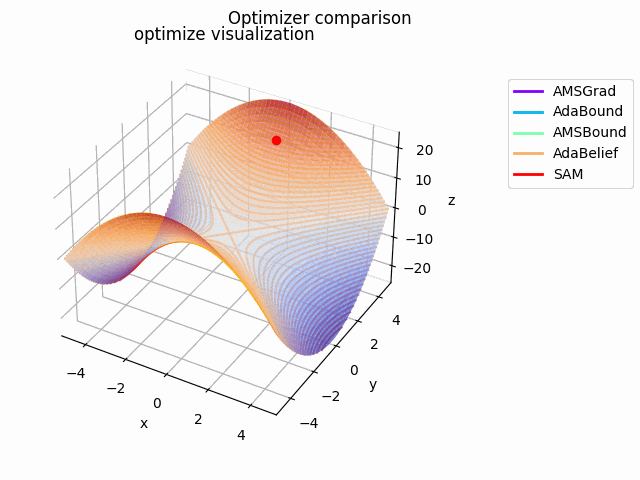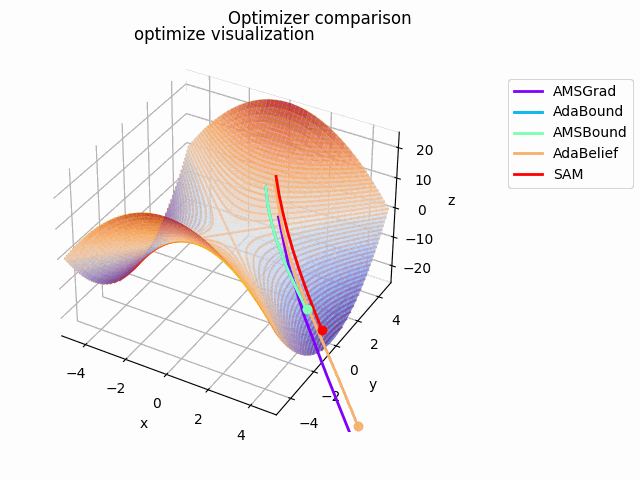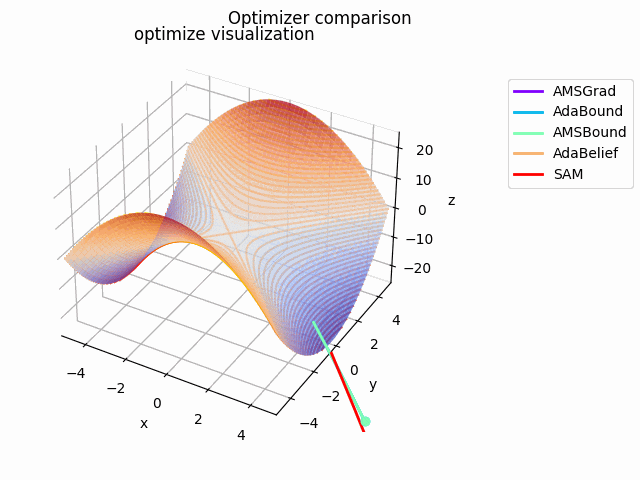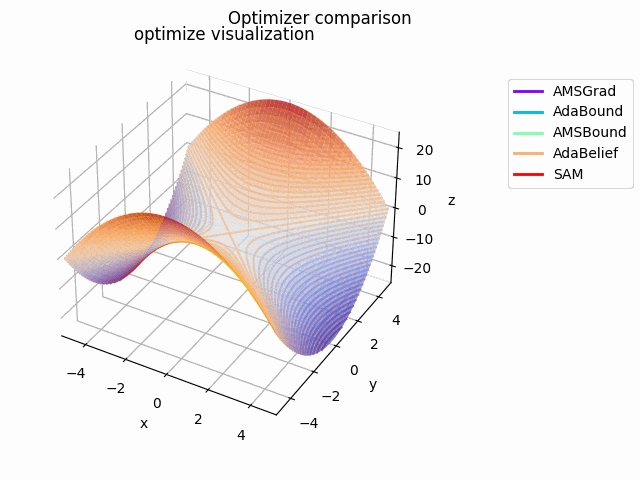
y^2-x^2
2021/1/3に追加しました。
実験コード刷新に伴って実験し直したものになります。見やすさのために$y^2-x^2$としてあります。別にそうせずともグラフを回せばいいことに気づいたのは後になってからでした...
初期値は$(x_0, y_0) = (10^{-4}, 4)$で、ハイパーパラメータは実験コードにある通りの値を使用しています。
tanh(x)^2+tanh(y)^2
続いては
f(x, y) = \tanh^2 x + \tanh^2 y
で、初期位置$(x, y) = (-1, 2)$で試しました。
やはりSMORMS3だけ鞍点に嵌まりますね...
Santaはどこかへ行ってしまっていますが、一応戻ってくる様子が見えますね。
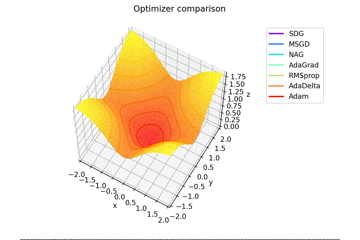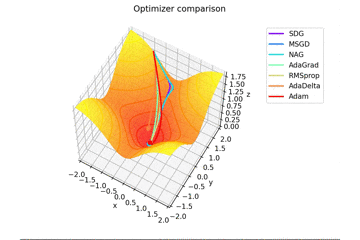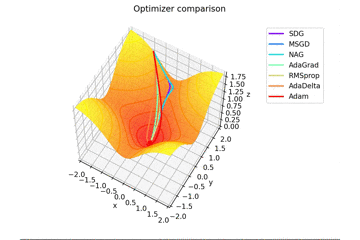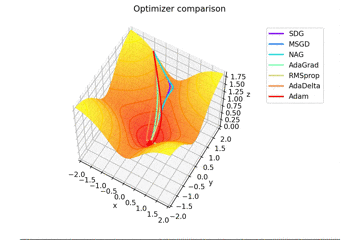
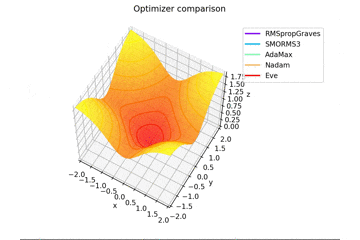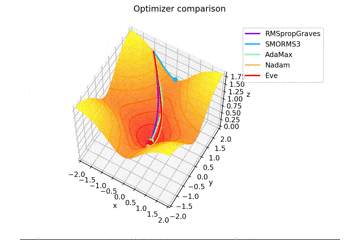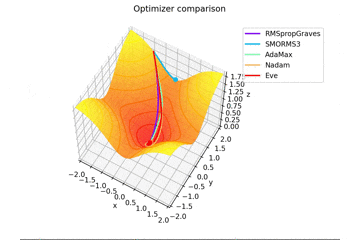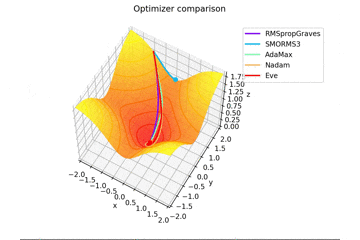
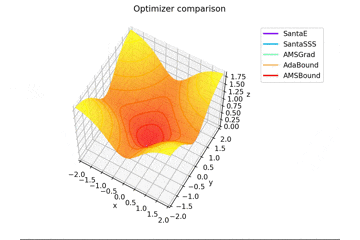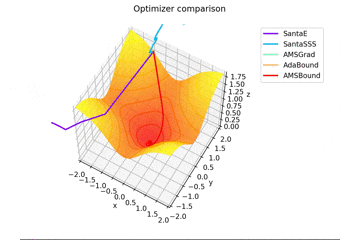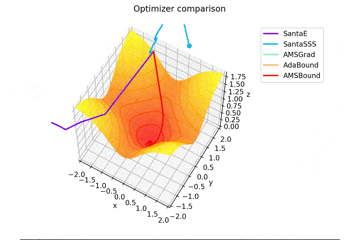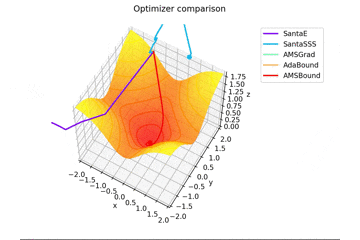
2021/1/3追加
グラフを追加しました。
うまく動作していなかったSMORMS3もしっかり動いてますね。よかったよかった。
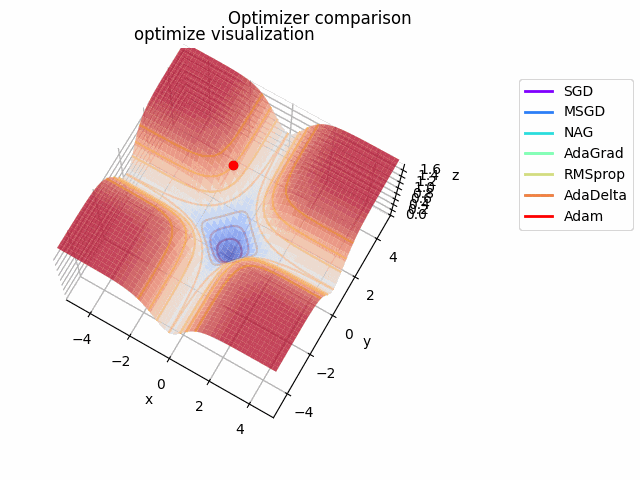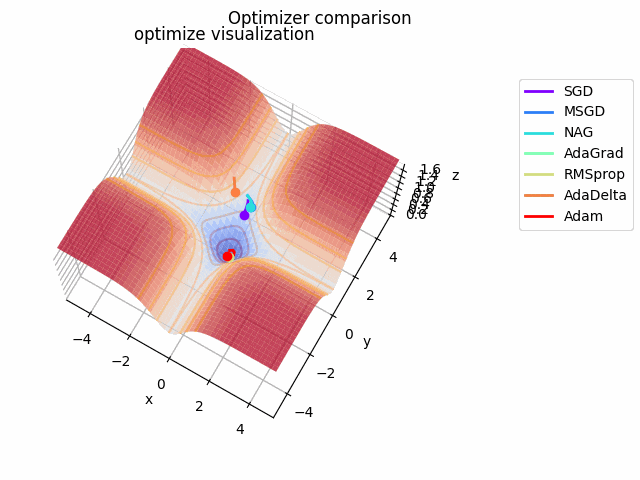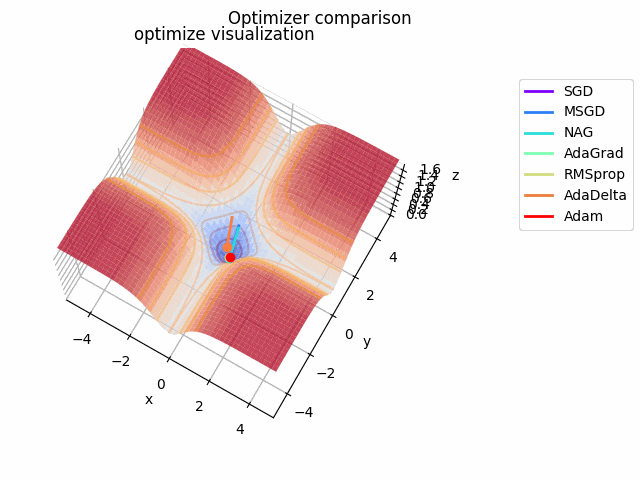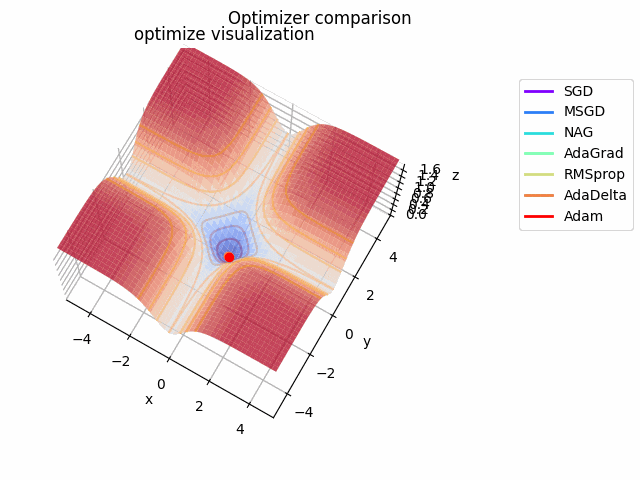
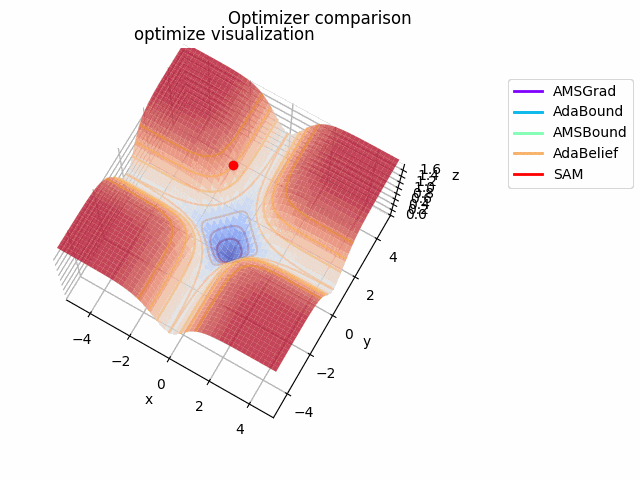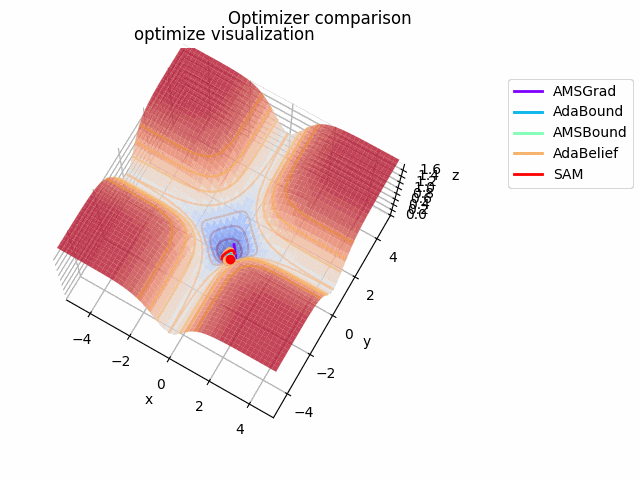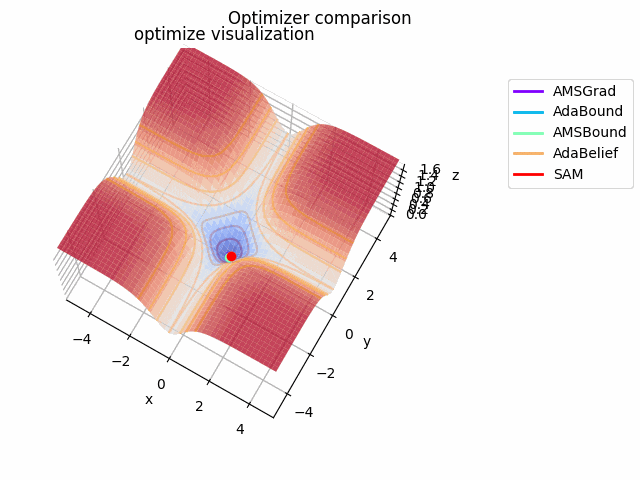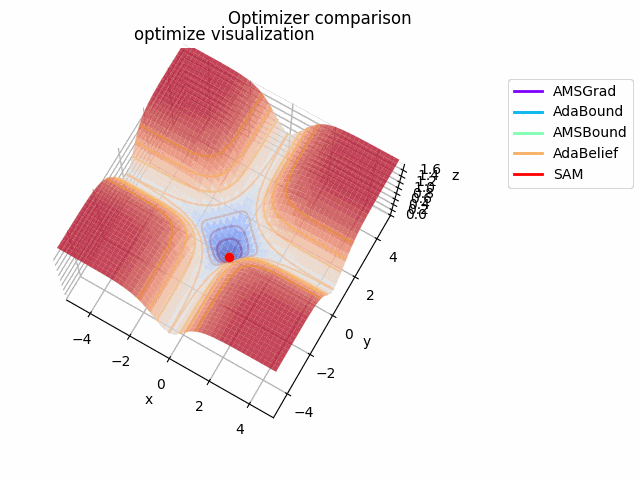
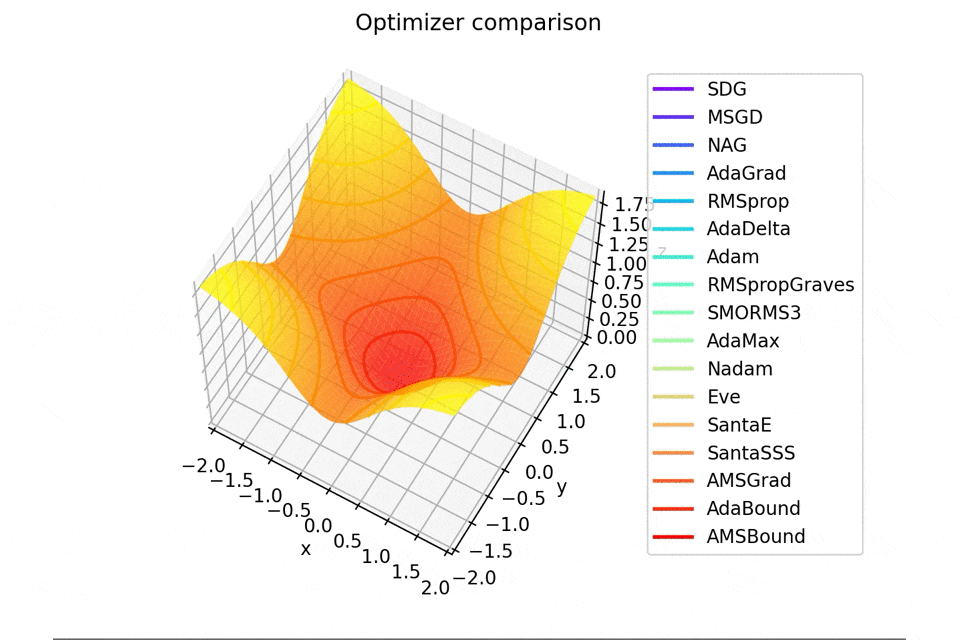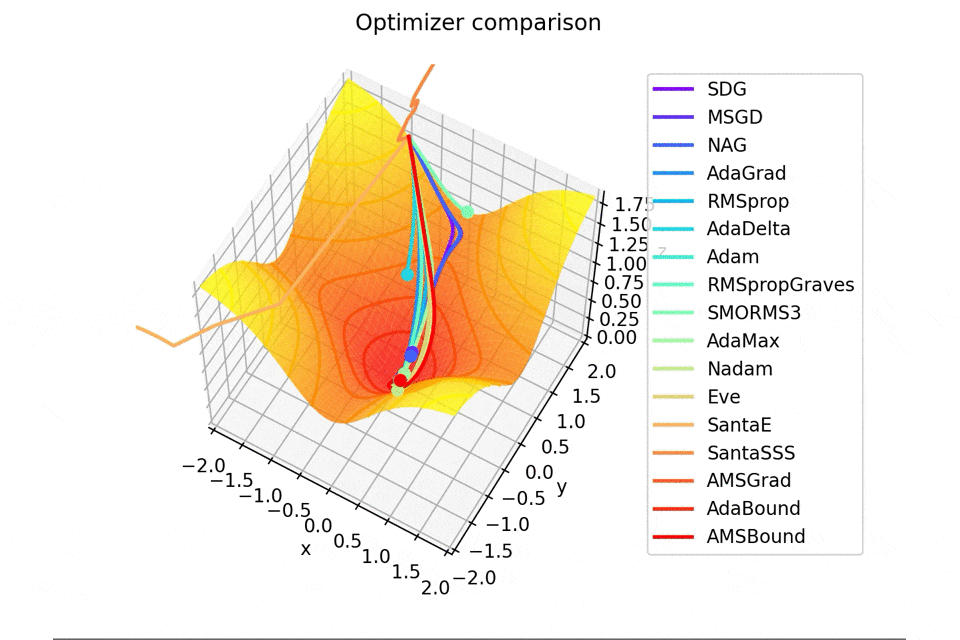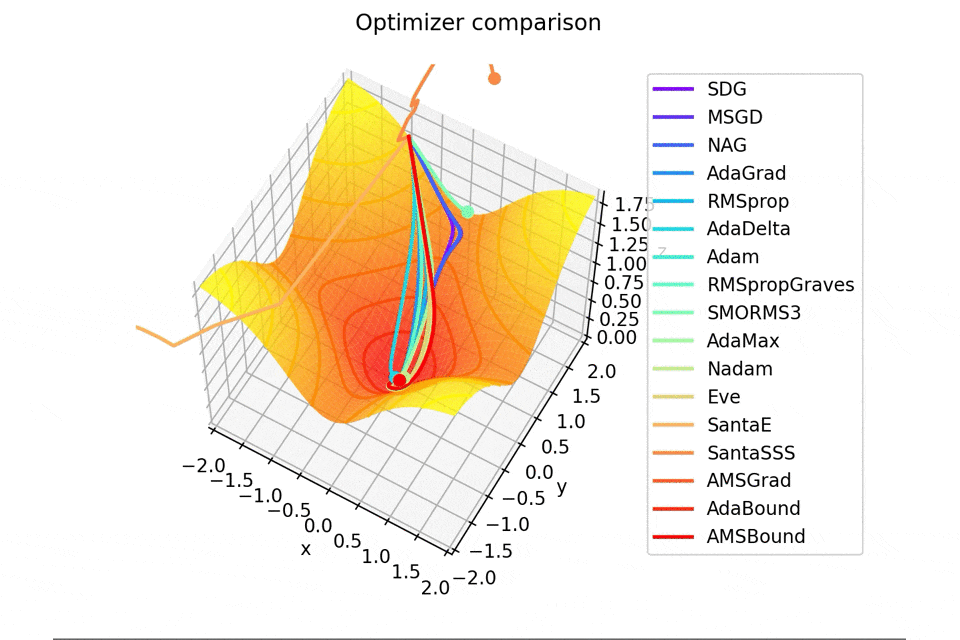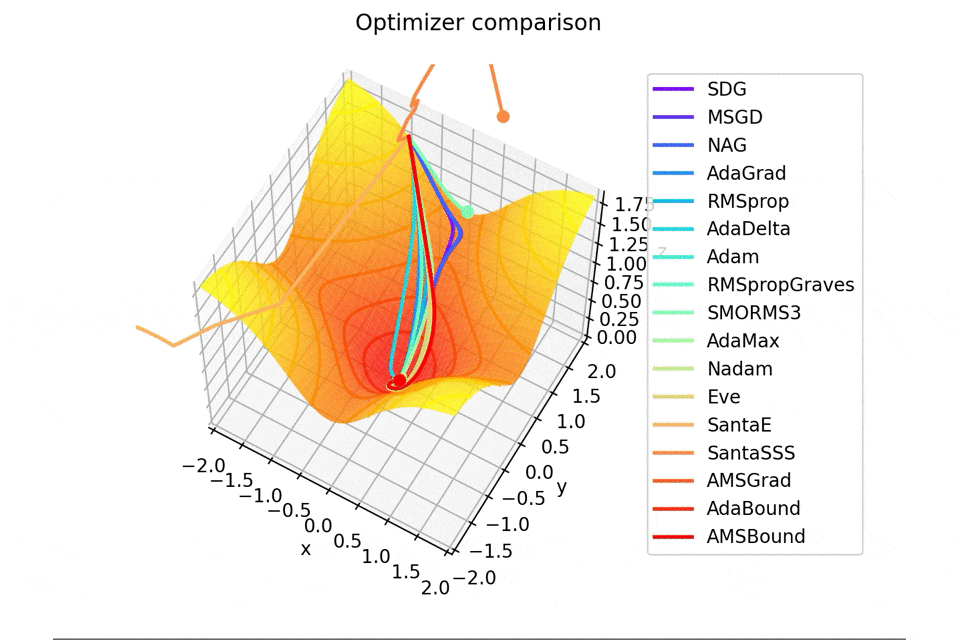
-sin(x)/x-sin(y)/y+(x^2+y^2)/7
続いて
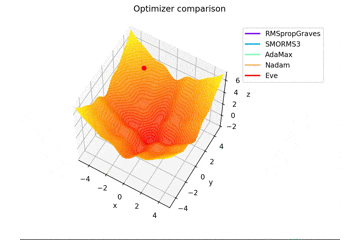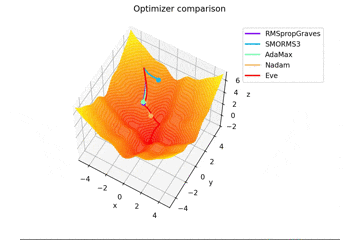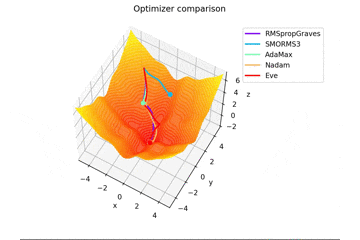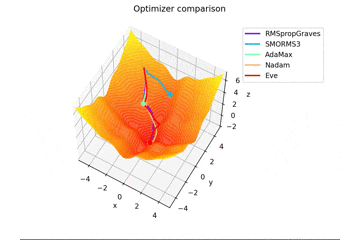
f(x, y) = -\cfrac{\sin (\pi x)}{\pi x} - \cfrac{\sin (\pi y)}{\pi y} + \cfrac{x^2+y^2}{7}
です。これだけ他と違い$x, y \in [-5, 5]$で、初期位置は$(x, y) = (-3, 4)$となっています。
絶妙に鞍点に嵌る学習則と嵌らない学習則とを作成するために$\frac{x^2+y^2}{7}$を足しています。
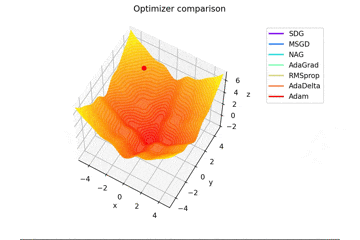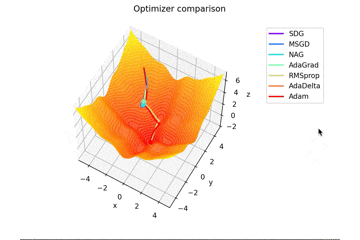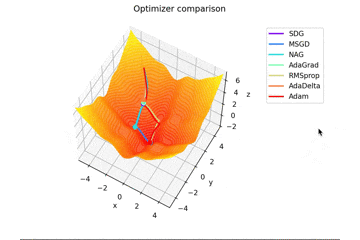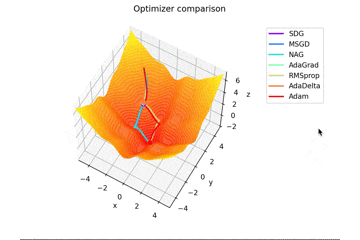
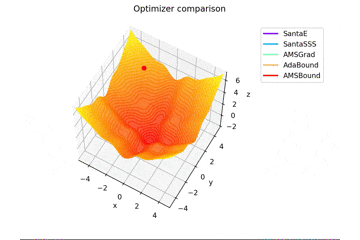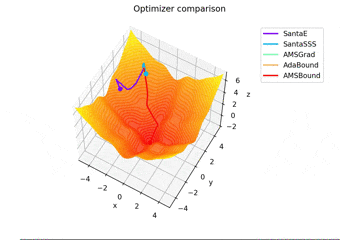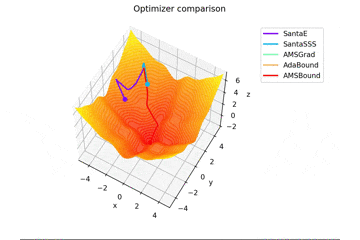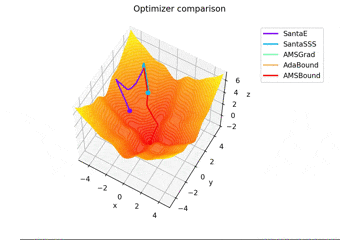
Santaの学習則における$N$についてですが、ぼくが論文を読む限りだとミニバッチの数かなと感じたので$N=1$としていますが、$N=16$とするとしっかり収束するんですよね...
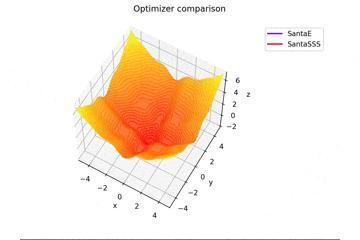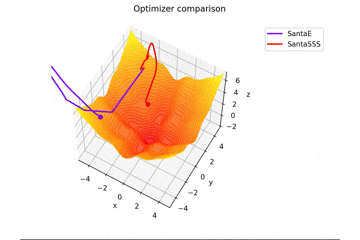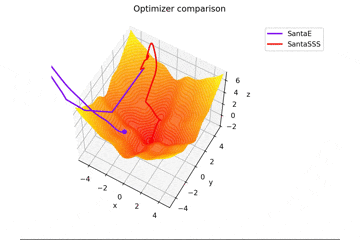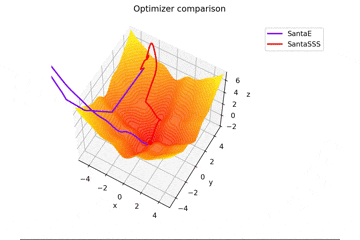
ちなみに$N=epoch$だと振動します。
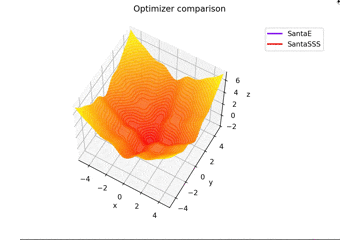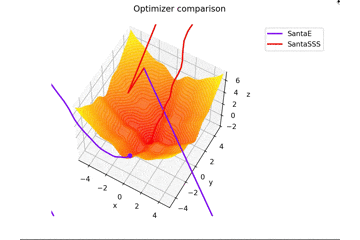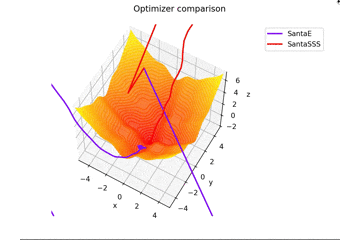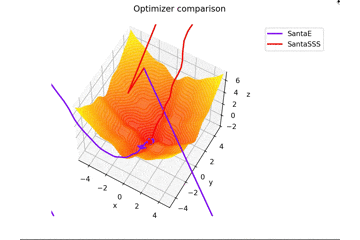
載せませんが、$epoch$を大きくして、$N=epoch$とすると塗り絵みたいになります笑
ということはやっぱりミニバッチの数という認識でいいんでしょう。実用上は$N=16,32$ですし、それくらいの値では微妙に振動するくらいなので。
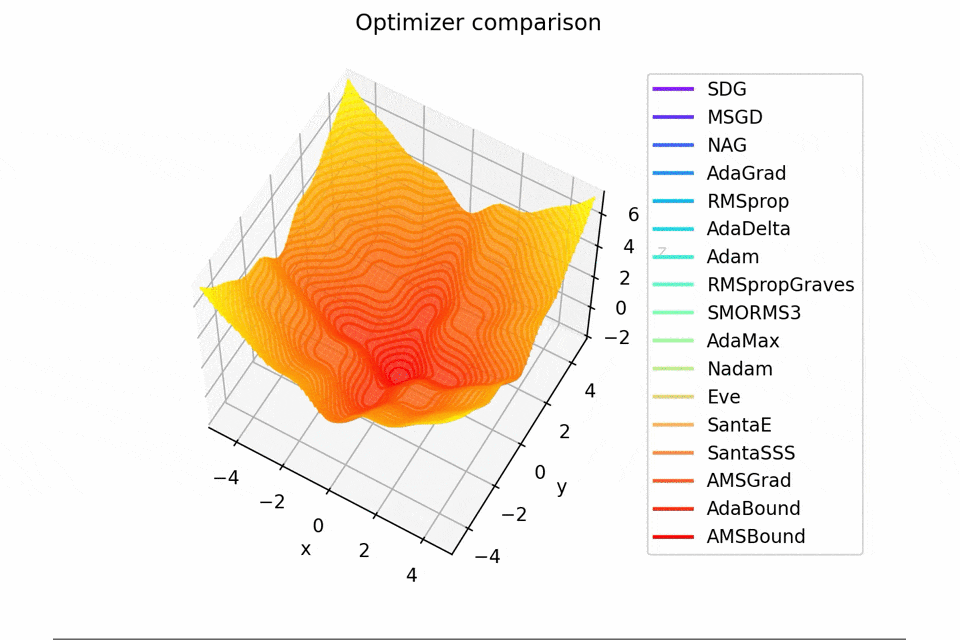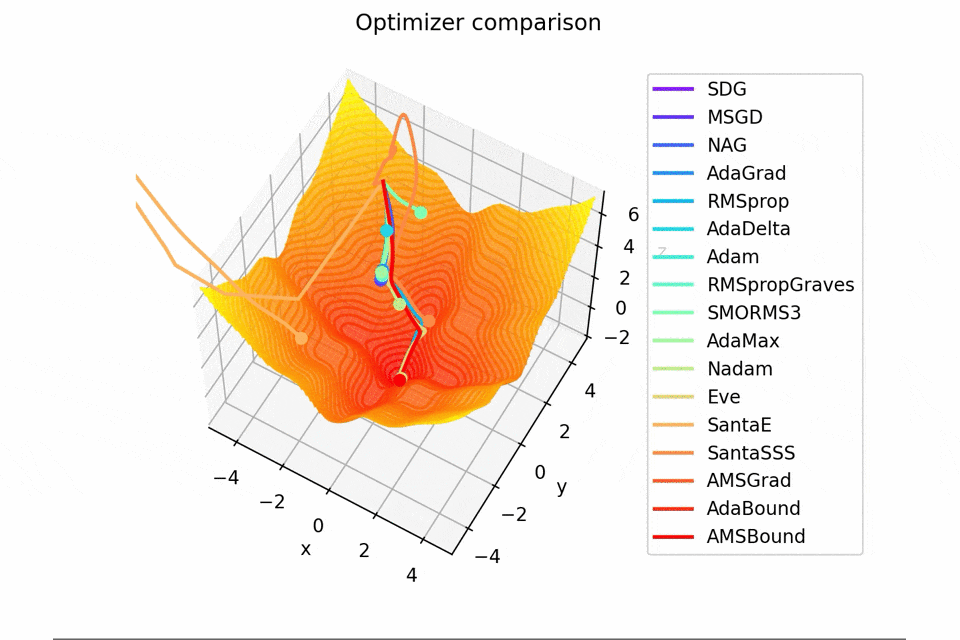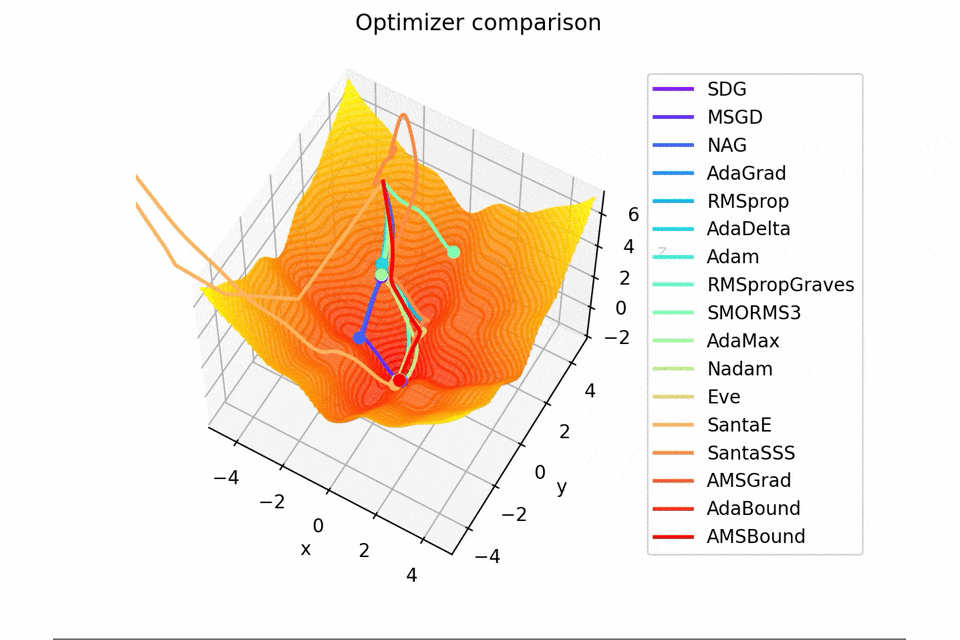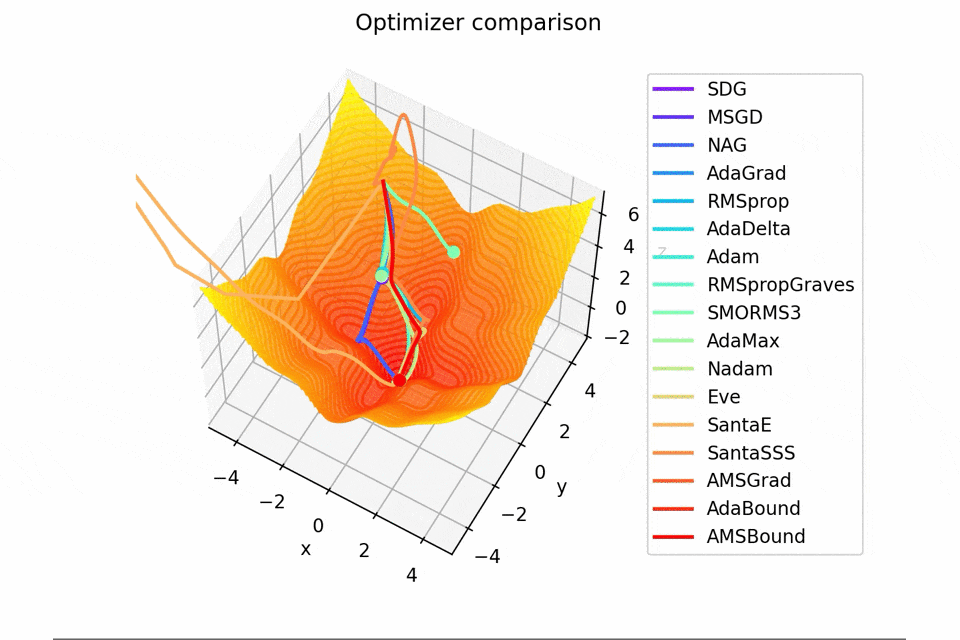
-sin(x)/x-sin(y)/y+(x^2+y^2)/10
2021/1/3に追加しました。
こちらも修正追加版です。
以前に載せていたものよりも2乗の係数を減らしてより明確な極小値を作り出し、ハマる最適化手法を多くしています。
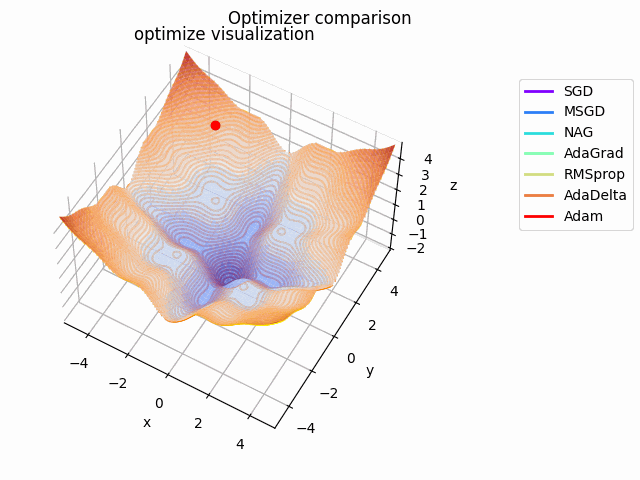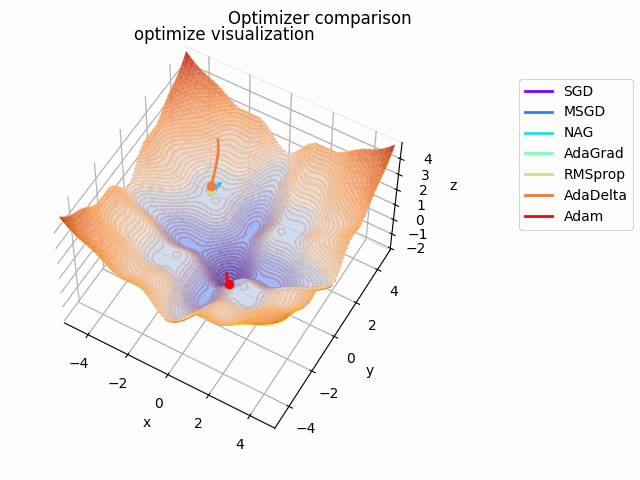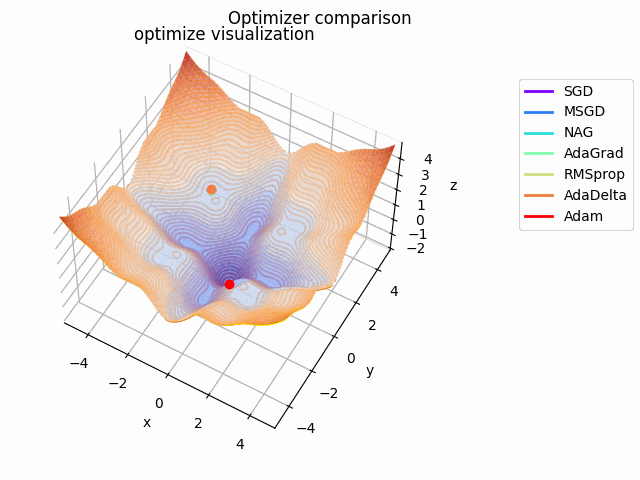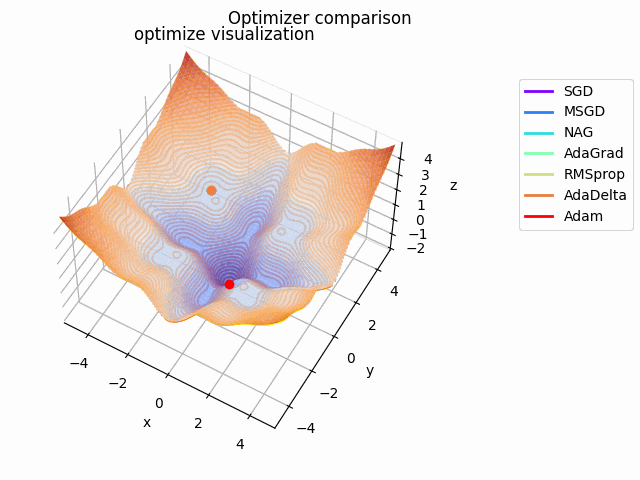
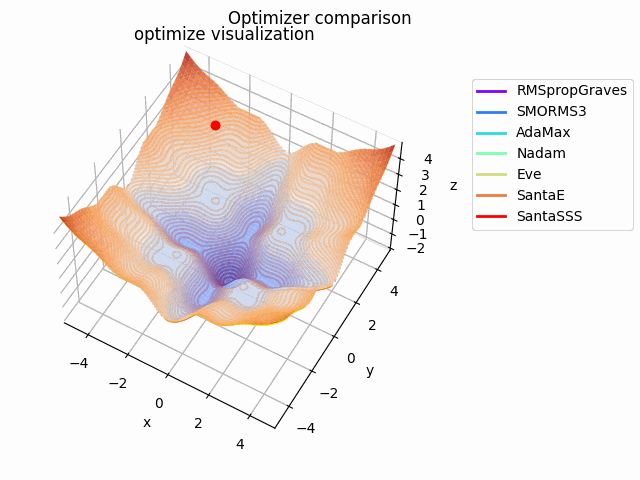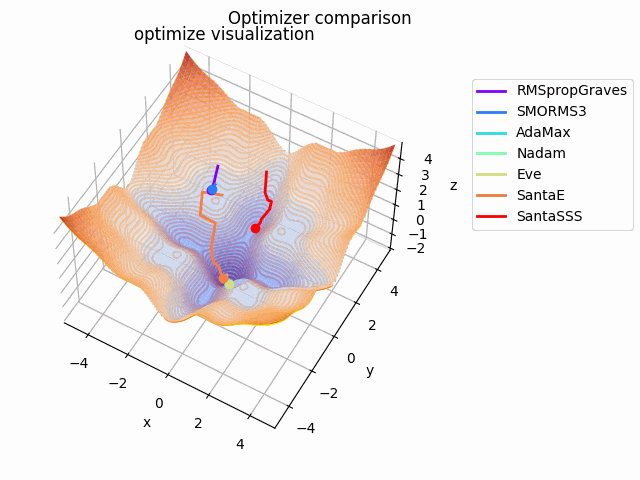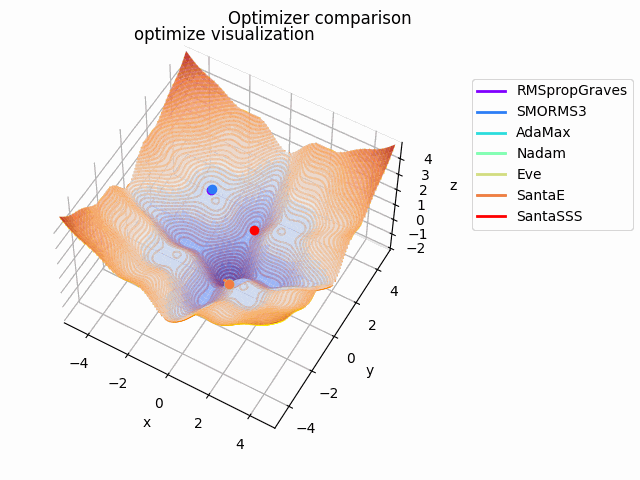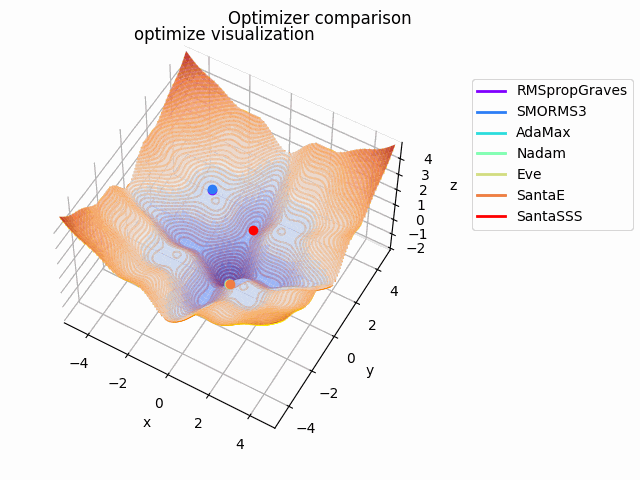
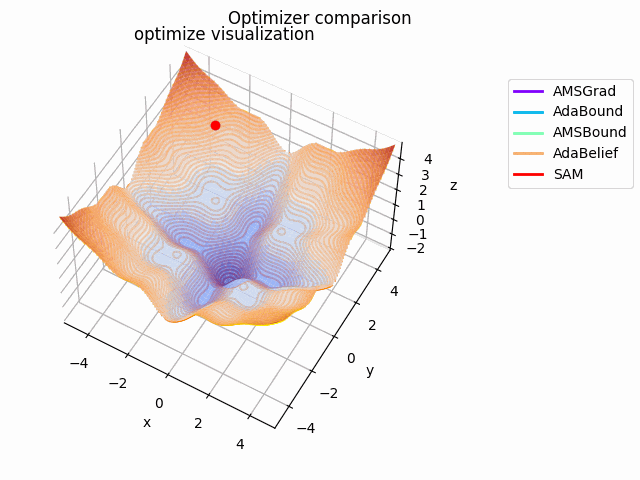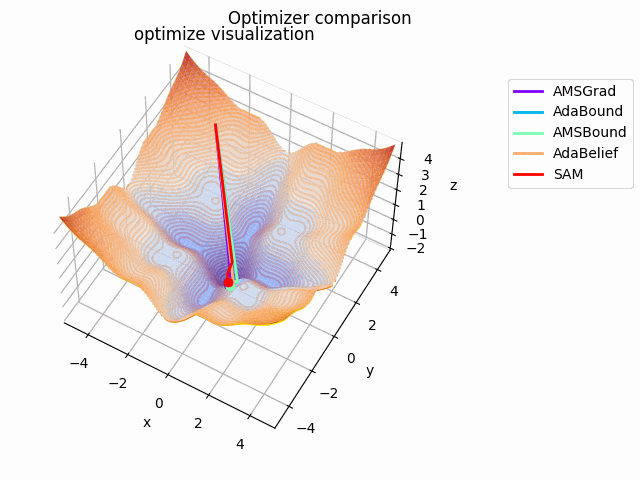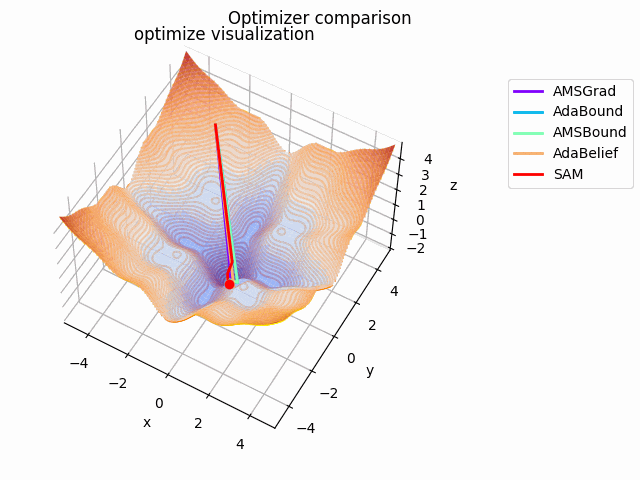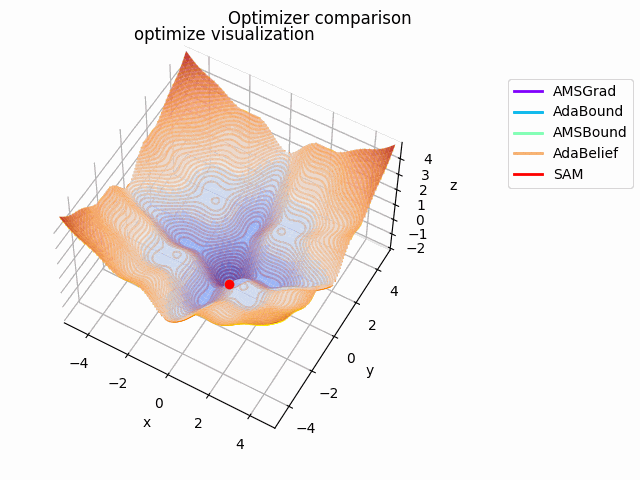
学習率大きすぎるかな...調整するかもしれません。
tanh(x)^2+(x^2+y^2)/8
2021/1/3に追加しました。
急峻な探索平面を作成してみました。もちろん学習率に依りますが、結構振動してる様子が見て取れて面白いですね。
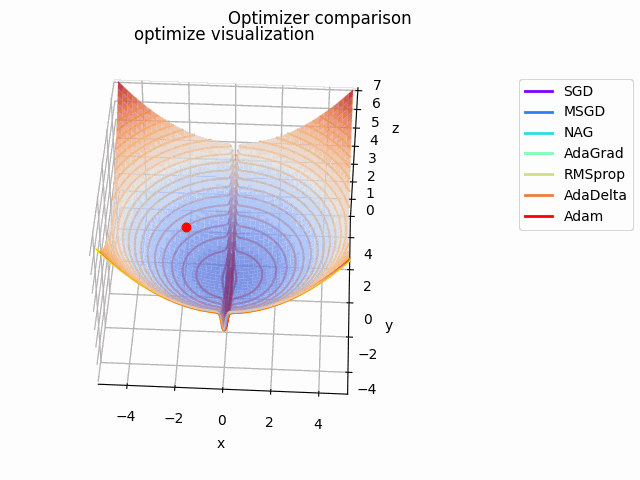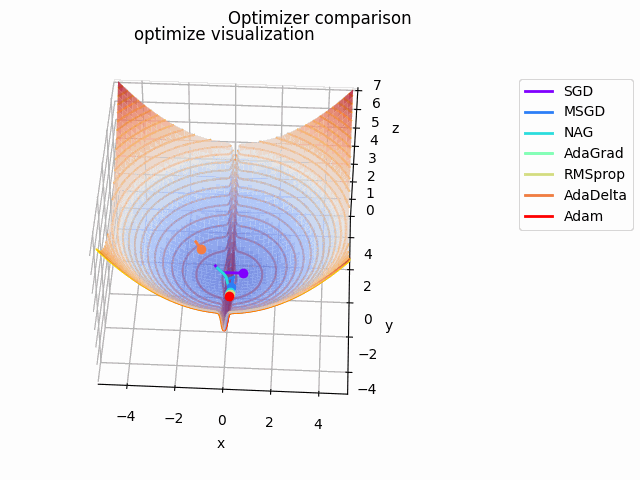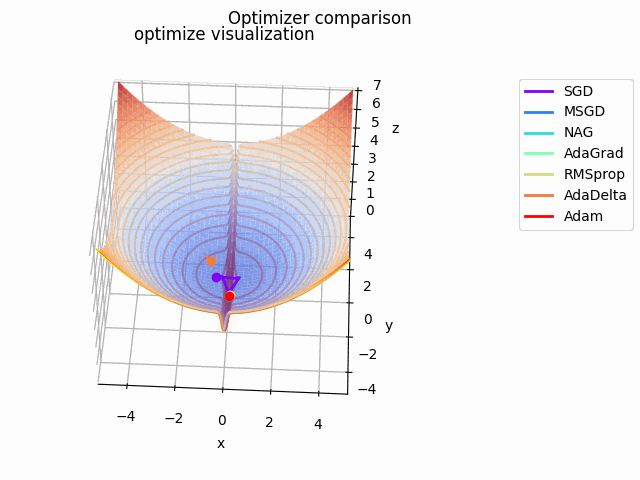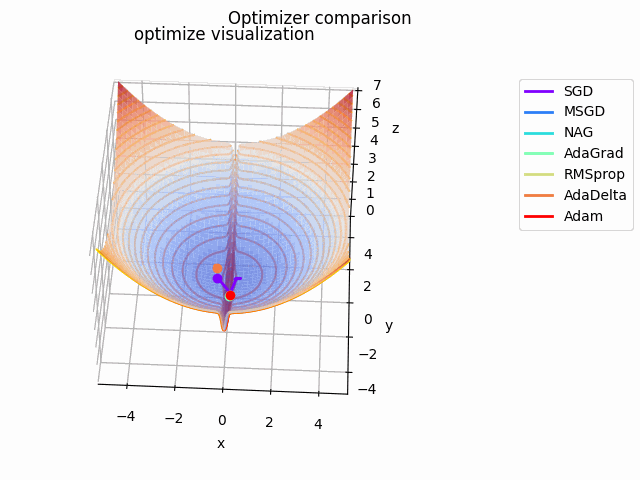
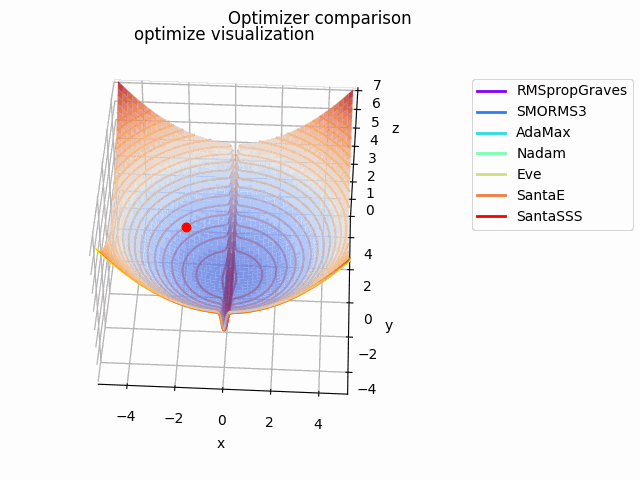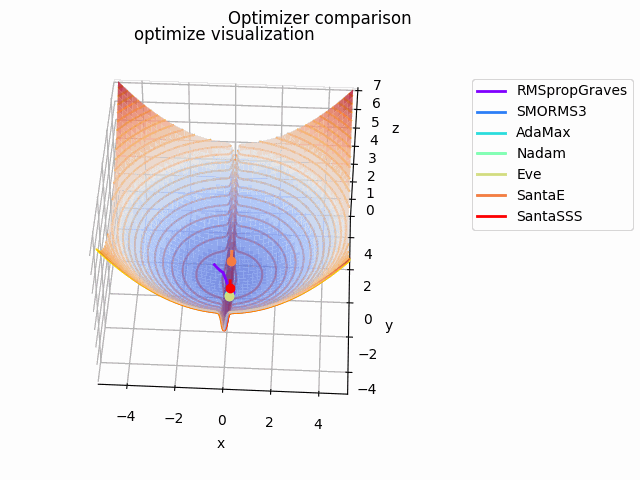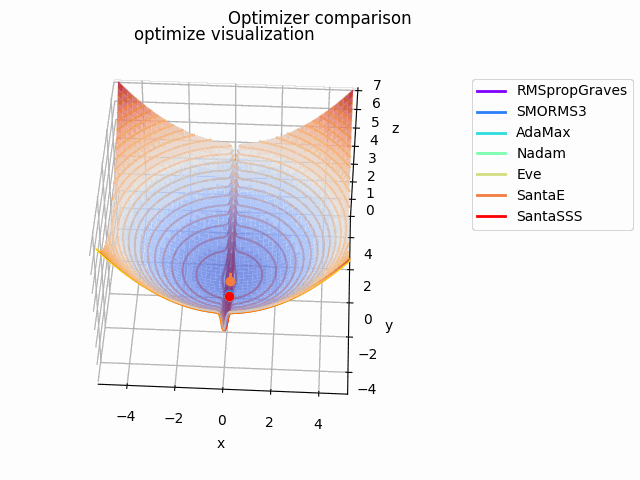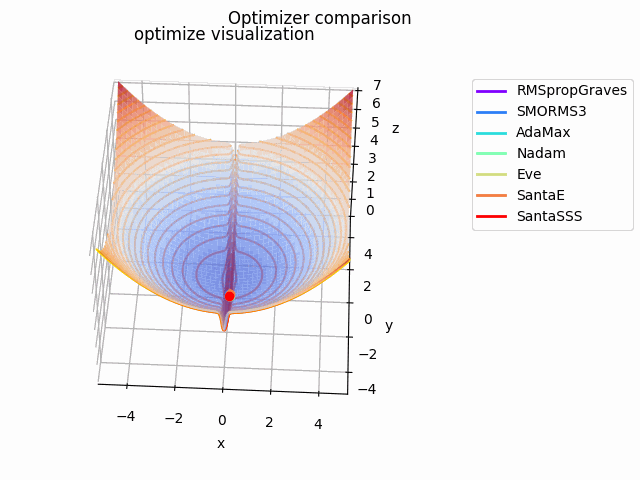
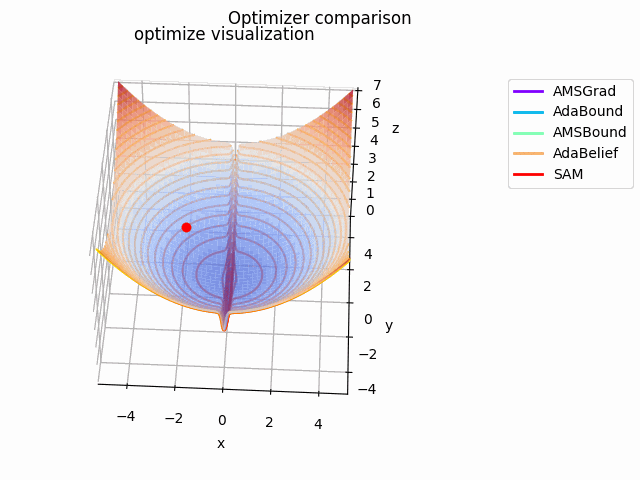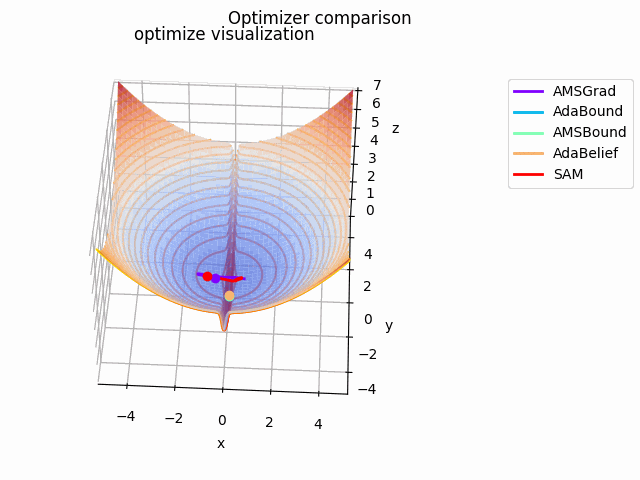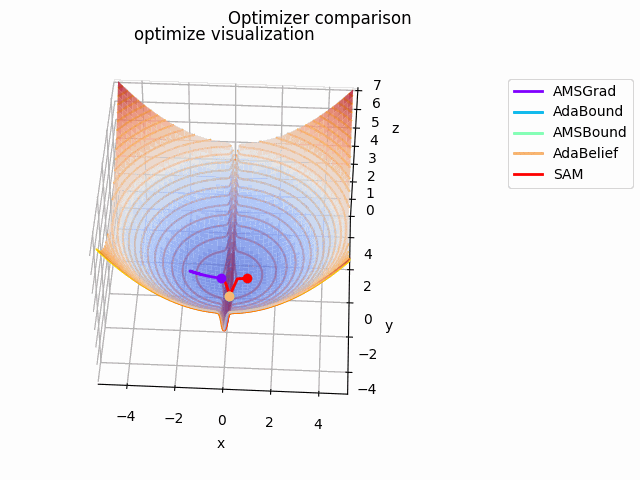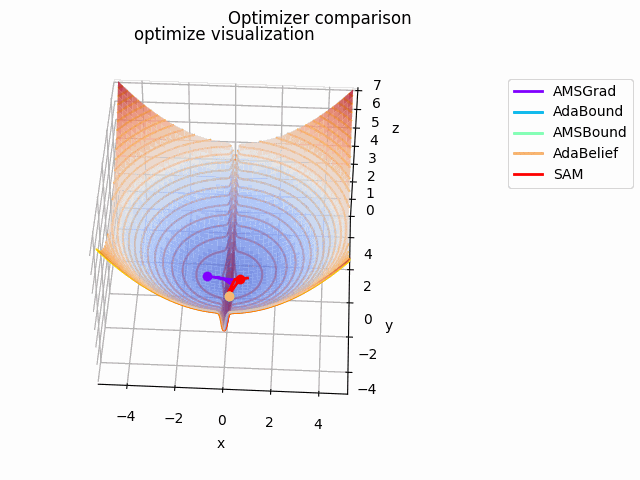
こちらの記事でAdaBeliefの優位性を説明されており、こちらの記事でSAMは平坦な極小値を探す、と述べてあるので、実際に比較してみました。
なお、見やすさのために使用する最適化手法はSGD、RMSprop、Adam、AdaBelief、SAMに絞っています。各最適化手法の学習率を以下のように調整しています。
- SGD、RMSpropは0.05
- Adam、AdaBeleifは0.005
- SAMの最適化手法はAdam(学習率0.25)
さらに、探索平面を少し変更して$\tanh^2x + \cfrac{0.5x^2 + 0.125y^2}{8}$とし、、$(x_0, y_0) = (-0.5, 0)$にして$x \in [-2, 2]$で計算、$x \in [-0.5, 0.5]$をクローズアップしてelevation=0.125、view_init=(25, -87)、frames=2^7で表示しています。
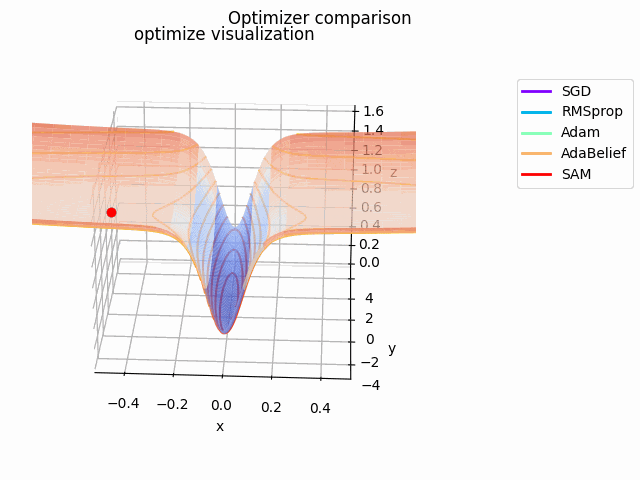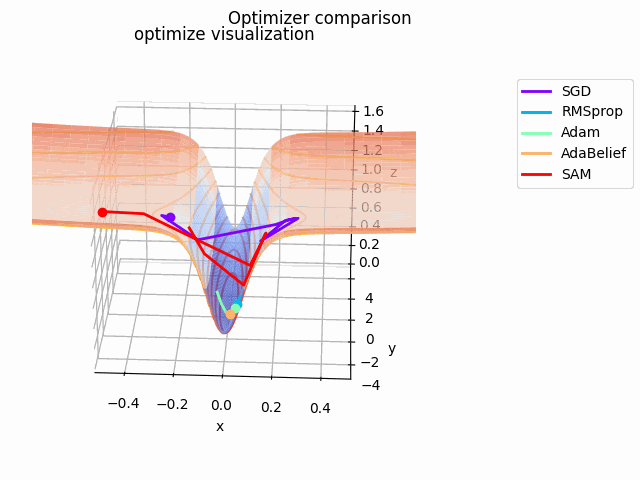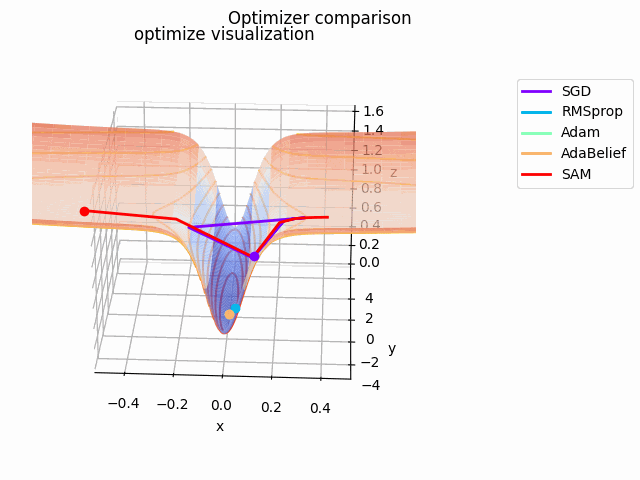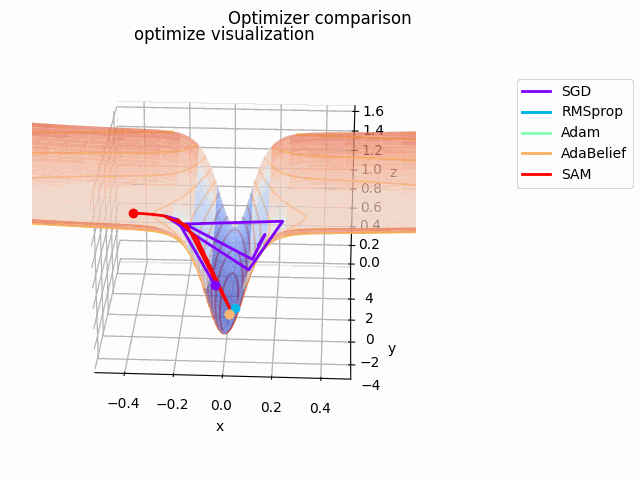
基本的にAdaBeliefが一番早く移動しています。次点でAdamが追随しています。SGDは平坦部分ではノロノロと動き、急峻な部分に差し掛かると飛び越えてしまっています。RMSpropには暴れてもらいました笑
SAMは何度も最適値付近に落ち込みつつも、平坦な面を探して飛び出しています。この動きによって過学習の可能性が高い急峻な最適値を回避しているんですね。
高画質版
使用したコード
こちらが実験コードとなります。
jupyter notebookでアニメーションを出力するとどうしても点や線が探索平面よりも下に表示されて見にくいため、ターミナル上で実行しています。
実験コード
from dataclasses import dataclass
import numpy as np
from numpy import ndarray
import matplotlib.pyplot as plt
import matplotlib.animation as anim
from mpl_toolkits.mplot3d import Axes3D
from _interface import get_opt
@dataclass
class _target():
test_type: int = 3
x: float = 0 # dummy for NAG.
grad: float = 0 # dummy for NAG.
def __post_init__(self, *args, **kwds):
if self.test_type == 1:
self.params = np.array([1e-4, 4.])
self.exact = np.array([5., 0.])
self.elevation = 1.
self.view_init = (35,)
self.epoch = 2**7
self.seed = 0
elif self.test_type == 2:
self.params = np.array([-1., 2.])
self.exact = np.array([0., 0.])
self.elevation = 0.25
self.view_init = (75,)
self.epoch = 2**7
self.seed = 0
elif self.test_type == 3:
self.params = np.array([-3., 4.])
self.exact = np.array([0., 0.])
self.elevation = 0.125
self.view_init = (55,)
self.epoch = 2**10
self.seed = 543
elif self.test_type == 4:
self.params = np.array([-2., 2.])
self.exact = np.array([0., 0.])
self.elevation = 0.25
self.view_init = (45, -87)
self.epoch = 2**8
self.seed = 3
# self.params = np.array([-0.5, 0.])
# self.elevation = 0.125
# self.view_init = (25, -87)
def forward(self, *args, **kwds):
if self.test_type == 1:
return self.params[1]**2 - self.params[0]**2
elif self.test_type == 2:
return np.tanh(self.params[0])**2 + np.tanh(self.params[1])**2
elif self.test_type == 3:
return (-(np.sinc(self.params[0])+np.sinc(self.params[1]))
+ (self.params[0]**2 + self.params[1]**2)/10)
elif self.test_type == 4:
return (0.125*(self.params[0]**2 + self.params[1]**2)
+ np.tanh(self.params[0]*10)**2)
# return (0.125*(0.5*self.params[0]**2 + 0.125*self.params[1]**2)
# + np.tanh(self.params[0]*10)**2)
def backward(self, *args, **kwds):
if self.test_type == 1:
dw = -2*self.params[0]
db = 2*self.params[1]
elif self.test_type == 2:
dw = 2 * np.tanh(self.params[0]) / np.cosh(self.params[0])**2
db = 2 * np.tanh(self.params[1]) / np.cosh(self.params[1])**2
elif self.test_type == 3:
dw = (np.sin(np.pi*self.params[0])/(np.pi * self.params[0]**2)
+ 2*self.params[0]/10
- np.cos(np.pi*self.params[0])/self.params[0])
db = (np.sin(np.pi*self.params[1])/(np.pi * self.params[1]**2)
+ 2*self.params[1]/10
- np.cos(np.pi*self.params[1])/self.params[1])
elif self.test_type == 4:
dw = (0.25*self.params[0]
+ 20 * np.tanh(self.params[0]*10)
/ np.cosh(self.params[0]*10)**2)
db = 0.25*self.params[1]
# dw = (0.5*0.25*self.params[0]
# + 20 * np.tanh(self.params[0]*10)
# / np.cosh(self.params[0]*10)**2)
# db = 0.125*0.25*self.params[1]
return np.array([dw, db])
def get_exact(self, *args, **kwds):
params = self.params.copy()
self.params = self.exact
exact_z = self.forward()
self.params = params
return exact_z
class TrajectoryAnimation3D(anim.FuncAnimation):
def __init__(self, paths, labels=[], fig=None, ax=None,
blit=True, coloring=None, **kwargs):
if fig is None:
if ax is None:
fig, ax = plt.subplots()
else:
fig = ax.get_figure()
else:
if ax is None:
ax = fig.gca()
self.fig = fig
self.ax = ax
self.paths = paths
frames = paths.shape[0]
self.lines = []
self.points = []
for j, opt in enumerate(labels):
line, = ax.plot([], [], [], label=opt, lw=2, color=coloring[j])
point, = ax.plot([], [], [], marker="o", color=coloring[j])
self.lines.append(line)
self.points.append(point)
super().__init__(fig, self.animate,
frames=frames, blit=blit, **kwargs)
def animate(self, i):
start = 0 if i-8 < 0 else i-8
j = 0
for line, point in zip(self.lines, self.points):
line.set_data(self.paths[start:i+1, j, 0],
self.paths[start:i+1, j, 1])
line.set_3d_properties(self.paths[start:i+1, j, 2])
line.set_zorder(i+100)
point.set_data(self.paths[i, j, 0], self.paths[i, j, 1])
point.set_3d_properties(self.paths[i, j, 2])
point.set_zorder(i+101)
j += 1
return self.lines + self.points
def opt_plot():
objective = _target(test_type=4)
start_x, start_y = objective.params
start_z = objective.forward()
x_range = np.arange(-5, 5, 1e-2)
# x_range = np.arange(-2, 2, 1e-2)
y_range = np.arange(-5, 5, 1e-2)
X, Y = np.meshgrid(x_range, y_range)
objective.params = np.array([X, Y])
Z = objective.forward()
elevation = np.arange(np.min(Z), np.max(Z), objective.elevation)
exact_z = objective.get_exact()
epoch = objective.epoch
frames = 2**6
# frames = 2**7
fps = 10
np.random.seed(seed=objective.seed)
opt_dict = {
"SGD": get_opt("sgd", eta=0.0875),
"MSGD": get_opt("msgd", eta=0.1),
"NAG": get_opt("nag", parent=objective, eta=0.1),
"AdaGrad": get_opt("adagrad", eta=0.25),
"RMSprop": get_opt("rmsprop", eta=0.05),
"AdaDelta": get_opt("adadelta", rho=0.9999),
"Adam": get_opt("adam", alpha=0.25),
"RMSpropGraves": get_opt("rmspropgraves", eta=0.0125),
"SMORMS3": get_opt("smorms3", eta=0.05),
"AdaMax": get_opt("adamax", alpha=0.5),
"Nadam": get_opt("nadam", alpha=0.5),
"Eve": get_opt("eve", f_star=exact_z, alpha=0.25),
"SantaE": get_opt("santae", burnin=epoch/2**3, N=1,
eta=0.0125),
"SantaSSS": get_opt("santasss", burnin=epoch/2**3, N=1,
eta=0.0125),
"AMSGrad": get_opt("amsgrad", alpha=0.125),
"AdaBound": get_opt("adabound", alpha=0.125),
"AMSBound": get_opt("amsbound", alpha=0.125),
"AdaBelief": get_opt("adabelief", alpha=0.25),
"SAM": get_opt("sam", parent=objective,
opt_dict={"alpha": 0.25})
}
# opt_dict["SGD"] = get_opt("sgd", eta=0.05)
# opt_dict["RMSprop"] = get_opt("rmsprop", eta=0.05)
# opt_dict["Adam"] = get_opt("adam", alpha=0.005)
# opt_dict["AdaBelief"] = get_opt("adabelief", alpha=0.005)
# opt_dict["SAM"] = get_opt("sam", parent=objective,
# opt_dict={"alpha": 0.25})
key_len = len(max(opt_dict.keys(), key=len))
current_x = np.full(len(opt_dict), start_x)
current_y = np.full(len(opt_dict), start_y)
current_z = np.full(len(opt_dict), start_z)
paths = np.zeros((frames, len(opt_dict), 3))
cmap = plt.get_cmap("rainbow")
coloring = [cmap(i) for i in np.linspace(0, 1, len(opt_dict))]
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
fig.suptitle("Optimizer comparison")
ax.set_title("optimize visualization")
ax.set_position([0., 0.1, 0.7, 0.8])
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.grid()
ax.set_xlim([x_range[0], y_range[-1]])
# ax.set_xlim([-0.5, 0.5])
ax.set_ylim([y_range[0], y_range[-1]])
ax.set_zlim([elevation[0], elevation[-1]])
ax.view_init(*objective.view_init)
ax.plot_surface(X, Y, Z, cmap="coolwarm", zorder=-10, alpha=0.75)
ax.contour(X, Y, Z, cmap="autumn", levels=elevation, zorder=-5, alpha=0.75)
for i in range(1, epoch+1):
for j, opt in enumerate(opt_dict):
if (i-1) % (epoch//frames) == 0:
paths[(i-1)//(epoch//frames), j, 0] = current_x[j]
paths[(i-1)//(epoch//frames), j, 1] = current_y[j]
paths[(i-1)//(epoch//frames), j, 2] = current_z[j]
objective.params = np.array([current_x[j], current_y[j]])
dx, dy = opt_dict[opt].update(objective.backward(),
t=i, f=objective.forward())
objective.params += np.array([dx, dy])
current_x[j] += dx
current_y[j] += dy
current_z[j] = objective.forward()
ani = TrajectoryAnimation3D(paths, labels=opt_dict, fig=fig, ax=ax,
coloring=coloring)
fig.legend(bbox_to_anchor=(1., 0.85))
ani.save("optimizers_3d.gif", writer="pillow", fps=fps)
if __name__ == "__main__":
opt_plot()
参考
- matplotlibで3Dプロット
- matplotlibのアニメーション機能で立体(3D)地形図を回転してみる
- Visualizing and Animating Optimization Algorithms with Matplotlib
#深層学習シリーズ