オミータです。ツイッターで人工知能のことや他媒体の記事など を紹介していますので、人工知能のことをもっと知りたい方などは @omiita_atiimoをご覧ください!
他にも次のような記事を書いていますので興味があればぜひ!
SoTAを総なめ!衝撃のオプティマイザー「SAM」爆誕&解説!
ICLR2021に衝撃的な手法が登場しました。その名もSharpness-Aware Minimization、通称SAMです。どれくらい衝撃かというと、画像分類タスクにおいて、SAMがImageNet(88.61%)/CIFAR-10(99.70%)/CIFAR-100(96.08%)などを含む9つものデータセットでSoTAを更新したくらいです(カッコ内はSAMによる精度)。話題のVision Transformer(ViT)のImageNetの結果(88.55%)を早速超しました(SoTA更新早すぎます)。SAMもViTと同様まだICLR2021レビュー中ではありますが、レビュワーの評価を見る限りICLR2021にアクセプトされるでしょう。そんな衝撃的な手法SAMについてじっくりと見ていきます!少し数式が登場しますが、丁寧に手順を追って説明しているのでぜひ理解しながら読んでみてください。
本記事の流れ:
- 忙しい方へ
- SAMの説明
- SAMの実験
- まとめと所感
- 参考
原論文: "Sharpness-Aware Minimization for Efficiently Improving Generalization", Foret, P., Kleiner, A., Mobahi, H., Neyshabur, B. (2020)
公式実装: JAX/Flax
非公式実装: PyTorch
| 略語 | 正式名称 |
|---|---|
| SAM(提案手法) | Sharpness-aware Minimization |
| DA | Data Augmentation |
| SGD | Stochastic Gradient Descent |
0. 忙しい方へ
- SAMは損失が最小かつその周辺が平坦であるようなパラメータを目指すよ
-
SAMは次の3ステップだよ
- パラメータ$\mathbf{w}$の周辺で最大の損失をとる$\mathbf{w+\hat{\epsilon}(w)}$を求めるよ
- $\mathbf{w+\hat{\epsilon}(w)}$における損失を求めるよ
- 2.の損失に対する勾配でパラメータ$\mathbf{w}$を更新するよ
- SAMは一言で言ってしまえば、「パラメータ周辺での最大の損失を求めて、それが下がる方向でパラメータを更新する」ものだよ
- ImageNetやCIFARを含む9つの画像分類データセットでSoTAを更新したよ
- ラベルへのロバスト性も高いよ
1. SAMの説明
SAMは至ってシンプルです。というのも、今までは損失が最小になるパラメータを学習させていました。ただ、SAMは損失が最小かつその周りも平坦となっているパラメータを探しに行きます。つまり、下図のような損失平面においては今までは左図のようなただひたすら最小値となるパラメータを探していたのですが、SAMは右図のような最小かつ(比較的)平坦なパラメータを探していきます。平坦さが汎化性能と関係していることは過去の研究でわかっています。
上図は、SGD(左)またはSAM(右)で学習させたResNetの損失平面を可視化したものです。この最小かつ平面であるパラメータを探させるために、SAMでは最小化問題の損失関数に少し変更を加えています。
1.1 SAMの式
SAMでは以下のような式を最小化させていきます。
\min_{\mathbf{w}} L_\mathcal{S}^\text{SAM}(\mathbf{w})+\lambda\|\mathbf{w}\|_2^2 \tag{1}
ここで、$\mathcal{S}$はデータの集合、$\mathbf{w}$はニューラルネットのパラメータ、$\lambda$は係数でハイパーパラメータです。第1項 $L_{\mathcal{S}}^\text{SAM}(\mathbf{w})$ がまさに最小かつ平面を求めさせているものです。第2項 $\lambda || \mathbf{w} ||_{2}^{2}$ はただのL2正則化です。それではこの第1項について少し詳しく見ていきます。$L_\mathcal{S}^\text{SAM}$は以下で定義されています。
L_\mathcal{S}^\text{SAM}(\mathbf{w}) \triangleq \max_{\|\mathbf{\epsilon}\|_p\leq\rho} L_\mathcal{S}(\mathbf{w}+\mathbf{\epsilon})
ここで、$L_\mathcal{S}$は通常の損失関数のことでクロスエントロピーや二乗誤差などが入ってきます。$p$はノルムを決定するもので論文中では$p=2$(i.e. L2ノルム)が使われます。$\rho$はneighborhood(=近傍)サイズと呼ばれるハイパーパラメータです。この$\rho$については上式の意味を説明した後の方が理解しやすいと思います。上式を言葉で表すと、$L_\mathcal{S}^\text{SAM}$とはパラメータ$w$の周辺$\rho$たちのなかで一番大きい損失ということになります。$\mathbf{w+\epsilon}$がその時のパラメータの値ということですね。$||\mathbf{\epsilon}||_p\leq\rho$という条件からも損失が最大となるような$\mathbf{\epsilon}$は$\rho$の範囲内で探すので$\rho$がneighborhood(=近傍)パラメータと呼ばれるのですね。$L_\mathcal{S}^\text{SAM}(\mathbf{w})$を最小化するということは1点だけでなくその周辺$\rho$内も等しく損失が小さいようなパラメータ$w$を求めるということになります。
SAMの仕組みはこれだけになるのですが、式(1)を少しだけ式変形するとまた別の角度で式の意味が理解ができるかもしれません。式(1)に通常の損失を表す$L_\mathcal{S}(\mathbf{w})$の項を無理やりねじ込んでみると下式になります。
\min_\mathbf{w} [\max_{\|\mathbf{\epsilon}\|_p\leq\rho} L_\mathcal{S}(\mathbf{w}+\mathbf{\epsilon}) - L_\mathcal{S}(\mathbf{w})] + L_\mathcal{S}(\mathbf{w}) + \lambda\|\mathbf{w}\|_2^2
第2項$L_\mathcal{S}(\mathbf{w})$は通常の損失で第3項$\lambda||\mathbf{w}||_2^2$はL2正則化です。第1項$[\max_{||\mathbf{\epsilon}||_p\leq\rho} L_\mathcal{S}(\mathbf{w}+\mathbf{\epsilon}) - L_\mathcal{S}(\mathbf{w})]$はsharpness項とも名付けられており周辺で一番大きい損失とどれだけの差があるか(i.e. 鋭さ)を表しています。上の分解からも、式(1)を最小化することで損失の最小かつ平面の2つを達成できることがわかりますね。あとは$L_\mathcal{S}^\text{SAM}(\mathbf{w})$の勾配を求めれれば終わりです。ただそのためには1つ求めないといけないものがいます。それは、近傍$\rho$で損失が最大となるような$\epsilon$ です。
1.2 epsilonの定義
近傍$\rho$内で損失が最大となるような$\epsilon$は次式のように定義できます。見たままです。
\mathbf{\epsilon}^*(\mathbf{w})\triangleq \text{argmax} _{\|\epsilon\|_p\leq\rho} L_\mathcal{S}(\mathbf{w+\epsilon})
続いてこれを$\epsilon$における1次マクローリン展開(つまり多項式で近似)をすると、
\mathbf{\epsilon}^*(\mathbf{w}) \triangleq \text{argmax}_{\|\epsilon\|_p\leq\rho} L_\mathcal{S}(\mathbf{w+\epsilon}) \approx \text{argmax}_{\|\epsilon\|_p\leq\rho} L_\mathcal{S}(\mathbf{w}) + \epsilon^T\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})
となり、右辺第1項は$\epsilon$がいないので、
\mathbf{\epsilon}^*(\mathbf{w}) \approx \text{argmax}_{\|\epsilon\|_p\leq\rho} \epsilon^T\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})
となります。これを満たす$\epsilon$はdual norm problemで与えられ次式で表されるようです。(このdual norm problemは分かる方がいればコメントかDMでご教示いただきたいです。。。)
\mathbf{\hat{\epsilon}(w)} = \rho\space\text{sign}(\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})) \frac{ |\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})|^{q-1} }{ (\|\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})\|^q_q)^{1/p} } \tag{2}
ここで$1/p+1/q=1$となります。特に、本論文ではL2ノルムつまり$p=2$を取り扱っているので$q=2$となります。これらを上式に代入すると、
\mathbf{\hat{\epsilon}(w)} = \rho\space\text{sign}(\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})) \frac{ |\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})| }{ \|\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})\|_2 } = \rho\space \frac{ \nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w}) }{ \|\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})\|_2 }
となり$p=2$においては、周辺で最大の損失を取る $\epsilon$とは、勾配$\nabla_\mathbf{w}L_\mathcal{S}(\mathbf{w})$のノルムをneighborhood size$\rho$でリスケールしたものであることがわかります。
1.3 SAMの勾配
それでは式(2)で$\mathbf{\hat{\epsilon}(w)}$が求まったので遂に$\nabla_\mathbf{w} L_\mathcal{S}^\text{SAM}(\mathbf{w})$を求めてみましょう。まず$L_\mathcal{S}^\text{SAM}(\mathbf{w})$の定義式と式(2)から、
L_\mathcal{S}^\text{SAM}(\mathbf{w}) \triangleq \max_{\|\mathbf{\epsilon}\|_p\leq\rho} L_\mathcal{S}(\mathbf{w}+\mathbf{\epsilon}) \approx L_\mathcal{S}(\mathbf{w}+\mathbf{\hat{\epsilon}}(\mathbf{w}))
あとは勾配を求めます。$\mathbf{w}$による合成関数の微分なので、
\nabla_\mathbf{w} L_\mathcal{S}^\text{SAM}(\mathbf{w}) \approx \nabla_\mathbf{w} L_\mathcal{S}(\mathbf{w}+\mathbf{\hat{\epsilon}}(\mathbf{w})) = \frac{d(\mathbf{w}+\mathbf{\hat{\epsilon}}(\mathbf{w}))}{d\mathbf{w}} \nabla_\mathbf{w} L_\mathcal{S}(\mathbf{w})|_{\mathbf{w}+\mathbf{\hat{\epsilon}}(\mathbf{w})} \\
= \nabla_\mathbf{w} L_\mathcal{S}(\mathbf{w})|_{\mathbf{w}+\mathbf{\hat{\epsilon}}(\mathbf{w})} +\frac{d\mathbf{\hat{\epsilon}}(\mathbf{w})}{d\mathbf{w}} \nabla_\mathbf{w} L_\mathcal{S}(\mathbf{w})|_{\mathbf{w}+\mathbf{\hat{\epsilon}}(\mathbf{w})}
となります。ここで$\mathbf{\hat{\epsilon}}(\mathbf{w})$は$\nabla_\mathbf{w} L_\mathcal{S}(\mathbf{w})$を含んでいるため第2項は二階微分となっています。そのため、本論文では効率性を上げるために第2項は無視しています。結果として、SAMの勾配は次のようになります。
\nabla_\mathbf{w} L_\mathcal{S}^\text{SAM}(\mathbf{w}) \approx \nabla_\mathbf{w} L_\mathcal{S}(\mathbf{w})|_{\mathbf{w}+\mathbf{\hat{\epsilon}}(\mathbf{w})}
これを言葉で表すと、SAMの勾配は、結局$\mathbf{w+\hat{\epsilon}(w)}$における損失を$\mathbf{w}$で微分してあげれば良いだけです。そのため、実際に実装するアルゴルズムは次のような3ステップになりそうなことがわかります。
- 近傍$\rho$で損失が最大となるような $\mathbf{\hat{\epsilon}(w)}$を算出
- $\mathbf{w+\hat{\epsilon}(w)}$における損失
- 2.の損失の勾配でパラメータ$\mathbf{w}$を更新
次節で実際の疑似コードを見てみましょう。
1.4 SAMの疑似コード
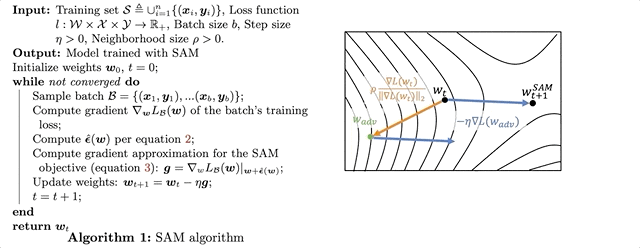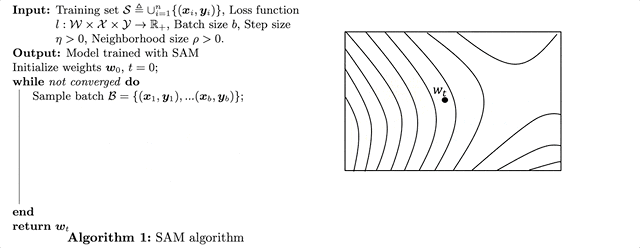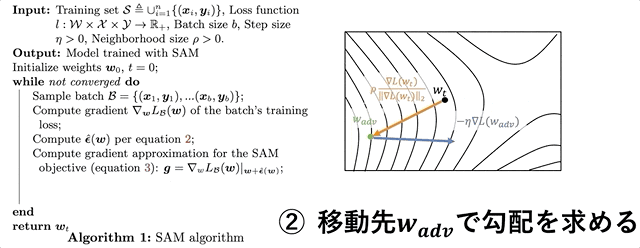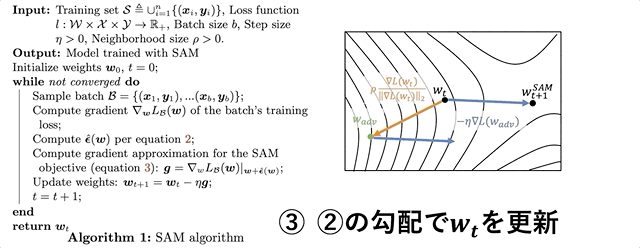
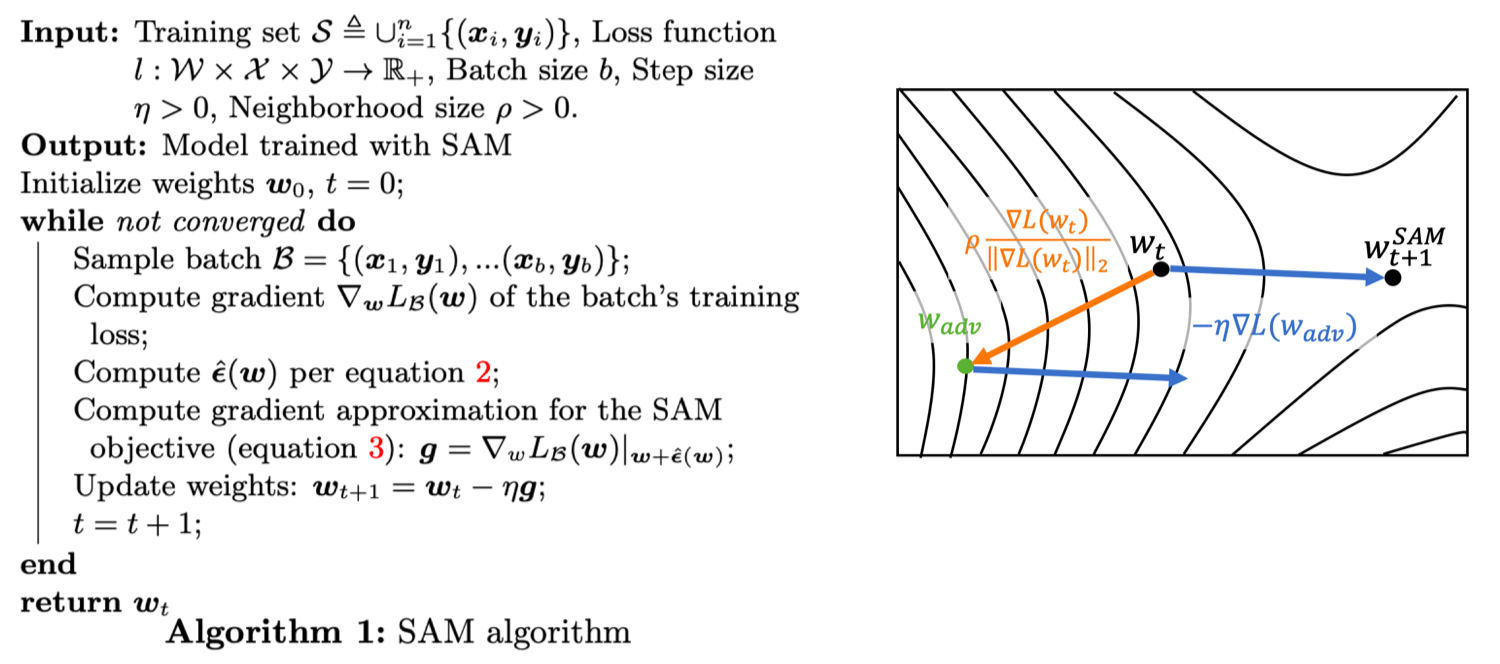
左が疑似コード、右がその模式図になります。上図は論文中の図をわかりやすいように少しだけ加工しています。前述しましたが、ここで行われているのは次のような3ステップです。
- 近傍$\rho$で損失が最大となるような $\mathbf{\hat{\epsilon}(w)}$を算出
- $\mathbf{w+\hat{\epsilon}(w)}$における損失
- 2.の損失の勾配でパラメータ$\mathbf{w}$を更新
ちなみにステップ3はSGDによる更新式になっていますが、ここはAdamやら自分の使いたいオプティマイザーなんでも大丈夫です。この3つの手順を下のようにアニメーションにしてみました。
SAMのアルゴリズムに関してはこれにて説明は終わりですが、勘の鋭い方はSAMの弱点に気づいているかもしれません。それは、1回の更新に2回も勾配を求めていることです。具体的には、$\mathbf{\hat{\epsilon}(w)}$を求めるとき($\nabla_\mathbf{w} L(\mathbf{w}_t)$,ステップ1)と$w_\text{adv}$での勾配を求めるとき($\nabla_\mathbf{w} L(\mathbf{w}_\text{adv})$,ステップ2)です。そのため、実験では従来手法(SGD)にSAMの2倍のエポック数を学習させることで公平に比較しています。それではSAMの実験結果を見ていきましょう!
2. SAMの実験結果
SAMでは、大きく次の3つの実験を行っています。neighborhoodサイズ$\rho$は{0.01, 0.02, 0.05, 0.1, 0.2, 0.5}からグリッドサーチをしています。ただ基本は$\rho=0.05$だそうです。
- 画像分類
- ファインチューニング
- ラベルノイズへのロバスト性
2.1 画像分類
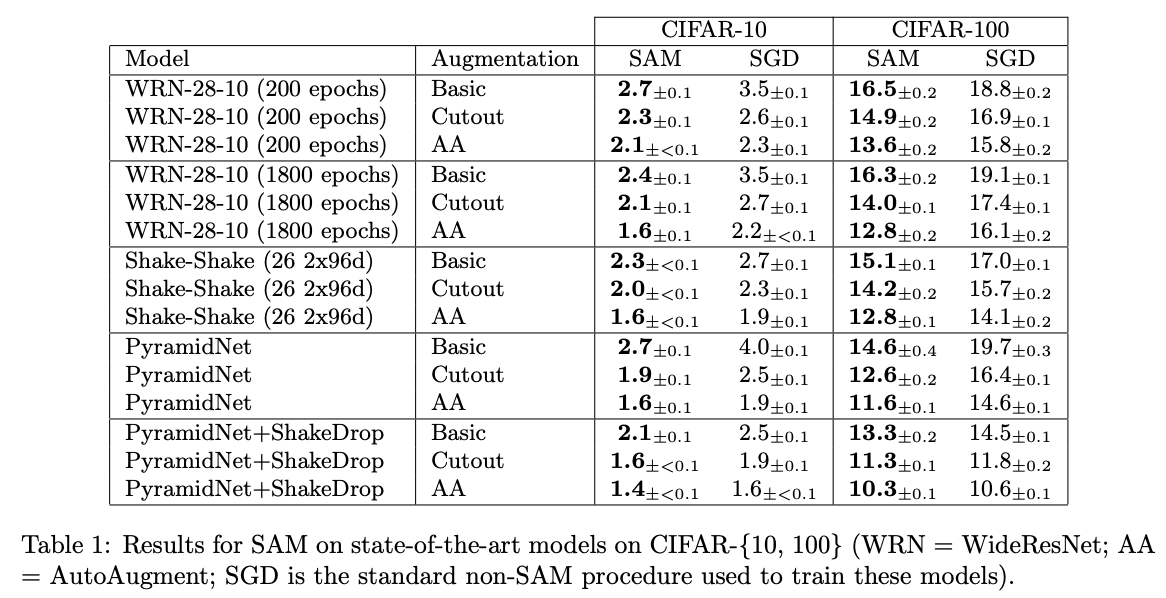
まずはCIFAR-10/CIFAR-100でのエラー率(低い方が良い)を見てみます。モデルにはWideResNetとPyramidNetを用いています。それぞれに正則化としてShake-ShakeとShakeDropも用いています。DA(=Data Augmentation)としては水平反転+ランダムクロップのBasicとCutoutとAA(=AutoAugment)の3つそれぞれを用いています。上表を見ると全てのパターンでSAMがSGDよりも高い性能を示しています。すごいですね。特にCIFAR-100はゲインが大きくPyramidNet(Basic)で5.1%もの向上を果たしています。
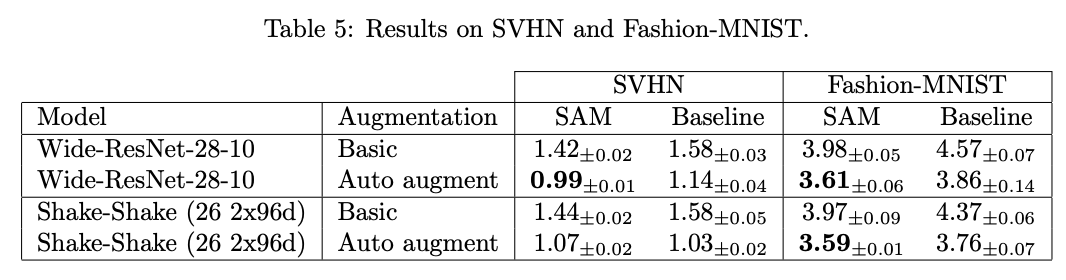
また、SVHNとFashion-MNISTに対してもWideResNetで実験を行っています。こちらでも基本的にはSAMが性能を向上させています。SVHNに至っては0.99%でSoTAを達成しています。
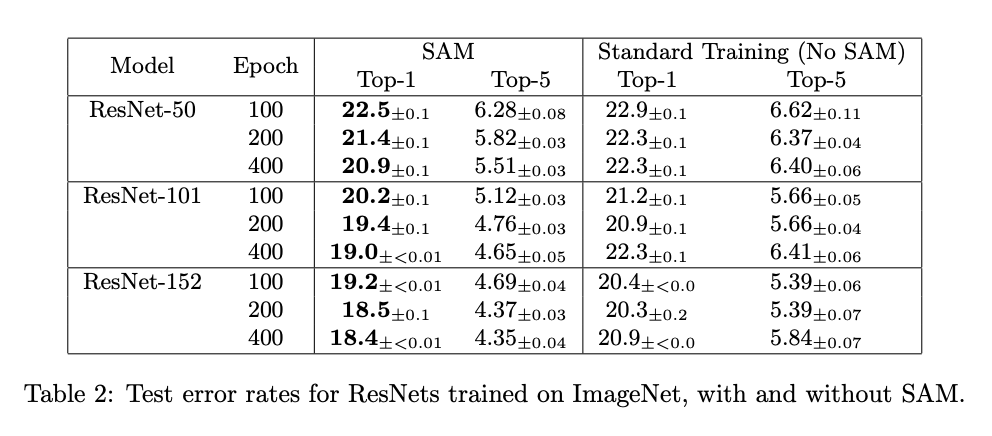
そして最後にImageNetです。ResNet-50/101/152それぞれでSAMによる性能向上が確認できますね。また、エポック数を増やすとスタンダードではオーバーフィットしているのに対して、SAMはエポック数を増やしてもオーバーフィットしていないことがわかります。
2.2 ファインチューニング
続いては、大規模データセットなどで事前学習されたSoTAモデルたちをSAMでファインチューニングしていきます。使うモデルは次の2つです。
- ImageNetで事前学習させたEfficientNet-b7
- ImageNetとラベルなしJFTで事前学習したEfficientNet-L2
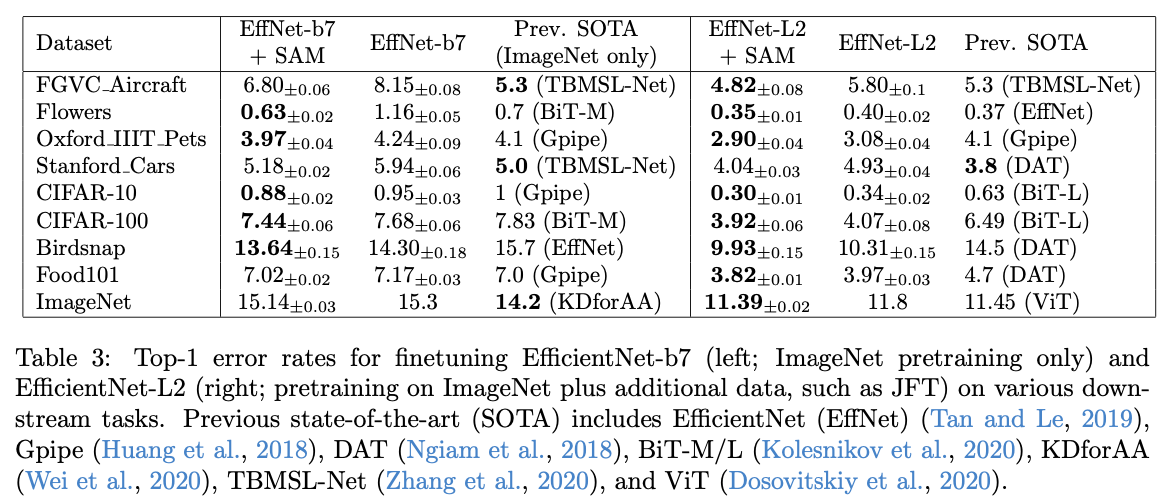
これらのモデルを各データセットでファインチューニングした結果が以下表です。
左表が1つ目のモデル(EfficientNet-b7/ImageNet事前学習)で、右表は2つ目のモデル(EfficientNet-L2/ImageNet+JFT事前学習)の結果です。左と右では事前学習に用いているデータセットがImageNetだけかどうかを分けています。右表を見るとSAMが8つのデータセットでSoTAを更新していることがわかります(前節のSVHNを加えて9つのデータセットでSoTA達成!)。CIFAR-10では0.30%、CIFAR-100では3.92%、ImageNetではなんと11.39%でViTを超えてきました。SAMの凄さがわかりますね。
2.3 ラベルノイズへのロバスト性
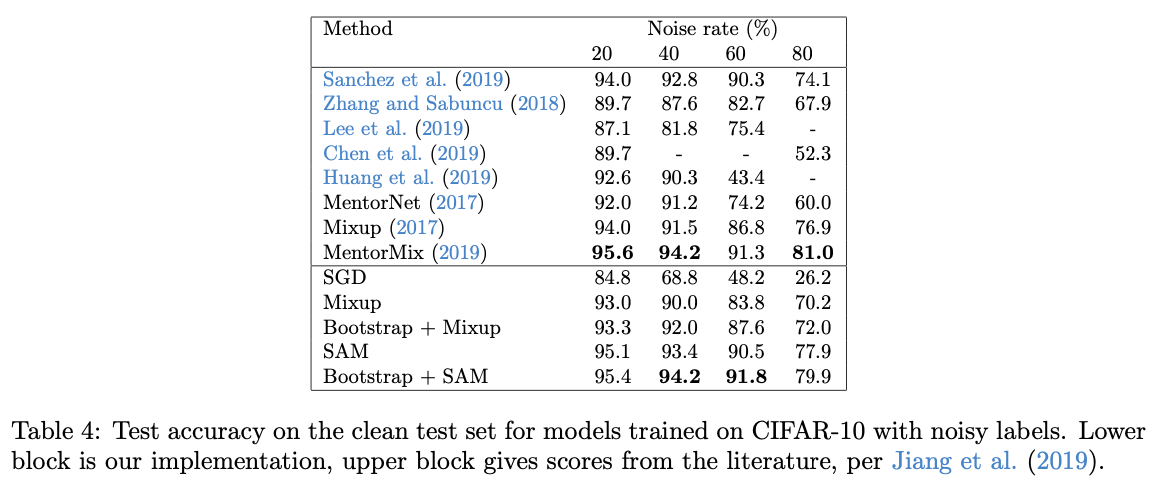
近年はモデルの汎化性能のみならず実用も考えてロバスト性も重要視されています。本論文では、学習するデータセットのラベルの一部分がランダムになっている場合で検証していきます。ResNet-32をCIFAR-10で200エポック学習させます。その時の結果が下表です。下表の上段が他論文の結果で下段が著者が再試を行った結果です。これを見ると、SAMがロバスト性専用で提案された他手法と同じような高いロバスト性を示していることがわかります。SAM恐るべしです。
3. まとめと所感
新たに提案された最適化手法SAM。その優れた汎化性能とロバスト性でSoTAを尽く更新しました。個人的には勾配を2回求めることで1点だけでなく周辺の情報も用いながら最適なパラメータを探していくというのが新鮮でおもしろかったです。今までとりあえず損失が最小となるパラメータのみを探していましたが、これからは損失の平坦さも汎化性能およびロバスト性において重要な役割を担いそうです。非公式ですが、PyTorchで簡単に試せるので早速使ってみてはいかがでしょうか!
Twitterで人工知能のことや他媒体の記事などを紹介していますので@omiita_atiimoもご覧ください。
こちらもどうぞ: