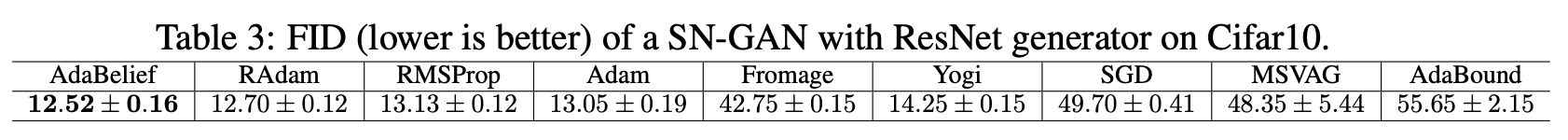オミータです。ツイッターで人工知能のことや他媒体の記事など を紹介していますので、人工知能のことをもっと知りたい方などは @omiita_atiimoをご覧ください!
他にも次のような記事を書いていますので興味があればぜひ!
出きたてホヤホヤ!最新オプティマイザー「AdaBelief」を解説!

SGD+Momentum(緑)とAdam(赤)とAdaBelief(青)の比較。青が一番早く収束していることがわかります。
"AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients", Zhuang, J., Tang, T., Ding, Y., Tatikonda, S., Dvornek, N., Papademetris, X., Duncan, J. (NeurIPS'20)
オプティマイザーとしてよく用いられるものにモーメンタム付きSGD(以下、SGD)とAdamがあります。デファクトスタンダードとしてAdamがよく用いられますが、これは必ずしもAdamがSGDよりも優れているわけではなくむしろ最終的な性能(汎化性能)はSGDのほうがAdamよりも良いことが多いです。ただ、AdamはSGDに比べ収束が速かったり安定性が高いため、とても使いやすいオプティマイザーとして人気です。そんな中、新たなオプティマイザーが**NeurIPS2020に登場しSpotlightとして選ばれました。その名も「AdaBelief」です。「"AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients", Zhuang, J., Tang, T., Ding, Y., Tatikonda, S., Dvornek, N., Papademetris, X., Duncan, J. (NeurIPS'20)」で提案された本手法は、SGDのような「高い汎化性能」とAdamのような「速い収束性」「より良い安定性」の3つを兼ね備えたオプティマイザーとして大きな期待が寄せられています。画像分類、画像生成、言語モデルでSGDやAdamなどの他手法よりも高い性能を示しています。そのうえ、アルゴリズムはAdamの一部を少し変えただけでほぼAdamなので理解も実装も簡単**です。それでは期待のAdaBeliefについて見ていきましょう!
本記事の流れ:
- 忙しい方へ
-
仕組みの解説
- Adamのおさらい
- AdaBeliefの仕組み
- なぜAdaBeliefが良いのか
- 実験結果
- まとめと所感
- 参考
原論文: "AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients", Zhuang, J., Tang, T., Ding, Y., Tatikonda, S., Dvornek, N., Papademetris, X., Duncan, J. (NeurIPS'20)
公式実装: こちら(PyTorch/TensorFlow)
0. 忙しい方へ
- AdaBeliefは高い汎化性能、速い収束性、より良い安定性の3つを兼ね備えたオプティマイザーだよ
- アルゴリズムはAdamとほぼ変わらないよ
- 勾配の予測値と実際の勾配との差でステップサイズを決定するよ
- 勾配の移動平均(=モーメンタム)を勾配の予測値としているよ
- 勾配が予測値と大きくずれていればステップサイズを小さくし、同じであればステップサイズを大きくするよ
- 画像分類/言語モデル/画像生成でAdaBeliefの優位性を示したよ
- PyTorch:
pip install adabelief-pytorch==0.1.0
from adabelief_pytorch import AdaBelief
optimizer = AdaBelief(model.parameters(), lr=1e-3, eps=1e-16, betas=(0.9,0.999), weight_decouple = True, rectify = False)
- TensorFlow/Keras:
pip install adabelief-tf==0.0.1
from adabelief_tf import AdaBeliefOptimizer
optimizer = AdaBeliefOptimizer(learning_rate, epsilon=1e-12)

SGD+Momentum(緑)とAdam(赤)とAdaBelief(青)の比較。青が一番早く収束していることがわかります。
"AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients", Zhuang, J., Tang, T., Ding, Y., Tatikonda, S., Dvornek, N., Papademetris, X., Duncan, J. (NeurIPS'20)
1. 仕組みの解説
AdaBeliefはほぼAdamです。なのでまずはAdamのおさらいをしてからAdaBeliefへと入っていきます。
1.1 Adamのおさらい
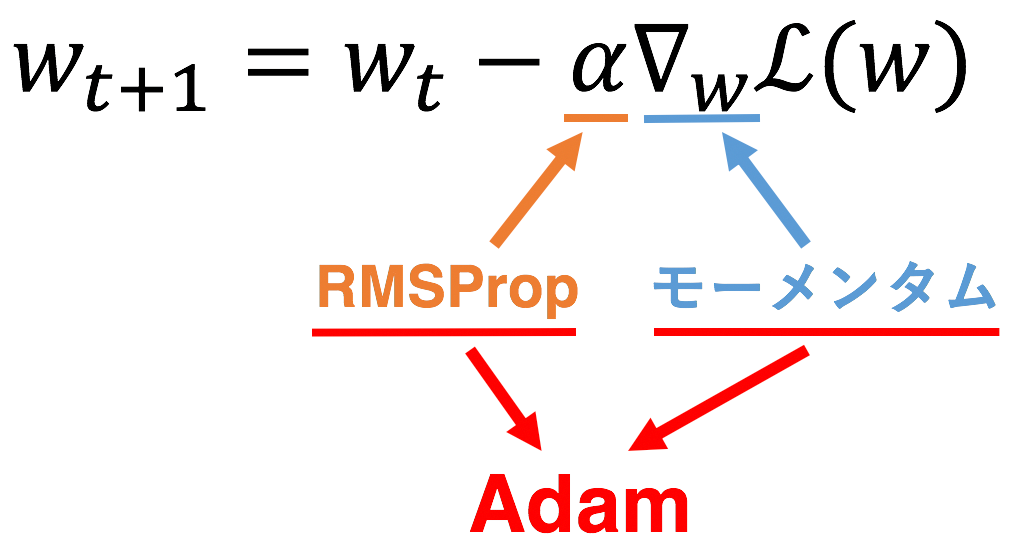
モーメンタムが勾配をいじり、RMSPropが学習率をいじるものだと考えると、Adamはこれら二つを単に組み合わせただけのものです。なのでモーメンタムとRMSPropについて簡単に触れていきます。
1.1.1 モーメンタム
モーメンタムでは、勾配の(指数平滑)移動平均を取ることでより勾配の急な変化に対しても安定してパラメータの更新ができます。式で言えば、
$$
m_t \leftarrow \beta_1 m_{t-1} + (1-\beta_1)g_t \
\theta_t \leftarrow \theta_{t-1} - \alpha m_t
$$
1つ目の式はただの移動平均でここがモーメンタムを表しています。2つ目の式は学習率$\alpha$を用いてパラメータ$\theta$を更新しているだけです。$g_t$はステップ$t$での勾配を表し、$m_t$はステップ$t$での移動平均を適用後の値を表しています。$\beta_1$は$[0,1]$の定数で、0に近ければ$m_{t-1}$が消えていきますのでステップ$t$での勾配のみを重視することになり、1に近ければ$g_t$が消えていきますので今までの勾配たちを重視するということになります。$\beta_1=0.9$がよく使われるので、実際の学習では結構過去を考慮した方が良いようですね。
1.1.2 RMSProp
一方で、RMSPropは、勾配の2乗の(指数平滑)移動平均を取りその値で学習率を割ります。これにより、勾配の小さいところなどでは更新具合を大きくし加速させることができます。つまり、RMSPropは更新のステップサイズを勾配の大きさにしたがって調整しているということです。式で表すと、
$$
v_t \leftarrow \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \
\theta_t \leftarrow \theta_{t-1} - \frac{\alpha}{\sqrt{s_t}+\epsilon}g_t
$$
この更新式を見ると$v_t$は勾配の二乗を保持していますが、パラメータ$\theta$の更新時にはルートをかけていますので、単に学習率を勾配の大きさ(の移動平均)で割っているだけであることがわかります。なので勾配が大きければ更新度合いは抑えられ、逆に小さければ更新度合いが大きくなります。$\epsilon$はゼロ除算を防ぐための非常に小さな定数で1e-8のような値が用いられます。$\beta_2$は$[0,1]$の定数でモーメンタムの時の$\beta_1$と全く同じ役割を果たします(=今を重視するか過去を重視するか)。$\beta_2=0.999$をよく見かけますので、過去を思いっきり考慮していることがわかります。
1.1.3 Adam
ここまで理解できていればAdamはとても簡単です。更新式を見てみます。(簡単のためバイアスコレクションは考慮しません。)
$$
m_t \leftarrow \beta_1 m_{t-1} + (1-\beta_1)g_t \
v_t \leftarrow \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \
\theta_t \leftarrow \theta_{t-1} - \frac{\alpha}{\sqrt{v_t}+\epsilon}m_t
$$
第一式はモーメンタム、第二式はRMSProp、そしてあとは第三式の更新式でパラメータを更新するだけです。ということで、モーメンタムとRMSPropを組み合わせたものがAdam(=Adaptive moment estimation)の正体となります。ここまでについてもっと丁寧な解説が欲しい方は拙著のこちらの記事をご覧ください。損失関数からAdamまで丁寧に解説しています。ちなみに、先にネタバレするとAdaBeliefではAdamの第二式をほんの少し変更しているだけです。それでは最後にAdamをもっとアルゴリズムっぽく表記してAdaBeliefへと移ります。
1.2 AdaBeliefの仕組み
AdaBeliefの更新式を早速見せた方がとてもわかりやすいと思います。
$$
m_t \leftarrow \beta_1 m_{t-1} + (1-\beta_1)g_t \
s_t \leftarrow \beta_2 s_{t-1} + (1-\beta_2)(g_t-m_t)^2 \
\theta_t \leftarrow \theta_{t-1} - \frac{\alpha}{\sqrt{s_t}+\epsilon}m_t
$$
上がAdaBeliefの更新式となります。ぱっと見Adamと全く同じですが、第二式のステップサイズを決定する式を見ると単なる勾配の2乗ではなく$(g_t-m_t)^2$となっています。違いはこれだけです(記号の混同を避けるために$v_t$ではなく$s_t$にしています)。これを直感的に理解するには、第一式の移動平均を考えるとわかりやすいかと思います。第一式の移動平均によって勾配の振動が抑えられるわけですが、これはつまり移動平均によってより正確な勾配の値を予測しているとも捉えることができます。移動平均を勾配の予測値と捉えることで第二式は現在の実際の勾配$g_t$とその予測値$m_t$の差で最終的なステップサイズを決定していることがわかります。この差が大きくなればパラメータを更新する際のステップサイズは($s_t$は分母にあるので)小さくなり、逆にこの差が小さければ更新する際のステップサイズは大きくなります。なので、AdaBeliefの気持ちとしては、「現在の勾配値が予測値よりも大きくずれるようであれば信用できないのでステップサイズを小さくし、あまりずれないようであれば信用に足るのでステップサイズを大きくしよう」と言えます。このBelief(=信用)を用いてAdaptive(=適応的)にステップサイズを決定しているのでAdaBeliefになるわけですね。ということで最後に先ほど同様もっとアルゴリズムっぽく示します。青字が今回のAdaBeliefにおける改良点です。次はAdaBeliefがなぜ良いのかというのを少し詳しく見ていきましょう。
1.3 なぜAdaBeliefが良いのか
論文中ではAdaBeliefの優位性をいくつかのトイプロブレムを用いて説明しています。なぜAdaBeliefが他手法よりも優れているのかということを分かりやすく理解できます。
1.3.1 AdaBeliefの優位性
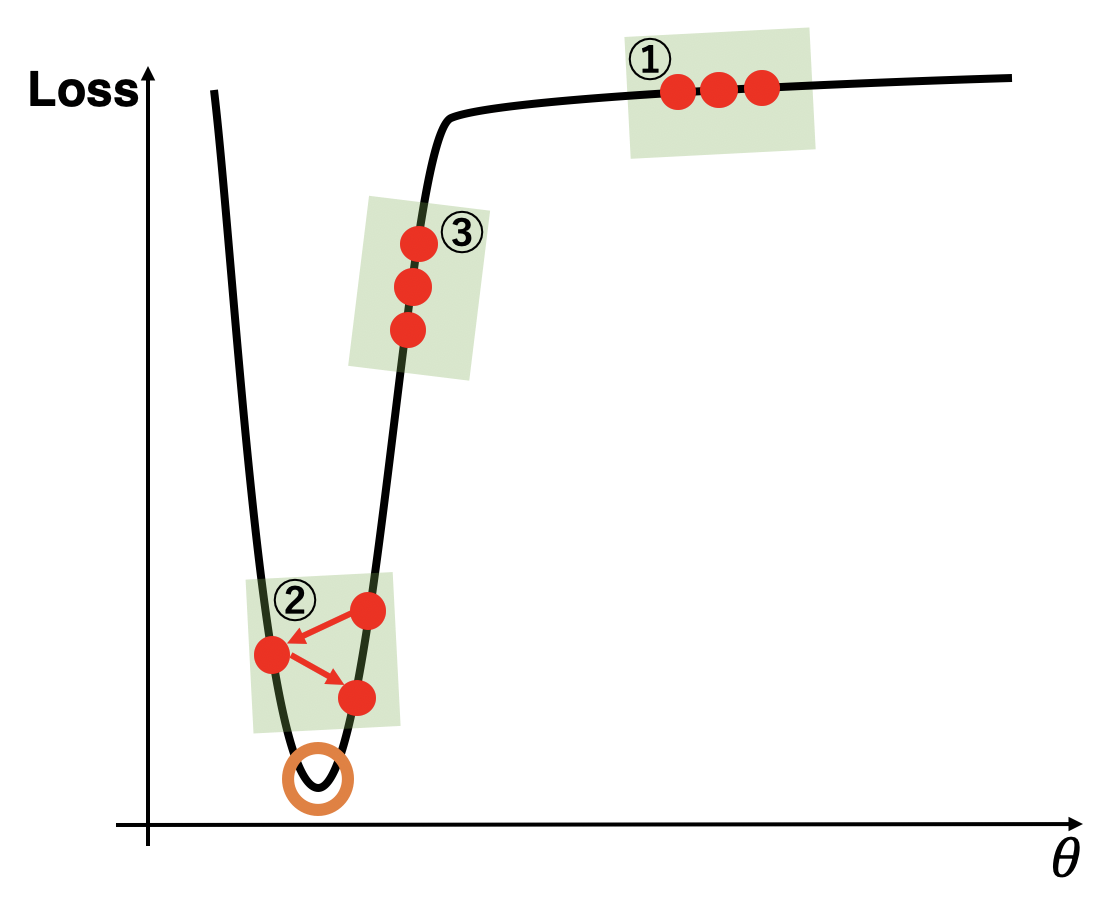
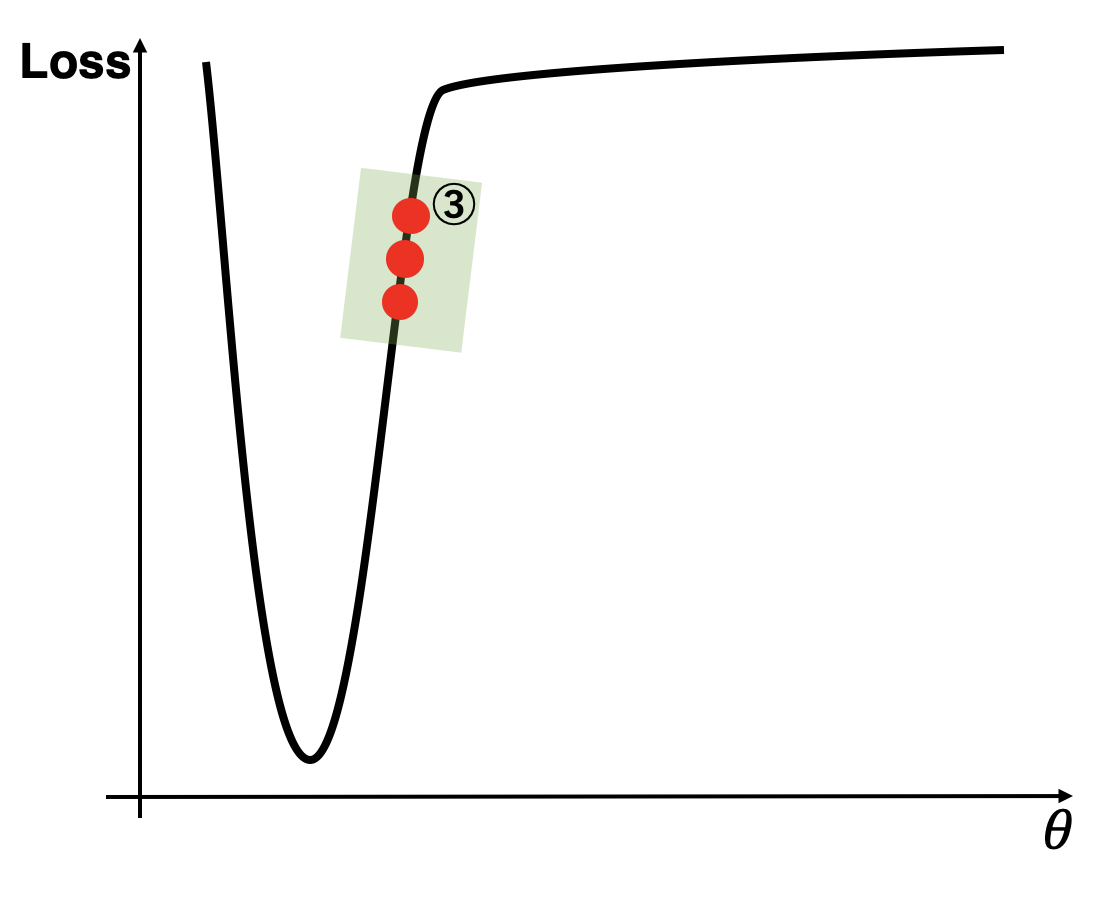
上図を用いてAdaBeliefのSGDとAdamに対する優位性を示していきます。上図においてオレンジ色で囲った最小値を目指しており、赤丸は各ステップでのパラメータとその時の損失を表しています。緑色で囲った3つの区分それぞれでAdaBeliefの良さを示します。念のためSGD、Adam、AdaBeliefの更新式を再掲します。
$$
\Delta\theta_t^{SGD} = -\alpha m_t \
\Delta\theta_t^{Adam} = -\frac{\alpha}{\sqrt{v_t}} m_t \
\Delta\theta_t^{AdaBelief} = -\frac{\alpha}{\sqrt{s_t}} m_t
$$
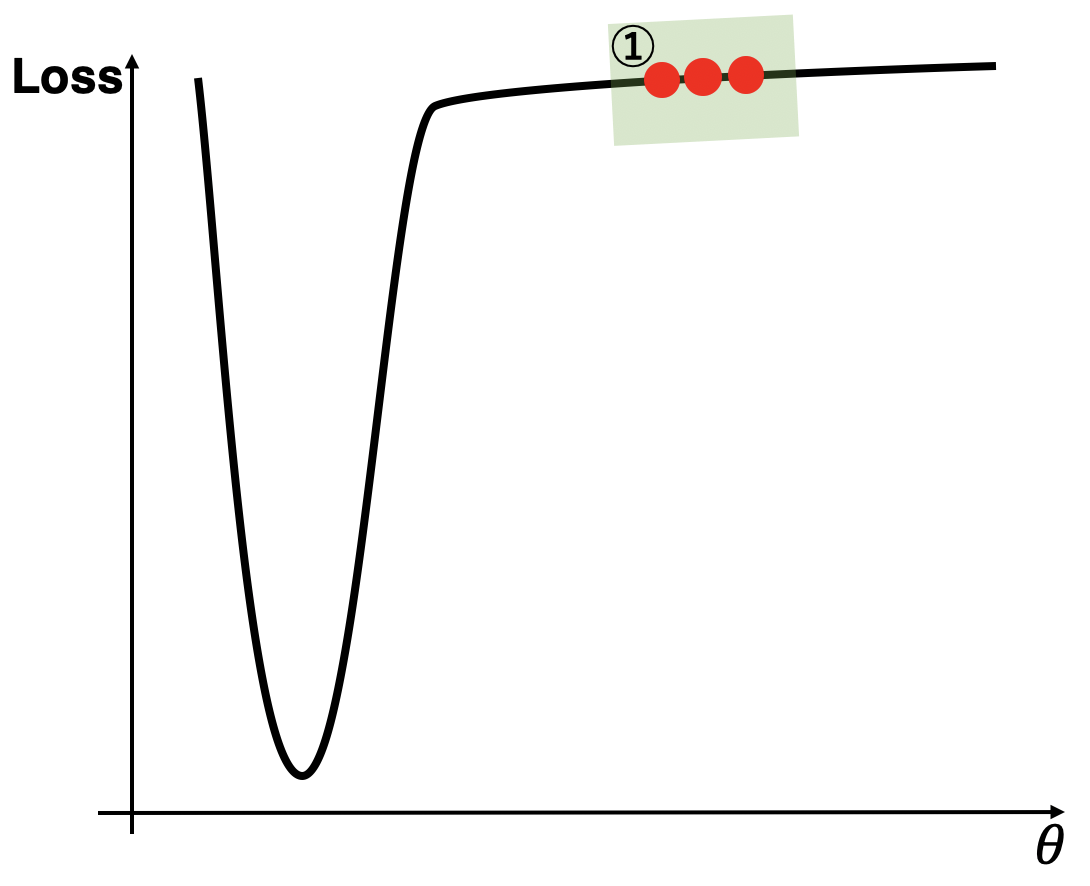
1.3.1.1 場所1の場合
まず、①について見ていきましょう。平らな①において勾配はとても小さくなってしまって進みが遅いので、理想は大きな更新をおこなって①を早く抜け出したいです。この時、SGDは単なる勾配なので更新は小さくなってしまうので良くありません。一方でAdamは勾配が小さいため$v_t$は小さくなり、その逆数となるステップサイズは大きくなるため大きな更新が行えます。また、①においていずれの勾配も大きく変動はしないため勾配の移動平均との差である$s_t$は小さくなり、AdaBeliefも①において大きな更新が行えます。まとめると、下表です。
| オプティマイザー | 更新 | 良し悪し |
|---|---|---|
| 理想 | 大 | - |
| SGD | 小 | ❌ |
| Adam | 大 | ⭕️ |
| AdaBelief | 大 | ⭕️ |
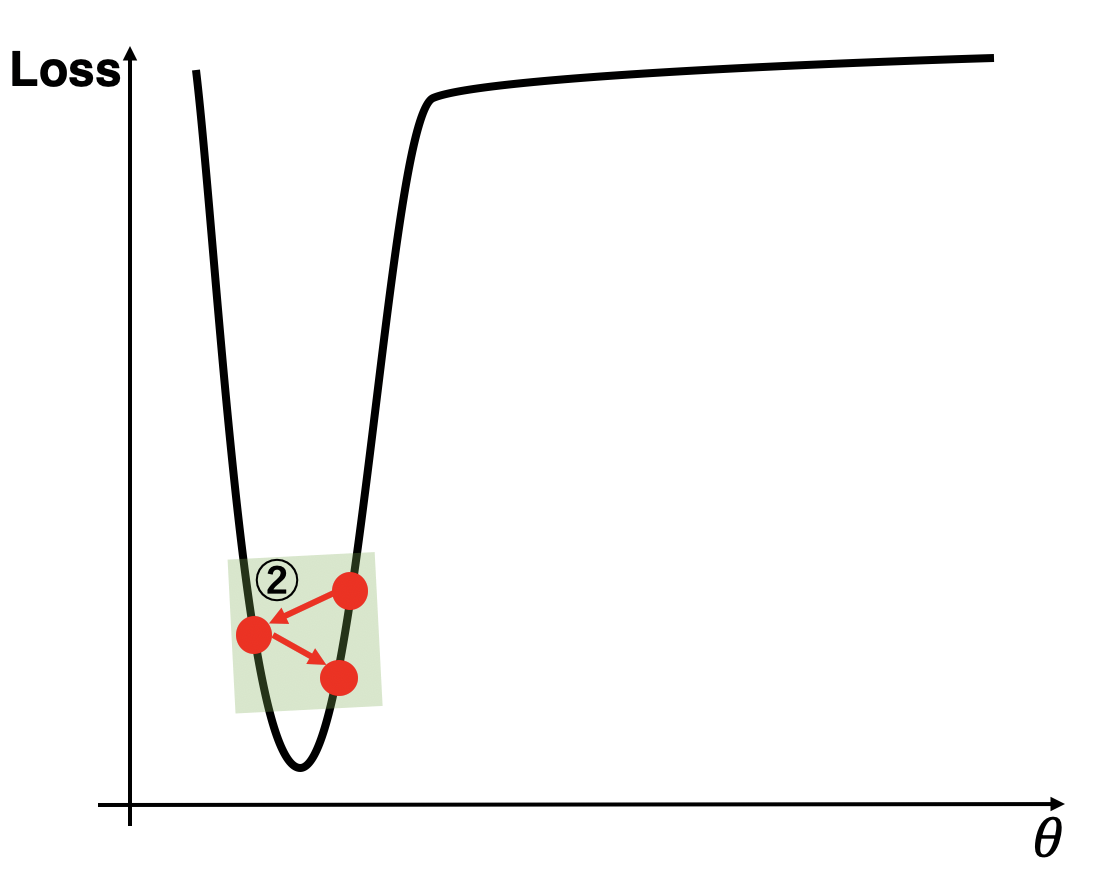
1.3.1.2 場所2の場合
続いて、②について見ていきます。ここは急峻で横幅が狭いためにオーバーシュートを起こしてしまうような場所です。そのため、このような場合、オーバーシュートを防ぐために理想の更新量は小さくあって欲しいです。まずSGDについてですが、この場所の勾配は大きいので更新も大きくなってしまい上図のようなオーバーシュートを起こしてしまいます。それではAdamではどうでしょうか。Adamは大きい勾配の逆数でステップサイズとなるので、更新は小さくなり理想通りの更新となります。そしてAdaBeliefですが、ここでのステップごとの勾配は大きく変動(オーバーシュートしているため$\theta$方向では符号がひっくり返るほどの変動)しているため、その逆数でステップサイズを決定しているのでAdaBeliefも更新は小さくなり理想通りとなります。
| オプティマイザー | 更新 | 良し悪し |
|---|---|---|
| 理想 | 小 | - |
| SGD | 大 | ❌ |
| Adam | 小 | ⭕️ |
| AdaBelief | 小 | ⭕️ |
1.3.1.3 場所3の場合
それでは、③について見ていきましょう。ここまではAdam/AdaBeliefのSGDに対する優位性を見てきましたが、ここでやっとAdaBeliefのAdamに対する優位性が見れます。傾きが急であるのが続いている③では、そのまま大きく進んでいって欲しいので理想の更新は大きいものであるはずです。SGDは、これを満たしていますね。単純に勾配が大きいので更新も大きくなります。一方でAdamについてですが、Adamは大きな勾配の時はいつでもステップサイズを小さくしてしまうため、更新は小さくなってしまいスピードダウンしてしまいます。しかし、AdaBeliefはここをちゃんと改良できていて、③において勾配の変動はなく常に一定の方向を向いているため、$s_t$は小さくなりステップサイズは大きくなってくれます。AdaBeliefがAdamよりも優れているパターンが出てきてくれました。
| オプティマイザー | 更新 | 良し悪し |
|---|---|---|
| 理想 | 大 | - |
| SGD | 大 | ⭕️ |
| Adam | 小 | ❌ |
| AdaBelief | 大 | ⭕️ |
ということで、上記3パターン全てにおいて理想の更新を示しているのはAdaBeliefだけということになりました。これを元に続いては具体的な関数でも見てみます。
1.3.2 実際の関数上での比較
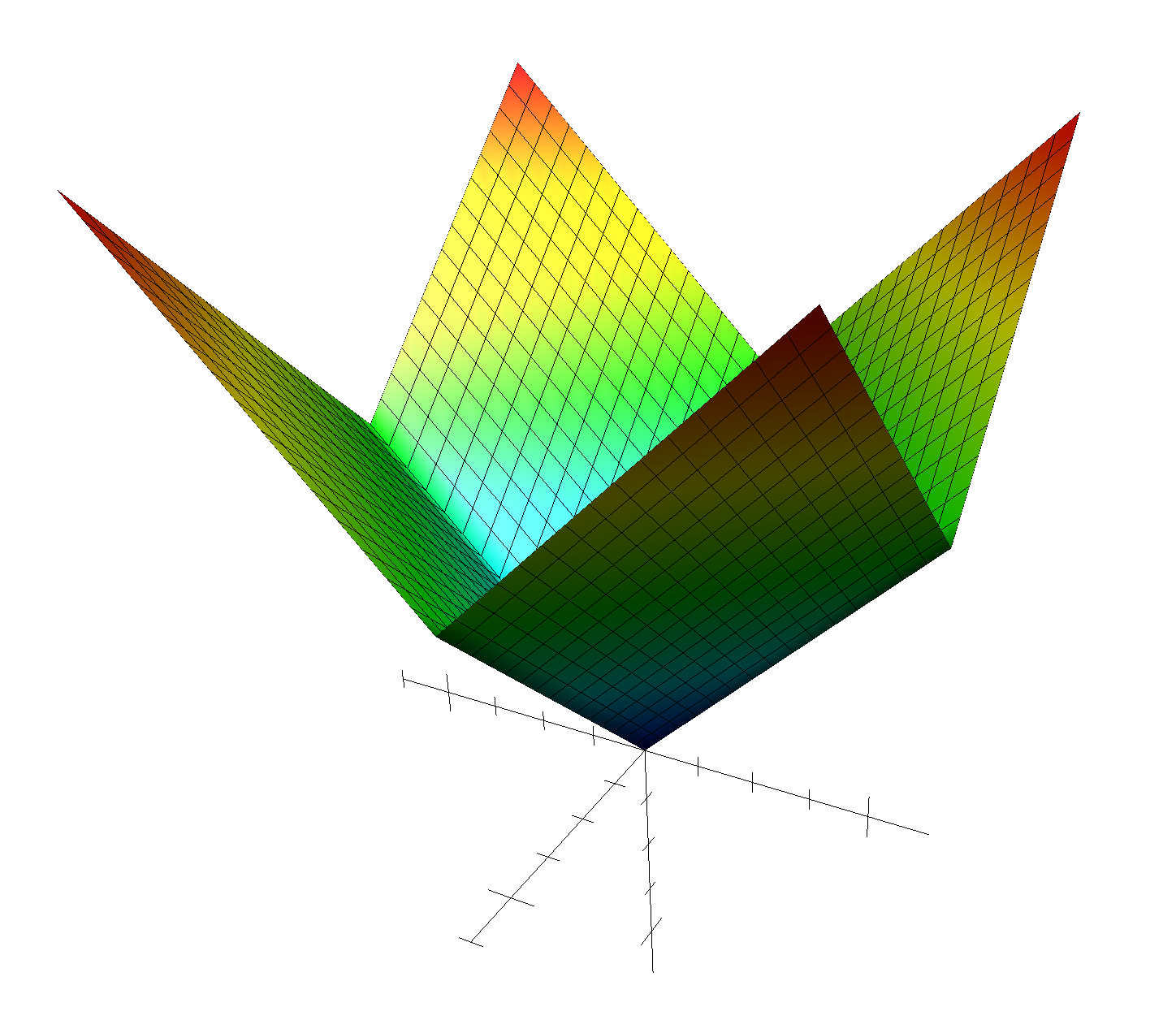
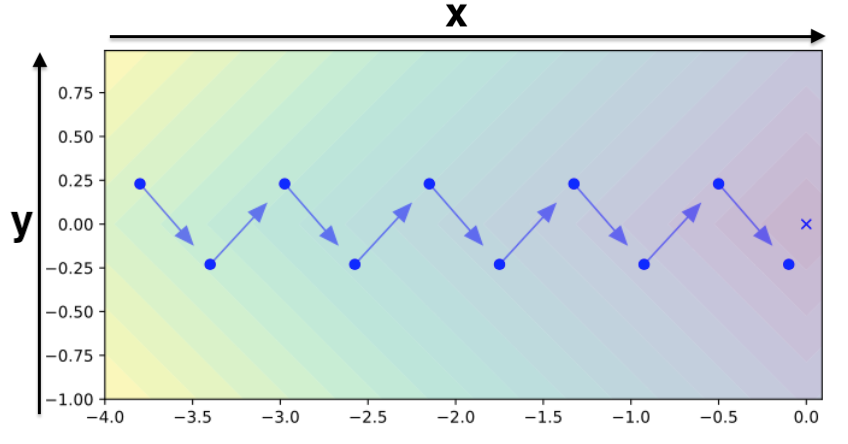
ここでは上図を用います。上図は関数$f(x,y)=|x|+|y|$なのですが、ぱっと見よくわかりづらいです。$f(x,y)=|x|+|y|$は3Dで表すと下図のようになります。
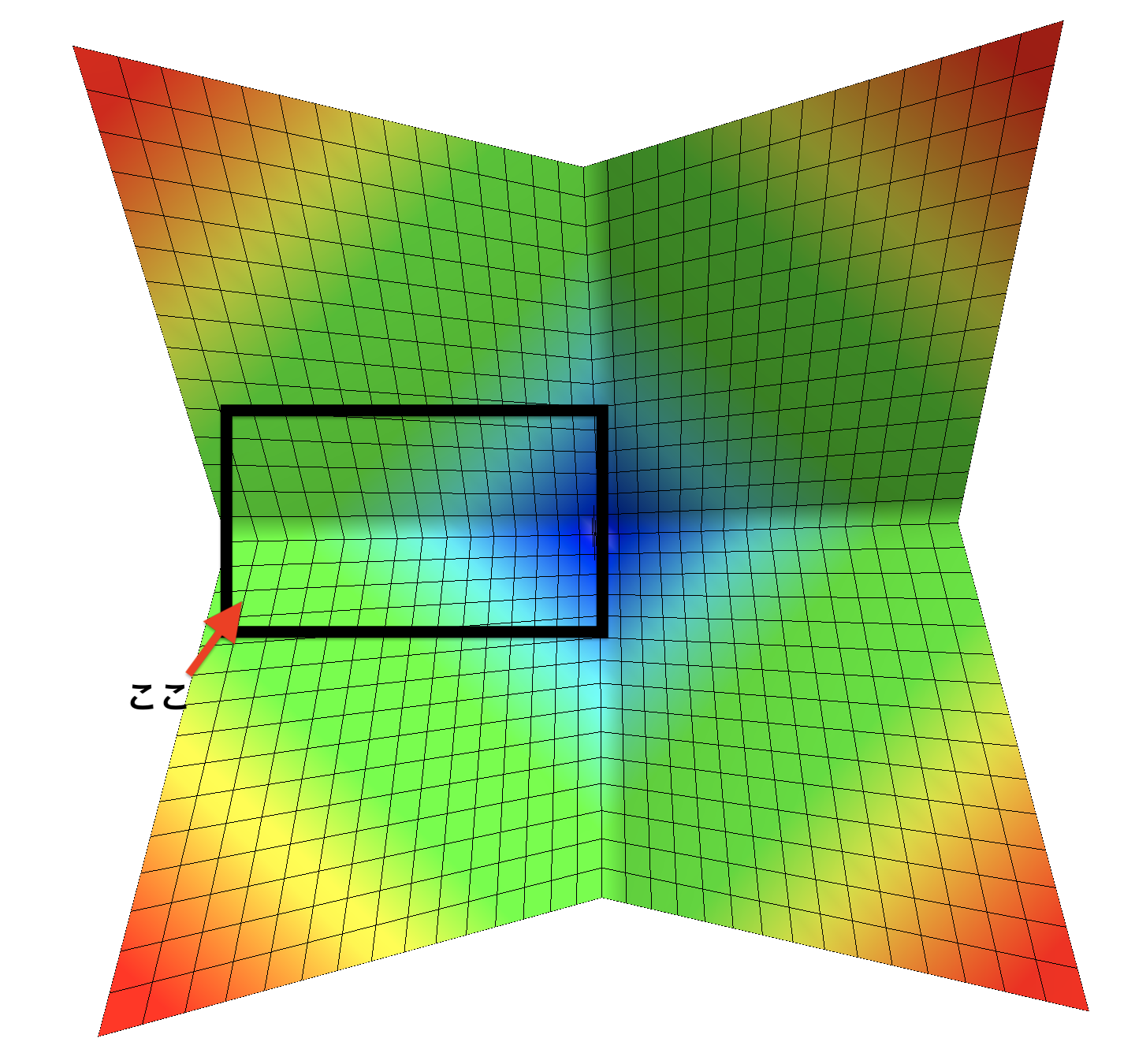
これを真上(z軸上)から見下ろしてみましょう。
ここです。ここを見ると、先ほど見た図になるということです。
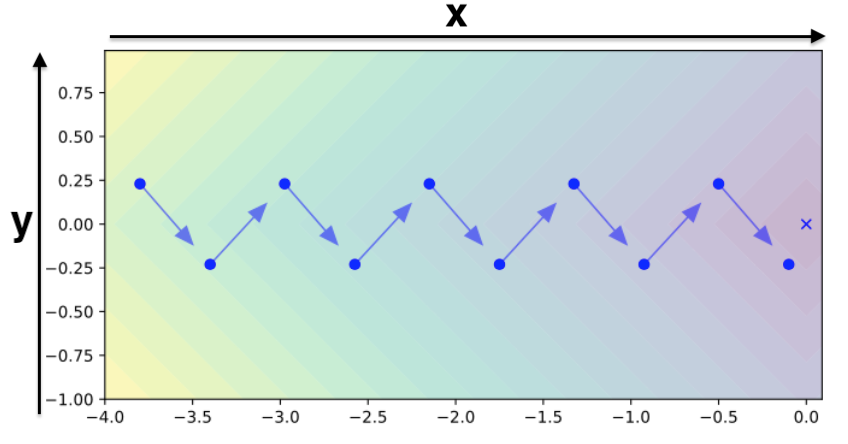
3Dの図が頭に入っていれば上図はわかりやすいと思います。右にある青バツがゴールである最小値を示しています。ここで$f(x,y)=|x|+|y|$を採用しているのは、全箇所で勾配は1か-1のいずれしか取らないので分かりやすいためです。実際に上図の青矢印に則って各ステップでのx方向、y方向の勾配を表すと、
| Step | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $g_{t,x}$ | 1 | 1 | 1 | 1 | 1 |
| $g_{t,y}$ | -1 | 1 | -1 | 1 | -1 |
となります。x軸は一定で1ですが、y軸方向は1と-1を行ったり来たりしています。この時、Adamの$v_x$と$v_y$ はどうなるかというと、勾配の大きさの移動平均なので次のように全て1となります。つまり、Adamにおいてはx軸もy軸も同じ大きさの勾配となるため、全体の勾配は45度を向いて上図のようなジグザグを作ってしまうということです。
| Step | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Adam | $v_{t,x}$ | 1 | 1 | 1 | 1 | 1 |
| $v_{t,y}$ | -1 | 1 | -1 | 1 | -1 |
一方でAdaBeliefの$s_x$と$s_y$ がどうなるかですが、勾配の移動平均を勾配の期待値であると仮定(移動平均は良かれ悪かれ勾配を予測しているものなので直感的にもこの仮定は納得できます。)をまず置きます。そうすると、少し式変形をすると、$s_t$は$g_t$の分散と同義であることが導けます。このことを用いると、x方向には変化がないので$s_{t,x}=0$となり、y方向は分散が1なので$s_{t,y}=1$となります。表で表せば下表です。これによって、$s_{t,x}\lt s_{t,y}$ が実現されx方向にだけ思いっきり進む勾配が完成します。つまり、y方向の振動を許さないくらいx軸に進んでくれるということです。AdaBeliefがAdamよりも優れているところがまた1つ分かりましたね。
| Step | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| AdaBelief | $s_{t,x}$ | 0 | 0 | 0 | 0 | 0 |
| $s_{t,y}$ | 1 | 1 | 1 | 1 | 1 |
最後に他の関数たちでのAdaBeliefの優位性をアニメーションで見ます。文字が小さくて見づらいかもしれませんが、"モーメンタム付きSGD"(緑色)と"Adam"(赤色)と"AdaBelief(青色)"を比べています。下図では計6つの関数の例で、それぞれの2次元平面および3次元でのパラメータの進み方を示しています。いずれの関数でもAdaBelief(青色)が一番早く収束していることがわかります。ちなみに上段左は先ほど例にとった$f(x,y)=|x|+|y|$で、AdaBeliefが一番早く収束していますね。

2. 実験結果
画像分類、言語モデルそして画像生成の3つでで他オプティマイザーとの性能比較を行なっています。それぞれのデータセットは以下のようになっています。
-
画像分類:
- CIFAR-10
- CIFAR-100
- ImageNet
-
言語モデル:
- Penn TreeBank
-
画像生成:
- CIFAR-10
それではそれぞれの結果について見ていきましょう。
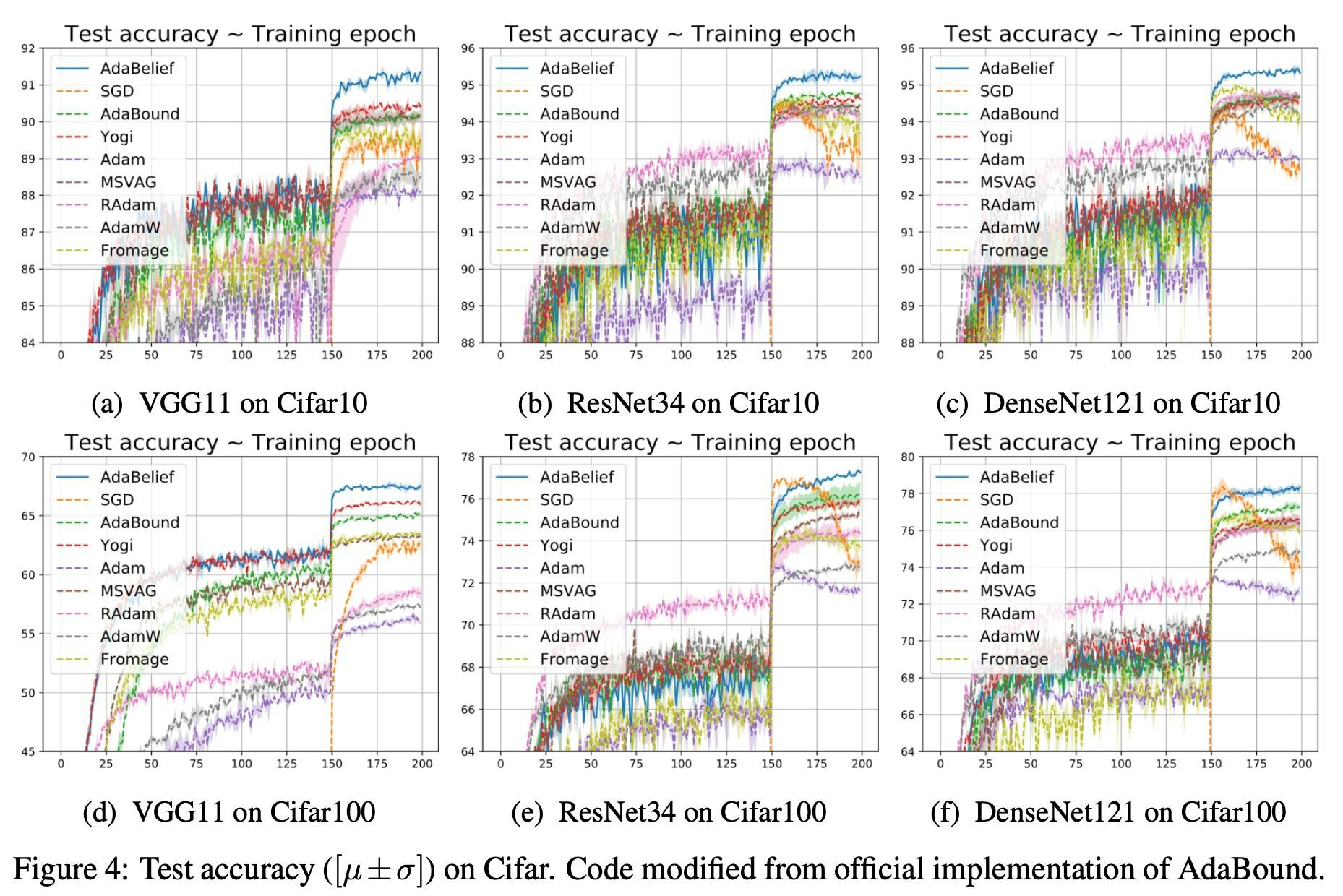
2.1 画像分類
まずはCIFAR-10/CIFAR-100について見ていきます。エポック数は200でモデルはVGG11/ResNet34/DenseNet121を用いています。上図はそれぞれのテストデータに対する精度を示しており、上段(a,b,c)がCIFAR-10で下段(d,e,f)がCIFAR-100です。エポック150で精度のジャンプがあるのは、そこで学習率を$\frac{1}{10}$に落としているからです。DenseNet121(CIFAR-100)が橙色のSGDと拮抗していますが、それ以外はいずれにおいても青色のAdaBeliefが頭ひとつ抜けていますね。これは単純にすごいです。
続いて、ImageNetについてです。実験にはResNet18を用いています。エポック数は90です。ここで、画像認識をやっている方だと「なぜResNet18?普通ImageNetの性能評価ならResNet50ではなくて?」と思う方もいるかもしれませんが、ここに関しては論文著者の計算リソースが足りないために小型のResNet18を用いているようです(Redditの書き込みより)。上表を見ると、AdaBeliefがSGD以外の他手法を見事に打ち負かしています。ただし、SGDにはやや負けています。やはり汎化性能ではSGD強敵ですね。これを論文著者は「Adaptive系手法とSGDとの汎化性能の差を縮められた!」とポジティブに捉えています。(AdaBeliefがSGDに負けているのに太字にしているのは少しセコい感じもしますが笑)
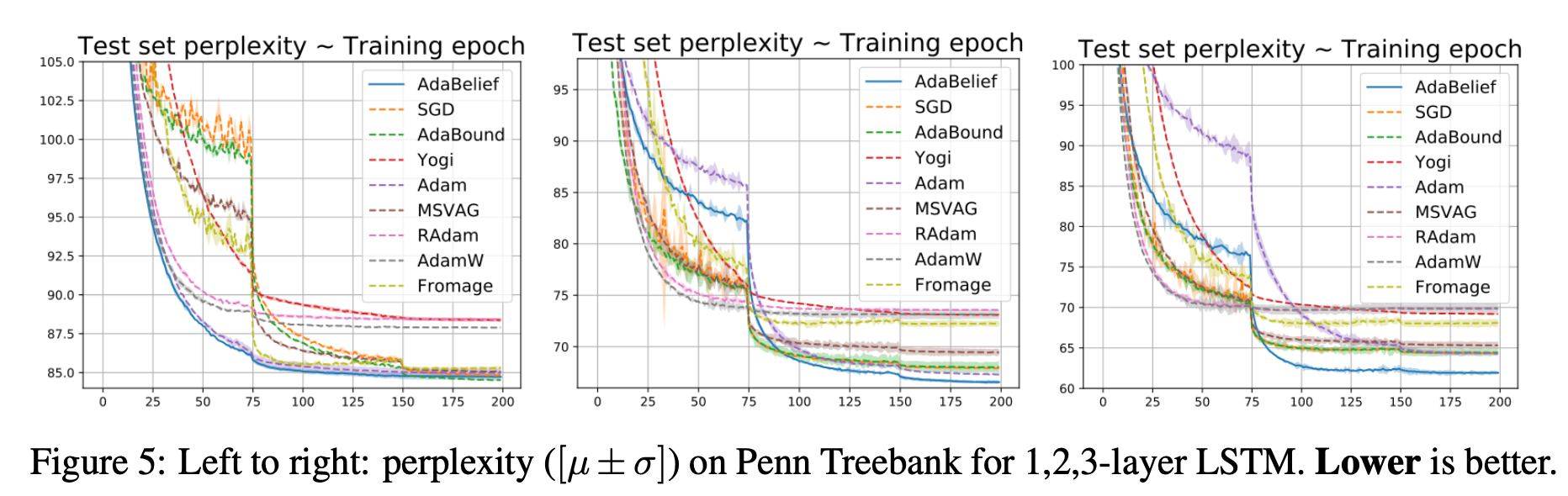
2.2 言語モデル
上図はPenn TreeBankデータセットにおける言語モデルのパープレキシティ(小さい方が良い)を示しています。左からそれぞれ1/2/3層LSTMを用いた場合を示しています。見えづらいですが、一方で1層LSTMではAdaBoundにわずかに負けてしまっています。ただ、2層LSTM(中央)と3層LSTM(右)の時に他手法よりも大きな差で高い性能を示していますね。
ちなみに、言語モデルではないですがGithubでTransformerによる翻訳の結果も1つだけ示しており、下表のようにAdaBeliefがAdamWとRAdamに勝っています。
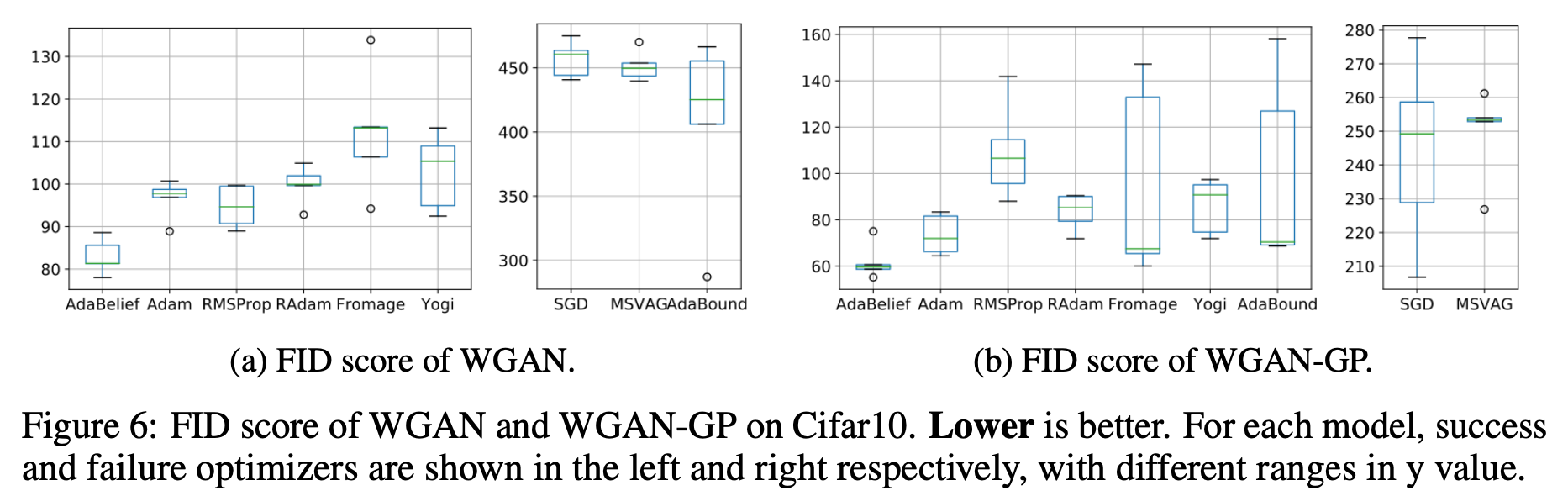
2.3 画像生成
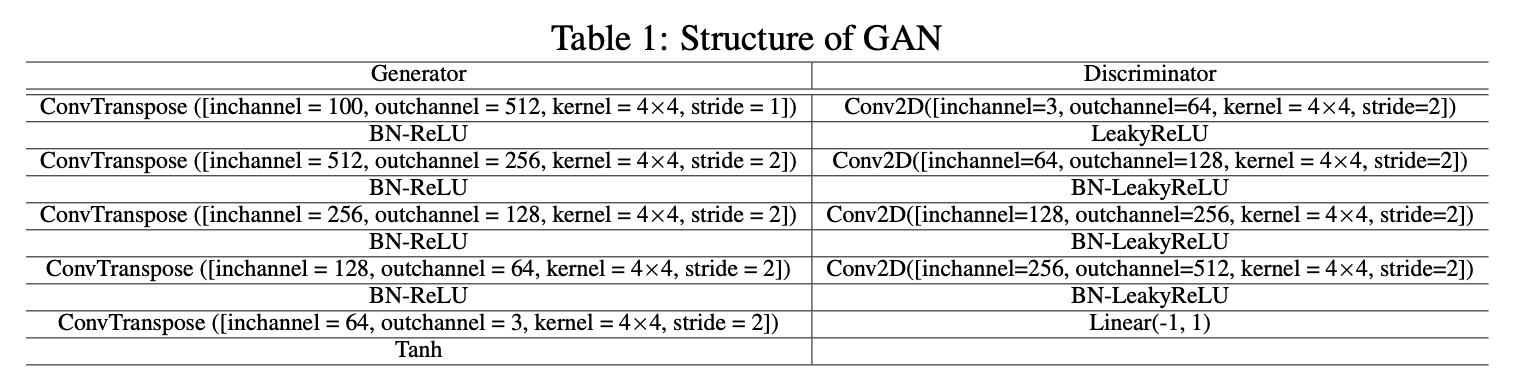
最後にGANを用いた画像生成です。画像生成においてもオプティマイザーの性能を比較しているというのが個人的に新鮮です。これによってオプティマイザーの安定性を示しているようです。データセットはCIFAR-10でモデルはWGAN(上図a)とWGAN-GP(上図b)を用いています。FIDは低い方がいいので、画像生成においてもAdaBeliefが一番良いことがわかります。
ついでにPadamと呼ばれる手法とも比較しています。上表がその結果です。PadamはSGDとAdamの中間のようなもので、Adamの更新式が$\theta_{t+1}=\theta_t-\frac{\alpha}{v_t^p} m_t$になっているだけです。この式の通りハイパーパラメータ$p$によってAdam感を強めるのかSGD感を強めるのかを調整しています。$p=\frac{1}{2}$でAdam、$p=1$でSGDとなります。PadamのいずれのハイパーパラメータでもAdaBeliefが一番FIDが低いですね。ImageNetは識別精度になっていますが、PadamがSGDっぽく($p<\frac{1}{8}$)なるとAdaBeliefと拮抗するのがわかります。ちなみにここまでの実験で用いているGANのアーキテクチャは以下になります。Spectral Normは使っていない簡潔なアーキテクチャであるためにFIDが全体的に高めになっています。
SNGANについての実験も示しており、それではしっかりと低いFIDでAdaBeliefが一番良いですね。(RAdamとは結構僅差ですが。)
3. まとめと所感
画像分類、言語モデル、画像生成で優位性を示したAdaBelief。汎化性能、収束性、安定性の3つを兼ね備えた期待のオプティマイザーとしてこの先どれほど使われるようになるかとても気になります。使い方も非常に簡単で、PyTorchだと
pip install adabelief-pytorch==0.1.0
from adabelief_pytorch import AdaBelief
optimizer = AdaBelief(model.parameters(), lr=1e-3, eps=1e-16, betas=(0.9,0.999), weight_decouple = True, rectify = False)
これであとは通常のオプティマイザーと同様に使えます。TensorFlowも同様に以下です。
pip install adabelief-tf==0.0.1
from adabelief_tf import AdaBeliefOptimizer
optimizer = AdaBeliefOptimizer(learning_rate, epsilon=1e-12)
各タスクに対する詳しいハイパーパラメータなどもGithubでまとめてくれているのでそちらも参照しながら、ぜひ試してみてください!
Twitterで人工知能のことや他媒体の記事などを紹介していますので@omiita_atiimoもご覧ください。
こちらもどうぞ: