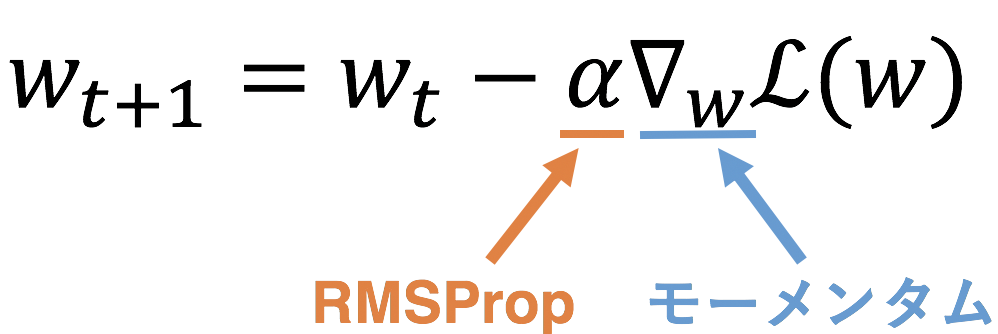オミータです。ツイッターで人工知能のことや他媒体で書いている記事など を紹介していますので、人工知能のことをもっと知りたい方などは気軽に@omiita_atiimoをフォローしてください!
【決定版】スーパーわかりやすい最適化アルゴリズム
深層学習を知るにあたって、最適化アルゴリズム(Optimizer)の理解は避けて通れません。
ただ最適化アルゴリズムを理解しようとすると数式が出て来てしかも勾配降下法やらモーメンタムやらAdamやら、種類が多くあり複雑に見えてしまいます。
実は、これらが作られたのにはしっかりとした流れがあり、それを理解すれば 簡単に最適化アルゴリズムを理解することができます 。
ここではそもそもの最適化アルゴリズムと損失関数の意味から入り、最急降下法から最適化アルゴリズムの大定番のAdamそして二階微分のニュートン法まで順を追って 図をふんだんに使いながら丁寧に解説 していきます。
それでは早速最適化アルゴリズムとは何なのかを見てみましょう!
読んで少しでも何か学べたと思えたら 「いいね」 や 「コメント」 をもらえるとこれからの励みになります!よろしくお願いします!
(細かい厳密性よりも理解のためのわかりやすさを優先しているので論文のような厳密性を求めている場合は最適化アルゴリズムたちの原論文を当たっていただけますようお願いします。)
Image Credit: Alec Radford
0. 忙しい方へ
- 最急降下法: 全データ を使って損失関数が最小値になるように、勾配を使ってパラメータ更新するよ。
- SGD: データ1つだけ をサンプルして使うことで、最急降下法にランダム性を入れたよ。
- ミニバッチSGD: データを16個とか32個 とか使うことで並列計算できるようにしたSGDだよ。
- モーメンタム: SGDに 移動平均 を適用して、振動を抑制したよ。
- NAG: モーメンタムで損失が落ちるように保証してあるよ。
- RMSProp: 勾配の大きさに応じて 学習率を調整 するようにして、振動を抑制したよ。
- Adam: モーメンタム + RMSProp だよ。今では至る所で使われているよ。
- ニュートン法: 二階微分 を使っているので、ものすごい速さで収束するよ。ただ計算量が膨大すぎて 実用されていない よ。
1. 最適化アルゴリズムとは?
SGDやらモーメンタムやらAdamやら色々な最適化アルゴリズムを聞きますが、
これらの最適化アルゴリズムは全て最急降下法の派生で、最急降下法さえ理解すれば他の最適化アルゴリズムは理解できてしまう のです。
ニューラルネットワークをはじめとした全ての機械学習で到達したいゴールは何でしょうか。
それは、極端に言えば、損失をゼロにする ということです。「損失をゼロにする」というゴールをなるべく効率よく到達してくれるものが最適化アルゴリズム です。
そのことについて詳しく説明していきます。
1.1 そもそも損失とは?
そもそも 損失とはニューラルネットワークによる予測値と正解値との差 のことです。そのため、ニューラルネットワークの予測値が変われば、損失も変わります。そのニューラルネットワークの予測値はパラメータ(重みおよびバイアス)で変化します。つまりこの損失を小さくするには、 ニューラルネットワークが正解値を出すようにのその中のパラメータたちの値をいろいろとイジくる、のです。その パラメータというのはニューラルネットワークの重みとバイアスのこと ですね。以下の式でいうと$w$と$b$ですね。$a$ は任意の活性化関数(SigmoidとかReLUとか。)です。
y = a(wx+b)
そうすると次の問題が出てきますね。それはニューラルネットワークのパラメータをどういじればいいのか、ということです。その前にさらなる理解のために少し損失とニューラルネットワークについて数式で見てみましょう。
繰り返しになりますが、 損失は予測値と正解値の差 なので式で表すと、1つのデータに対して損失は以下のようになります。
\mathcal{L} = (y - \hat{y})^2
ここで $y, \hat{y}$ はそれぞれ正解値とニューラルネットワークによる予測値です。2乗にしているのは単純に損失の符号を正にするため です。(この二乗誤差は特にMSE(Mean Squared Error)と言われます。)
1.2 損失とニューラルネットワーク
ニューラルネットワークは入力に対して出力を出すので、ニューラルネットワークを関数$f$と見ると、予測値 $\hat{y}$ は入力データ$x$に対するニューラルネットワーク $f$ の出力なので、$\hat{y} = f(x)$ と表せることがわかります。
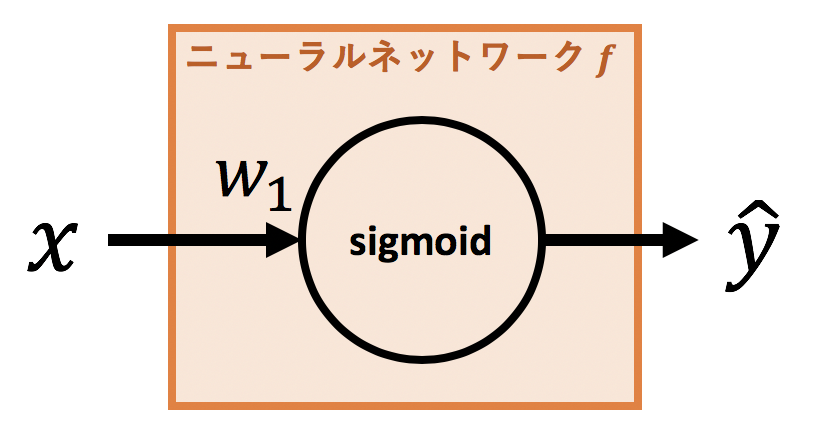
ニューラルネットワークをもう少し具体的に定義してみましょう。ここではsigmoid関数を活性化関数とする1層のニューラルネットワークを使います。わかりやすさのためバイアス $b$ は除きます。図で表すと以下になります。
数式で表せば、
f(x) = \mathrm{sigmoid}(w_1x) =\frac{1}{1+e^{-w_1x}}
となるので、先ほどの損失 $\mathcal{L}$ の式は以下のように表せます。
\mathcal{L} = (y - \hat{y})^2 = (y - \frac{1}{1+e^{-w_1x}})^2
ここで入力データ $x=2$, 正解値 $y=1$ のデータがあったとすると上式はパラメータ $w_1$ (重み)、の関数として見ることができます。つまり、
\mathcal{L(w_1)} = (1 - \frac{1}{1+e^{-2w_1}})^2
= 1-\frac{2}{1+e^{-2w_1}}+\frac{1}{1+2e^{-2w_1}+e^{-4w_1}}
これが損失関数で、この損失関数が最小値を取るように $w$ をいじくれば、結果的に最高のパラメータ $w$ を持ったニューラルネットワークが獲得できそうです 。
つまり、損失関数が最小値を取るようなパラメータを求めればいいのです。
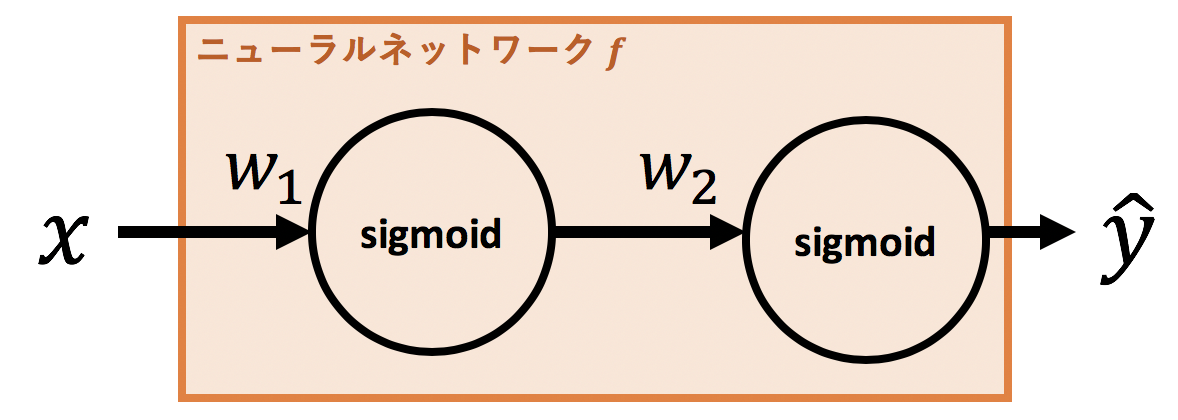
次に図で理解してみます。今度はニューラルネットワークが2つのパラメータ$w_1, w_2$を持っているとします。図で表せば以下のようなニューラルネットワークです。
これを数式で表すと、
f(x) = \sigma(w_2\sigma(w_1x))
ここで $\sigma(\cdot)$ はsigmoid関数のことです。この$w_1, w_2$の値を色々と調整することでニューラルネットワークによる予測値が変わっていきます。適当にいじると、予測値が正解値に近づき損失が小さくなったり、はたまた予測値が正解値からずれ損失が大きくなったりします。先ほど同様、入力データ $x=2$, 正解値 $y=1$ のデータでの損失関数は以下になります。
\mathcal{L(w)} = (1 - \sigma(w_2\sigma(w_1\cdot2)))^2
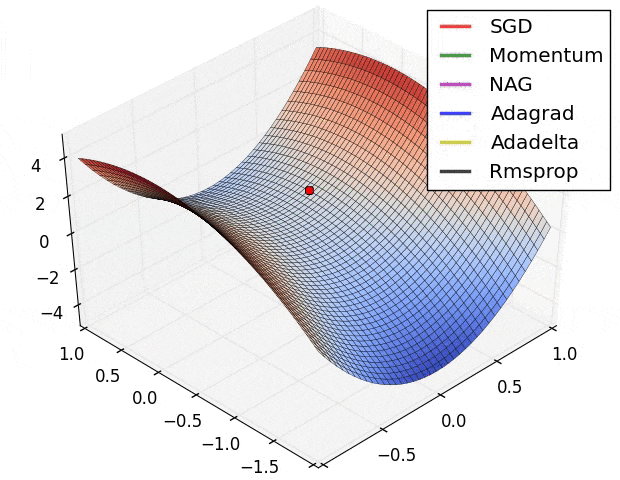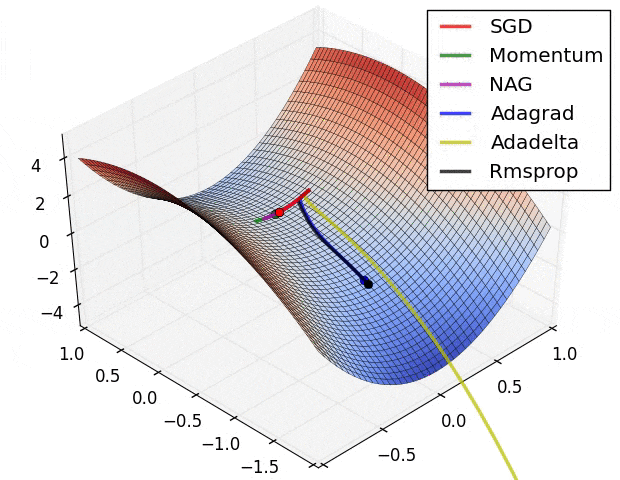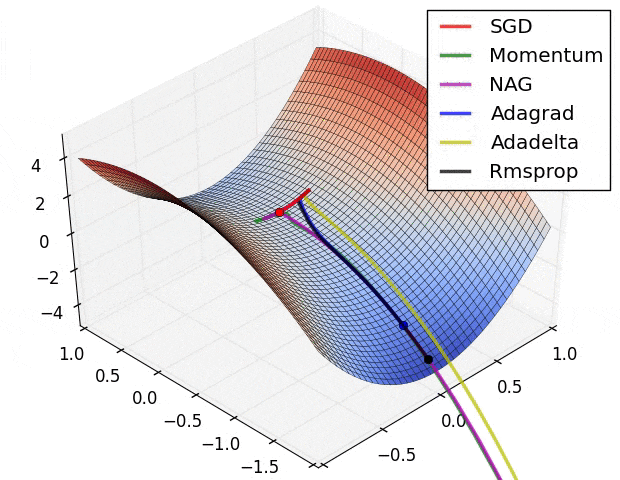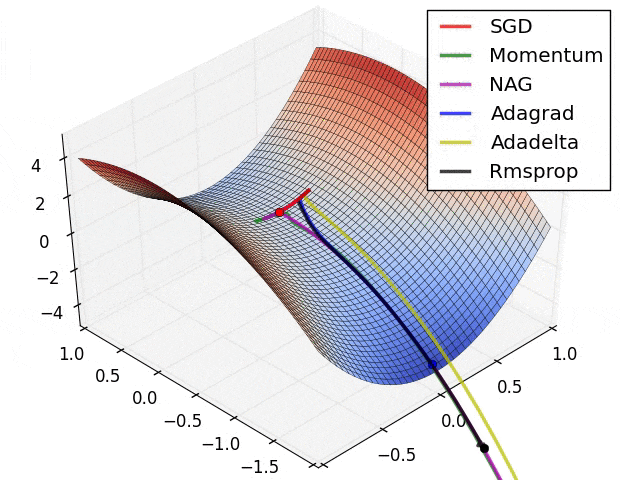
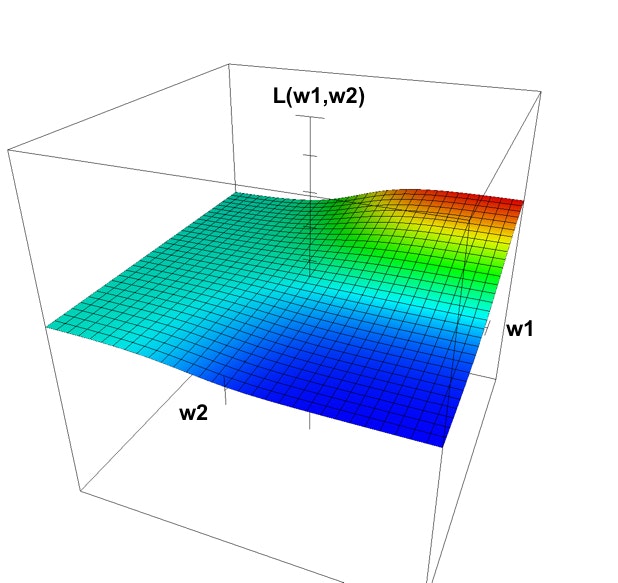
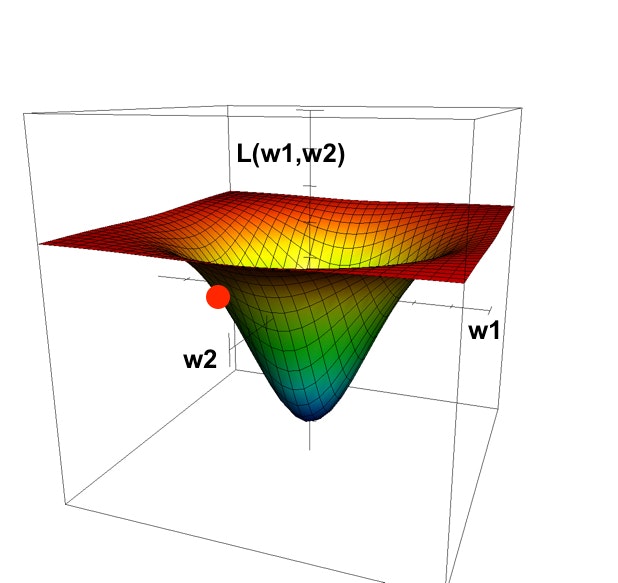
これを $w_1, w_2, \mathcal{L}(w)$ を軸とするグラフで表すと下図のようになります。
損失を小さくすればいいわけですから、図の中で一番小さい損失値(青い部分)をとるパラメータ $w_1, w_2$ がこのニューラルネットワークが獲得したいパラメータの値 です。この最適なパラメータをなるべく効率的に獲得してくれるものこそが最適化アルゴリズム なのです。
1.3 損失と最適化アルゴリズム
さて、ここまでで最適な $w_1, w_2$ を獲得することの意味を理解できたかと思います。では具体的にニューラルネットワークはどうやってその最適なパラメータを獲得するのでしょうか。
ここで出てくるのが微分 です。
微分は関数のある点での傾きがわかる という優れものでしたね。ニューラルネットワークでは、その優れた性質を持つ微分を何度も繰り返しトライアル&エラーで最適なパラメータを獲得します。
でも、「微分なんか言うまどろっこしい方法を使わなくても上のグラフを見ればパッと最小値がわかるから、上のようなグラフを書いて最小値を取る値を最適な $w_1, w_2$ とすればいいじゃないか」、と思ってしまいそうです。
ただ、よく考えてみてください。このグラフを獲得するには、損失関数にいろんな組み合わせの $w_1, w_2$ を大量に代入してみて、それぞれで値を求めて大量にプロットしていくことで上のようなグラフが書けます。その色々な値を大量に計算するというのは要はブルートフォースで全く賢くありません。上のグラフのような2次元($w_1, w_2$)しかパラメータがないなら、なんかできそうと思う方もいるかもしれませんが、実際の最近のニューラルネットワークのパラメータ数は2次元どころではなく、1000万以上ものパラメータがあることが珍しくありません。もはや1000万の数字の組み合わせから損失を1つ計算するのだけでも時間がかかりそうですが、ブルートフォースではこれを大量に計算するので計算量はもはや無限になってしまいます。
そこで賢く損失関数の最小値を求めてみよう、というのが微分を使った方法です。
この方法の名前が最急降下法 です。
2. 最急降下法
まず、単語の意味ですが、最急降下というのは、損失関数においてある点から損失を最も急に降下させる(方向)ということです。
つまり、パラメータで損失関数を微分することで損失を降下(小さく)する方向を逐次的に探してその方向にパラメータを調整させていく方法 のこと。英語でGradient Descentと言われ、勾配降下法とも言われます。
2.1 最急降下法の手順
- ニューラルネットワークに入力データを全部入れて予測値を出す。
- 正解値と予測値の二乗誤差である誤差関数を定義
- 誤差関数をパラメータで微分
- 微分して出た値でパラメータ更新
- 1.に戻る。(パラメータ更新の変化量がかなり小さければ終了。)
この手順を数式で表すと、下のような簡潔な式を繰り返すことと等しくなります。
$$
w_{t+1} = w_{t} - \alpha\nabla_w\mathcal{L}(w)
$$
ここで $w_t, \alpha, \nabla_w, \mathcal{L}(w)$ はそれぞれ、更新$t$回目のパラメータ、 学習率、 パラメータでの微分、損失関数です。パラメータを更新するための式は特に 更新式 と言われます。
2.2 最急降下法の更新式の意味
$$
w_{t+1} = w_{t} - \alpha\nabla_w\mathcal{L}(w)
$$
についてもう少し具体的に説明します。
データ(入力値と正解ラベル(値)のペア)が1000個あるとします。ニューラルネットワークは初めはランダムに $w_1$ と $w_2$ を持っています。
(手順1)その時のデータ1000個を使ってまずは予測値を1000個出します。(手順2)正解値との損失をMSEで定義します。ここで、手順3の微分に移る前に実際に1000個の損失を計算したとして、その1000個の損失の総和を全体の損失として図にプロットしてみましょう。
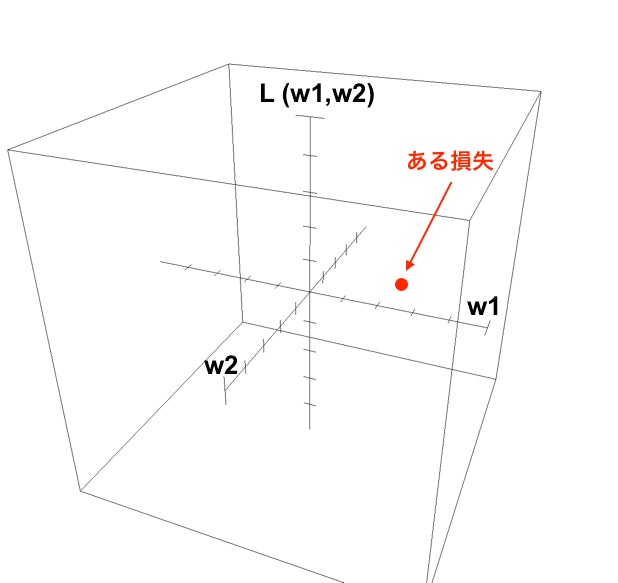
手順3からは現在の $w_1, w_2$ による損失よりも小さい損失となるように、 $w_1$ と $w_2$ を微調整します。その微調整には次の2点を決める必要があります。
- $w_1$ と $w_2$ をそれぞれ増やすかそれとも減らすか。
- それぞれどれだけ変化させるか。
先に結論を言うと、これらを解決する方法は
- 増やすか減らすかは微分 により求め、
- どれだけ変化させるかはあらかじめ私たちがなんとなく勝手に決めちゃう
のです。
私たちがなんとなく勝手に決めちゃうようなパラメータのことを ハイパーパラメータ と言い、他にハイパーパラメータの仲間として、「ニューラルネットワークの層の数」や「1層におけるニューロン(ユニット)の数」などがあります。
今回のどれだけ変化させるかを決定するハイパーパラメータのことを 学習率 と言います。
わかりやすさのため、上の2個のポイントをそれぞれ
- 微分
- 学習率
とします。
それでは最急降下法における、パラメータ値を増やすか減らすかを決めるプロセスを見ていきます。
2.2.1 [微分]増やすか減らすか
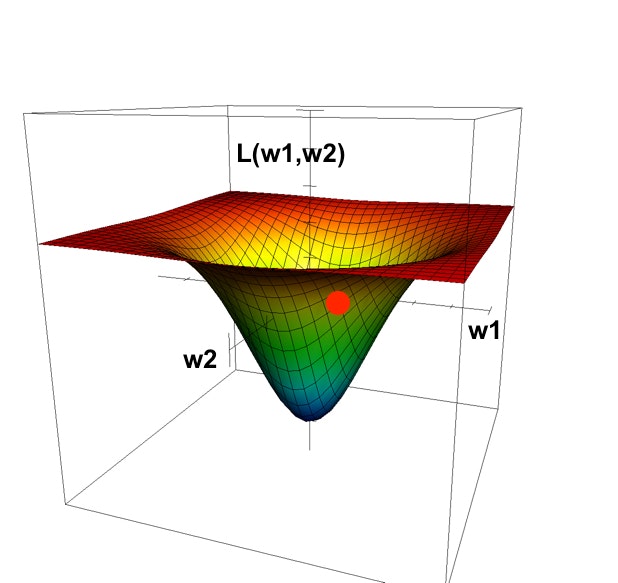
赤丸が現在のパラメータに対する損失を表しています。図のような位置に赤丸が損失関数に位置するときは $w_1$ と $w_2$ ともに小さくした方が良さそうです。
現在の損失(赤丸)が上のように位置するのであれば $w_1$ は大きくし、 $w_2$ は小さくした方が良さそうです。
あらかじめ上図のような全体を表すグラフが手に入らないのは前述した通りですが、最低でも今の $w_1$ と $w_2$ の位置がどういう傾きになっているかだけを見れれば $w_1$ と $w_2$ をどう変化させればいいかはわかりそうです。
ある点で傾きを取るといえば、まさに微分 ですね。
まずは $w_1$ で偏微分して現在の $w_1$ と $w_2$ を代入すれば $w_1$ 方向の傾きがわかり、
$w_2$ で偏微分して現在の $w_1$ と $w_2$ を代入すれば $w_2$ 方向の傾きがわかります。
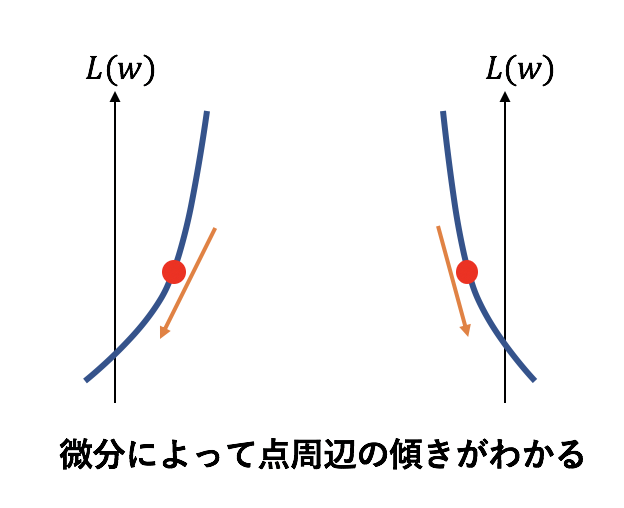
それによって、 $w_1$ と $w_2$ 近辺の傾きは上図のようにわかり、損失を下げるためには$w_1$ と $w_2$ を大きくするのかまたは小さくするのかがわかりますね。
2.2.2 [学習率]どれだけ変化させるか
といっても、あらかじめ決めておいた学習率(0~1の値)を使うだけ です。よく $10^{-5}$ や $10^{-2}$ などが見受けられます。この学習率を先ほど微分して出てきた値に掛けるだけ。
学習率は別名ステップサイズ(step size)とも呼ばれ、パラメータの1回の更新(ステップ)の大きさを表す値 になっています。
学習率が大きすぎるとステップが大きくなりすぎて最小値を通り越してしまい(=オーバーシュート)、逆に学習率が小さすぎると1回の更新で少ししか動かなくなり収束まで果てしない時間がかかってしまいます。
2.2.3 最急降下法の更新式のまとめ
データ全部を使ってその時の損失をプロットします。損失関数を今のパラメータ値で微分し、方向を求めます。出てきた方向に学習率をかけたら、その分だけパラメータ $w_1$ と $w_2$ を更新します。
更新した $w_1$ と $w_2$ をもつニューラルネットワークに再びデータ全部入れて損失を出しその結果からパラメータを更新する、というのを繰り返し、その更新量が任意のしきい値よりも小さくなったら学習が収束したものとして終わりです。
最後にもう一度更新式を見て見ましょう。第一項が現在のパラメータで第二項がそれを更新させる値です。ここで $\alpha$ が学習率、 $\nabla \mathcal{L}(w)$ がパラメータを更新する方向を表しています。
$$
w_{t+1} = w_{t} - \alpha\nabla_w\mathcal{L}(w)
$$
2.2.4 学習の収束について
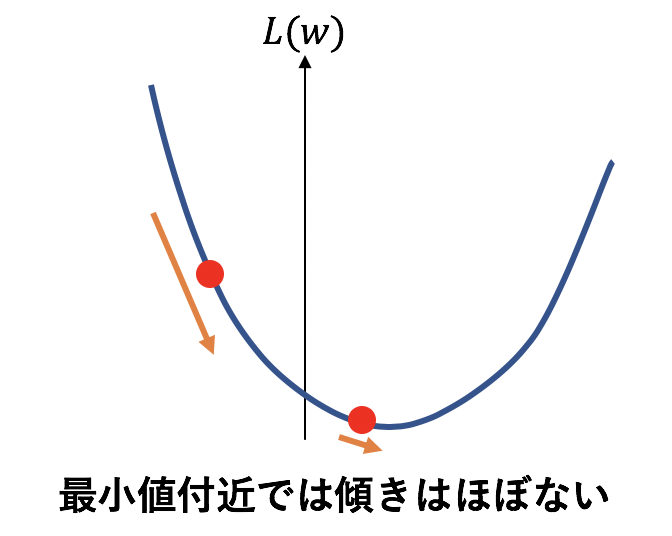
最小値から遠ければ勾配は大きくなるため、上式でパラメータへの更新は大きくなります。
一方で最小値付近傾きが小さいため勾配が小さくなります。つまり、パラメータの更新が小さくなります。最小値ではもはや傾きは0になりパラメータは全く更新されなくなります。
このように 最小値付近ではパラメータが全く更新されないため、パラメータの更新が小さければ学習終了、とみなせると言うことです。
2.3 最急降下法の欠点
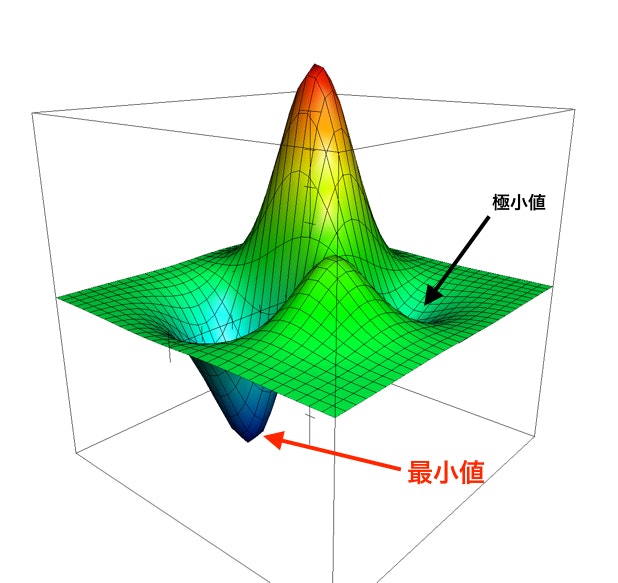
データ全部のことをバッチと言います。最急降下法では1回のパラメータ更新でデータ全部を使っているため、一気にパラメータを更新できますが、計算量が大きくかつ最適解ではない極小値に陥ってしまった場合抜け出せない、という欠点があります。ただ計算量が大きいことは、並列計算で解決できます。全データに対する勾配を計算しパラメータを更新するので、その全データに対する勾配の計算を複数のパソコンで並列計算すれば良いのです。それでは2つ目の極小値に陥った場合に抜け出せない、というのはどういうことでしょうか。例えば以下の図のような損失のときに
極小値で常に微分が0になってしまいます。これが極小値に陥ってしまうと言うことです。これを救ってくれるのがランダム性 です。
このランダム性を含んだ最急降下法こそが、SGD(=確率的勾配降下法)のこと です。
3. SGD
正式名称はStochastic Gradient Descentとよばれ、確率的勾配降下法と日本語ではよく言われます。
このSGDとはランダム性を含んだ勾配降下法のことと言いましたが、ランダム性をどう入れているのか。
それは至って簡単です。先ほどまでは一回のパラメータ更新に全データを使っていましたが、SGDは一回の更新ではデータを1つしか使いません。
最急降下法とSGDの違いは、パラメータの1回の更新に全データではなく、ランダムにピックアップした1つのデータを使うということだけ です。
これでSGDの説明は終わりなのですが、なぜこれで極小値に陥ることを解決してくれるのか、ということに少し触れます。
それは毎回ランダムに違うデータを使っているため、1つ前のデータでローカルに陥ったとしても次にランダムに選んだデータでは損失が大きくなる(または小さくなる可能性もあるが。)ため、再びパラメータが大きく更新され極小値から脱出できます。
毎回のパラメータ更新で同じデータを使っていると、一回極小値に陥ったら全く同じデータを入れているだけなので次もそこに陥り続け、結局抜け出せないのです。
3.1 SGDの欠点
1つのデータで勾配を計算し更新して、次のデータで勾配を計算し更新する、というのを逐次的に行うところに問題があります。つまり、1つのデータによる勾配で更新しないと次のデータには移れないということです。これは並列化ができません。
並列化ができるようにどうすればいいでしょうか。
次項のミニバッチ学習がこれを解決してくれるのです。
4. ミニバッチ学習SGD
全データを使ったバッチ学習ではまず全データの勾配を計算するのでその計算を並列化しました。一方でSGDは勾配計算のデータ数が1つでパラメータの更新が終わったら次のデータ1つに対してパラメータを更新しました。更新で使うデータ数が1つだからこそ並列化ができないのだから、このデータ数を増やせばバッチ学習のように並列化ができます。ただ、バッチ学習と同じように全データまで増やしてしまってはランダム性がなくなります。ということで、ミニバッチ学習SGDでは1回の更新で一定数のデータを使い学習 します。1回の更新で用いるデータ数は16個や32個などがよく使われ、このデータの塊を小さいバッチということでミニバッチ と言います。ミニバッチのサイズもハイパーパラメータです。マシンのスペックが高い場合は大きいサイズを指定できます。
4.1 ミニバッチ学習SGDの欠点
ここまでで最急降下法の欠点をある程度克服することができたのですが、
さらにはやく損失関数の最小値にたどり着きたいというモチベーションがあります。
そこで 学習を遅くしてしまう要因を考えます。その要因の1つとなっているのがPathological Curvatureにハマってしまうということ です。
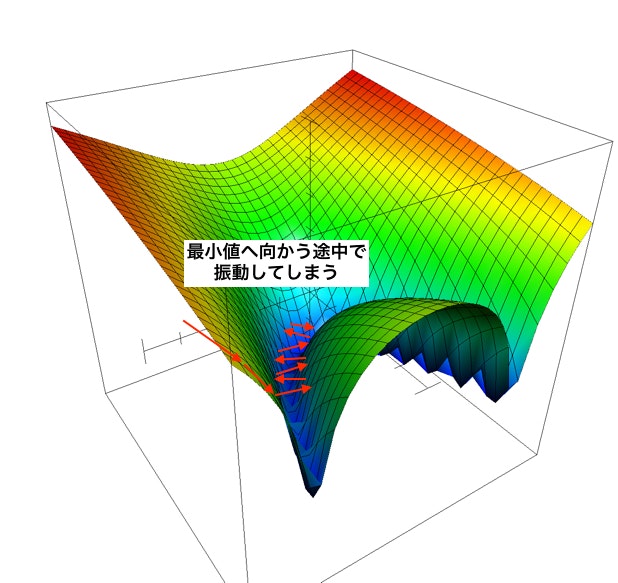
4.1.1 Pathological Curvatureとは?
Pathological Curvatureとは以下の図のような鋭いくぼみを持つ形状のことで、SGDだとオーバーシュート(1度の更新が大きすぎること)して振動を起こしてしまうため最小値にたどり着くのが遅いです。
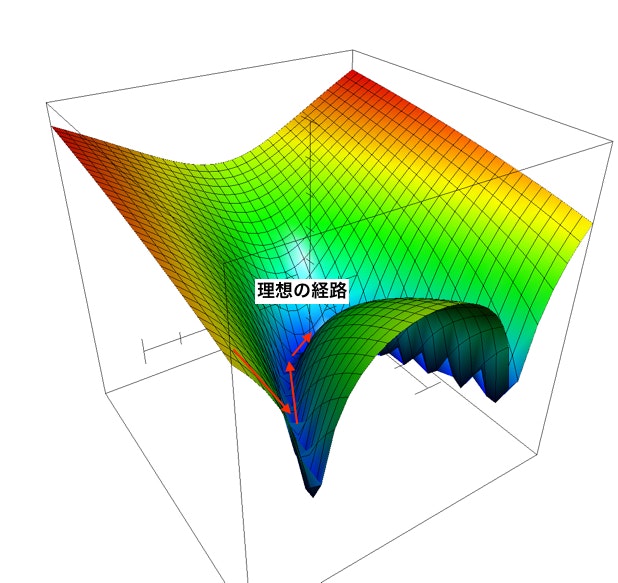
この振動を抑えて以下の図のようにさせることが理想です。
振動を抑えさせるものが、過去の勾配の変化を使う というものです。
代表的なものに モーメンタム と RMSProp があります。
ここでSGDの更新式をもう一度見て見ましょう。
実はここから説明する派生系ではこの式の第二項における モーメンタムは勾配(微分)を、RMSPropは学習率をいじっているだけ なのです。
このようにどちらもSGDに一工夫を加えているだけですのでここまで理解できていれば、ここからは難しいところは特にありません。ここからは微分をより正確に 勾配 と呼ぶことにします。ただ、これまでのように勾配は関数のある点での傾きの方向を表していると考えていて大丈夫です。
5. モーメンタム
モーメンタム(Momentum)は、損失関数上での今までの動きを考慮することでSGDの振動を抑える と言う考えで導入されました。
この モーメンタムは移動平均を理解すれば簡単に理解ができる のです。
5.1 移動平均とは?
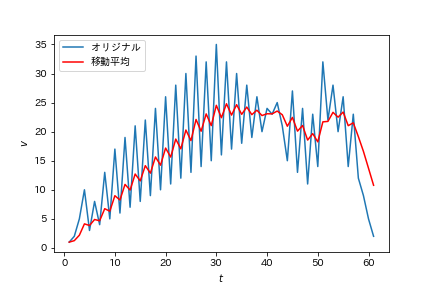
移動平均とは経済でよく使われ、急な変化があるグラフに対して移動平均を用いるとその変化がゆるやかになったグラフが得られる優れものです。(正確には指数平滑移動平均という仰々しい名前がついていますが、ここではわかりやすく移動平均に統一します。)
オリジナルの青線に対して移動平均を用いているのが赤線のグラフ。
振動を抑え、緩やかになっていることがわかります。
つまり、移動平均は急な変化に動じないグラフになっている ことがわかります。
この赤線は以下の式で各点を求め、プロットしています。
$$
\nu_t = \beta\nu_{t-1} + (1-\beta)G
$$
ここで $\nu_{t-1}, G$ はそれぞれ前時刻での移動平均された後の値、Gは現時刻の値で、$\beta$ は0から1の値を取るハイパーパラメータです。右辺において、
- 第1項 $\beta\nu_{t-1}$ : 今までの $G$ たちを蓄積した項
- 第2項 $(1-\beta)G$ : 現在の点を表す項
ということがわかります。$\beta$ が大きければ大きいほど第1項つまり今までの値の影響が大きく、第2項つまり現時刻の影響が小さくなります。
5.2 モーメンタムとは?
満を持してのモーメンタムの登場ですが、早速モーメンタムを使ったSGDの更新式を見せます。
\begin{align}
&\nu_t = \beta\nu_{t-1} + (1-\beta)\nabla_w\mathcal{L}(w) \\
&w_t = w_{t-1} - \alpha \nu_t
\end{align}
$\nu_{t-1}, \nabla_w\mathcal{L}(w), \alpha$ はそれぞれ前回の勾配、今の勾配、学習率です。$\beta$ は0から1の値を取るハイパーパラメータです。ここで $\nabla_w\mathcal{L}(w)$ を単純に $G$ と表してみます。
\begin{align}
&\nu_t = \beta\nu_{t-1} + (1-\beta)G \\
&w_t = w_{t-1} - \alpha \nu_t
\end{align}
SGDと異なり、式を2つ使っています。
まず第1式ですが、何か見たことありますね。
そうです、移動平均の式です。実はモーメンタムは単純に勾配を移動平均しているだけ なのです。
移動平均は急な変化に動じない、と言いましたがこれはつまり、振動のような急激に変化に動じない、ということですね。しかもPathological Curvatureで起きている振動は正負の符号が逆になるほどの振動ですね。前時刻で正の方向を向いていた勾配が現時刻では負の方向を向く勾配になってしまうほどの振動 です。この移動平均では前時刻と現時刻を足し合わせるので、正負で振動していると打ち消しあって振動が小さくなる のです。
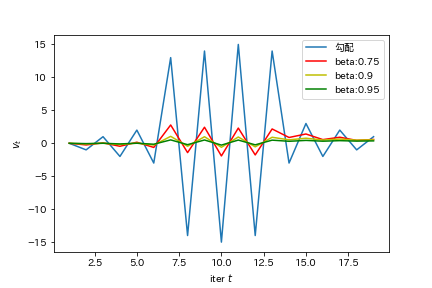
実際に正負が変わるほどの振動に対して移動平均(つまりモーメンタム)を適用すると、以下のグラフのようになります。
元々振動している勾配(青線)は大きくても見事に消失 されていますね。
第2式は移動平均後の値を使ってパラメータを更新しているだけです。とても簡単ですね。
5.3 モーメンタムを図で理解
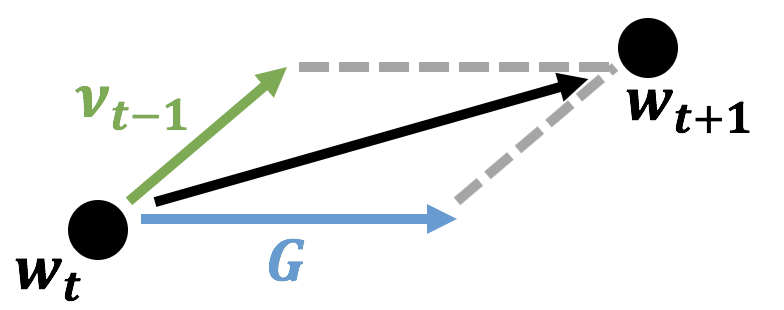
図(ベクトル図)を見ると、なぜモーメンタム(=慣性)と言われるのかが直感的にわかるかと思います。ここで上述の更新式をベクトル図で表すと、二項の和なので以下のように表せますね。
このように、現在の勾配の向きに対して、今まで動いていた方向つまり慣性(モーメンタム)の方向を足し合わせた方向を最終的な方向 としているのです。
5.4 モーメンタムの改良版 NAG
ここで モーメンタムの改良版と言われるNesterov(ネステロフ)の加速勾配法(=NAG) を紹介します。結論から言うと、Nesterovの加速勾配法はモーメンタムの更新式とほぼ変わりません。その説明の前にモーメンタムについてもう一度触れます。モーメンタムはずばり「過去の勾配たちを考慮することで急な変化を抑える」というものであり、動いているものはその方向に動き続けたいという慣性のようなものを現在の勾配に対して付け加えていました。この慣性こそがモーメンタムのことですが、そもそもこの慣性の方向が正しい方向(つまり損失を減らす方向)を向いているとは限りません。この慣性の方向が正しい方向であることを少しでも保証しようよ、というのがNesterovの加速勾配法 です。方向が正しいのかどうかの確認方法は今まで通り微分でできますね。ということで Nesterovの加速勾配法では、モーメンタム(慣性)だけで重みを更新した場合の勾配を先に見て、そのあと実際に慣性を加えて更新 します。これを式で表すと以下になります。
\begin{align}
&\nu_t = \beta\nu_{t-1} + (1-\beta)\nabla_w\mathcal{L}(w-\beta\nu_{t-1}) \\
&w_t = w_{t-1} - \alpha \nu_t
\end{align}
これをモーメンタムの更新式ともう一度比べて見ましょう。
\begin{align}
&\nu_t = \beta\nu_{t-1} + (1-\beta)\nabla_w\mathcal{L}(w) \\
&w_t = w_{t-1} - \alpha \nu_t
\end{align}
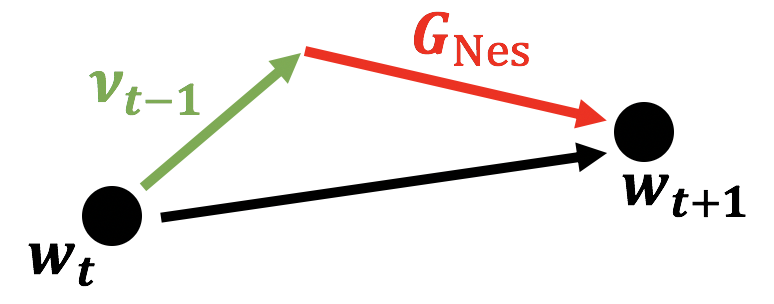
こう見ると違いが1つしかないことがわかりますね。先ほど述べたように 先に慣性項で重みを変更させてから勾配をとって更新 していますね。これをモーメンタム同様ベクトル図で書いてみると以下の図になります。
モーメンタムでは現時点から慣性および勾配を別々にとってから足し算をしていましたが、Nesterovでは先に慣性で重みを変更させてから勾配をとっていますね。
5.4.1 NAGに関する余談
ここからは余談というか私自身の理解の仕方なので正しいかは保証できない(私は正しいと思っているが。)のですが、NAGをもう少し噛み砕いた言葉で表すと、慣性項によって確実に損失が落ちる方向を先に見つけてから、実際にその点に向かわせる、のかなと思っています。上で表した図を段階をおって書くと、まず慣性項のみで重みを更新した場合に損失を小さくする勾配($w_{t+1}$)を先に見つけます。
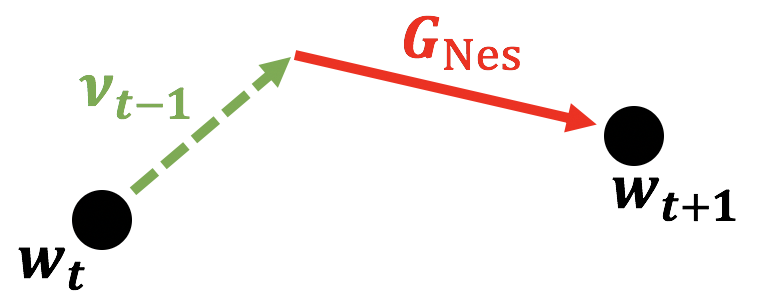
こうして $w_{t+1}$ を先に見つけます。$w_{t+1}$ は微分のおかげで確実に損失を下げるパラメータですので、あとはここに向かわせます。なのでそのためには点線の慣性項が必要ですね。つまり、Nesterovの加速勾配法の更新式第一式のように慣性項を足してあげます。ここでややこしくしているのは、慣性項を更新式の第一式内で2回も使っていてなんか慣性が効きすぎなんじゃないか、と思ってしまいそうになります。ただここで第一式で慣性項を追加しない場合、更新式のベクトル図は以下になってしまいます。
これでは所望の $w_{t+1}$ にたどり着けていない ですね。なのでちゃんと辿り着けるように慣性項を追加してあげて最終的には以下の図(再掲)のようになるのですね。
繰り返しになりますが、あくまでも私自身の理解では Nesterovの加速勾配法は慣性項によって損失が下がる方向を先に見つけてからその方向に向かわせる ものだと思っています。間違っていればご指摘いただけると大変助かります。Nesterovの加速勾配法に関してもっと詳細な説明はこちらの記事で解説されていましたので、そちらをご参照ください。
6. RMSProp
RMSPropはMomentumと同じくSGDの振動を抑えるという目的で作られたものです。ただこちらは 学習率を調整 しているのでした。
Pathological Curvatureでは振動方向は最小値方向に比べて勾配が大きくなっていますね。これを解決するには、振動方向の学習率を下げてあげれば振動を抑えられそうです。
RMSPropはgradの大きさに応じて学習率を調整する、というものです。
Momentumまで理解できていればとても単純なので早速更新式です。
\begin{align}
&\nu_t = \beta\nu_{t-1} + (1-\beta)G^2 \\
&w_t = w_{t-1} - \frac{\alpha}{\sqrt{\nu_t + \epsilon}} G
\end{align}
何か複雑そうに見えますが1式ずつみていくと実はとても単純なのです。 $\epsilon$ はゼロ除算を避けるための極めて小さい値($= 10^{-12}$ など)です。極めて小さいので計算結果には影響を及ぼしません。それ以外の記号の意味はモーメンタムのときと同じです。
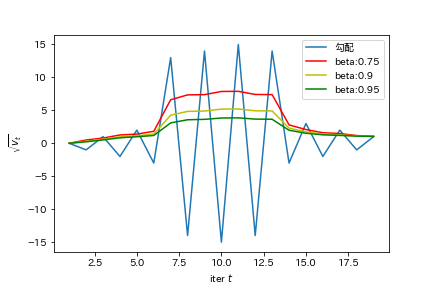
まず第1式は、移動平均の式です。 ここで注意して欲しいのは $G^2$ になっていること です。これにより、モーメンタムのように振動を正負で打ち消しあうのではなく、振動している時の値はかなり大きくなります。なんか良くなさそうですがこれが第2式に効いてくるのです。モーメンタムのように第1式をグラフで表します。
このグラフは元々の勾配(青色)に対するRMSPropの第1式の値たちです。勾配が急に変化するところでは第1式の値が大きくなっている ことがわかります。
第2式はパラメータを更新しています。ただし、ここでは元々の学習率を調整した上で更新しています。元々の学習率を第1式の値で割ってあげるだけです。振動しているときは第1式が大きくなるので、振動しているときの分母が大きくなり学習率を小さくしたい、と言う目的が達成できます。これにより振動が抑えられますね。
7. Adam
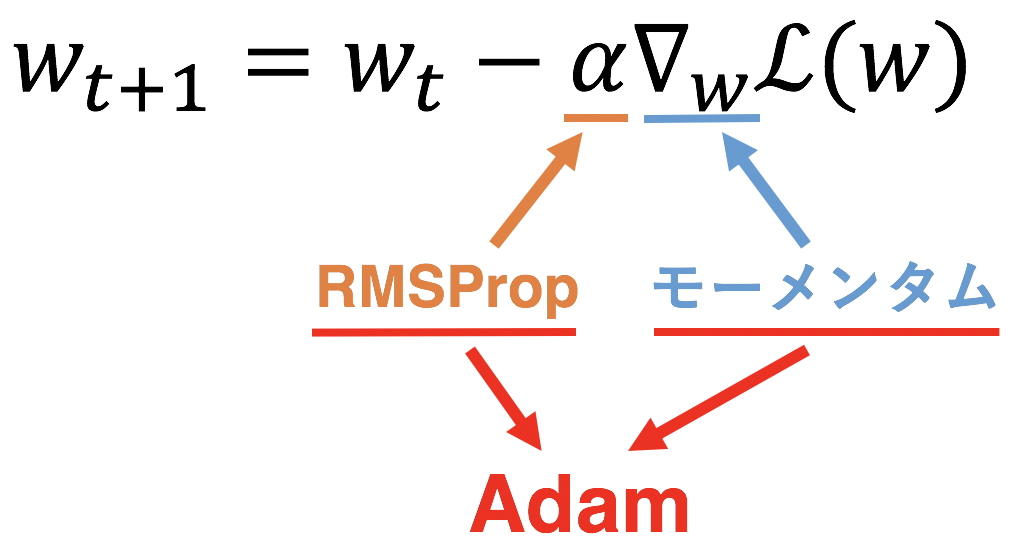
ライブラリなどでディープラーニングを実際に作ったことがある人なら何度も見たことがあるはずのAdam。ココに来てようやく登場です。Adamはいまやどのモデルにも広く使われているデファクトスタンダードな最適化アルゴリズムです。このAdamの正体はモーメンタムとRMSPropの良いどこどり というものです。移動平均で振動を抑制するモーメンタム と 学習率を調整して振動を抑制するRMSProp を組み合わせているだけなのです。早速更新式を見て見ましょう。
\begin{align}
&\nu_{t} = \beta_1\nu_{t-1} + (1-\beta_1)G \\
&s_{t} = \beta_2s_{t-1} + (1-\beta_2)G^2 \\
&w_t = w_{t-1} - \alpha\frac{\nu_{t}}{\sqrt{s_t + \epsilon}}
\end{align}
式が3つ出て来てしまいました。
ただ よくよく見るとAdamの正体がモーメンタムとRMSPropを組み合わせただけ、というのがわかると思います。
第1式と第2式はそれぞれ勾配の移動平均と勾配を二乗したものの移動平均になっており、ただのモーメンタム及びRMSPropの第1式です。
第3式はそれらを組み合わせて更新しているだけです。RMSPropの第2式にとても似ていますね。
それだけです。簡単にAdamを理解できてしまいましたね!
8. 【番外編】二階微分は使えないのか?
ここまでの最適化アルゴリズムは最急降下法ベースのものでした。
w_{t+1} = w_{t} - \alpha\nabla_w\mathcal{L}(w)
最急降下法というのは、損失関数を微分して損失が小さくなる方向に少しずつパラメータを更新するのでした。より正確に言えば、損失関数を1階微分して パラメータを更新します。今回紹介した最適化アルゴリズムは全て最急降下法を少し変更させたものであり、全て 1階微分を使った最適化アルゴリズム なのです。
ここで、1階微分ではなく2階微分まで使ったらどうでしょうか 。つまり、更新式が以下のような場合はどうなのでしょうか。
$$
w_{t+1} = w_{t} - \frac{\mathcal{L'}(w)}{\mathcal{L''}(w)}
$$
この2階微分を用いた更新式の手法をニュートン法(Newton's Method)と呼びます。詳細は別記事で解説しようと思っておりますが、ここではこのニュートン法の利点と欠点を簡単に紹介します。
利点
- ものすごい速さで学習が収束する。
- 2階微分まで考慮しているためより正確。
欠点
- 計算量が大きすぎる。最急降下法の計算量の2乗。
欠点が強すぎて実用はほぼされていません。
ただ使えるようになった暁には大きなブレイクスルーになるのでは、と思っています。膨大な計算量に対応できる量子コンピュータが完全に完成したらニュートン法を使えるようになるのかどうかとても気になります。
9. まとめと所感
まとめます。
- 最急降下法: 全データ を使って損失関数が最小値になるように、勾配を使ってパラメータ更新するよ。
- SGD: データ1つだけ をサンプルして使うことで、最急降下法にランダム性を入れたよ。
- ミニバッチSGD: データを16個とか32個 とか使うことで並列計算できるようにしたSGDだよ。
- モーメンタム: SGDに 移動平均 を適用して、振動を抑制したよ。
- NAG: モーメンタムで損失が落ちるように保証してあるよ。
- RMSProp: 勾配の大きさに応じて 学習率を調整 するようにして、振動を抑制したよ。
- Adam: モーメンタム + RMSProp だよ。今では至る所で使われているよ。
- ニュートン法: 二階微分 を使っているので、ものすごい速さで収束するよ。ただ計算量が膨大すぎて 実用されていない よ。
ニューラルネットワークを知るにあたって、最適化アルゴリズムの理解は避けて通れません。
ただ、ここまで読んだなら最適化アルゴリズムの気持ちをある程度理解できたかと思います。
理解してみると最適化アルゴリズムとは意外と単純なものでしたね!そしてニュートン法にはとてもロマンが溢れている感じがしました。今後はAdamの発展形やニュートン法などについてもさらに解説した記事が書ければと思っています。ここまでお読みいただきありがとうございました!
読んで少しでも何か学べたと思えたら 「いいね」 や 「コメント」 をもらえるとこれからの励みになります!よろしくお願いします!
Twitterで人工知能のことや他媒体で書いている記事などを紹介していますのでぜひフォロー@omiita_atiimoしてください!
10. 参考
-
Intro to Optimization in Deep Learning: Vanishing Gradients and Choosing the Right Activation Function
(英語) 物凄く参考にしています。勾配降下法からミニバッチ学習まで。 -
Intro to optimization in deep learning: Momentum, RMSProp and Adam
(英語) 物凄く参考にしています。上の続編。モーメンタムからAdamまで。 -
Stochastic Gradient Descent with momentum
(英語) モーメンタムについて図解でわかりやすく解説。 -
Exponentially Weighted Averages (C2W2L03)
Understanding Exponentially Weighted Averages (C2W2L04)
Gradient Descent With Momentum (C2W2L06)
(英語) Andrew Ng氏による移動平均とモーメンタムの解説動画。 -
Understanding Nesterov Momentum (NAG)
(英語) ネステロフの加速勾配法はモーメンタムの慣性項が正しい方向を向いているかを勾配によって確かめている。と書いてある。 -
最適化超入門
16枚目の最適化チートシートにそもそもの最適化問題の全体像がわかりやすくまとめられていて有能です。 -
機械学習をやる上で知っておきたい連続最適化
(Qiita) 連続最適化問題である最急降下法がどうやって求められており、その収束性などが反復法から始めわかりやすく解説されている。