本記事では、機械学習のタスクを解く上で非常によく登場する**最適化問題(optimization problem)**の基礎を解説していきます。
機械学習で用いる最適化といえば、SGDやMomentum、Adamなどが有名ですね。はじめ、それらに関しての解説を書こうかとも考えましたが、既に優れた記事が多々あるので、ここではほとんど触れません。
一方、最適化問題とは何か、アルゴリズムが"優れている"とはどう評価するか、などの最適化の基礎に関わる部分の情報が少なかったので、本記事ではそれらについて解説を行なっていきたいと思います。
最適化問題
まず、はじめに最適化問題の定義を与えます。最適化問題とは、与えられた条件のもとで何らかの関数を最小化(もしくは最大化)する問題のことを指します。
関数$f:R^n \rightarrow R$, $g_i:R^n \rightarrow R(i=1,...,m)$, $h_j:R^n \rightarrow R(j=1,...,l)$としたとき、最適化問題は次のようにあらわされます。
$$
\begin{array}{lrll}
& \min & \displaystyle f(x) & \\
& \rm{s.t.} & \displaystyle g_i(x) = 0 \ \ (i=1,...,m) \\
& &\displaystyle h_j(x) \leq 0 \ \ (j=1,...,l)
\end{array}
$$
ここで、$f(x)$を目的関数(objective function)、(機械学習の文脈ではロス関数(loss function)とも)、$g_i(x)$, $h_j(x)$を制約関数(constraint function)と呼びます。ここで、$g_i(x)$, $h_j(x)$はそれぞれ等式制約、不等式制約と呼ばれます。
このように制約条件の存在する問題を、**制約付き最適化問題(constrained optimization problem)と呼び、一方制約条件が存在しない問題、すなわち
$$
\begin{array}{rl}
\min & \displaystyle f(x)
\end{array}
$$
を無制約最適化問題(unconstrained optimization problem)**と呼びます。
最大化問題は考えなくて良いの?と思った方もいるかもしれません。最大化問題は、最小化問題の目的関数にマイナスを掛け、minをmaxへとすることで等価な問題として扱うことができるので、最適化の文脈では、しばしば最小化問題が中心として扱われます。
大域的最適解と局所的最適解
さて、最適化問題を解くためには、そもそも解とは何なのか、という定義を与えなければなりません。
最小化問題を考えると、一番小さい点が解になる、と直感的に考えられます。それを式であらわすと次のようになります。
任意の点$x \in R^n$に対して、
$$
f(x^*) \leq f(x)
$$
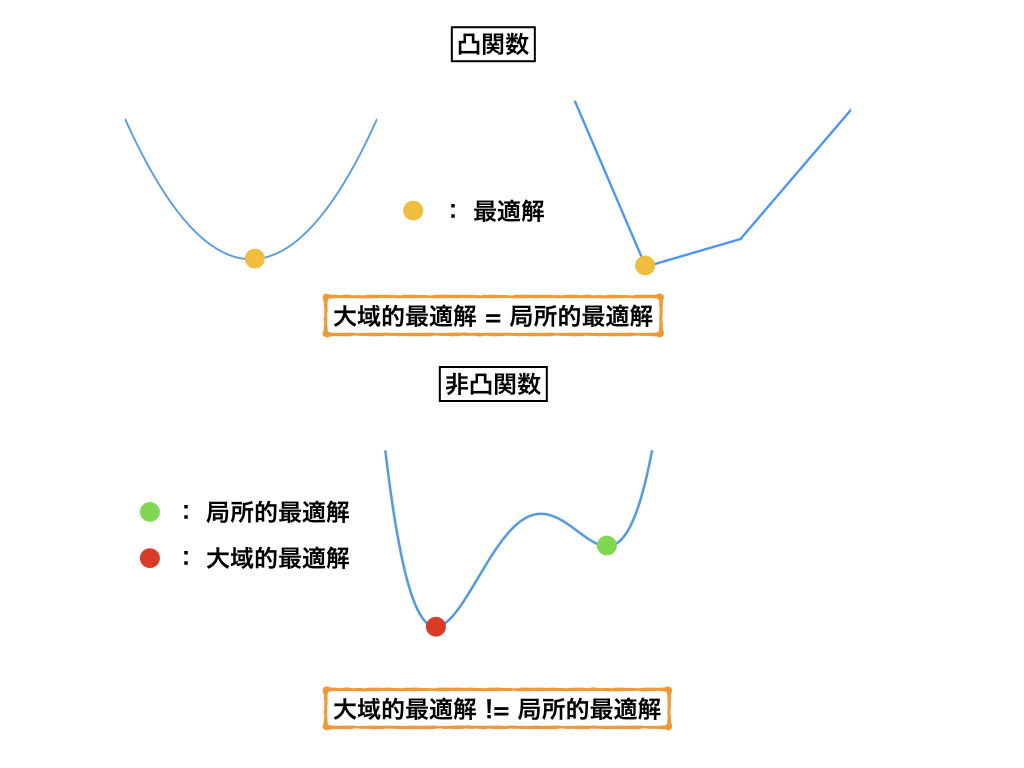
を満たす時、$x^*$を、**大域的最適解(global optimizer)**と呼びます。
これが、直感的な意味での関数値が"一番小さい"点ですね。しかし、最適化ではもう一つ重要な解の定義が存在します。それが、次の定義です。
$x^*$の$\epsilon$近傍の任意の点$x \in R^n$に対して、
$$
f(x^*) \leq f(x)
$$
を満たす時、$x^*$を、**局所的最適解(local optimizer)**と呼びます。
非常によく似た定義ですが、"近傍"の点と比較して、一番小さいという点が重要となります。図でみるとわかりやすいですね。
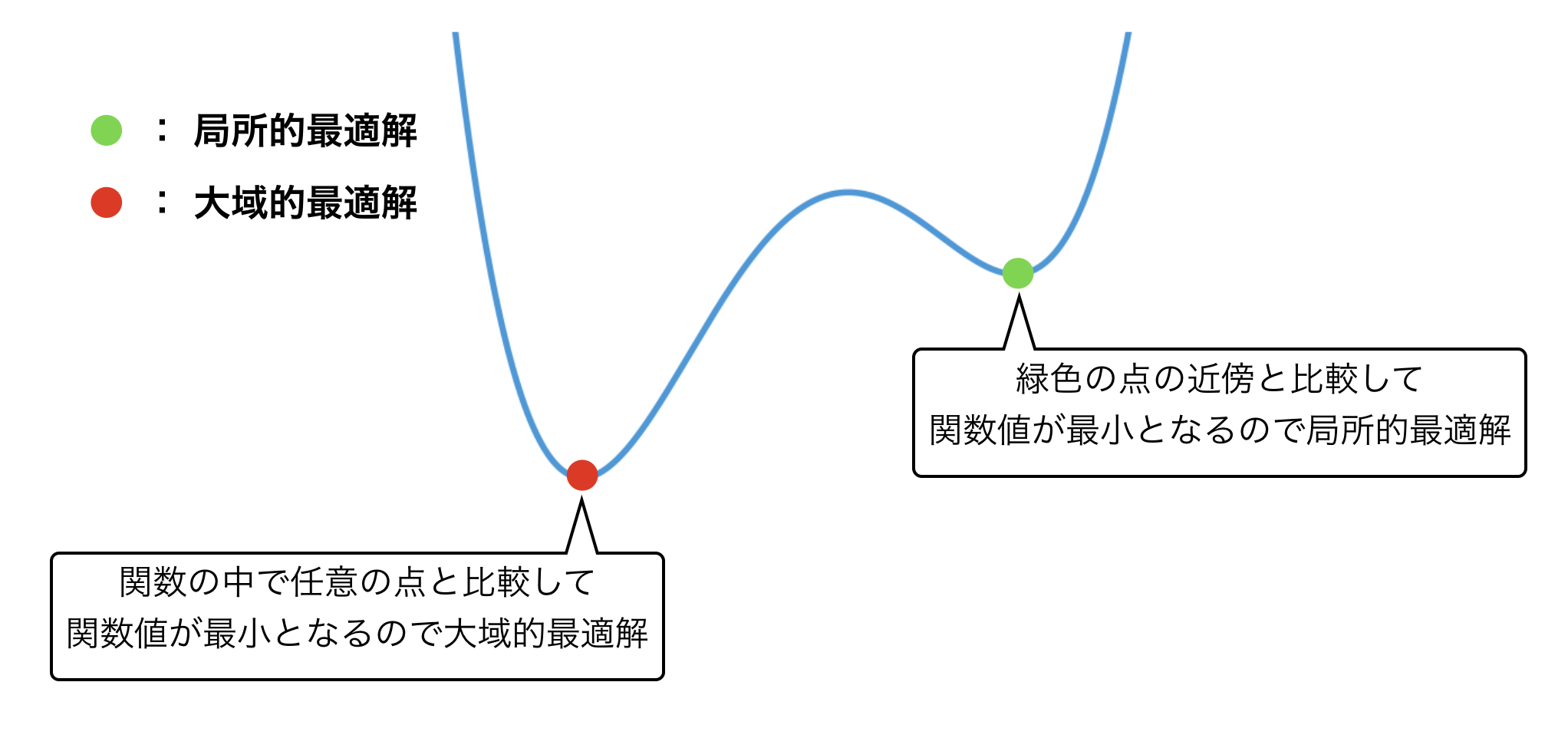
最適化問題を解く時、もちろん大域的最適解を求められれば良いのですが、初期点の位置や目的関数の性質によって、常に大域的最適解を求められるとは限りません。そこで、代わりに局所的な最適解を用いることがしばしばあります。
凸計画問題
最適化問題には、その問題の性質に応じて様々な分類が存在します。有名なところで言えば、目的関数と制約関数が線形関数である**線形計画問題(linear problem)**を聞いたことがあるかもしれません。
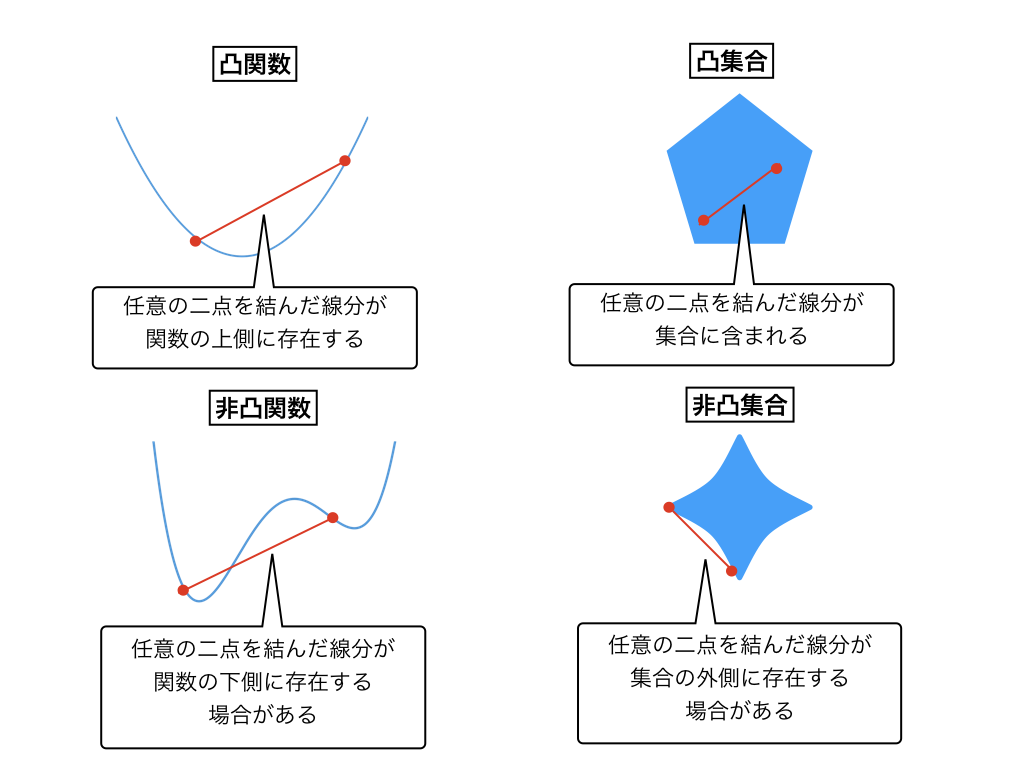
ここでは、非常に重要な概念である**凸計画問題(convex problem)**について紹介します。その準備のため、まず凸関数と凸集合の定義を与えます。
関数$f:R^n \rightarrow (-\infty, +\infty)$が任意の$x, y\in R^n$と$\alpha \in [0,1]$に対して、
$$
f((1-\alpha)x+\alpha y ) \leq (1-\alpha) f(x) +\alpha f(y)
$$
を満たすとき、$f$を**凸関数(convex function)**と呼びます。
これは、関数$f$の任意の二点を結んだ線分が常に関数の上に存在することをあらわします。
集合$S \subseteq R^n$において、
$$
x\in S, y\in S, \alpha \in [0,1] \Rightarrow (1-\alpha) x + \alpha y \in S
$$
が成り立つとき、$S$を**凸集合(convex set)**と呼びます。
これは、集合$S$内の任意の2点を結ぶ線分が$S$に含まれることを指します。
目的関数が凸関数であり、制約条件が凸集合であらわされるとき、その問題を**凸計画問題(convex problem)**と呼びます。
凸計画問題は、局所的最適解と大域的最適解が一致するという良い性質を持っています。また、さらに厳しい制約のもと、その解の一意性が保証される場合もあります。このような解析の容易さから、凸計画問題に対する多くの研究が行われてきました。
これに対し、非凸な問題は、一般に局所的最適解と大域的最適解が一致せず、解析は困難なものとなります。
凸関数の例
凸関数の簡単な例として、$f(x)=x^2$が挙げられます。
実際、
$$
(1-\alpha) x^2 +\alpha y^2 - ((1-\alpha)x+\alpha y )^2 = \alpha (1- \alpha) (x-y)^2 \geq 0
$$
より、凸関数であることがわかります。
ここでは、定義にあてはめて計算しましたが、関数が凸であるかは、その二回微分のヘッセ行列が半正定値であるかどうかを調べることで求めることができます。
$$
f^{''}(x) = \frac{d^2}{dx^2} x^2 = 2 \geq 0
$$
ここでは、簡単な関数を用いたので行なっていませんが、実際には、行列の固有値などから半正定値性を調べる必要があります。
反復法のアルゴリズム
ここからは、実際に最適解を求めるための反復法の説明を行います。
反復法は、適当な初期点$x^0 \in R^n$からスタートして点を次のように更新するようなアルゴリズムを指します。
$$
x^{k+1} = x^{k} + \alpha^k d^k
$$
ここで$d^k \in R^n$は、**探索方向(search direction)**と呼ばれ、この方向に進むことで$k$回目の反復点より、$k+1$回目の反復点の方が解に近づくことが期待されます。$\alpha^k$はスカラーで探索方向にどれぐらい進むかを制御するので、**ステップ幅(step size)**と呼ばれます。(機械学習の文脈では、**学習率(learning rate)**とも)
この更新を繰り返すことで、$x^k$が最適解$x^*$に十分近づいたとき、アルゴリズムを終了します。(理論的には、十分小さい$\epsilon$に対して$| x^k - x^* | \leq \epsilon$を満たしたとき、終了します。真の解がわからないから反復法を使っているのにどうやって判定するの?と思われた方はすごく良い勘をされています。実際の実装では、更新の幅が十分小さくなった時、終了する場合が多いです。)
点列の更新式から見てわかる通り、重要となるのはステップ幅と探索方向をどう決定するか、という点が挙げられます。
ステップ幅
ステップ幅の決め方は多々存在しますが、そもそもなぜ適切なステップ幅をとらなければならないのでしょうか。
それは、以下の図のような問題が生じるからです。

ここでは、最も基本的な決め方である**直線探索(line search)**を挙げます。
直線探索は、$d^k$に進んだときに、目的関数値を最小にする$\alpha > 0$をステップ幅とします。すなわち、
$$
f(x^k + \alpha^k d^k) = \min_{\alpha} {f(x_k + \alpha d^k)}
$$
を満たすものです。
ただし、直線探索は、複雑な関数となればなるほど正確なステップ幅を求めることが、計算量の点から難しくなり、実際には、固定のステップ幅($=0.1, 0.01$など)が用いられることも多いです。
理論的に良いとされているステップ幅の求め方として、Armijo条件、Wolf条件(後述)などが有名です。
一般には、序盤の更新で大きく解に近づいて、解の近傍では精度を良くするために小さく更新するようなステップ幅が良いとされます。
例えば、ステップ数(アルゴリズムの反復回数)を$k$として、
$$
\alpha^k = \frac{1}{\sqrt{k}}
$$
などとすると、反復が進むにつれて小さくなるようなステップ幅が得られます。
方向微係数
探索方向$d^k$の決定方法ですが、これは関数が減少する方向となることが期待されます。すなわち、
$$
f(x^{k+1}) - f(x^{k}) =f(x^{k} +\alpha ^k d^k) - f(x^{k})
$$
が負となるような$d^k$を求めたい、ということに他なりません。
ここで関数$f$が微分可能なとき、
$$
\lim_{t\rightarrow +0} \displaystyle \frac{f(x^{k} +t d^k) - f(x^{k})}{t} = \nabla f(x^k)^T d^k
$$
より、この右辺が負となれば良いことがわかります。(イメージしづらい方は、$f(x^{k} +\alpha ^k d^k)$をテイラー展開して、一次の項までで打ち切ってみてください。)
この右辺を、方向微係数と呼び、反復法ではこれが負となるような$d^k$を**降下方向(descent direction)**と呼びます。
連続最適化における様々なアルゴリズムは、この降下方向$d^k$の求め方が異なります。
最急降下法
最も基本的な降下法の一つである**最急降下法(steepest descent)**を紹介します。
まず、前小節より方向微係数は次のようにあらわされます。
$$
\nabla f(x^k)^T d^k = |\nabla f(x^k) |\ | d^k | \ {\rm cos} \gamma
$$
ただし、 $\gamma$は$\nabla f(x^k)$と$d^k$のなす角です。この式より、方向微係数を最小にするのは、${\rm cos} \gamma = -1$、すなわち$\gamma = \pi$のときであり、探索方向は
$$
d^k = -\nabla f(x^k)
$$
として、求められます。
このように、方向微係数を最小とする方向を用いて、解を探索するために最急降下法と呼ばれます。
アルゴリズムは、次の通りです。
- 初期点$x^0$を適当に定める。
- 現在の反復点$x^k$が終了条件を満たしていれば終了。そうでなければ3.へ。
- $d^k = -\nabla f(x^k)$を計算する。
- ステップ幅$\alpha^k$を計算する。
- 点を$x^{k+1} = x^k + \alpha^k (-\nabla f(x^k)) =x^k - \alpha^k \nabla f(x^k)$として更新する。
- 2.へ。
最急降下法の収束性
アルゴリズムを評価する上で、非常に重要な指標となるのが収束性、すなわち点列を更新して必ず解に辿り着くかどうか、という点です。
あまり収束性に触れることのなかった方は、アルゴリズムなんだから収束して当然では?と思う方もいるかもしれませんが、実際はアルゴリズムには収束する条件があります。
例えば、任意の初期点からはじめて収束するアルゴリズムなのかどうか、もしくは解の近傍を初期点としたときのみ収束するアルゴリズムなのか、大域的最適解に収束するのか、局所的最適解に収束するのか、などが異なります。
ここでは、最急降下法の収束性について見ていきます。
初期点を$x_0$とします。このとき、$f(x)$が下に有界、かつ集合{${ x\in R^n \ | \ f(x) \leq f(x_0) }$}で$f(x)$が連続的微分可能で、$\nabla f(x)$がリプシッツ連続であるとします。このとき、Armijo条件を満たすステップ幅を用いた最急降下法は大域的収束します。
簡単な証明を見ていきます。
点列の更新式
$$
x^{k+1} = x^k - \alpha^k \nabla f(x^k)
$$
から、点列{$x^k$}が収束するための、必要十分条件は$|| \nabla f(x^k) || \rightarrow 0(k\rightarrow \infty)$であることがわかります。
Zoutendijk条件より、仮定をおいたとき$x^{k+1}=x^k+\alpha^k d^k$で生成される点列{$x^k$}は、次の式を満たします。
$$
\sum_{k=0}^{\infty}\left( \frac{\nabla f(x^k)^T d^k}{||d^k||} \right) < \infty
$$
この式は、次のようにあらわされます。
$$
\sum_{k=0}^{\infty} ||\nabla f(x^k)|| {\rm cos} \theta_k < \infty
$$
ただし、${\rm cos} \theta_k$は
$$
{\rm cos} \theta_k = \left( \frac{- \nabla f(x^k)^T d^k}{||\nabla f(x^k)|| \ ||d^k||} \right)
$$
であらわされます。
ここで、最急降下法では、$d^k = -\nabla f(x^k)$なので、
$$
{\rm cos} \theta_k = \left( \frac{- \nabla f(x^k)^T (-\nabla f(x^k))}{||\nabla f(x^k)|| \ ||-\nabla f(x^k)||} \right) = 1
$$
が成り立ちます。よって、Zoutendijk条件より
$$
\sum_{k=0}^{\infty} ||\nabla f(x^k)|| < \infty
$$
が成立します。ここで、無限級数が収束するために、
$$
\lim_{k \rightarrow \infty} ||\nabla f(x^k)|| = 0
$$
が成立します。よって、アルゴリズムが進むにつれて、勾配のノルムが0に収束していくことがわかったので、大域的収束することがわかりました。(十分大きい$k$に対して、$||x^{k+1} -x^k|| \rightarrow 0$が成立)
最急降下法の収束率
アルゴリズムを評価する上で、収束性と並んで重要な概念が収束率です。これは、どのくらいの速さでアルゴリズムが収束するかをあらわします。
よく用いられる指標として、**q-1次収束(q-linear convergence)**が挙げられます。
これは、点列{$x^k$}が$x^{*}$に収束するとき、ある定数$c\in (0,1)$、整数$k'$に対して、
$$
||x^{k+1} -x^{*}|| \leq c||x^k - x^{*}|| \ \ (\forall k \geq k')
$$
が成り立つことを言います。すなわち、現在の反復点$x^k$と次の反復点$x^{k+1}$と解との差が線形に近くなることを示します。
さらに、
$$
||x^{k+1} -x^{*}|| \leq c||x^k - x^{*}||^2 \ \ (\forall k \geq k')
$$
が成り立つ時、**q-2次収束(q-quadratic convergence)**と呼びます。
体感的には、q-2次収束は非常に速く、10ステップ程度で収束するようなケースも多く、q-1次収束は数100ステップかかるようなイメージです。
最急降下法の収束率を見ていきます。
今、行列$A\in R^{n\times n}$が正定値対称で$b\in R^n$が定数ベクトルであるとき、問題
$$
\begin{array}{rl}
\min & \displaystyle f(x) = \frac{1}{2} x^TAx + b^Tx
\end{array}
$$
を考えます。
このとき、直線探索を用いて生成される点列{$x^k$}は、以下の式を満たします。
$$
||x^{k+1} - x^{*}|| \leq \left| \frac{\lambda - \mu}{\lambda +\mu} \right| ||x^k-x^{*}||
$$
ただし、$0<\lambda \leq \mu$はそれぞれ行列$A$の最小固有値、最大固有値をあらわします。
またノルムは$||v||=\sqrt{v^TAv}$であらわされます。
これより、最急降下法は1次収束することがわかりました。(証明は略)
SGD
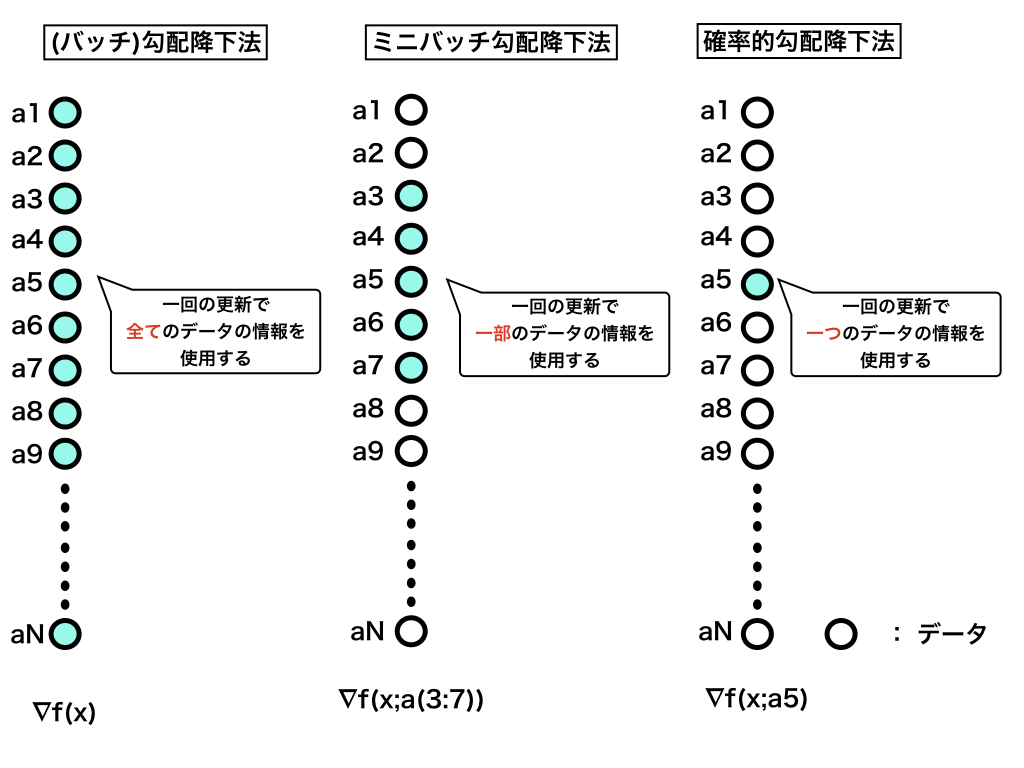
最急降下法では、一回の更新で全てのデータを見て点列を更新していました。しかし、データ数が膨大(100万~)となったとき、その全てのデータの情報を用いて、点列を更新するのは非常に計算量がかかります。
そこで、**確率的勾配降下法(stochastic gradient descent; SGD)**では、注目したデータに対してのみの更新を行い、これを繰り返すことで近似解を得ます。これにより、データ数が膨大な時でも、ある程度の精度の解を(通常の勾配降下法と比較して)高速に得ることができます。
さらに、一つずつではなく一定のかたまり(例えば100コずつ)のデータを用いて更新する方法を**ミニバッチ勾配降下法(minibatch gradient descent)**と呼びます。
まとめると以下のようになります。
最急降下法が理解できている方は、 SGDもすぐに理解できると思います。SGDは、収束することが証明されており、機械学習の文脈でもよく使用されます。ただし、収束率に関しては、データをどのような順番で学習するかなどに依存する部分もあり少し複雑になります。
その他のアルゴリズム
最急降下法は探索方向を$d^k = -\nabla f(x^k)$としていましたが、常にこれで良いのでしょうか。実際には、これでは上手くいかない場合(振動など)があります。そこで、より早く収束するような**共役勾配法(conjugate gradient method)**などが考えられています。
また、最急降下法では関数の一階微分までの情報しか用いていませんでしたが、より高精度な解を求めるため二回微分を用いて探索方向を決定する**ニュートン法(Newton method)などがあります。さらに、収束性を保証するため派生した、準ニュートン法(quasi-Newton method)、計算量を削減した記憶制限準ニュートン法(limited memory quasi-Newton method)**が知られています。
ただし、二回微分を用いた手法は非常に速い収束率を持つ一方、逆行列の計算などで計算量のオーダーが非常に大きくなるため、ビッグデータに対してはあまり向いていません。
機械学習では、冒頭に挙げた通り、慣性項を更新式に取り入れたMomentum、過去の勾配の減少情報を保持するAdamなどが有名です。
ただし、どのアルゴリズムも一長一短あり、問題との相性もあるので、一概にどれが優れているというのは言いづらいのが実際のところです。
おわりに
本記事では、最適化問題の基礎を取り上げてきました。
現在は、優れたライブラリが数多く揃っているので、問題の最適化を行う部分は数行書いて終わり、という方も多いと思います。
しかし、上手く収束しない時、ステップ幅をどのように変化させれば良いか、などを考える際には、最適化への理解が必要不可欠です。
本記事で、一人でも多くの方が最適化に興味を持って頂けると幸いです。
記事中の式、数値は実際計算を行いましたが、大きく間違っているなど、お気付きの点、またご感想がありましたら、遠慮なくコメントや@hiyoko9tの方へお声がけください。