オミータです。ツイッターで人工知能のことや他媒体で書いている記事など を紹介していますので、人工知能のことをもっと知りたい方などは気軽に@omiita_atiimoをフォローしてください!
他にも次のような記事を書いていますので興味があればぜひ!
画像認識に特化させた新たな活性化関数FReLU解説&実装!
今やあらゆる分野で驚くべき結果を残し続けているニューラルネットワークですが、そのニューラルネットに無くてはならないものこそが活性化関数です。ニューラルネットの非線形性を支えてくれている活性化関数ですが、今のデファクトスタンダードと言えばなんと言ってもReLUです。
シンプルかつ強力なReLUに打ち勝つ活性化関数として最近はSwish[Ramachandran, P.(2017)]やMish[Misra, D.(BMVC'20)]([拙著解説])などが提案されましたが、なんと最近画像認識に特化させた活性化関数が登場しECCV'20に採択されました。その名もFunnel Activation、通称FReLUです。画像認識に特化させているため、画像分類や物体検出、セマンティックセグメンテーションなどの分野でしっかりと性能向上を果たしている期待の新人です。それでは早速FReLUの仕組みとその凄さを見ていきましょう!
流れ:
- 忙しい方へ
- 論文解説
- まとめと所感
- 参考
原論文: "Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
公式実装: FunnelAct (MegEngine)
PyTorchでの再実装は下の「0.忙しい方へ」に記載。
0. 忙しい方へ
- FReLUは画像データの空間的依存性を考慮した画像認識特化型の活性化関数だよ
- 式で表すと単純だよ
$$
y=\mathrm{max}(x, \mathbb{T}(x))
$$
($\mathbb{T}(\cdot)$はただのDepthwise畳み込みだよ) - FReLUで画像分類/物体検出/セマンティックセグメンテーションで性能向上が確認できたよ
- 今まではReLUモデルに最適な手法やモデルなどが提案されてきたけど、これからはFReLUモデルに最適な手法を考えることでさらなる性能向上が期待できるよ
- 実装(PyTorch)で見ると簡単だよ
(筆者実装なのでミスなどがありましたらコメントしていただけるとありがたいです。)
import torch
import torch.nn as nn
class FReLU(nn.Module):
def __init__(self, in_c, k=3, s=1, p=1):
super().__init__()
self.f_cond = nn.Conv2d(in_c, in_c, kernel_size=k,stride=s, padding=p,groups=in_c)
self.bn = nn.BatchNorm2d(in_c)
def forward(self, x):
tx = self.bn(self.f_cond(x))
out = torch.max(x,tx)
return out
読んで少しでも何か学べたと思えたらTwitter@omiita_attimoもどうぞ!「いいね」 や 「コメント」もこれからの励みになります。よろしくお願いします!
1. 論文「Funnel Activation for Visual Recognition」解説
1.0 要約
早速ですが、今回紹介するFReLU(=Funnel Activation)はReLUやPReLUを2次元の活性化関数として拡張したものになっています。数式で表すととても単純で、
$$
y=\mathrm{max}(x, \mathbb{T}(x))
$$
となります。後ほど詳しく説明しますが、$\mathbb{T}(\cdot)$の部分が2次元空間での関数です。これにより、ピクセル毎の情報を捉えて複雑な見た目の画像にもしっかりと対応できるようになっています。
実験としてImageNet画像分類やCOCO物体検出、セマンティックセグメンテーションを行っておりそれぞれの画像認識タスクで性能を大きく向上しています。
公式実装はこちら(中国発DLフレームワークのMegEngineにて実装)にあります。
1.1 導入
CNNは画像認識分野では無くてはならないものとなっていますが、そんなCNNに特に大切なものとして畳み込み層と非線形活性化関数の2つがあります。
まず、畳み込み層にとって画像内の空間的な依存関係を掴むのは至難の技です。そのため、そういった局所的な依存関係を学ばせるために様々な正則化手法などが提案され精度向上を経てきました。ただし、それに伴い畳み込み層はますます複雑になっていき効率性を犠牲にしてきています。そこで、通常の畳み込み層だけで同じくらい高い精度を叩き出せないだろうか、という素朴な疑問が思いつきます。
続いてやってくるのが非線形な活性化関数です。線形的な関係を畳み込み層で学んだ後に、この活性化関数は通常スカラー値の変換を行います。代表的な活性化関数としてReLUが画像認識のみならず様々な分野で長い間使われています。ここで、画像認識に特化した活性化関数を作れないのだろうかという疑問が浮かんできます。
ここまでの2つの質問:
- 通常の畳み込み層での高い精度
- 画像特化の活性化関数
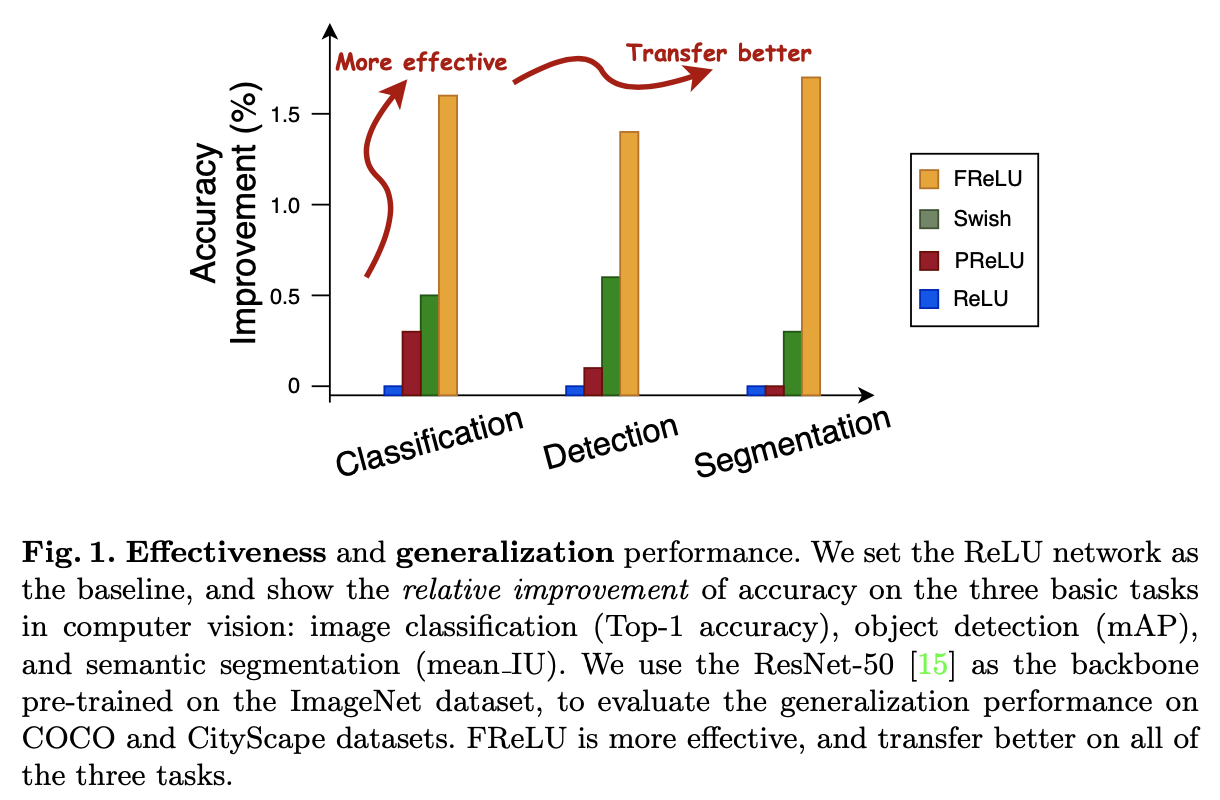
の両方に答えるべく提案されたものこそが今回のFReLUです。その結果、以下図のようにFReLUによる大幅な精度向上が確認できました。それぞれImageNetにおける画像分類、COCOにおける物体検出、CityScapeにおけるセマンティックセグメンテーションの結果で全てResNet-50を用いています。
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
FReLUは活性化関数のある問題を解決することでこのような結果を得られたわけですが、そのある問題というのは、活性化関数が空間的な要因を考慮しないという問題です。そこで、空間的な要因を考慮するためにReLUやPReLUを2次元空間に拡張させたものこそがFReLUです。式で表すと、
$$
y=\mathrm{max}(x, \mathbb{T}(x))
$$
で、$\mathbb{T}(\cdot)$は空間的要因を考慮する関数です。ReLUが$y=\mathrm{max}(x, 0)$で表されることを考えると、FReLUがReLUの拡張版であることはわかりますね。
1.2 関連研究
1.2.1 スカラー値の活性化関数
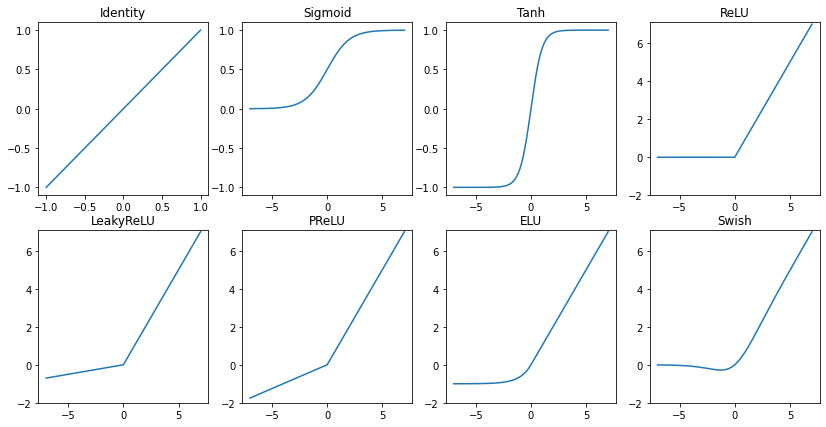
スカラー値の活性化関数とは単に、1つの入力値に対して1つの出力値を出す活性化関数のことで$y=f(x)$と表せます。みなさんが通常で使われている活性化関数はいずれもこれに該当するかと思います(少なくとも私はスカラー値の活性化関数以外は使ったことないです。スカラー値の活性化関数以外を通常で使う場面があればコメントかTwitterなどで教えていただけると嬉しいです)。ReLUがその代表例で、ReLUの負の部分を変更させたLeakyReLUやPReLU、ELUなども全て1つの入力に対して値を1つ返すのでスカラー値の活性化関数となります。ReLU一族以外のSigmoidやTanhなどももちろんスカラー値の活性化関数ですね。
1.2.2 文脈条件付き活性化関数
スカラー値の活性化関数が1つのニューロンにのみ依存するのに対して、文脈条件付き活性化関数(= contextual conditional activation)は多対1の関数です。つまり複数のニューロンたちに依存した関数となっています。代表的なものがMaxout[Goodfellow, I.(2013)]と呼ばれるもので、式は$\mathrm{max}(w_1^Tx+b_1, w_2^Tx+b_2)$と表されます。この式からもMaxoutは複数のニューロン(というか層)に依存したものとなっていることがわかる。ただしこの手法は計算量が増えすぎています。
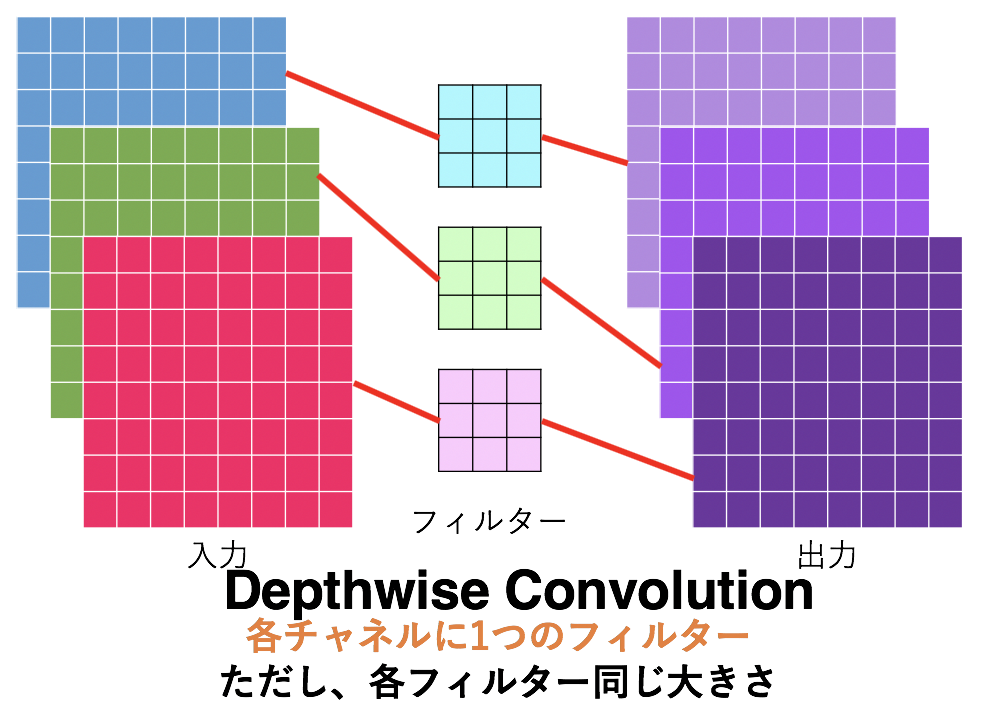
FReLUではMobileNet系でよく使われるDepthwise畳み込みを用いることで、計算量を抑えたまま空間的依存性を考慮した文脈条件付き活性化関数を実現しています。
Depthwise畳み込みは単に入力の各チャネルに1つのフィルターがある畳み込み層で、パラメータ数が大幅に削減できるのでモバイル系のCNNモデルによく使われる畳み込みです。より詳しく知りたい方は拙著の「パラメータ数を激減させる新しい畳み込み「MixConv」解説!」または「MobileNet(v1,v2,v3)を簡単に解説してみた」を参照してください。ちなみにPyTorchではConv2dのgroups引数をチャネル数と同じにすることでDepthwise畳み込みを実現できます。
in_c=64
torch.nn.Conv2d(in_channels=in_c, out_channels=in_c, kenel_size=3, groups=in_c)
1.2.3 空間的依存性を考慮したモデル
空間的依存性を学習させることは難しく、効率性を犠牲にしたDilated畳み込み(a.k.a Atrous畳み込み)などが提案されてきました。Dilated畳み込み層とはその名の通り通常の畳み込みを膨張したような畳み込みとなっており、以下図がその例を表しています。PyTorchでもnn.Conv2dにdilation引数が用意されており、デフォルトではdilation=1に設定されています。(以下図はdilation=2の例。)
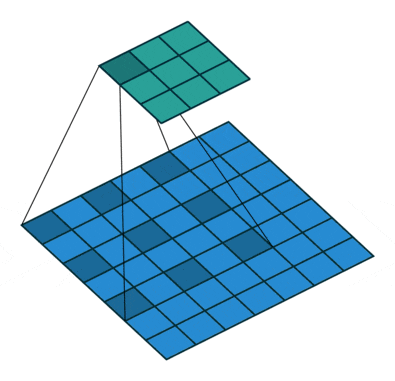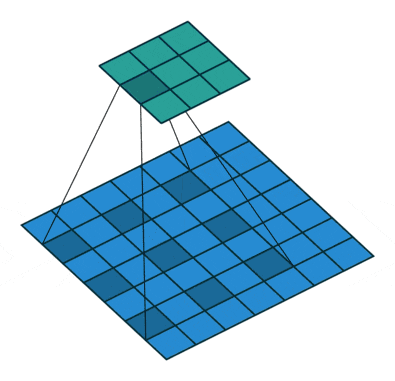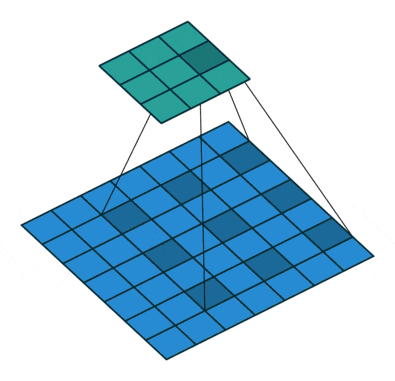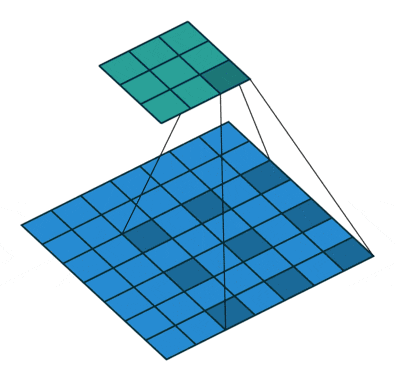
"A guide to convolution arithmetic for deep learning", Dumoulin, V., Visin, F. (2016)
他にも空間依存性を学習させるようなSTN[Jaderberg, M.(NeurIPS'15)]やGCNet[Cao, Y.(ICCVW'19)]などもありますが、いずれも効率性を犠牲にしてしまっています。こういった複雑な手法よりも単純なFReLUが優っているというから驚きです。
1.2.4 受容野
画像認識において、受容野(=Receptive field)の場所とサイズはとても重要な役割を果たしており、結果への貢献度は各ピクセルごとに異なることや中心部分のピクセルの影響力が大きいことなどは研究によってわかっています。そのため、畳み込みに対して複雑な機構やAttentionなどを組み込むことで最適な受容野を学習させる試みは多く行われてきました。
本論文ではFReLUというシンプルでかつ効率的な手法で最適な受容野が学習されるようにしています。FReLUは受容野を非線形な活性化関数の中に取り組むことで、結果として複雑な畳み込みたちよりも高い性能を示しています。
1.3 Funnel Activation
ここからはいよいよ画像認識特化型の活性化関数であるFReLUの説明に入っていきます。FReLUの特徴といえばなんと言っても空間的要素を考慮した2次元のFunnel Conditionを使っているということです。さらにFReLUによってピクセル毎のモデリングも可能にしています。Funnel Conditionなどについてここから詳しく説明していきますが、まずはReLUとPReLUの復習から入っていきましょう。
1.3.1 ReLUとPReLU
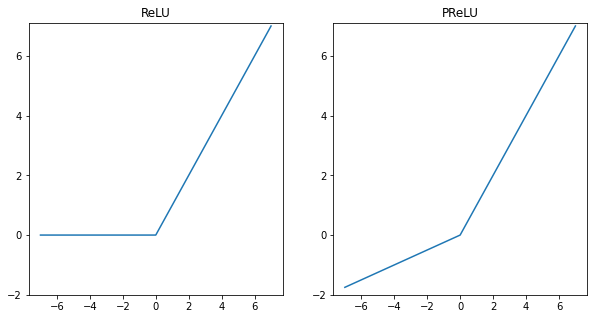
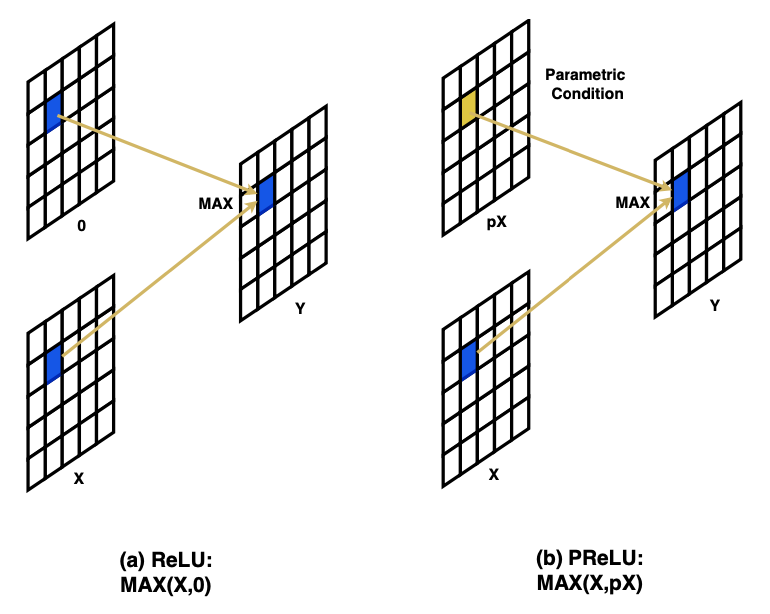
まず左図のReLUですが、式は$\mathrm{max}(x,0)$です。その特徴として
- 非線形として$\mathrm{max}(\cdot)$を使っていること
- 条件に用いた$0$という値は人間が定めたものであること
というものがあります。
そしてこの発展形として、右図のPReLUがあります。式は$\mathrm{max}(x,0)+p\cdot\mathrm{min}(x,0)$となります。PReLUは、ReLUの負の部分の傾きをゼロにするのではなく学習可能なパラメータ$p$で決定するようにしたものです(初期値$p=0.25$)。ここでパラメータ$p$は畳み込み層の各チャネルそれぞれに独立して存在します。
ここで$p<1$という条件では、このPReLUは$\mathrm{max}(x,px)$と書き換えられます。この変形をもう少し丁寧に説明します。$p<1$という条件で$\mathrm{max}(x,px)$を見ると、$x$が正なら$x>px$で$x$のまま出力されますし、$x$が負なら$px>x$で$px$がしっかりと出力されていますね。なので$p<1$においては変形は妥当そうです。ここで、パラメータ$p$は各チャネルごとに存在しPReLUは各チャネルに$p$を掛け算します。各チャネルごとの畳み込み操作であるDepthwise畳み込みを思い出せば、PReLUは1x1 Depthwise畳み込みと解釈することもできます。ReLUとPReLUをそれぞれニューラルネットっぽく図示すると以下図のようになります。
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
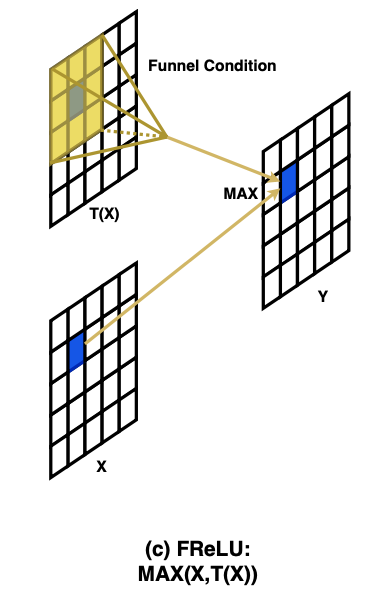
1.3.2 Funnel Condition
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
FReLUはReLU一族同様$\mathrm{max}(\cdot)$を採用しています。FReLUでは2次元空間を考慮した条件となっており、上図がその図になっています。上図からもわかるように2次元空間の関数$T(\cdot)$とはただの畳み込み演算のことです。理科の実験で使う漏斗みたいな形をしているので、漏斗=Funnelという名前がついていそうですね。
それではFReLUを数式で見てみましょう。FReLU$f(\cdot)$は次の式で定義されます。:
$$
f(x_{c,i,j})=\mathrm{max}(x_{c,i,j}, \mathbb{T}(x_{c,i,j})) \
\mathbb{T}(x_{c,i,j})=x^\omega_{c,i,j}\cdot p^\omega_c
$$
ただし、
$$
x^\omega_{c,i,j}\cdot p^\omega_c=\sum_{i-1\leq h \leq i+1, j-1\leq w \leq j+1}x_{c,h,w}\cdot p_{c,h,w}
$$
ここで、$x_{c,i,j}$は画像の$c$番目チャネルの位置$(i,j)$のこと。そして$\mathbb{T}(\cdot)$は2次元空間の関数で、Funnel Conditionと呼ばれています。Funnel Conditionの式で$x^\omega_{c,i,j}$はパラメトリックプーリングウィンドウ(Parametric Pooling Window)と呼ばれ、$x_{c,i,j}$を中心とした$k_h\times k_w$のウィンドウです。ウィンドウサイズはデフォルトで3x3です。$p_c^\omega$はその係数を表しています。$p_c^\omega$はチャネルごとに異なります。(PReLUと同じですね。)
つまり、このFunnel ConditionはただのDepthwise畳み込みであることがわかります。
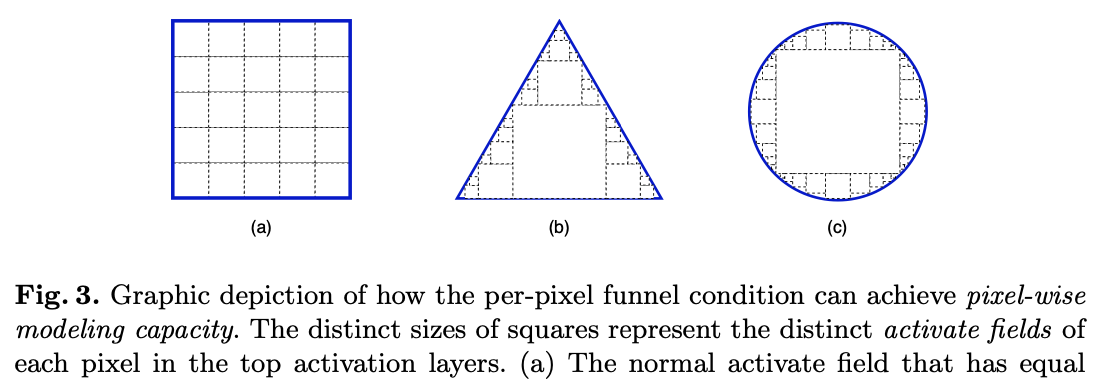
1.3.3 ピクセル毎のモデリング
上で定義したFunnel Conditionによって、各ピクセルに対して空間的な要素を考慮した条件(つまり$\mathbb{T}(\cdot)$)を学習できるようになりました。これはつまり、各ピクセルにおいて空間的な要素を取り込む($\mathbb{T}(x_{c,i,j})$)かそれともそのピクセルのままにするか($x_{c,i,j}$)を$\mathrm{max}(\cdot)$によって判定させることができる、ということです。これにより、これまではどのピクセルにおいてもそのままの形でしか取り込めなかった情報も、Funnel Conditionによってあるピクセルでは空間的な要素を取り込みまた別のピクセルでは特に取り込まずにそのままであるか選択できるようになるため、下図のようにいろいろな形に対応することができます。画像内に写っているオブジェクトが矩形型であることのほうが珍しいので、このような特性は画像認識分野において非常に役立ちそうなことがわかります。
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
1.3.4 実装について
FReLUは、単にDepthwise畳み込みによる値と元の値を各ピクセルにおいて$\mathrm{max}(\cdot)$で選択させているだけです。初期値には正規分布の値を用い、パラメータ数もDepthwise畳み込みを入れているだけなのであまり大きくはありません。実装の際にはバッチノームも続けて入れており、PyTorchによる実装は次のようになります。ものすごく単純です。あとはお好みで初期値の設定などをしてください。
class FReLU(nn.Module):
def __init__(self, in_c, k=3, s=1, p=1):
super().__init__()
self.f_cond = nn.Conv2d(in_c, in_c, kernel_size=k,stride=s, padding=p,groups=in_c)
self.bn = nn.BatchNorm2d(in_c)
def forward(self, x):
tx = self.bn(self.f_cond(x))
out = torch.max(x,tx)
return out
1.4 実験
1.4.1 画像分類
1.4.1.1 実験条件
まず、画像分類タスクでその性能を見てみます。データセットには、訓練データ数128万枚、評価データ数5万枚を有するImageNetを用います。モデルには様々なサイズのResNetと軽量モデルであるMobileNet/ShuffleNetを用いています。この時、最終ブロック以外の全てのReLUをFReLUなどに置き換えて比較実験を行います。活性化関数としてReLUとFReLU以外にPReLUとSwishも用いて比較しています。その他実験条件については下表にまとめました。モデル評価は評価用データセットのTop-1精度で行っています。
| パラメータ | バッチサイズ | ステップ数 | 学習率 | 学習率スケジューラ | 重み減衰率 | ドロップアウト率 |
|---|---|---|---|---|---|---|
| 値 | 256 | 60万 | 0.1 | 線形スケジューラ | 1e-4 | 0.1 |
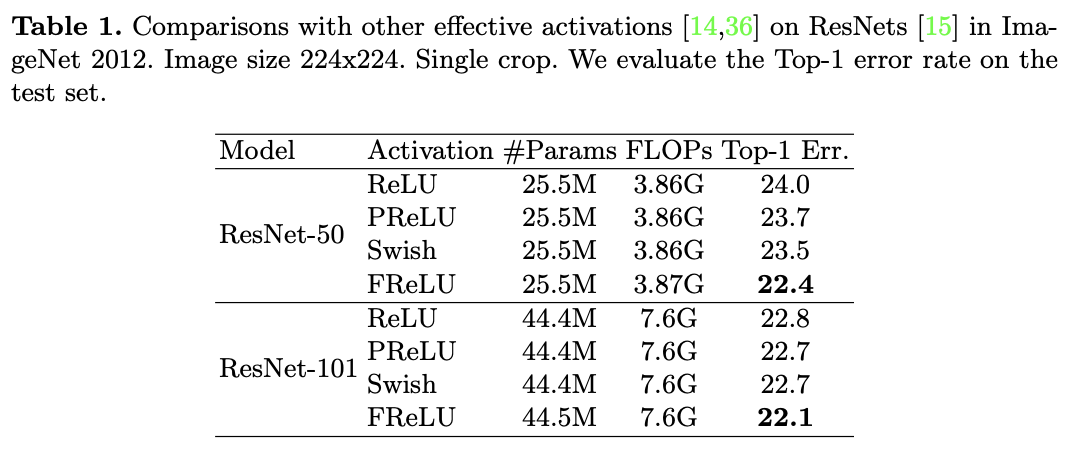
1.4.1.2 ResNetによる比較
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
上表がResNet-50/-101の結果です。エラー率なので低い方が性能が高いです。FReLUが一番いいですね。ベースラインのReLUと比べると、FReLUはResNet-50/-101のそれぞれで1.6%/0.7%のゲインがあります。また、FReLUのパラメータ数とFLOPsを見ると計算量的にも問題がないことがわかります。すごいですね。
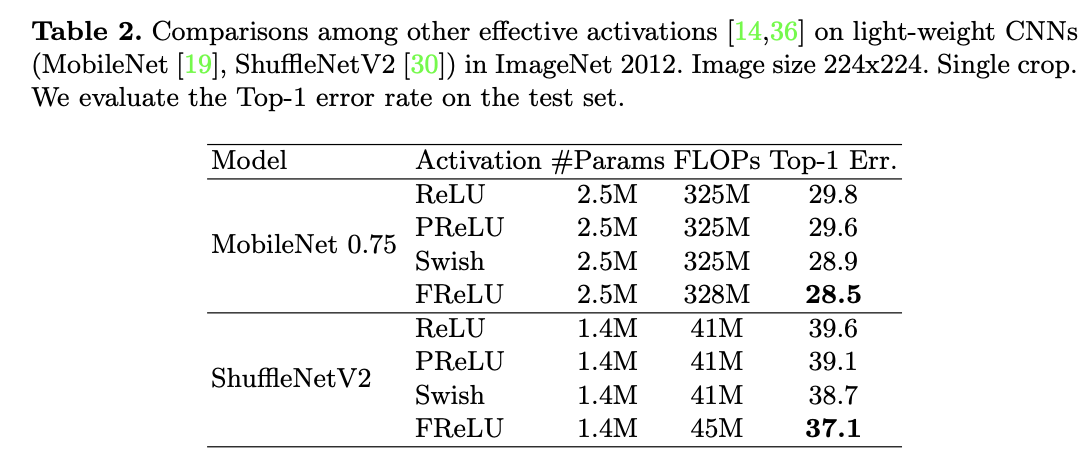
1.4.1.3 軽量モデルによる比較
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
続いて軽量モデルでもその効果を見てみましょう。ここではMobileNet0.75(通常のMobileNetよりも幅(=チャネル数)が少ないモデル)とShuffleNetV2を用いています。上表の結果を見てみるとまたしてもFReLUが一番低いエラー率を叩き出していますね。ShuffleNetV2においてはReLUと比べて2.5%もゲインがあります。
ここでもパラメータ数/FLOPsはあまり問題ではないことがわかります。
1.4.2 物体検出
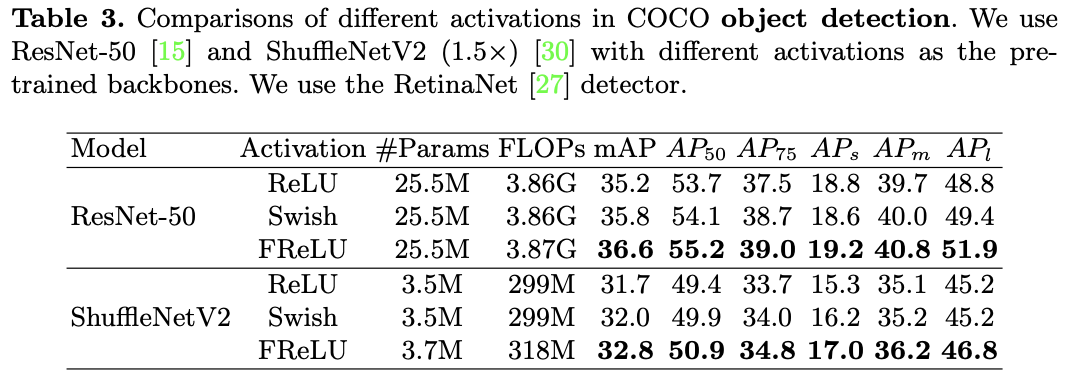
画像分類タスクでは性能向上がしっかりと確認できました。そうなると続いては物体検出です。80個のクラスを持つCOCOデータセットを用います。モデルはRetinaNetを用い、バッチサイズは2です。バックボーンモデルとしては1.4.1の画像分類タスクで学習させたモデルたちを用いています。
上表が実験結果です。特にResNet-50をバックボーンとして用いた際には、FReLUがReLU/Swishに対してmAPでそれぞれ1.4%/0.8%ほどまさっていることがわかります。それ以外にも$AP_s, AP_m, AP_l$を見ると、FReLUが小/中/大サイズの物体いずれにおいても性能向上を果たしていることがわかります。軽量モデルであるShuffleNetV2においても同様に性能向上ができていますね。
1.4.3 セマンティックセグメンテーション
画像分類、物体検出と来たら続いてはセマンティックセグメンテーションです。データセットは19個の
クラスを有するCityScapeを用いています。モデルはPSPNetで、8個のGPUそれぞれにバッチサイズ2として計算を行っています。バックボーンに1.4.1で学習させたResNet-50を使用しています。
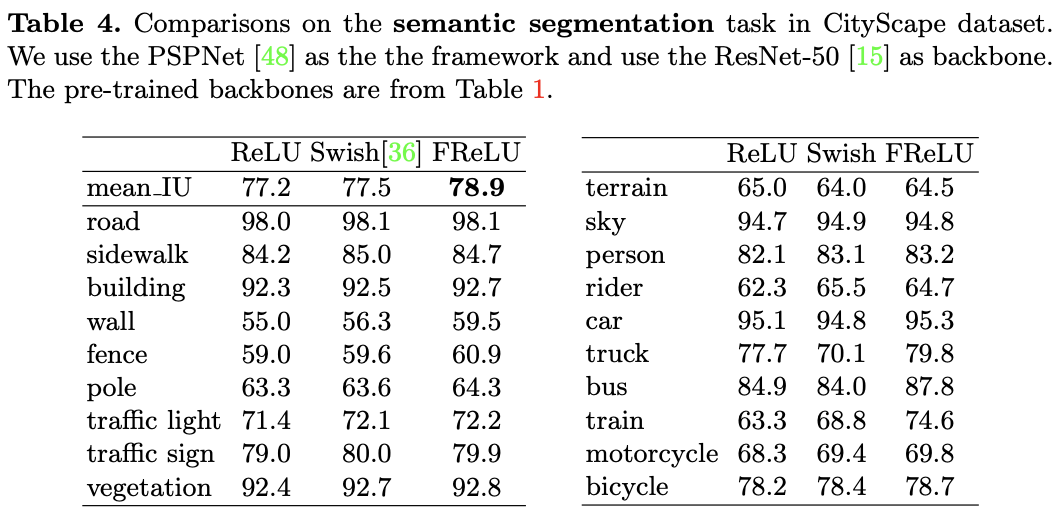
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
結果は上表で、FReLUがmean_IUでベストな性能となっています。また、クラスごとに見てみると'train'/'bus'/'wall'などで大きく性能が向上していることがわかります。
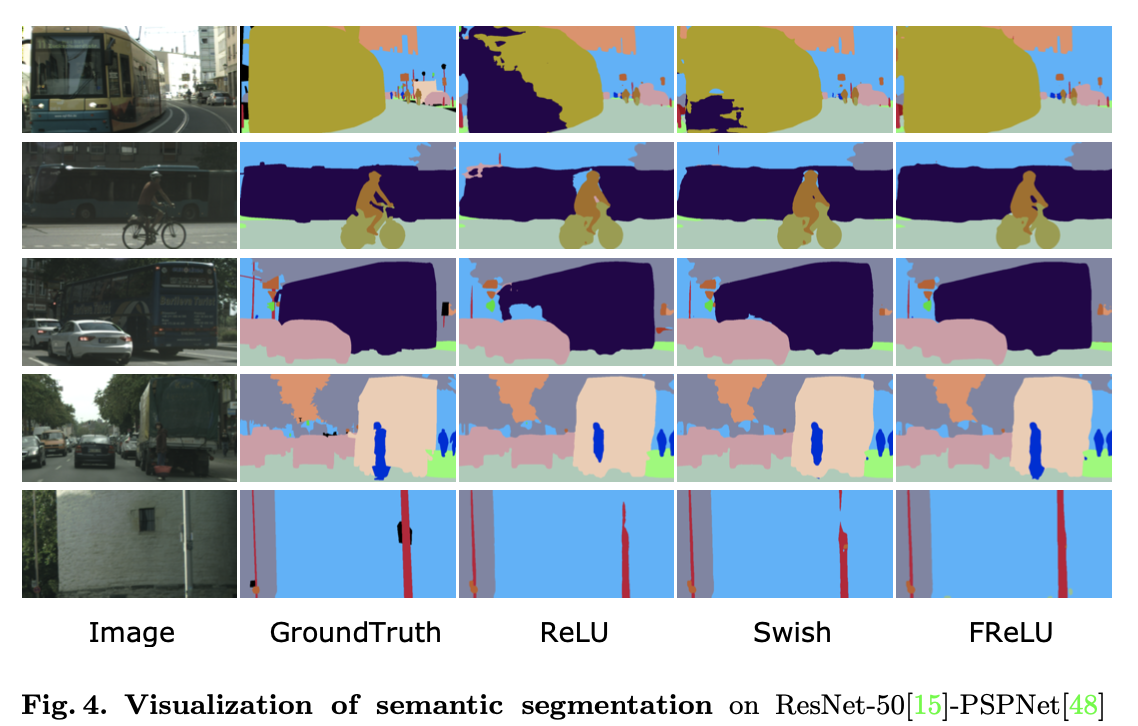
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
上図を見ると、ただ単に活性化関数をFReLUに変えるだけでより良い色塗りができていることが視覚的にもわかりますね。これは1.3.3でも述べたように、FReLUがピクセル毎に最適な範囲を指定できるため物体の複雑な形にも対応ができると考えられますね。
1.5 考察
ここからはアブレーションスタディとして次の2点について考えていきます。
- FReLUの特性
- 他の既存手法とのFReLUの相性
1.5.1 FReLUの特性
FReLUは、
- Funnel Condition
- 非線形関数$\mathrm{max}(\cdot)$
の2つの部品で構成されています。ここではその2つそれぞれの効果について考えていきます。
1.5.1.1 Funnel Condition
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
まず、FReLUでは空間的な依存性を獲得するためにFunnel Condition(つまりDepthwise畳み込み)を用いていますが、そもそもパラメータは必要なのでしょうか。ここでは、Funnel Conditionの代わりに最大プーリング/平均プーリングを用いてみます。モデルはResNet-50で上表がImageNetの結果です。明らかにパラメータを含むFunnel Conditionが一番いいですね。(パラメータがない場合は2%も性能が劣化しています。)
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
ちなみに、実装でもFunnel Condition直後にバッチノームを入れていますが、ここを他のレイヤーノーム/インスタンスノーム/グループノーム(バッチノーム一族についての簡単な説明はこちらで解説)を入れた場合はどうなのかについても実験した結果がした表です。モデルはShuffleNetV2でここでもImageNetの画像分類です。レイヤーノームとグループノームがベストな結果となっていますが、それならこの論文ではなぜバッチノームを一貫して使ってきたのか。その理由を筆者に聞いたところ、推論時間がバッチノームの方が早いためということでした。
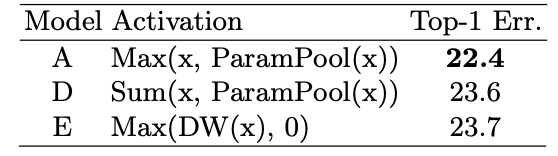
1.5.1.2 非線形関数max
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
FReLUでは非線形関数として$\mathrm{max}(\cdot)$を利用しています。この$\mathrm{max}(\cdot)$関数に先ほどのFunnel Conditionを組み込むことで空間的な依存性も同時に獲得しています。これと比較するものとして、非線形な$\mathrm{max}(\cdot)$の代わりに線形な$\mathrm{sum}(\cdot)$を使った場合と単に$\mathrm{DW}(\cdot)$(=Depthwise Convolution)を使った場合の2つを用いています。上表がその結果です。
ここで、ParamPool自体がDepthwise畳み込みであるにもかかわらず、DWというものが登場してきて混乱したので筆者に確認したところ、ParamPoolとDWは同じものであるそうなので、Eは$\mathrm{Max}(\mathrm{ParamPool}(x), 0)$とも書けます(そしてEはさらに$\mathrm{ReLU}(\mathrm{ParamPool}(x))$とも書けますね)。FReLU(A)が一番いいですね。
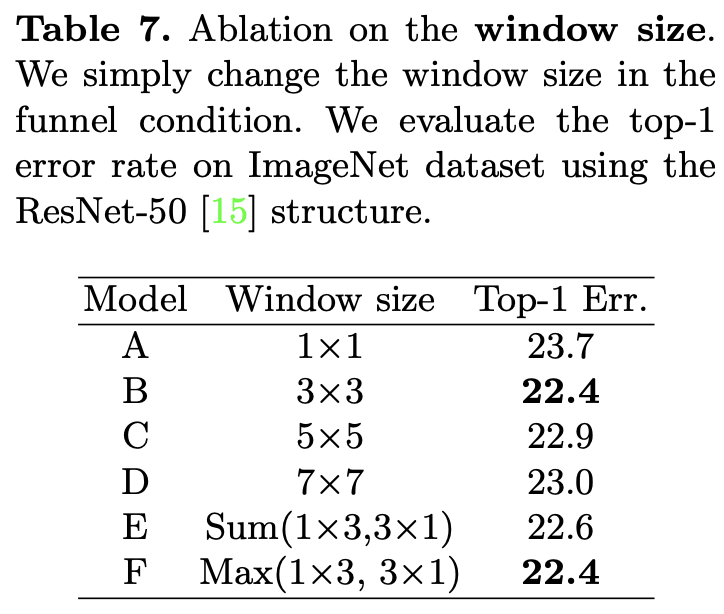
1.5.3 ウィンドウサイズ
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
デフォルトではウィンドウサイズを${3\times3}$としていますが、${1\times1, 3\times3, 5\times5, 7\times7}$のそれぞれで実験を行っています(上表A-D)。また、EとFではウィンドウの形を正方形ではなく、$1\times3$と$3\times1$を同時に使った場合でも実験を行っています。この時それぞれのウィンドウで畳み込んだ結果を1つにまとめるときにSumかMaxを使う場合でも比較実験をしています。
上表から特筆すべきは次の2つです。
- 3x3が一番良いこと
- 正方形ではないフィルタでもベストな結果(F)が出ていること
特に2つ目に関しては、ウィンドウが正方形でないが故に1.3.3で説明した様に多様な形状の物体を捉えることができるからと考えられます。
1.5.2 他の既存手法とのFReLUの相性
FReLUを実際に使うにあたって問題となるのが、果たしてどの層にFReLUをぶち込むべきかということです。さらにSENetなどの既存の手法に対しても相性がいいのかも調べます。
1.5.2.1 どの層にFReLUをぶち込むべきか
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
まずはどの層の後にFReLUを入れるべきかということですが、ここでは「1x1Convの直後」、「3x3Convの直後」、「両方」のパターンで実験を行っております。ここで「3x3Convの直後はまだわかるけど、いきなり1x1Conv?」と思った方が居るかもしれませんが、これはResNet-50はBottleneckモジュール内で、MobileNetはDepthwise Separable Convolutionにて1x1Convをしっかりと使っていますので、そこのことを言っています。Depthwise Separable Conv.などについてはこちらで解説しましたのでそちらもご参照ください。上表の結果を見ると、1x1Convおよび3x3Convのそれぞれの直後にFReLUをぶち込むのがベストであることがわかります。
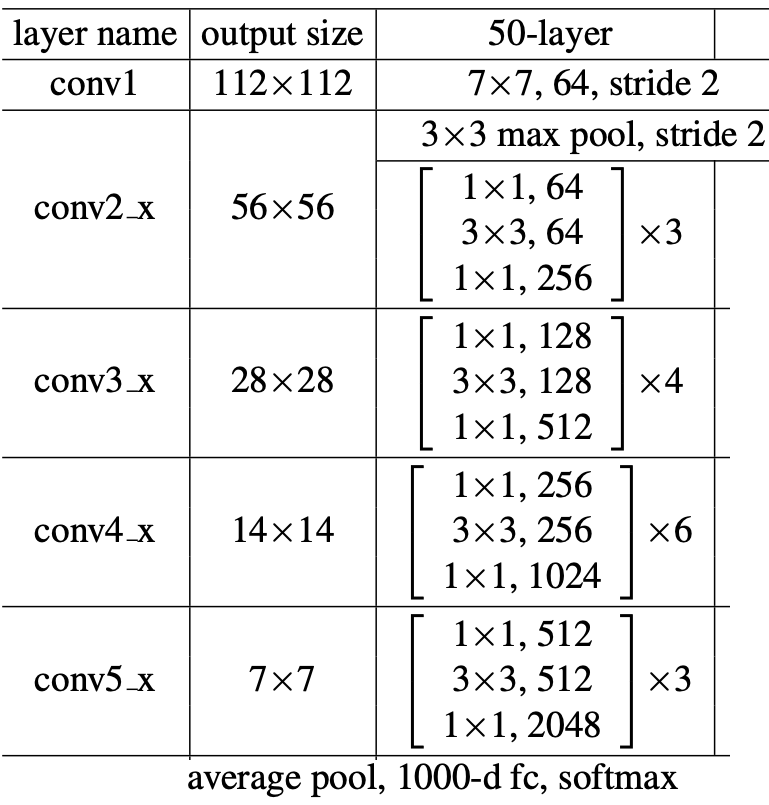
"Deep Residual Learning for Image Recognition", He, K.(2015)(改変)
またさらに、ResNet-50においてどのステージにFReLUを入れるのがベストなのかについても調べています。この論文で言うステージとは上のResNet-50のアーキテクチャの'layer_name'に対応してます。conv1がステージ1でconv2_xがステージ2という具合です。結果は以下表です。ステージ5は画像サイズが7x7と小さいためここでは考慮していません。結果は下表です。
全ステージ(2-4)にFReLUを入れるのがベストであることがわかりますね。また、ステージ2/3単体のゲインが大きいことからも浅い層(=画像サイズが大きい層)でFReLUが効果を発揮することがわかります。
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
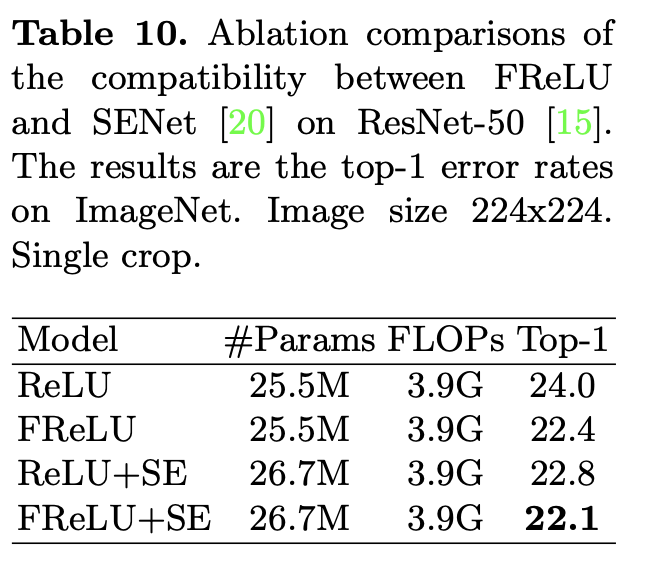
1.5.2.2 SEモジュールとの相性
SENet[Hu, J.(CVPR'18)]で使われているSEモジュールとFReLUを組み合わせた場合にさらなる性能向上が見られるかを実験しています。そもそもSEモジュールとは何か簡単に言うと、どのチャネルが大事なのかをAttentionで決定するモジュールのことで詳しくはこちらで解説しましたのでご覧ください。非常に単純な割に強力なモジュールです。
"Funnel Activation for Visual Recognition", Ma, N., Zhang, X., Sun, J. (ECCV'20)
そんなSEモジュールとの相性ですが、実験的にはFReLUと相性が良いことがわかりました。上表がその結果です。FReLU+SEがベストであることもさることながら、FReLU単体でReLU+SEよりも優れた性能を示していることがもっと驚きです。このことからFReLUは他の既存手法とも良い相性を示す可能性がありますね。
1.6 結論
本論文では、画像認識特化型の活性化関数FReLUを提案しました。シンプルかつ効果的で他の手法とも相性が良いFReLUは、画像認識分野の新たな活性化関数として期待ができます。他の手法と組み合わせることでさらなる性能向上も望まれます。
2. 所感とまとめ
ReLUに打ち勝つためにSwishやMish[拙著解説]などが提案されてきましたが、このFReLUは画像認識に特化させた活性化関数ということでとても面白く感じました。実際に画像認識タスクでReLUとSwishを打ち負かしており、実装も簡単なのでこれからが期待ができる活性化関数です。画像認識モデルであれば、今使っている活性化関数をFReLUに総入れ替えして使ってみてはいかがでしょうか。
Twitterで人工知能のことや他媒体で書いている記事などを紹介していますのでぜひフォロー@omiita_atiimoしてください!
こちらもどうぞ: