【GIF】初心者のためのCNNからバッチノーマライゼーションとその仲間たちまでの解説

CNNからバッチノーマライゼーションとその仲間たちまでを図で解説！

ディープラーニングが流行するきっかけとなった分野は画像認識と言っても過言ではないでしょう。
実際にディープラーニング流行の火付け役となった2012年のAlexNetは画像分類タスクにディープラーニングを適用させて驚異的な結果を出しました。AlexNetの論文は現時点(2019年12月現在)で 被引用数 52,655を誇るバケモノ論文 になっています。このAlexNet以降で 画像認識分野で使われている技術こそがCNN(Convolutional Neural Network) なのです。(もちろん最強の画像認識モデルEfficientNet(拙著の解説記事)もCNNベースです。)

このCNNの層を深くしていくことで精度を向上させていくのですが、
層を深くすればするほどCNNが逆にうまく学習してくれなくなってしまうのです。
それを解決した技術がバッチノーマライゼーション(Batch Normalization) (以下、バッチノーム)です。(ちなみにこの論文の被引用数は2019年12月現在で14,761でこちらもバケモノ論文。)このバッチノームは今では当たり前のように使われています。バッチノームの仲間である レイヤーノーマライゼーションというのはTransformer(拙著の解説記事)でも使われており、バッチノーム系はディープラーニングにとって必要不可欠な技術 になっています。

本稿では CNNの解説から入り、バッチノームおよびその仲間たちを徹底解説 します。本記事は以下の構成です。

1. CNNってそもそもどう動いているの？
2. バッチノーマライゼーションとは？
3. バッチノーマライゼーションの仲間たち
4. (オプション)なんでバッチノーマライゼーションって強いの？
5. まとめ
6. 参考

読んで少しでも何か学べたと思えたら 「いいね」 や 「コメント」 をもらえるとこれからの励みになります！よろしくお願いします！
(間違いなどもございましたら、ご指摘よろしくお願いします。)

1. CNNってそもそもどう動いているの？

まずCNNがどう動いているかについて解説します。
わかりやすさのため、以下では全て入力が白黒(グレースケール)の画像だとします。
カラー(RGB)の場合は入力画像がカラーに変わるだけで他は何も変わらないので、
グレースケールさえ理解できれば大丈夫です。

1.1 入力画像1枚、フィルター1枚のCNN

まずは入力画像が1枚、フィルター1枚の時を考えましょう。
左から右へと流れていく感じです。

入力画像にフィルター(カーネルとも言われる。)がかかり、フィルター後の画像に対して活性化関数を適用することで出力の画像が得られます。これで畳み込み層(Convolution層)が出来上がります。
フィルターをかけるプロセスを見てみます。

入力画像の3x3の部分がフィルターによって1マスになります。この フィルターをかける処理こそが「畳み込み」と言われる処理 です。
そうして 出来上がった画像は一回り小さくなっているので、パディング(padding)と言われる処理を施す ことで元の画像サイズと同じにします。パディングは出力された画像の周りに任意の数字を埋めていく処理で、0で埋めることが多いです。(zero padding)

このフィルターによって得られた画像は、例えば、「元の画像よりカドの明暗がはっきりしている画像」だったり、「元の画像より境界線がはっきりしている画像」のように、画像の基本的な特徴が浮き出ている画像となっています。このフィルターをどう決めているのか、という疑問も浮かぶと思います。その フィルターは人間でいちいち決めるのは難しいから、ニューラルネットワークに訓練データに基づいて決めてもらう のです。

ちなみにRGBを持つカラーの場合(=チャネル数3)は、フィルターがR,G,Bチャネルそれぞれに適用され、その合計値が出力されるため結果は以下図のようにグレースケールと変わらず1つのチャネルになっています。つまり、入力チャネル数がいくらであってもフィルター１つによって出力される画像は１つということです。このようにグレーでもカラーでも出力は変わらないので、ここからはまた入力をグレースケールに戻して考えます。

1.2 入力画像1枚、フィルター複数枚のCNN

通常、フィルターは1つだけではなく複数個使います。(人間の画像認識を超えたResNetでは64個や128個、512個のフィルターを1個の畳み込み層で使います。)ということで、ここではフィルターを4つ使った時にどうなるか見ましょう。

1枚の画像に4つのフィルターをそれぞれかけるのでその結果が得られます。
つまり、この 4つのフィルターによって1枚の画像が4つのチャネル(channel)を持つ ことになります。フィルター1つに対応して画像のチャネル(深さ、チャンネルとも言われる)が1つ出来上がります。

1.3 入力画像複数枚、フィルター1枚のCNN

また、入力画像についてですがこれも通常1枚だけでなく、複数枚を一気に処理します。この 複数枚のカタマリのことをミニバッチ と呼び、通常バッチサイズ(1カタマリの枚数)は16枚や32枚、64枚などです。マシンの性能が上がれば上がるほどこのミニバッチの大きさは大きくすることができます。ミニバッチにフィルターを1つだけかけてみます。

各画像にフィルターをかけて、各画像に対応した出力を得ます。
なんら難しいことはありませんね。

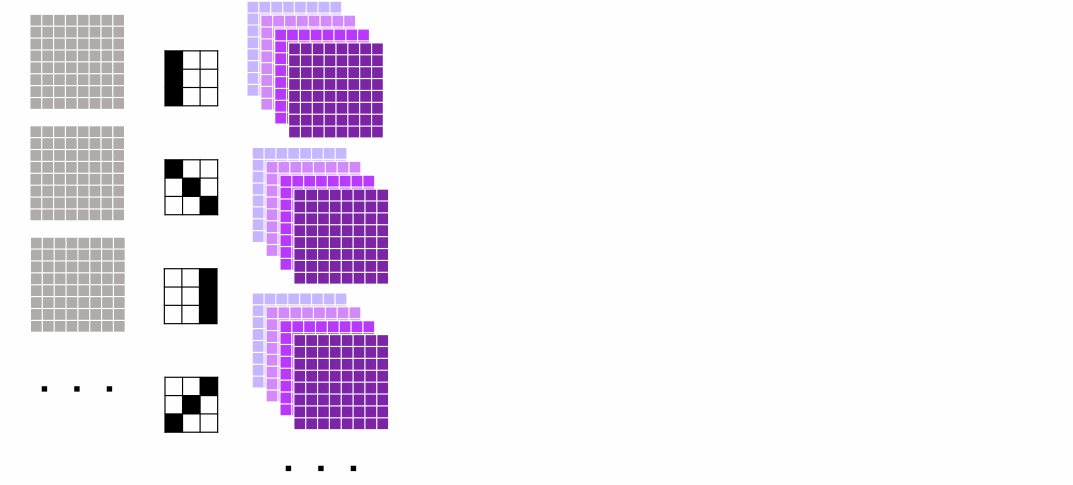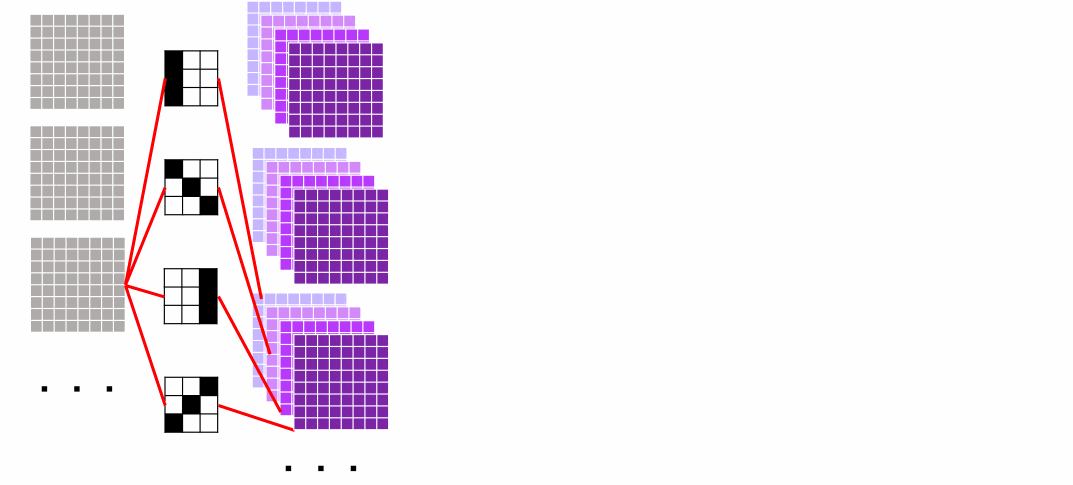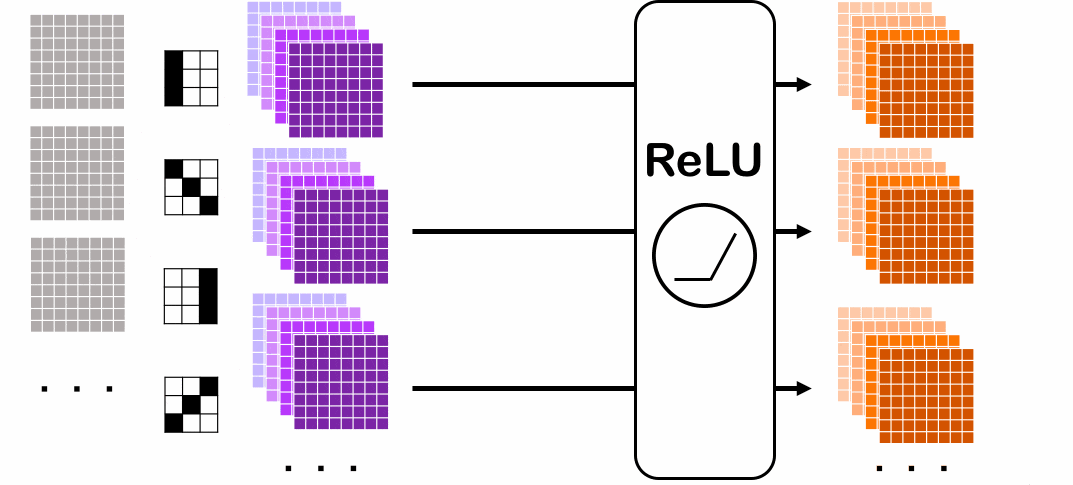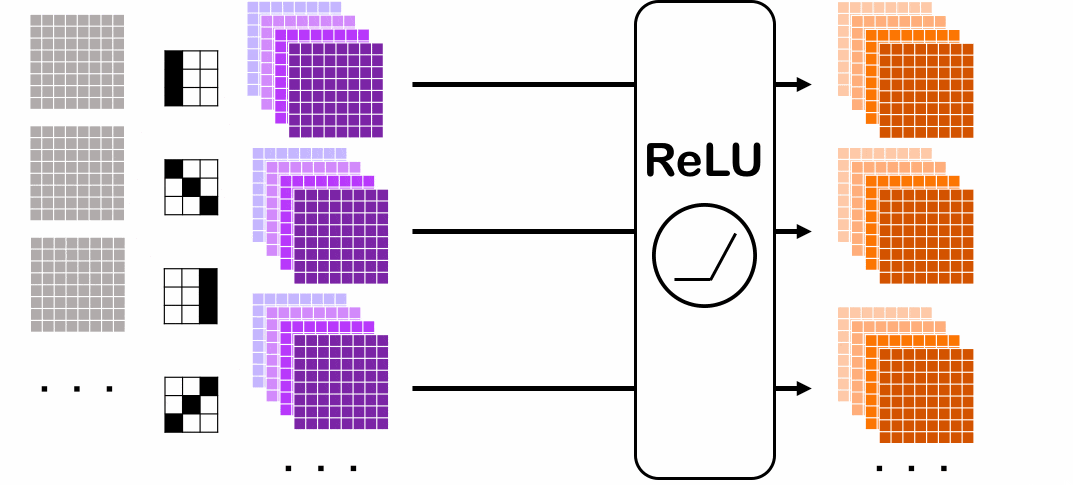
1.4 入力画像複数枚、フィルター複数枚のCNN

ということで、複数フィルターをかけた場合も考えましょう。
こちらも今まで通りで難しくはありません。

わかりやすさのために各フィルターとそれに対応した出力を赤線で引っ張ってみました。
それぞれの出力画像がフィルターの枚数に応じた4チャネルになっているだけです。
この出力が次の層の入力となります。

2. バッチノーマライゼーションとは？

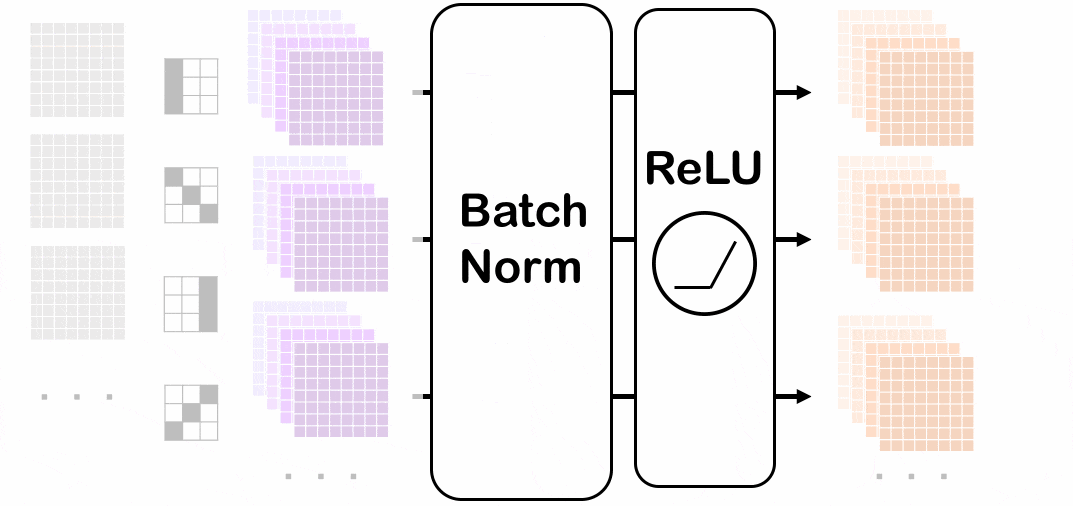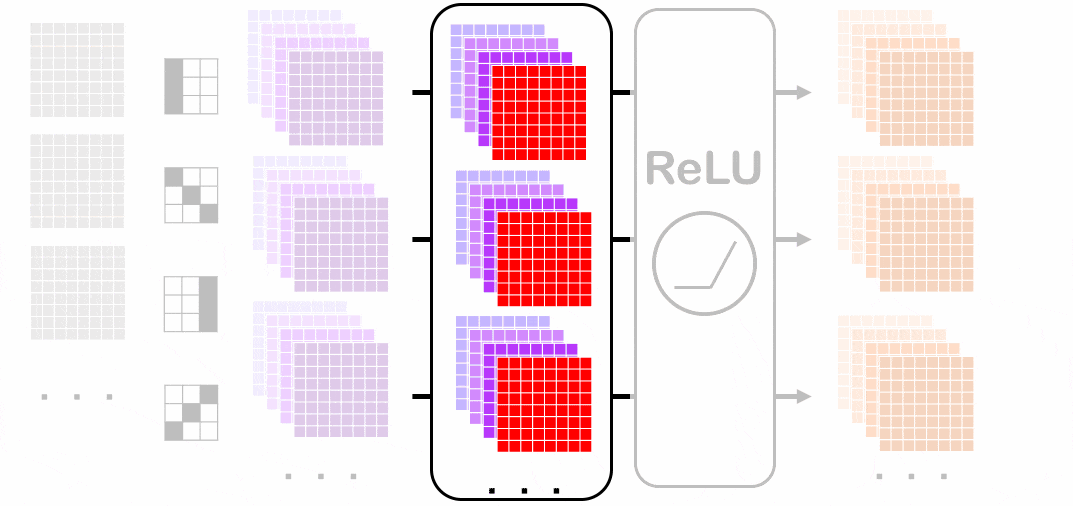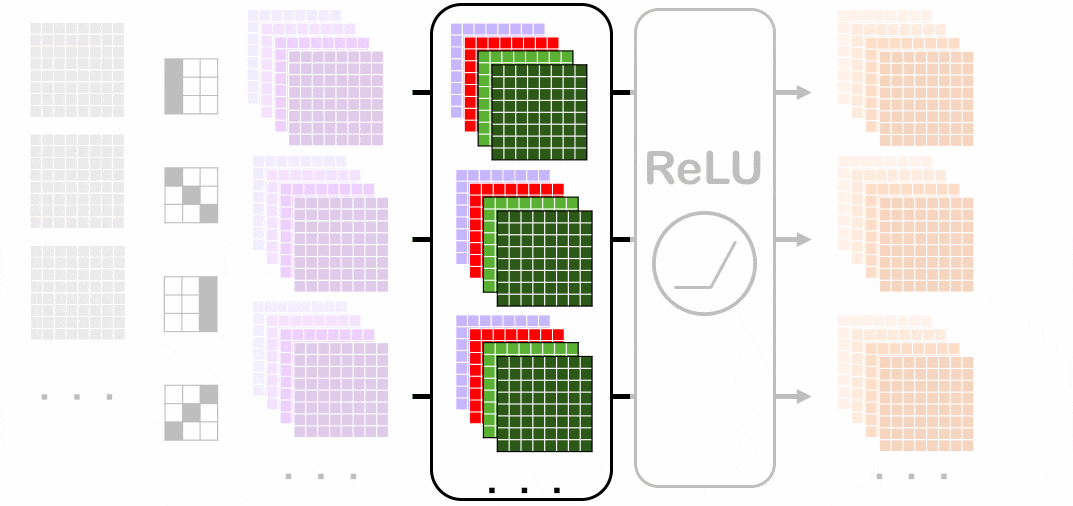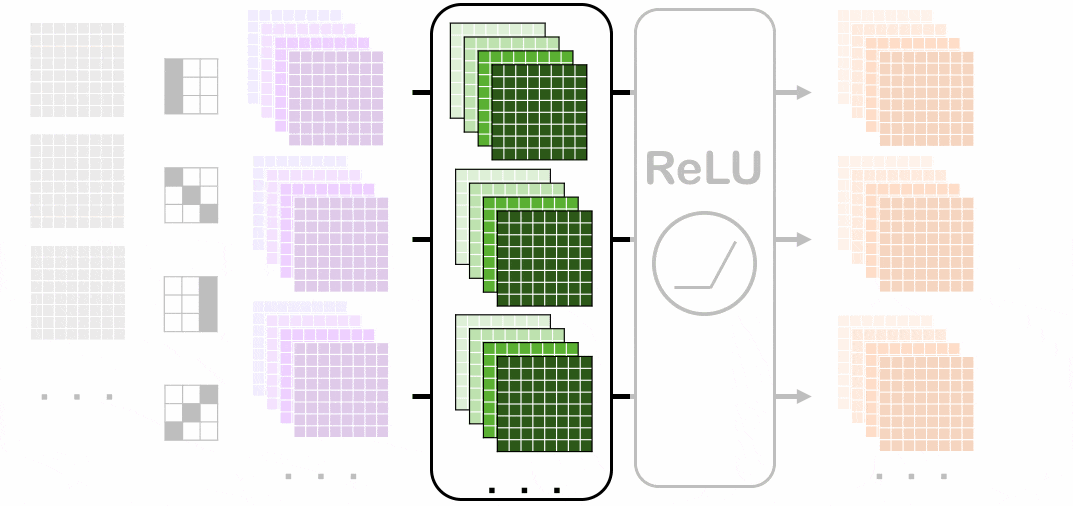
冒頭でも畳み込み層を何段も重ねて深くすることで精度を上げていくことを述べました。実際、8層しかなかったAlexNet(2012)に対して2014年には19層のVGG-19が発表され、2015年に発表されたResNetはなんと152層。このように層が深くなるとうまく学習ができなくなります。そこで導入されたのがバッチノーマライゼーション。処理内容は、1ミニバッチ内の全データの同一チャネルが平均0,分散1に正規化する こと。ミニバッチというのは1回に処理する複数画像のカタマリ でしたね。
正規化というのは データから全体の平均値を引いて、全体の標準偏差で割り算すること です。

バッチノームを適用させる前(紫色)から各チャネルごとにバッチノームを適用させていく経過を表しています。赤色になっているところでそれぞれ平均分散を出して正規化します(緑色が適用後)。

[注意]
「正規化する」≠「正規分布にする」ですので、お気をつけください。
正規化というのは単純にデータの線形変換なので、元のデータが従う分布を変えるわけではないのでご注意ください。

それでは、実際に原論文で提唱されたバッチノームの手順を見てみましょう。

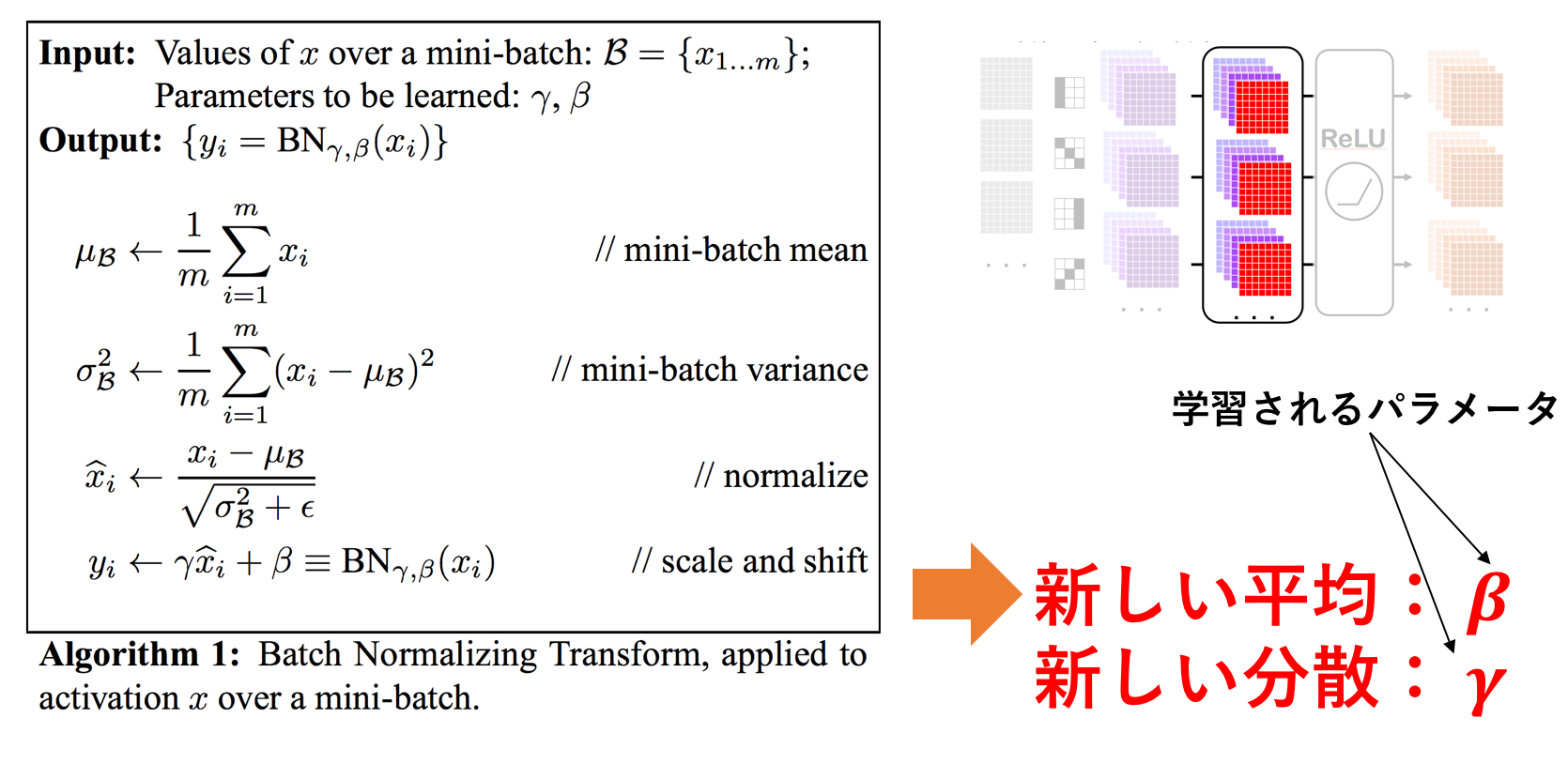
Ioffe, S. et al. "Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift" (2015)

3行目までは単純に正規化しているだけです。
1行目は平均、2行目は分散を取り、3行目で平均0分散1に正規化しています。ここの $\epsilon$ は分散が0の時にゼロ除算しないように設けられている非常に小さな値(=1e-3とか)です。
ただし、4行目で正規化した値に $\gamma$ をかけて $\beta$ を足しています。
これはどういう意味なのでしょうか。
平均0分散1のデータたちに対して $\gamma$ をかけて $\beta$ を足しているので、 ミニバッチのデータ(の各チャネル)は平均 $\beta$ 、分散 $\gamma$ を新しく持つことになります。この $\beta$ と $\gamma$ はデータで学習されるパラメータです。これらのパラメータを設けることでバッチノームで必ず平均0分散1にするのではなく、学習にあった平均と分散に従うように自由度をもたせている のです。

この手順を図に表したものも用意したのでご参照ください。
ミニバッチ内の一番手前のチャネルにバッチノームを適用させています。
スペースの都合上、特に一番上の画像におけるバッチノーム適用にフォーカスしています。

3. バッチノーマライゼーションの仲間たち

3.1 バッチノームの弱点

バッチノームというのはいまや当たり前のように使われており、優れた結果を出しまくっています。ただし、どんな術にも弱点となる穴は必ずある、と漫画NARUTOでうちはイタチが教えてくれたようにバッチノームにも弱点があります。それは以下の2つです。

• バッチサイズが小さいと使えない
  • 例えば極端な話バッチサイズが1だったら、もちろん正規化なんて無理。
  • エッジコンピュータなどリソースが限られているときはバッチサイズ大きくできないから問題になる。
• RNNなどの時系列データに使えない
  • RNNが時系列データに対して広く使われているのを考えると致命的！

3.2 バッチノームの仲間たち

上述した問題(特に1つ目)を解決するために出てきた代表的な手法が3つあります。
そちらを下図に表したので簡単に説明します。

一番左にミニバッチ、左から2番目に本稿の主人公バッチノーマライゼーションがいます。そしてそこから、**レイヤーノーマライゼーション、インスタンスノーマライゼーション、グループノーマライゼーション** と続きます。いずれもバッチノームと処理方法は同じで、1度に正規化する範囲が異なるだけです。(バッチノームは、ミニバッチ内の同一チャネルごとに正規化。)
ここでミニバッチ内のそれぞれのブロックは今まで通り画像データを表しているとします。
この例ではバッチサイズ3でデータのチャネル数が4です。赤色になっている部分がノーマライゼーションを適用する際の平均と分散を計算する箇所を表しています。

いずれもバッチノームが持つ、バッチサイズに下限(通常16以上)を設けてしまうという欠点に対して提案されており、派生手法はいずれもバッチ方向ではなく、チャネル方向に対して正規化されていることがわかります。バッチノームのバッチサイズへの下限を克服するためにまず提案されたものが レイヤーノーム と インスタンスノーム です。レイヤーノームは1つのデータの全チャネルに対して正規化 を行い、インスタンスノームは1つのデータの1つのチャネルに対して正規化 を行います。そしてこれらの中間のようなものとして発表されたものが グループノーム で、これは 1つのデータの任意のチャネル数に対して正規化 したものです。ここまで読んでもう一度上図を見るとわかりやすいと思います。

上図においてグループノームで1グループのサイズを4に設定すれば、レイヤーノームと同じで逆に1に設定すればインスタンスノームと同じことになります。

3.3 一体どれを使えばいいんだ。

答えは簡単です。
バッチノーム一択

実はいずれの方法もバッチノームの性能を越えることができていないのですね。
あくまでもバッチサイズが小さい時にしかバッチノームよりも良い効果を発揮しない、ということです。ただ、それぞれ実用で使われている例がありますのでそちらを紹介してこの節を締めたいと思います。

• レイヤーノーム: RNN系やTransformer
• インスタンスノーム: GAN系(StyleGAN)
• グループノーム: 画像認識系(に良いらしい。(GNの原論文))

4.(オプション)なんでバッチノーマライゼーションって強いの？

ニューラルネットにおける勾配降下法やバックプロパゲーションなどをある程度理解していることを前提に書きましたので、よくわからなければ読み飛ばしてもらって構いません。
ここで言っていることは簡単にまとめると、以下の2点だけです。

• バッチノームがうまくいく理由はまだわかっていない。
• でもどうやらバッチノームのおかげでニューラルネットにとってタスクが簡単になっているのだろう。

ここからは上記2点についてもう少しだけ補足します。

バッチノームが良い理由として内部共変量シフト(= ICS, Internal Covariance Shift)の解消が原論文では言われています。ICSとは単純に ニューラルネットの層を過ぎる毎にその層のアウトプットの分布が変わるよ、ということ。ニューラルネットの中を通るデータの分布が頻繁に変わってしまっては学習しづらいよね、という問題。(だと理解している。間違っていればコメントお願いします。)バッチノームはこのICSを解決しているため精度向上に寄与している、という主張が原論文によってされているわけです。ただし実際はこの主張は間違っているということがわかっています。つまり、バッチノームによってICSは解決されない のです。

ではなぜバッチノームが強いのか。その理由は実はまだわかっていません。
ただ、１つの可能性として、バッチノームはチェックポイントとして働いている という説明がIan Goodfellow氏(GAN作った人！)によってされています。

まず、活性化関数を持たない単純なニューラルネットを考えます。
各丸が全結合層で、i 回目のイテレーションと(i+1) 回目のイテレーションを表しています。
イテレーションの定義はフィードフォワードとバックプロパゲーションの1セットです。

ここでm層に注目すると(i+1) 回目のイテレーションの重み $w^{i+1}_m$ は 前(i 回目)のイテレーションのLossを使って更新されているため、i 回目におけるm層よりも前層の重みたち(つまり、 $w_l^{i}, w_k^{i}, ...$ )に対して最適化されています 。ただし、 (i+1) 回目の時のフィードフォワードは $w_l^{i}, w_k^{i}, ...$ ではなく、更新された $w_l^{i+1}, w_k^{i+1}, ...$ を使って予測値を出します。つまり、ある重みを更新する時には、本来その前の層の重みたちがどう更新されるのかということも考慮しなければ最適な値は求められないのですが、一階微分だけを用いている勾配降下法ではこのような複雑な関係性まで考慮できません。この複雑な関係性の救世主がバッチノームです。

バッチノームをいれてみましょう。

再びm層に注目します。バッチノームにより、m層への入力値は正規化されています。m層以前の層による値がどうであろうと一旦バッチノームで調整されてm層へと入力されるのです。これはつまり、m層の重みはもはやm層以前の全ての重みたちを考えるのではなく、直前のバッチノームのパラメータ $\gamma, \beta$ だけを考えれば良い のです。このことにより大量の重みたちによる複雑な関係性を考慮しなくていいため、ニューラルネットが学習しやすくなり精度や速度があがる、ということです。これがIan Goodfellow氏によるバッチノームがうまくいく理由です。

5.まとめと所感

今までなんとなくバッチノームを使っていたのですが、今回調べたおかげで効果や仲間たちがわかりました。バッチノームのことを理解するために、重みの初期化や活性化関数、最適化関数の意義なども今までより深く理解することができたのでそちらも需要があればアウトプットしていきたいと思っていますのでよろしくお願いします。

読んで少しでも何か学べたと思えたら 「いいね」 や 「コメント」 をもらえるとこれからの励みになります！よろしくお願いします！
(間違いなどもございましたら、ご指摘よろしくお願いします。)

6.参考

• Batch Normalizationとその派生の整理
  Batch Normalizationの概要とその派生たちを簡単に理解できた。だいぶ参考にしています。

• Normalizing Activations in a Network (C2W3L04)
  (英語) Andrew Ng氏によるわかりやすいBN解説動画。数式とともに解説してくれている。

• Intro to Optimization in Deep Learning: Busting the Myth About Batch Normalization
  (英語) BNがなぜ必要でなぜ有効なのかというのをわかりやすく教えてくれている。

• An Overview of Normalization Methods in Deep Learning
  (英語) BNの派生たちを教えてくれている。

• Understanding Batch Normalization
  (論文) バッチノームが内部共変量シフトを解決しているわけではないという旨が書かれている。

• An Intuitive Explanation of Why Batch Normalization Really Works (Normalization in Deep Learning Part 1)
  (英語) バッチノームがニューラルネットのHigher-order interactionを緩和させていることが書かれている。