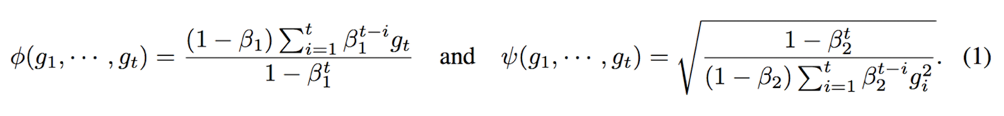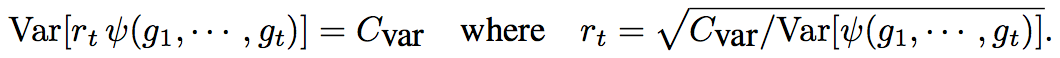オミータです。ツイッターで人工知能のことや他媒体で書いている記事など を紹介していますので、人工知能のことをもっと知りたい方などは気軽に@omiita_atiimoをフォローしてください!
最新の最適化アルゴリズムRAdam
ニューラルネットワークは画像認識や自然言語処理など多方面で使われており、おもしろいことにも使うことができます。そんなニューラルネットワークが高い精度を出すためには、優秀な最適化アルゴリズムが必要不可欠です。最適化アルゴリズムとして現在デファクトスタンダードとなっているのがAdamです。Adamが登場したのは2014年のことですが、そこからAdamに取って代わるような最適化アルゴリズムは久しく出ていません。そんな現状をとうとう変えると期待されている新しい最適化アルゴリズムの論文が国際学会ICLR2020に採択されました。その名もRectified Adam、通称RAdamです。画像認識のImageNetやCIFAR-10に加え機械翻訳のIWSLT'14でAdamよりも優れた性能 を示しており、GitHubでの論文筆者による実装はすでに2,000を超えるスターを獲得しており、かなり注目されていることがわかります。本記事ではそんな期待されているRAdamの論文を徹底解説 していきます。
読んで少しでも何か学べたと思えたら 「いいね」 や 「コメント」 をもらえるとこれからの励みになります!よろしくお願いします!
流れ
- 忙しい方へ
- 論文解説
- まとめと所感
- 用語と補足
- 参考
原論文:On the Variance of the Adaptive Learning Rate and Beyond, Liu, L. et al. ICLR 2020
0. 忙しい方へ
- 画像分類のImageNetやCIFAR-10から機械翻訳のIWSLT'14やWMT'16などの幅広いタスクおよびデータセットでRAdamがAdamよりも優れた性能
- 学習の初期段階でAdamの適応学習率の分散が大きくなりすぎるという問題があることを指摘
- ヒューリスティックな手法で、ハイパラ調整を必要とするWarmupは上記の問題を緩和することを発見
-
適応学習率の分散を自動的に抑えられるような機構をAdamに組み込んだものがRAdam(ハイパラ調整不要!)
- ステップ数が4以下: 適応学習率を使わない(=ただのモーメンタム付きSGD)
- ステップ数が4よりも大きい: Adamに補正項をかける ことで適応学習率の分散を抑える
- RAdamの大体のアルゴリズムは以下のような感じ
こちらの記事もどうぞ:
- 「募ってはいるが、募集はしていない」 人たちへ: 自然言語処理を使った記事です。
1. 論文「On the Variance of the Adaptive Learning Rate and Beyond」解説
1.0 要約
RMSPropやAdamはSGDに適応学習率を導入した最適化アルゴリズムであるが、学習の初期段階では適応学習率自体の分散が極端に大きくなってしまいとんでもなく大きい値を取りかねない。学習率に対するヒューリスティックであるWarmupはこれを緩和していることがわかった。そこで、適応学習率の極端な分散を自動的に抑えるRectified Adam(RAdam)を提案。
1.1 導入
最適化アルゴリズムには「速度」と「安定性」が常に求められてきた。そこで近年開発されたのが 適応学習率 である。適応学習率とは勾配の大きさに従って学習率を適宜調整するもの で、AdagradやRMSProp、Adamなどが素早く収束するのに貢献している。そんな適応学習率を使った最適化アルゴリズムたちの性能をさらにあげるために Warmup が広く用いられている。Warmupとは学習の初期段階を通常よりも小さな学習率で始め、学習が進むにつれて徐々に通常の学習率まで上げていくヒューリスティックな手法 である。
この論文では次の2つがメインとなる。
- 学習初期段階における 適応学習率の問題 を見極め、Warmupの有効性 を理論的に考察
- 適応学習率の問題点を解決する 新たな最適化アルゴリズムRAdam を提案
1.2 前置きとモチベーション
1.2.1 Adamの適応学習率
AdamはSGDに「モーメンタム」と「適応学習率」を組み合わせたもの である。このモーメンタムと適応学習率をそれぞれ式で表すと、次式のようになる。ここで前者がモーメンタムの式で、後者が適応学習率の式である。
ここで、$\beta$ はハイパーパラメータで、$g_t$ は勾配を示す。本論文では 適応学習率にのみ注目しているため2つ目の式 $\psi(\cdot)$ だけを考えていく。
1.2.2 Warmup
Warmupとは、最初の学習率を通常よりも小さく設定し徐々に通常に学習率まで上げていくもの。どう上げていくかなどはハイパーパラメータであるため、試行錯誤で最適なものを見つけなければならない。Adamなどと併用することで精度向上ができる。これを通常の学習率スケジューラと比較すると以下図のようになる。横軸がステップ数で縦軸が学習率、オレンジ色の線がWarmupを示している。
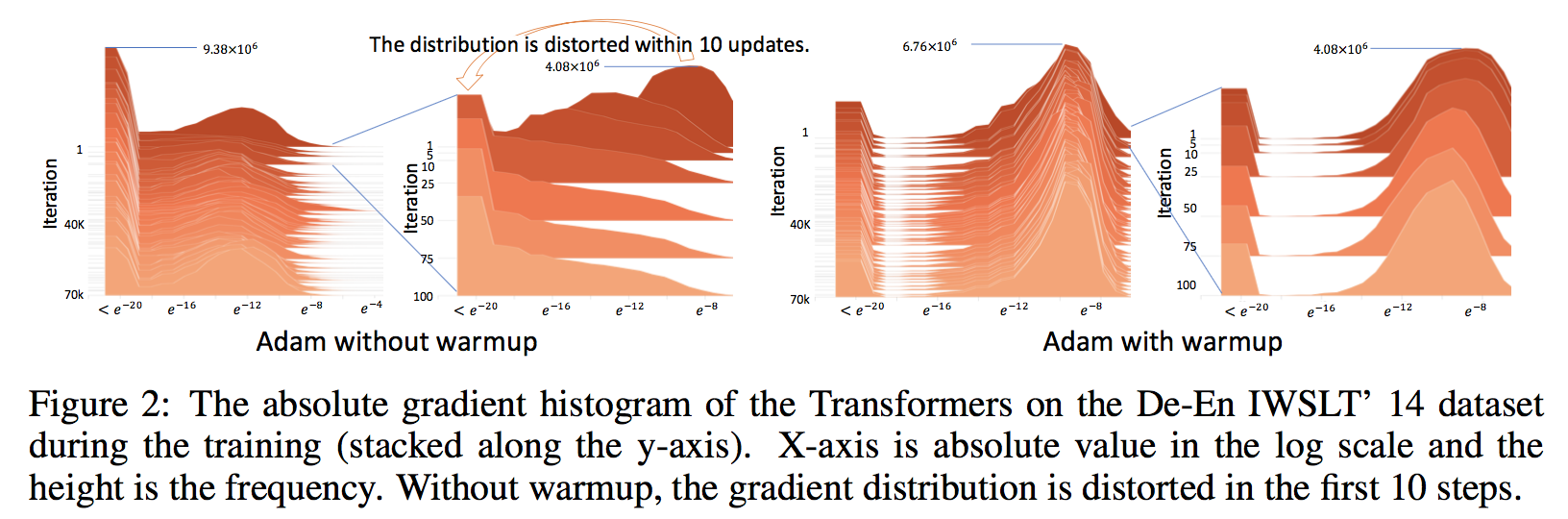
続いてWarmupがある場合とない場合の勾配にどう違いが出るかを見る。Transformer[解説]をモデルとしてDe-En IWSLT'14データセットに対しての勾配のヒストグラムを各ステップに対して示す。
左図がwarmupがない場合で、右図がwarmupがある場合。warmupがない場合はわずか10ステップほどで勾配がほぼゼロになってしまっている。これはAdamが粗悪な局所的最適解に陥ってしまっていることを意味している。一方でwarmupがある場合だと勾配はゼロにならず値を持つことができている。
1.3 適応学習率の分散
ここでは学習の初期段階ではサンプル数が少ないために、適応学習率の分散が極めて大きくなり粗悪な局所的最適解に陥っている、という仮定を確かめるための実験的証拠を示したのちに、適応学習率の分散について分析 する。
詳しく見る前に、ステップ数が小さい時に適応学習率の分散が極めて大きくなってしまうことについて直感的に理解してみる。そのため、ステップ $t=1$ の時を考えると、 $\psi(g_1)=\sqrt{\frac{1}{g^2_1}}$ である。$g_1\sim\mathcal{N}(0,\sigma^2)$ とみなすと、$\frac{1}{g_1^2}$ は $\mathrm{Scale}$-$\mathrm{inv}$-$\chi^2(1,\frac{1}{\sigma^2})$ に従うため、適用学習率の分散 $\mathrm{Var}[\sqrt{\frac{1}{g^2_1}}]$ は発散することがわかる。これが意味しているのは、学習の初期段階では適用学習率があまりにも大きな値を取ってしまいかねない、ということである。(と、理解している。)
1.3.1 分散抑制としてのWarmup
Adamの適応学習率の分散を明示的に抑えるためにその発展系を次の2つ定義する。:
- Adam-2k: 最初の2,000ステップは 重みやモーメンタムなどは更新せず、適応学習率だけ更新 していく。その後、通常のAdamと同じように更新する。
- Adam-eps: 適応学習率の式 $\frac{\sqrt{1-\beta^t_2}}{\epsilon + \sqrt{(1-\beta_2)\Sigma^t_{i=1}\beta^{t-i}_2g^2_i}}$ における $\epsilon$ を大きい値 $10^{-4}$ に設定 する。(通常は $10^{-8}$ 程度。)
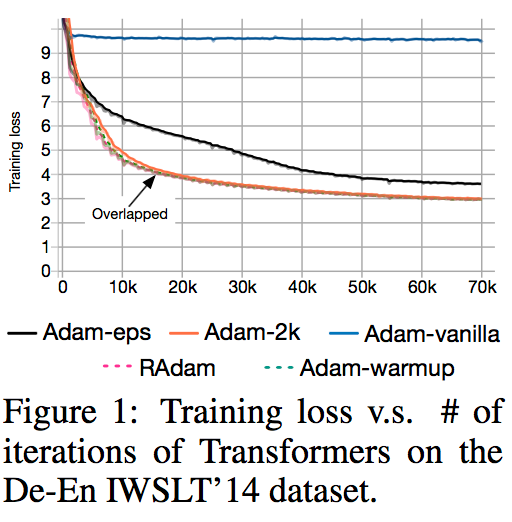
これらのDe-En IWSLT'14データセットに対する損失は以下図のようになる。通常のAdamが苦戦している一方で Adam-2kとAdam-epsはしっかりと学習しており、適応学習率の分散を抑えることが重要 であることがわかる。
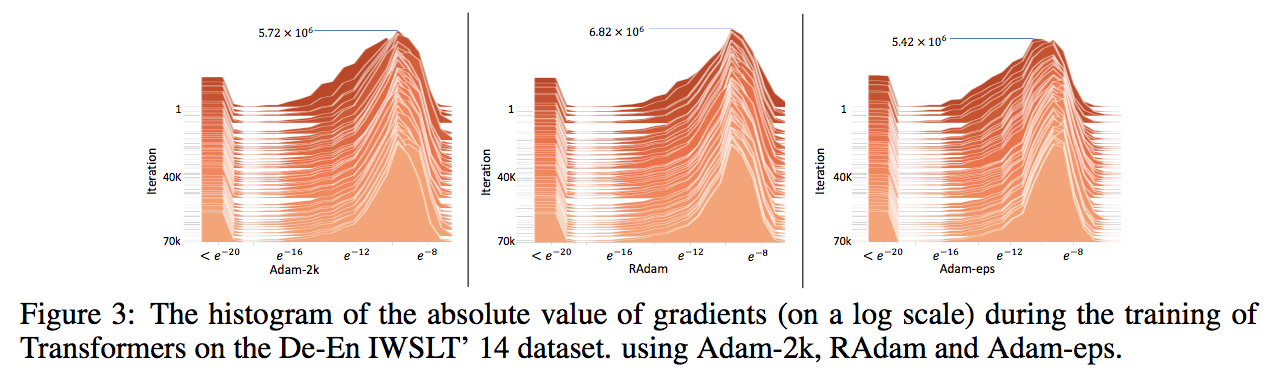
また、これらについて以下図の勾配のヒストグラムを見てみても Warmupと同様に勾配の値をしっかりと持つことができている。
1.3.2 適応学習率の分散の分析
適応学習率の式は単純に勾配の2乗の(指数平滑)移動平均であり、学習の初期段階(つまり、$t$ が小さい時)は指数平滑移動平均は通常の平均に近似することができる ため、次式が成り立つ。
ここで、$g_i \sim \mathcal{N}(0,\sigma^2)$ であるため、$\frac{t}{\Sigma^t_{i=1}g^2_i}\sim\mathrm{Scale}$-$\mathrm{inv}$-$\chi^2(t,\frac{1}{\sigma^2})$ であると言える。つまり、適応学習率が自由度 $\rho$(=学習のサンプル数に等しい) のスケール逆カイ二乗分布に従う ため、自由度 $\rho$ つまりサンプル数が増えるにつれて適応学習率の分散は減っていく。(証明は論文Appx.Aを参照)
ちなみに、解析的には適応学習率の分散は $\forall\rho>4$ で次の式になる。
1.4 補正適応学習率(Rectified Adaptive Learning Rate)
ここでは自由度 $\rho$ を推定したのちに、学習率の補正項を考える。
1.4.1 自由度推定
ここでは移動平滑平均を単純移動平均で近似すると、$\rho_t = \frac{2}{1-\beta_2}-1-\frac{2t\beta^t_2}{1-\beta^t_2}$ が得られ、また $t$ を無限に飛ばすことで $\rho_\infty=\frac{2}{1-\beta_2}-1$ も得られる。
1.4.2 分散推定と補正項
1.3.2よりサンプル数が増えると適用学習率の分散が小さくなるため、適用学習率の分散の最小値 $C_{var}=\mathrm{Var}[\psi(\cdot)]\mid_{\rho_t=\rho_\infty}$ である。ここで、適用学習率を常に一定値 $C_{var}$ にしておくには次のような $r_t$ があれば良い。
この式において、$\mathrm{Var}[\psi(\cdot)]$ がわかれば、$r_t$ が求められるものの1.3.2の式(2)は解析的に扱うのが難しいため、代わりに $\sqrt{\psi^2(\cdot)}$ をテイラーの一次で展開することで扱いやすい $\mathrm{Var}[\psi(\cdot)]$ が得られ、結果として補正項 $r_t$ は下図になる。
こうして、とうとうお待ちかねのRAdamのアルゴリズムが下図のように完成。
とても複雑に見えますが、Adamとの処理的な違いは赤枠で囲ったところだけで、赤枠で囲ったところは冒頭で出した図とほぼ同義。
1.5 実験
1.5.1 Adamとの比較
1.5.1.1 言語モデル(One Billion Word)
言語モデルにおけるパープレキシティはRAdamがAdamよりも良い性能 を示している。
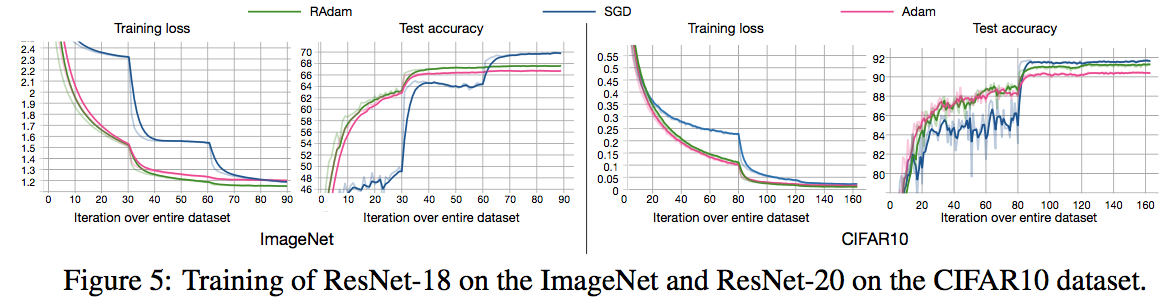
1.5.1.2 画像分類(ImageNetとCIFAR-10)
ImageNetおよびCIFAR-10でRAdamの方がAdamよりも高い精度 を示している。最終的な精度を表で表すと以下。
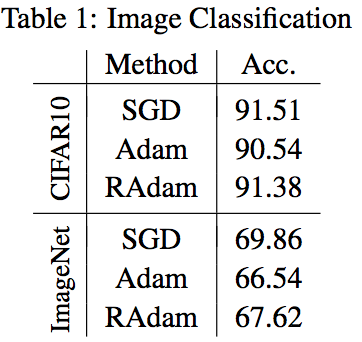
RAdamはAdamよりも高い性能を示しているが、SGDがかなり強い ことがわかる。
また、CIFAR-10に対する学習率ごとの精度を比較すると以下図。
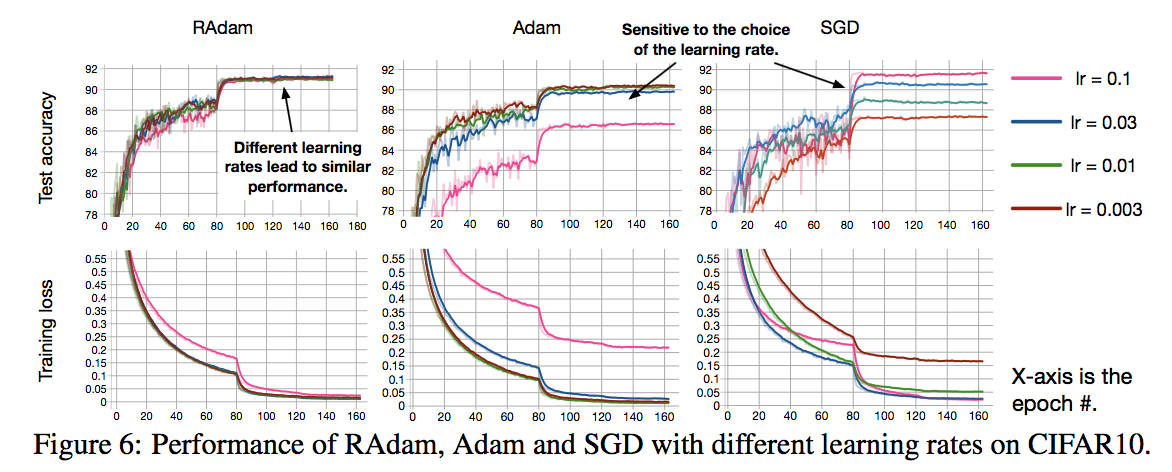
RAdamがいずれの学習率でも安定して高い精度を叩き出せている ことがわかるが、特にSGDは学習率によって精度が大きくばらつき安定しないことがわかる。
1.5.2 Warmupとの比較
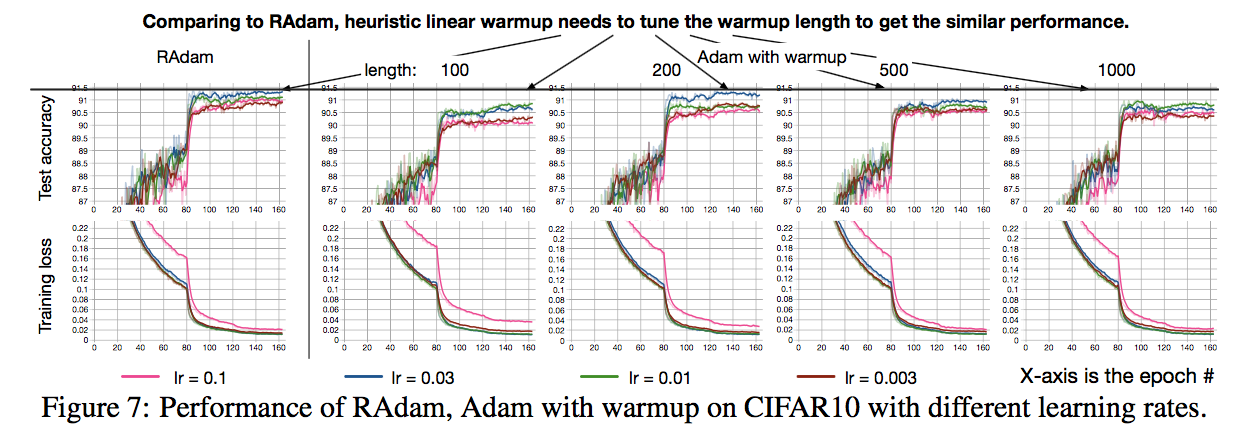
1.5.2.1 画像分類(CIFAR-10)
RAdamはハイパラ調整をする必要がないが、Warmupはハイパラを調整することでRAdamと同程度の精度 となっており、RAdamの有用性 がわかる。
1.5.2.2 機械翻訳
機械翻訳においてもRAdamがWarmupの代わりをしっかりと担えていることがわかる。
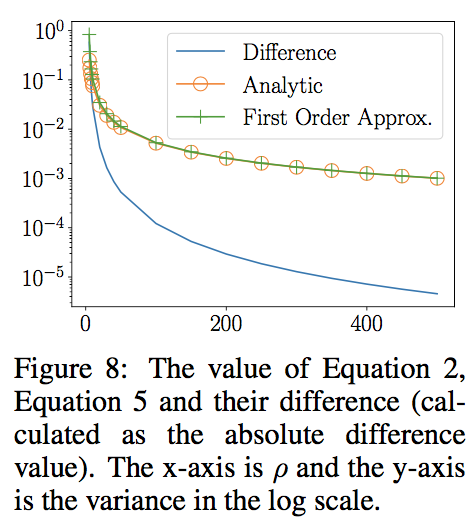
1.5.3 近似の検証
1.4.2において、適応学習率の分散をテイラーの一次展開で近似したが、それによる影響がほぼないことが下図で示されている。近似による誤差(青線)が極めて小さい ことがわかる。
1.6 結論
学習の初期段階で適応学習率の分散が極めて大きくなり、粗悪な局所的最適解に陥ってしまうことがわかった。そして、実験的かつ理論的に分析することでその問題を解決する最適化アルゴリズムRAdamを提案。実験を通しRAdamの有用性を示せた。
2. まとめと所感
ヒューリスティックなWarmupを足がけに、適応学習率の分散を抑えることで高い性能を示したRAdam。余談ですが、この論文筆者の方はMicrosoftにインターン中に書いたようで、素直にとんでもないと思いました。実際に試してみたい方は実装を簡単に試せるので使ってみてはいかがでしょうか!
ツイッターで人工知能のことや他媒体で書いている記事など を紹介していますので、人工知能のことをもっと知りたい方などは気軽にフォローしてください!