概要
前回の記事はこちら
本記事では過学習抑制のための手法の代表的なものの一つであるドロップアウトについて説明します。簡単な手法ながらその効果は提案されてから今に至るまで使い続けられていることから察することができるでしょう。
ちなみに過学習を抑制できる理論的説明は未だされていないっぽいです。(調査不足かも...)
いろいろ理由は考えられていますがね〜
更新履歴
- 2020/10/8
- 比較器を実装しました。
目次
ドロップアウトとは
ドロップアウト: Dropoutは過学習を抑制する手法として2012年に提案され、かの有名なAlexNetでも採用されました。
概要としては「学習時に全結合層の各層の出力をある確率$ratio$でシャットアウトする」だけです。たったこれだけで過学習が抑制されるというので驚きです。
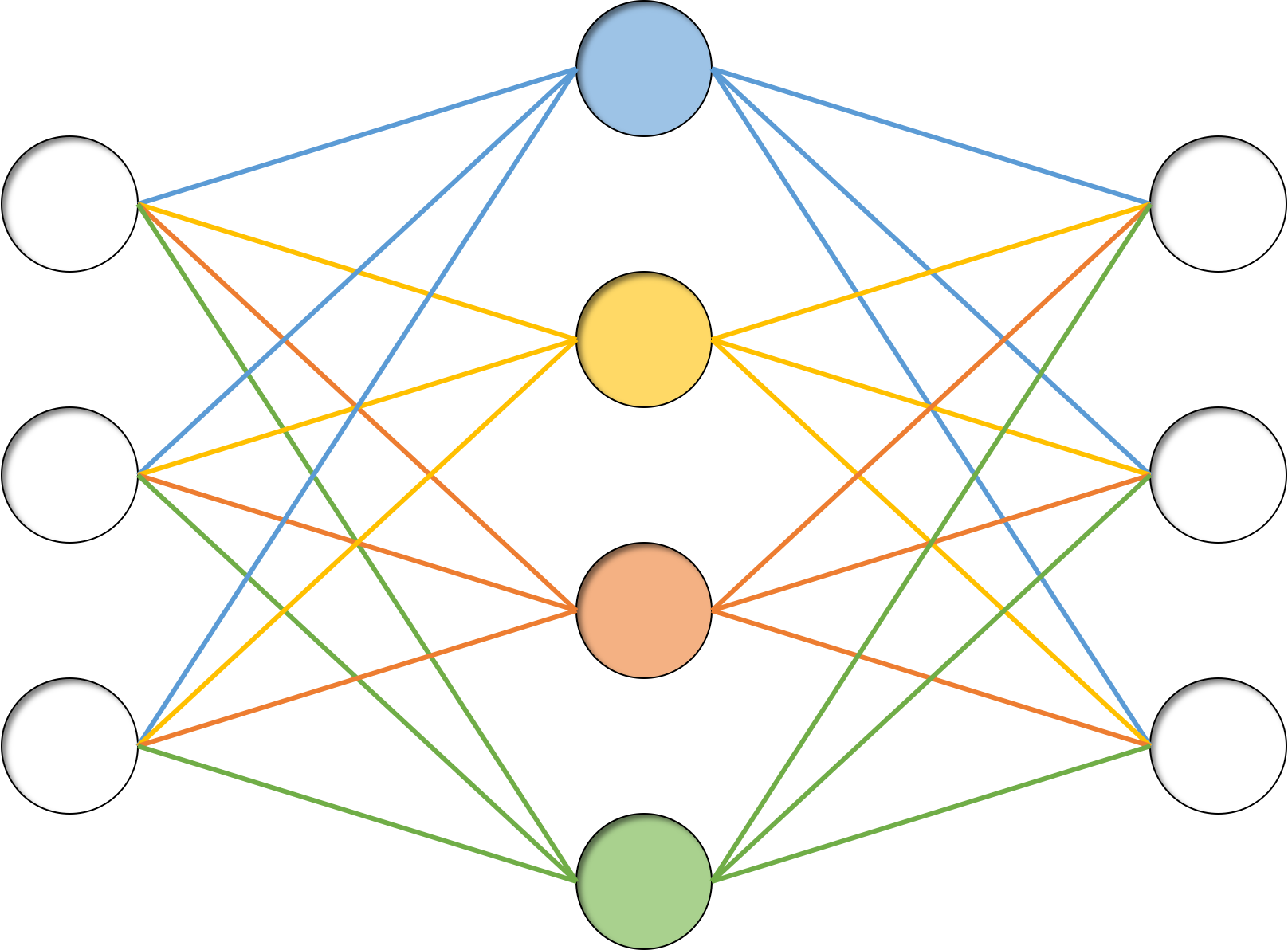
どうして過学習が抑制されるのかについての理論的説明はされていないと思いますが、いろいろと理屈づけはされています。その一つがアンサンブル学習です。
アンサンブル学習との関係
そもそもアンサンブル学習とは、複数の弱学習器を統合して高精度を実現する技術のことです。
ドロップアウトが特に関係するのはそのうちバギングという手法になります。
詳しくはここで簡単に触れていますのでそちらを参照してください。
ともあれドロップアウトは複数のモデルを同時に学習していくことになるので、ある種バギングと同じようなことが行われています。
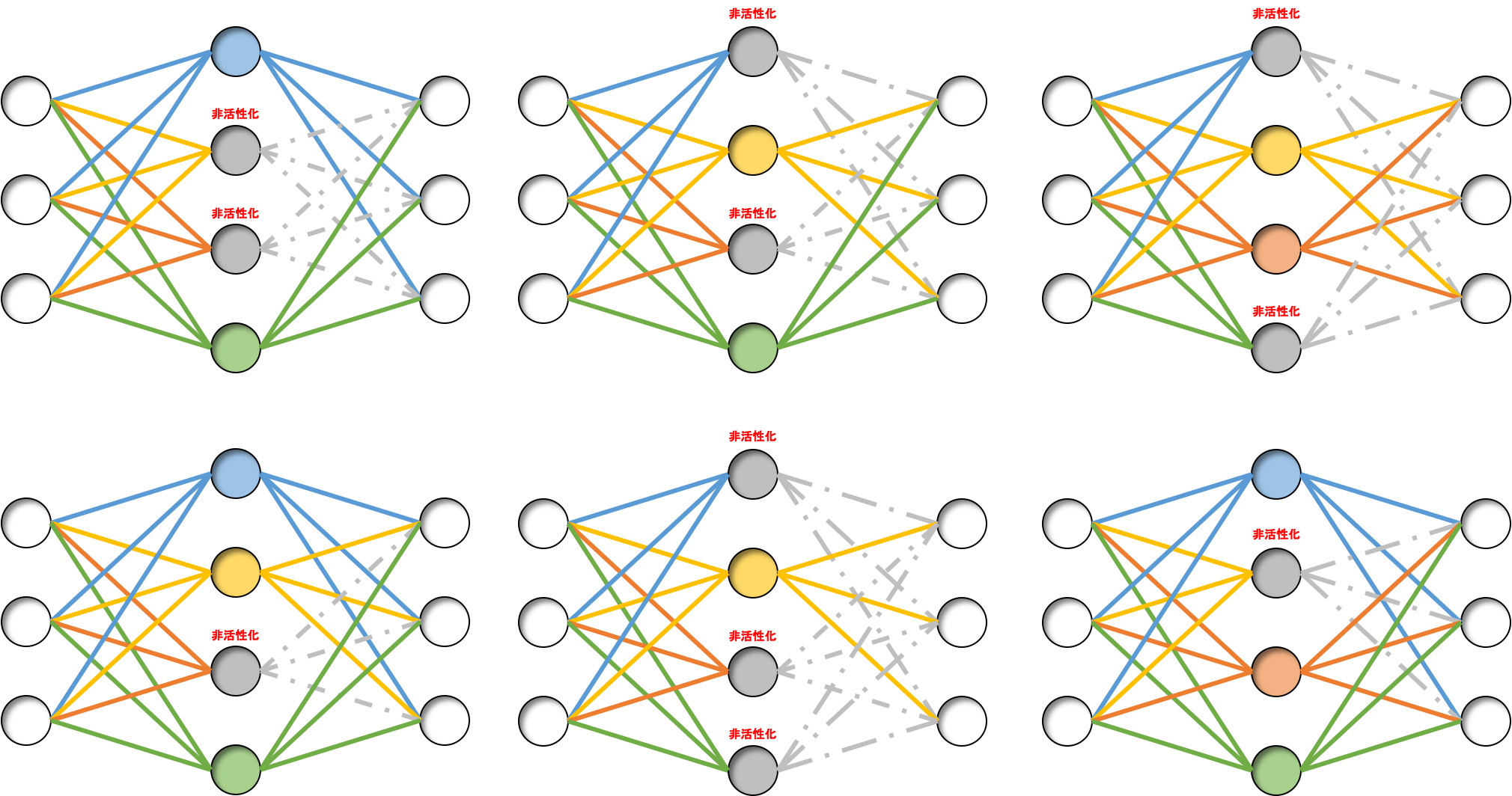
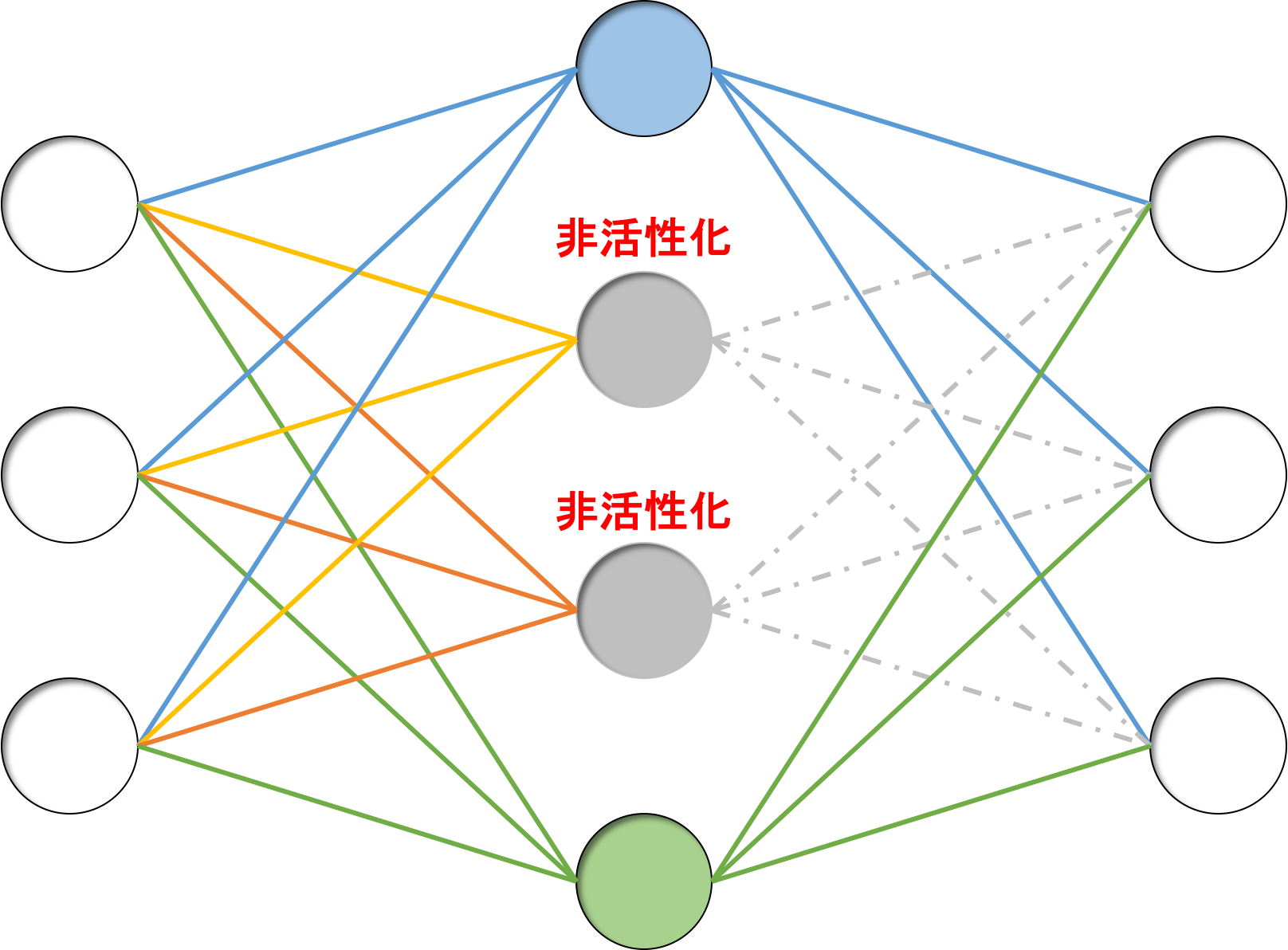
非活性化するニューロンが毎回の学習時に異なっていることで、それぞれのパターンで別々のモデルを学習していくことになり、つまり異なるモデルを学習している、とみなすことができます。
このことから、複数の学習器による学習=アンサンブル学習が擬似的に行われていると考えられます。
バギングの特徴として、学習結果が高バイアス低バリアンスになることが挙げられるため、ある程度纏まりつつも学習データに完全にフィッティングしないことになります。
よって、過学習が抑制されると考えられています。
実装を理論から見る
さて、実装を簡単に理論から見てみましょう。
先に述べたとおり、ドロップアウト層は「学習時に全結合層の各層の出力をある確率$ratio$でシャットアウトする」だけですので、実装そのものは簡単です。
しかし、鋭い方は気付いているかもしれませんが、「学習時に」というのが焦点になります。
では学習を終えて、推論に入った場合はどういうことになるのでしょうか。
推論時はドロップアウトしませんので、全てのニューロンが活性化状態のままです。
なんとなく想像がつくと思いますが、こうなると学習時と推論時の出力の「濃度」が異なることになります。
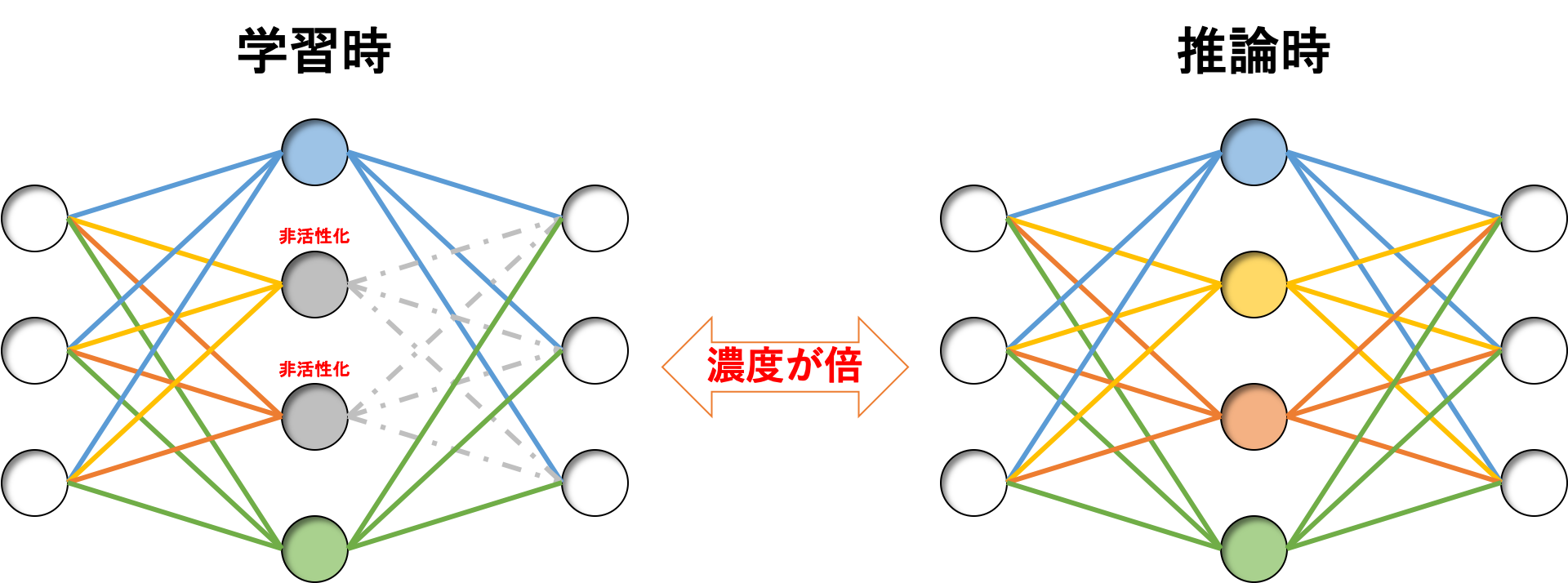
これを解消するために、推論時は出力を$(1 - ratio)$倍するという方法があります。
少し数式で見てみましょう。
ドロップアウト適用前の出力を$y$、適用後の出力を$\hat{y}$とすると、学習時の出力の期待値は
\mathbb{E}[\hat{y}] = \underbrace{(1 - ratio) y}_{活性ニューロンの期待値} + \underbrace{ratio \times 0}_{非活性ニューロンの期待値} = (1 - ratio)y
のようになります。
これに対して推論時は切り捨て率$ratio$は0となり、その出力の期待値は
\mathbb{E}[\hat{y}] = \underbrace{(1 - 0) y}_{活性ニューロンの期待値} + \underbrace{0 \times 0}_{非活性ニューロンの期待値} = y
となり、$\frac{1}{1 - ratio}$倍出力が「濃く」なっています。(ここで$ratio$は$0 \le ratio \lt 1$であることに注意してください)
この「濃さ」を調整するように推論時の出力を$(1 - ratio)$倍することでこのミスマッチを解消しよう、ということです。
(1 - ratio) \mathbb{E}[\hat{y}] = (1 - ratio) \left\{ \underbrace{(1 - 0) y}_{活性ニューロンの期待値} + \underbrace{0 \times 0}_{非活性ニューロンの期待値} \right\}= (1 - ratio)y
しかしこれは安直で危うい方法になります。
もちろんこのままでも特に問題なく学習できますし、推論も問題なく行えます。
ただ、この方法は「推論の出力を変更する」という危険を孕んでいます。
それが問題になる場面はあまり無いと思いますが、推論フェイズの出力はモデルの精度評価に用いられるため触らないに越したことはないのです。
ではどうするかというと、「学習時の出力の方を推論時のそれに揃える」という方法があります。
つまり、学習時の出力を$(1 - ratio)$で割ることでその濃度を「濃く」します。
\cfrac{1}{1 - ratio}\mathbb{E}[\hat{y}] = \cfrac{1}{1 - ratio} \left\{ \underbrace{(1 - ratio) y}_{活性ニューロンの期待値} + \underbrace{ratio \times 0}_{非活性ニューロンの期待値} \right\} = y
こうすることで出力の期待値が学習時と推論時で揃うため、推論時に出力を触る必要がなくなります。
このように学習時の出力を弄る手法は、通常のドロップアウト法に対して逆ドロップアウト法と呼ばれています。
ドロップアウト層の実装
では、逆ドロップアウト法でドロップアウト層を実装します。
class Dropout(BaseLayer):
def __init__(self, *args,
mode="cpu", ratio=0.25,
prev=1, n=None, **kwds):
if not n is None:
raise KeyError("'n' must not be specified.")
super().__init__(*args, mode=mode, **kwds)
self.ratio = ratio
self.mask = self.calculator.zeros(prev)
self.prev = prev
self.n = prev
def forward(self, x, *args, train_flag=True, **kwds):
if train_flag:
self.mask = self.calculator.random.randn(self.prev)
self.mask = self.calculator.where(self.mask >= self.ratio, 1, 0)
return x*self.mask/(1- self.ratio)
else:
return x
def backward(self, grad, *args, **kwds):
return grad*self.mask/(1 - self.ratio)
def update(self, *args, **kwds):
pass
実装はシンプルですね。
出力のニューロン数は前の層に一致させる必要があるため初期化の段階ではじいています。
順伝播については、学習時はmaskという変数でランダムにドロップアウトするニューロンを選択しています。また、出力時に$(1-ratio)$で割り算することで逆ドロップアウトを実現しています。
そのため、推論時はそのまま素通りする実装となっています。
逆伝播は学習時にしか使用しないため順伝播のように処理を分ける必要はありません。活性ニューロンだけ逆伝播するように順伝播時と同じmaskを要素積で乗算し、また$(1-ratio)$で割り算してあります。
ドロップアウト層には学習すべきパラメータはありませんので、実装もパスしています。
また、ドロップアウト層の追加に際して、_TypeManagerクラスにドロップアウト層を追加し、Trainerクラスの実装におけるtraining関数内の誤差計算やpredict関数で用いられているforward関数にtrain_flagを追加しておきましょう。
type_manager.pyとtrainer.py
class _TypeManager():
"""
層の種類に関するマネージャクラス
"""
N_TYPE = 5 # 層の種類数
BASE = -1
MIDDLE = 0 # 中間層のナンバリング
OUTPUT = 1 # 出力層のナンバリング
DROPOUT = 2 # ドロップアウト層のナンバリング
CONV = 3 # 畳み込み層のナンバリング
POOL = 4 # プーリング層のナンバリング
REGULATED_DIC = {"Middle": MiddleLayer,
"Output": OutputLayer,
"Dropout": Dropout,
"Conv": ConvLayer,
"Pool": PoolingLayer,
"BaseLayer": None}
@property
def reg_keys(self):
return list(self.REGULATED_DIC.keys())
def name_rule(self, name):
name = name.lower()
if "middle" in name or name == "mid" or name == "m":
name = self.reg_keys[self.MIDDLE]
elif "output" in name or name == "out" or name == "o":
name = self.reg_keys[self.OUTPUT]
elif "dropout" in name or name == "drop" or name == "d":
name = self.reg_keys[self.DROPOUT]
elif "conv" in name or name == "c":
name = self.reg_keys[self.CONV]
elif "pool" in name or name == "p":
name = self.reg_keys[self.POOL]
else:
raise UndefinedLayerError(name)
return name
import time
import matplotlib.pyplot as plt
import matplotlib.animation as animation
softmax = type(get_act("softmax"))
sigmoid = type(get_act("sigmoid"))
class Trainer(Switch):
def __init__(self, x, y, *args, mode="cpu", **kwds):
# GPU利用可能かどうか
if not mode in ["cpu", "gpu"]:
raise KeyError("'mode' must select in {}".format(["cpu", "gpu"])
+ "but you specify '{}'.".format(mode))
self.mode = mode.lower()
super().__init__(*args, mode=self.mode, **kwds)
self.x_train, self.x_test = x
self.y_train, self.y_test = y
self.x_train = self.calculator.asarray(self.x_train)
self.x_test = self.calculator.asarray(self.x_test)
self.y_train = self.calculator.asarray(self.y_train)
self.y_test = self.calculator.asarray(self.y_test)
self.make_anim = False
def forward(self, x, train_flag=True, lim_memory=10):
def propagate(x, train_flag=True):
x_in = x
n_batch = x.shape[0]
switch = True
for ll in self.layer_list:
if switch and not self.is_CNN(ll.name):
x_in = x_in.reshape(n_batch, -1)
switch = False
x_in = ll.forward(x_in, train_flag=train_flag)
# 順伝播メソッドは誤差計算や未知データの予測にも使用するため
# メモリ容量が大きくなる可能性がある
if self.calculator.prod(
self.calculator.asarray(x.shape))*8/2**20 >= lim_memory:
# 倍精度浮動小数点数(8byte)で10MB(=30*2**20)以上の
# メモリを利用する場合は5MB以下ずつに分割して実行する
n_batch = int(5*2**20/(8*self.calculator.prod(
self.calculator.asarray(x.shape[1:]))))
if self.mode == "cpu":
y = self.calculator.zeros((x.shape[0], lm[-1].n))
elif self.mode == "gpu":
y = self.calculator.zeros((x.shape[0], lm[-1].n))
n_loop = int(self.calculator.ceil(x.shape[0]/n_batch))
for i in range(n_loop):
propagate(x[i*n_batch : (i+1)*n_batch], train_flag=train_flag)
y[i*n_batch : (i+1)*n_batch] = lm[-1].y.copy()
lm[-1].y = y
else:
# そうでなければ普通に実行する
propagate(x, train_flag=train_flag)
・
・
・
def training(self, epoch, n_batch=16, threshold=1e-8,
show_error=True, show_train_error=False, **kwds):
if show_error:
self.error_list = []
if show_train_error:
self.train_error_list = []
if self.make_anim:
self.images = []
self.n_batch = n_batch
n_train = self.x_train.shape[0]//n_batch
n_test = self.x_test.shape[0]
# 学習開始
if self.mode == "gpu":
cp.cuda.Stream.null.synchronize()
start_time = time.time()
lap_time = -1
error = 0
error_prev = 0
rand_index = self.calculator.arange(self.x_train.shape[0])
for t in range(1, epoch+1):
#シーン作成
if self.make_anim:
self.make_scene(t, epoch)
# 訓練誤差計算
if show_train_error:
self.forward(self.x_train[rand_index[:n_test]],
train_flag=False)
error = lm[-1].get_error(self.y_train[rand_index[:n_test]])
self.train_error_list.append(error)
# 誤差計算
self.forward(self.x_test, train_flag=False)
error = lm[-1].get_error(self.y_test)
if show_error:
self.error_list.append(error)
・
・
・
def predict(self, x=None, y=None, threshold=0.5):
if x is None:
x = self.x_test
if y is None:
y = self.y_test
self.forward(x, train_flag=False)
self.y_pred = self.pred_func(self[-1].y, threshold=threshold)
y = self.pred_func(y, threshold=threshold)
print("correct:", y[:min(16, int(y.shape[0]*0.1))])
print("predict:", self.y_pred[:min(16, int(y.shape[0]*0.1))])
print("accuracy rate:",
100*self.calculator.sum(self.y_pred == y,
dtype=int)/y.shape[0], "%",
"({}/{})".format(self.calculator.sum(self.y_pred == y, dtype=int),
y.shape[0]))
if self.mode == "cpu":
return self.y_pred
elif self.mode == "gpu":
return self.y_pred.get()
実験
では実験してみましょう。と言っても、MNISTデータセットでの学習くらいではそれほど過学習は起こせないので効果が薄く見えるかもしれません。
実験はGoogle Colaboratory上で行っています。KerasのMNISTデータセットを利用しているためGPU利用モードで実行していますが、それでも200エポックにかかる時間は約20分です。
コードはgithubからGoogle Colaboratoryへ飛べばそのまま実行できます。
%matplotlib inline
# 畳み込み層と出力層を作成
M, F_h, F_w = 10, 3, 3
lm = LayerManager((x_train, x_test), (t_train, t_test), mode="gpu")
lm.append(name="c", I_shape=(C, I_h, I_w), F_shape=(M, F_h, F_w), pad=1)
lm.append(name="p", I_shape=lm[-1].O_shape, pool=2)
lm.append(name="m", n=100, opt="eve")
lm.append(name="d", ratio=0.5)
lm.append(name="o", n=n_class, act="softmax", err_func="Cross")
# 学習させる
epoch = 200
threshold = 1e-8
n_batch = 128
lm.training(epoch, threshold=threshold, n_batch=n_batch, show_train_error=True)
# 予測する
print("training dataset")
_ = lm.predict(x=lm.x_train, y=lm.y_train)
print("test dataset")
y_pred = lm.predict()
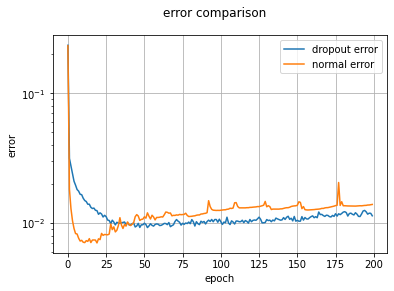
実験結果を図示するにあたり、ちょっと面倒な作業が必要になります。
まずはドロップアウト層なしの状態でテストコードのセルを実行し、別のセルに用意した下記のコードを実行します。
err_list = lm.error_list
次にドロップアウト層ありの状態でテストコードのセルを実行し、また別のセルに用意した下記のコードを実行します。
drop_error_list = lm.error_list
以上のセットアップの後、下記のコードをさらに別セルに用意して実行しましょう。
fig, ax = plt.subplots(1)
fig.suptitle("error comparison")
ax.set_xlabel("epoch")
ax.set_ylabel("error")
ax.set_yscale("log")
ax.grid()
ax.plot(drop_error_list, label="dropout error")
ax.plot(err_list, label="normal error")
ax.legend(loc="best")
これで表示できます。
比較器の実装
比較検証しやすいように比較器を実装しました。ついでに正答率も表示できるよう_Trainerクラスにshow_accuracy関数を追加したりレイヤクラスにパラメータ保持させたりなんだりしました。
import numpy as np
import matplotlib.pyplot as plt
class Comparer():
def compare(self, lm, func_dic, *args,
title="comparison result",
show_error=True, show_accuracy=True, xlabel="epoch",
error_ylabel="error",accuracy_ylabel="accuracy",
error_yscale="log", accuracy_yscale="linear", loc="best",
error_fname="", accuracy_fname="", **kwds):
if show_error:
error_list = []
if show_accuracy:
accuracy_list = []
max_len = 0
for func in func_dic.values():
# 初期化
for ll in lm.layer_list:
ll.__init__(*ll._args, **ll._kwds)
# レイヤの構造などを変化させる
func(lm)
# 学習
lm.training(*args, compare_flag=True,
show_error=show_error, show_accuracy=show_accuracy,
**kwds)
if show_error:
error_list.append(lm.error_list)
max_len = len(lm.error_list) if max_len < len(lm.error_list) \
else max_len
if show_accuracy:
accuracy_list.append(lm.accuracy_list)
max_len = len(lm.accuracy_list) \
if max_len < len(lm.accuracy_list) else max_len
if show_error:
fig, ax = plt.subplots(1)
fig.suptitle(title)
ax.set_xlabel(xlabel)
ax.set_ylabel(error_ylabel)
ax.set_yscale(error_yscale)
ax.grid()
for i, label in enumerate(func_dic):
ax.plot(np.arange(1, max_len+1), error_list[i], label=label)
ax.legend(loc=loc)
if len(error_fname) != 0:
fig.savefig(error_fname)
if show_accuracy:
fig2, ax2 = plt.subplots(1)
fig2.suptitle(title)
ax2.set_xlabel(xlabel)
ax2.set_ylabel(accuracy_ylabel)
ax2.set_yscale(accuracy_yscale)
ax2.grid()
for i, label in enumerate(func_dic):
ax2.plot(np.arange(1, max_len+1), accuracy_list[i], label=label)
ax2.legend(loc=loc)
if len(error_fname) != 0:
fig2.savefig(error_fname)
使い方は以下のような感じです。
%matplotlib inline
# 畳み込み層と出力層を作成
M, F_h, F_w = 10, 3, 3
lm = LayerManager((x_train, x_test), (t_train, t_test), mode="gpu")
lm.append(name="c", I_shape=(C, I_h, I_w), F_shape=(M, F_h, F_w), pad=1)
lm.append(name="p", I_shape=lm[-1].O_shape, pool=2)
lm.append(name="m", n=100)
lm.append(name="d", ratio=0.5)
lm.append(name="o", n=n_class, act="softmax", err_func="Cross")
# 比較方法を関数として記述したのち、lambda記法でオーバーラップする
def func(lm, ratio):
for ll in lm.layer_list:
ll._kwds["Dropout1"].ratio = ratio
func_dic = {"normal": lambda lm: func(lm, 0),
"dropout": lambda lm: func(lm, 0.5)}
# 学習させる
epoch = 100
threshold = 1e-8
n_batch = 128
comparator = Comparer()
comparator.compare(lm, func_dic, epoch, threshold=threshold, n_batch=n_batch)
比較検証する方法を関数として設定し、さらにそれを辞書型として渡します。さらに、Pythonのlambda記法でそれぞれの関数をlmだけ引数に取るようにオーバーラップします。
あとはコンパレータに引数を渡して学習・推論すればOKです。
おわりに
なんかめんどくさすぎるのでこういう比較検証を図示しやすくなるような実装を考えてみます...
P.S. 比較器を実装しました。