対象者
深層学習の最適化手法である確率的勾配降下法をまとめてみました。
といっても、こちらにまとめられている数式と論文を基に、初期値や論文に載っていなかった定数の決定などをPytorch、Keras、Chainerなどの実装を参考に行ったものをまとめただけです。
数式などは実装ライクにまとめますので、自分で実装してみたい人は見ていってください。
間違いなどがあれば気軽にご指摘ください。
また、新しい最適化手法の情報をお持ちの方や、作成中の最適化手法についても是非教えてください!
こちらで探索平面ごとの挙動の違いを紹介しています。
こちらにて実装コードを公開しています。ご自由にご活用ください。
目次
- はじめに
- 実装ベース
- SGD
- Momentum SGD
- NAG
- AdaGrad
- RMSprop
- AdaDelta
- Adam
- RMSpropGraves
- SMORMS3
- AdaMax
- Nadam
- Eve
- Santa-E
- Santa-SSS
- [GD by GD](作成中...)
- [AdaSecant](作成中...)
- AMSGrad
- AdaBound
- AMSBound
- AdaBelief
- SAM
- 実験
はじめに
まずは事前知識として最急降下法と確率的勾配降下法の違いについて説明します。と言っても大したことはありません。
最急降下法とは
最急降下法とは、ずばり損失関数を最も減少させる方向(勾配の絶対値がが最大の方向)に降下させる手法のことです。勾配降下法とも言います。
手順としては、
- 全ての入力データをニューラルネットワークに入力して計算させる
- 二乗誤差や交差エントロピー誤差などの損失関数を用いて誤差を算出
- 連鎖律を用いて各パラメータに対する損失関数の偏微分を計算する
- あるルールに則りパラメータを更新
- 損失関数の値の変化が十分小さくなるまで1〜4を繰り返す
連鎖律についてはこちらで簡単に触れています。
あるルール、というのが勾配降下法の肝です。この部分で性能が決まります。と言っても全ての問題に対して最良の勾配降下法というものは残念ながら存在しません(少なくとも現状は)。
パラメータの更新式というのは、ある時刻$t$に対して
w_{t+1} = w_t - \eta \nabla_{w_t} \mathcal{L}(w_t)
のように表すことができます。
パラメータ要素ごとに表すと
w_{t+1}^{(i)} = w_t^{(i)} - \eta \nabla_{w_{t}^{(i)}} \mathcal{L}(w_t)
などとなります(もちろんパラメータ次元は通常もっと多次元です)。
記号の説明としては
- $w_t \cdots$時刻$t$でのパラメータ
- $\eta \cdots$学習率
- $\mathcal{L}(w_t) \cdots$損失関数
です。この更新式に則るパラメータ更新を、損失関数がほとんど変化しなくなるまで繰り返します。ほとんど変化しなくなれば学習は終了したと見做します。
この時「損失関数の値が十分小さくなるまで」ではないことに注意してください。例えばパラメータが足りないなどの要因で学習が収束しない事態というのは多くの場合でありうる事態ですので、あくまで 「変化量が十分小さくなるまで」 学習を行います。
確率的勾配降下法とは
確率的勾配降下法について述べる前に、まずは最急降下法の欠点を紹介します。
最急降下法の欠点は、全ての入力データを用いてパラメータ更新を行うことにあります。
というのも、この方法では極小値に陥った際に抜け出すことができなくなります。
詳しくはこちらにあるので省略しますが、要するに一気に全データを用いて学習するとそのような状況に陥りやすくなるということです。
ちなみにですが、パラメータ次元が2次元以上になると鞍点と呼ばれるさらに厄介な点が出現します。鞍点は「あるパラメータにとっては極大値だが、別のパラメータにとっては極小値である点」のことで、これが非常に厄介です。
なぜなら、パラメータ次元が多次元になればなるほどこの鞍点というのは指数関数的に増えることが知られているからです。
これを次元の呪いとか言いますが、この鞍点は勾配が$0$であることには変わりないので学習が進みません。しかもパラメータ次元が増えると極小点や極大点よりも遥かに出現しやすくなっているため、至る所に「落とし穴」がある状況と変わりありません。
さらにさらに、パラメータ次元というのは要するに重み$w$やバイアス$b$の総数を言いますので、あっという間にとんでもない数になってしまいます。
閑話休題...
何にせよ、学習則は非常にデリケートかつ大変複雑な問題となっているということです。話題を戻します。
最急降下法の欠点は全ての入力データを用いることが原因なので、これを一つずつにしてやればとりあえず解消できそうですよね。
ということで、入力データを一つずつ使ってパラメータ更新する手法のことを確率的勾配降下法といいます。
また、このように「入力データ1つずつに対して逐次的にパラメータ更新を行う学習方法」をオンライン学習と言います。
それぞれの入力データに対して逐次的にパラメータ更新するのでより精度の良いモデルができそうですね。
ちなみにどこが確率的なのかというと、全ての入力データから一つずつデータを取り出す際にランダムに取り出しているところです。
そんな確率的勾配降下法ですが、並列化できないという欠点があります。せっかく現代はGPUなどの並列化処理が進んでるのにその恩恵を受けられないのはもったいないですよね。
そこでミニバッチ学習という手法が考案されました。発想はシンプルで、入力データを一度にある数($16$個とか$32$個らしいです)使用してパラメータを更新します。これなら並列化もできますね。
とはいえ、ミニバッチ学習を用いると 「鋭い谷では振動する」 という欠点もあったりします。この克服はもう学習則そのものに委ねるしか現状はない模様です。
実装ベース
まずは以降の実装についての基本的なことをまとめておきます。
どの最適化手法もBaseOptクラスを継承させるように実装します。
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
@dataclass
class BaseOpt():
"""Base class for optimizers.
Args:
n (int): Number of parameters to update.
eps (float): Tiny values to avoid division by zero.
"""
kind: InitVar[int] = 0
n: InitVar[int] = 2
eps: InitVar[float] = 1e-8
previous: ndarray = field(init=False, repr=False)
def __post_init__(self, kind, n, eps, *args, **kwds):
if kind:
self.previous = np.full((kind, n), eps)
else:
self.previous = None
def update(self, *args, **kwds):
raise NotImplementedError("'update' method must be implemented.")
kindはpreviousで保持したいパラメータの種類を指定します。
previousは一つ前のタイムステップの値を保持するための変数です。必要な場合は全てここに入れておきます。
nは更新対象のパラメータの数です。深層学習ではwとbの2種類のパラメータを更新する必要があるためn=2がデフォルトとなっています。
epsはゼロ除算を防ぐための微小値です。以降紹介する最適化手法にはこのepsを明示的に用いているものもあるのですが、面倒なので全て統一しています。ここで指定されたepsでpreviousを初期化することでぜろ除算を防ぐような実装になっています。
コードは以下のように一つのディレクトリにまとめて放り込んであります。
$ tree
.
├── _adabound.py
├── _adadelta.py
├── _adagrad.py
├── _adam.py
├── _adamax.py
├── _amsbound.py
├── _amsgrad.py
├── _base.py
├── _eve.py
├── _interface.py
├── _msgd.py
├── _nadam.py
├── _nag.py
├── _rmsprop.py
├── _rmsprop_graves.py
├── _sam.py
├── _sample.py
├── _sample2.py
├── _santa_e.py
├── _santa_sss.py
├── _sgd.py
├── _smorms3.py
├── optimizers.gif
└── optimizers_3d.gif
SGD
まずは最も基本的な勾配降下法です。
SGD: Stochastic Gradient Descentは日本語では確率的勾配降下法と訳されます。つまりさっき述べた学習則ですね。
数式的な表現としては最急降下法と変わりません。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
\Delta w_t &= - \eta g_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装では$g_t$は流れてくる誤差(勾配)として連鎖律によって計算されています(TensorFlowは自動微分でやってそう?)。なので$g_t$は気にしなくてOKですね。
$\Delta w_t$はこの時間ステップでの更新量です。勾配$g_t$に学習率$\eta$を乗算するだけです。
$\Delta w_t = - \eta g_t$のようにマイナスにしている理由は最後の式で足し算にするためです。それ以上の意味はないので別に$w_{t+1} = w_t - \Delta w_t$とするなら$\Delta w_t = \eta g_t$でも大丈夫です。
ハイパーパラメータの値は
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-2=10^{-2}$ |
です。
実装例
from dataclasses import dataclass
import numpy as np
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
@dataclass
class SGD(BaseOpt):
"""SGD optimizer class.
Examples:
>>> import numpy as np
>>> obj = SGD()
>>> print(obj)
SGD(eta=0.01)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.005, -0.01 ])
"""
eta: float = 1e-2
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
delta = -self.eta*grad
return delta
if __name__ == "__main__":
import doctest
doctest.testmod()
MomentumSGD
単純なSGDでは収束が遅く、また振動や鞍点に陥るなどの問題が起きやすいため改善する必要があります。
その方法の一つがモーメント(Momentum)を考慮することです。モーメントは要するに慣性ですね。一つ前の勾配の情報を用いることで振動を抑制しています。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
\Delta w_t &= \mu \Delta w_{t-1} - (1 - \mu) \eta g_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
$\eta$の掛ける場所や第二式の右辺第二項に$1-\mu$を掛けるかなどで結構表記に揺れがありますね。パッと調べただけで
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
\Delta w_t &= \mu \Delta w_{t-1} - \eta g_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
や
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
\Delta w_t &= \mu \Delta w_{t-1} - g_t \\
w_{t+1} &= w_t + \eta \Delta w_t
\end{align}
とかもありました。本記事では一番目の式で実装しています。
この辺りの表記の揺れはハイパーパラメータである$\mu$や$\eta$を適切に修正することで同等な式にできるので気にしないで大丈夫でしょう。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-2=10^{-2}$ |
| $\mu$ | mu | $0.9$ |
| $\Delta w_0$ | previous[0] -> _delta | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum
from dataclasses import dataclass, InitVar
import numpy as np
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
delta = 0
@dataclass
class MSGD(BaseOpt):
"""MSGD optimizer class.
Examples:
>>> import numpy as np
>>> obj = MSGD()
>>> print(obj)
MSGD(eta=0.01, mu=0.9)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00050001, -0.00099999])
"""
kind: InitVar[int] = 1
eta: float = 1e-2
mu: float = 0.9
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
delta = self._delta = self.mu*self._delta - (1-self.mu)*self.eta*grad
return delta
@property
def _delta(self):
return self.previous[_keys.delta]
@_delta.setter
def _delta(self, value):
self.previous[_keys.delta] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
NAG
NAG: Nesterov's Accelerated Gradient method (ネステロフの加速法)はMSGDを修正し、より収束への加速を早めた手法です。
勾配計算を一つ前の更新量を用いて行うことで1タイムステップだけ先を大雑把に見積もるようになっています。
多分ですがこの式間違ってます。
おそらく以下の数式になります。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t+\mu \Delta w_{t-1}) \\
\Delta w_t &= \mu \Delta w_{t-1} - (1-\mu)\eta g_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
他にもここでは
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t - \mu \Delta w_{t-1}) \\
\Delta w_t &= \mu \Delta w_{t-1} + (1-\mu)g_t \\
w_t &= w_{t-1} - \eta \Delta w_t
\end{align}
と書かれています(表記は本記事のものに合わせています)。やっていることは一緒ですし、実際に両方を実装して試しましたが同じような動作をしたので問題ないでしょう。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-2=10^{-2}$ |
| $\mu$ | mu | $0.9$ |
| $\Delta w_0$ | previous[0] -> _delta | $1e-8=10^{-8}$ |
としています。
実装例
from enum import IntEnum
from typing import Any
from dataclasses import dataclass, InitVar
import numpy as np
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
#from ..layer._base import BaseLayer
class _keys(IntEnum):
delta = 0
@dataclass
class NAG(BaseOpt):
"""NAG optimizer class.
Examples:
#>>> import numpy as np
#>>> obj = NAG()
#>>> print(obj)
#NAG(delta=array([1.e-08, 1.e-08]), eta=0.01, mu=0.9)
#>>> obj.update(np.array([-0.5, 1]))
#array([ 0.00050001, -0.00099999])
"""
kind: InitVar[int] = 1
parent: Any = None #: BaseLayer = None
eta: float = 1e-2
mu: float = 0.9
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
self.delta (ndarray): Update delta.
"""
# Repropagation.
self.parent.params += self.mu*self._delta
_ = self.parent.forward(self.parent.x)
grad = self.parent.backward(self.parent.grad)
self.parent.params -= self.mu*self._delta
# Compute update delta.
delta = self._delta = self.mu*self._delta - (1-self.mu)*self.eta*grad
return delta
@property
def _delta(self):
return self.previous[_keys.delta]
@_delta.setter
def _delta(self, value):
self.previous[_keys.delta] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
せっかく連鎖律で流れてきた勾配を改めて流し直す必要があるので深層学習では使いづらそうですね...というかどうやるんだろうか...
AdaGrad
MSGDでは収束方向に関する情報を用いていなかったため、緩やかな勾配の方向には収束が遅いという問題があります。
これを解消するための、学習率を各次元ごとに調整する手法のパイオニアがAdaGradです。
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L}(w_t) \\
\Delta w_t &= - \cfrac{\eta}{\displaystyle\sqrt{\sum_{\tau=1}^{t}{g_{\tau}^2}}} g_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装上では第二式の二乗和を
\begin{align}
gw_t = gw_{t-1} + g_t^2
\end{align}
のようにして保持することでメモリと計算量を節約しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-3=10^{-3}$ |
| $gw_0$ | previous[0] -> _sum_g | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum
from dataclasses import dataclass, InitVar
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
sum_g = 0
@dataclass
class AdaGrad(BaseOpt):
"""AdaGrad optimizer class.
Examples:
>>> import numpy as np
>>> obj = AdaGrad()
>>> print(obj)
AdaGrad(eta=0.001)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.001, -0.001])
"""
kind: InitVar[int] = 1
eta: float = 1e-3
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
self._sum_g += grad*grad
delta = -grad*self.eta/np.sqrt(self._sum_g)
return delta
@property
def _sum_g(self):
return self.previous[_keys.sum_g]
@_sum_g.setter
def _sum_g(self, value):
self.previous[_keys.sum_g] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
RMSprop
AdaGradでは急勾配のあと緩やかな勾配があり、その後また谷がある場合でも谷にあまり降りていきません。
その理由は勾配の二乗が蓄積され続け、学習率が小さくなり続けるためです。
これを改善したのがRMSpropです。勾配の影響を係数$\rho$で「忘れていく」ことで、学習率が下がり続けるという問題を解決しています。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
v_t &= \rho v_{t-1} + (1-\rho)g_t^2 \\
\Delta w_t &= - \cfrac{\eta}{\sqrt{v_t + \varepsilon}}g_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して、第二式を
\begin{align}
v_t &= \rho v_{t-1} + (1-\rho)g_t^2 \\
\Leftrightarrow
v_t &= (v_{t-1} - v_{t-1}) + \rho v_{t-1} + (1-\rho)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} - (1-\rho)v_{t-1} + (1-\rho)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\rho)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-2=10^{-2}$ |
| $\rho$ | rho | $0.99$ |
| $v_0$ | previous[0] -> _v | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum
from dataclasses import dataclass, InitVar
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
v = 0
@dataclass
class RMSprop(BaseOpt):
"""RMSprop optimizer class.
Examples:
>>> import numpy as np
>>> obj = RMSprop()
>>> print(obj)
RMSprop(eta=0.01, rho=0.99)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.0999998 , -0.09999995])
"""
kind: InitVar[int] = 1
eta: float = 1e-2
rho: float = 0.99
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
self._v += (1-self.rho)*(grad*grad - self._v)
delta = -grad*self.eta/np.sqrt(self._v)
return delta
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
AdaDelta
RMSpropは実は物理的に間違っています。簡単に言うと両辺の次元が一致していません。
物理の問題を解いているわけではないのでそれほど問題にならない...と言いたいですが、これには少し問題があります。
と言うのも、ハイパーパラメータである$\eta$を各問題に対してフィッティングする必要があります。例えば
\begin{align}
f(x) &= x^2 \\
g(x) &= 10x^2
\end{align}
という二つの関数をそれぞれフィッティングすることを考えます。この時、次元が一致していない学習則を用いると学習率をそれぞれの関数に対して調整する必要が出てきます。つまりハイパーパラメータを調整する必要があるわけですね。
これがめんどくさい上に大変な作業で、もし1回学習するのに数日かかるような大規模な学習を行う際にこれを行うとなると、一体どれほどの時間を無駄にするのか想像もつきませんね。
ということで次元の不一致というのは結構な問題で、それを解決するのがこのAdaDeltaというわけです。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
v_t &= \rho v_{t-1} + (1-\rho) g_t^2 \\
\Delta w_t &= - \cfrac{\sqrt{u_{t-1} + \varepsilon}}{\sqrt{v_t + \varepsilon}} g_t \\
u_t &= \rho u_{t-1} + (1-\rho) (\Delta w_t)^2 \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して第二式および第四式を
\begin{align}
v_t &= \rho v_{t-1} + (1-\rho)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\rho)(g_t^2 - v_{t-1}) \\
u_t &= \rho u_{t-1} + (1-\rho) (\Delta w_t)^2 \\
\Leftrightarrow
u_t &= u_{t-1} + (1-\rho) \left\{ ( \Delta w_t)^2 - u_{t-1} \right\}
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\rho$ | rho | $0.95$ |
| $v_0$ | previous[0] -> _v | $1e-8=10^{-8}$ |
| $u_0$ | previous[1] -> _u | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
v = 0
u = auto()
@dataclass
class AdaDelta(BaseOpt):
"""AdaDelta optimizer class.
Examples:
>>> import numpy as np
>>> obj = AdaDelta()
>>> print(obj)
AdaDelta(rho=0.95)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00447197, -0.00447209])
"""
kind: InitVar[int] = 2
rho: float = 0.95
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
self._v += (1-self.rho)*(grad*grad - self._v)
delta = -grad*np.sqrt(self._u)/np.sqrt(self._v)
self._u += (1-self.rho)*(delta*delta - self._u)
return delta
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
@property
def _u(self):
return self.previous[_keys.u]
@_u.setter
def _u(self, value):
self.previous[_keys.u] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
Adam
言わずと知れた有名なアルゴリズムAdamです。以降様々な改良がなされていますがいまだに現役バリバリのようです。なんと言ってもやはり汎用性が高いのが強みですね〜
しかし、RMSpropを改良したものには違いがないので、実は次元が一致していないという問題もあります。
それでも他の学習則と比べると、勾配情報も忘れていくという特性から次元の問題が軽減されていると考えられています。
2020/12/24修正
$\alpha_t$の分母が$1-\beta_1^2$になっていたので$1-\beta_1^t$に修正しました。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
m_t &= \beta_1 m_{t-1} + (1- \beta_1) g_t \\
v_t &= \beta_2 v_{t-1} + (1- \beta_2) g_t^2 \\
\alpha_t &= \alpha_0 \cfrac{\sqrt{1-\beta_2^t}}{1- \beta_1^t} \\
\Delta w_t &= - \alpha_t \cfrac{m_t}{\sqrt{v_t + \varepsilon}} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
上記の式は元論文の文中に載っている改良コードを使用しています。そのままの数式だと
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
m_t &= \beta_1 m_{t-1} + (1- \beta_1) g_t \\
v_t &= \beta_2 v_{t-1} + (1- \beta_2) g_t^2 \\
\hat{m}_t &= \cfrac{m_t}{1-\beta_1^t} \\
\hat{v}_t &= \cfrac{v_t}{1-\beta_2^t} \\
\Delta w_t &= - \alpha_0 \cfrac{\hat{m}_t}{\sqrt{\hat{v}_t + \varepsilon}} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
ですね。
実装に際して第二式および第三式を
\begin{align}
m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\beta_1)(g_t - m_{t-1}) \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\beta_2)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha_0$ | alpha | $1e-3=10^{-3}$ |
| $\beta_1$ | beta1 | $0.9$ |
| $\beta_2$ | beta2 | $0.999$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previous[1] -> _v | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
v = auto()
@dataclass
class Adam(BaseOpt):
"""Adam optimizer class.
Examples:
>>> import numpy as np
>>> obj = Adam()
>>> print(obj)
Adam(alpha=0.001, beta1=0.9, beta2=0.999)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00099998, -0.001 ])
"""
kind: InitVar[int] = 2
alpha: float = 1e-3
beta1: float = 0.9
beta2: float = 0.999
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.beta1)*(grad-self._m)
self._v += (1-self.beta2)*(grad*grad - self._v)
alpha_t = self.alpha*np.sqrt(1 - self.beta2**t)/(1 - self.beta1**t)
delta = -alpha_t*self._m/np.sqrt(self._v)
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
RSMpropGraves
こちらはGraves氏が考案したRMSpropの改良版です。手書き文字認識の分野で用いられているそうです。
\begin{align}
g_t &= \nabla_{w_t} (w_t) \\
m_t &= \rho m_{t-1} + (1-\rho) g_t \\
v_t &= \rho v_{t-1} + (1-\rho) g_t^2 \\
\Delta w_t &= - \eta \cfrac{g_t}{\sqrt{v_t - m_t^2 + \varepsilon}} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して第二式および第三式を
\begin{align}
m_t &= \rho m_{t-1} + (1-\rho)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\rho)(g_t - m_{t-1}) \\
v_t &= \rho v_{t-1} + (1-\rho)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\rho)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-4=10^{-4}$ |
| $\rho$ | rho | $0.95$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previous[1] -> _v | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
v = auto()
@dataclass
class RMSpropGraves(BaseOpt):
"""RMSpropGraves optimizer class.
Examples:
>>> import numpy as np
>>> obj = RMSpropGraves()
>>> print(obj)
RMSpropGraves(eta=0.0001, rho=0.95)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00045692, -0.00045842])
"""
kind: InitVar[int] = 2
eta: float = 1e-4
rho: float = 0.95
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.rho)*(grad-self._m)
self._v += (1-self.rho)*(grad*grad - self._v)
delta = -grad*self.eta/np.sqrt(self._v - self._m*self._m)
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
SMORMS3
さらにこちらもRMSpropの改良ですね。次元の問題を曲率とLeCun法で克服したものらしいです。LeCun法がなんなのかはよくわかりませんが、LeCun氏は誤差逆伝播法におけるテクニックを提唱したり、LeNetなるモデルを発表したりしているみたいですね。
**2020/6/15修正**
[元論文](https://sifter.org/~simon/journal/20150420.html)と異なる点がありましたので修正します。\begin{align}
s_t &= 1 + (1-\zeta_{t-1}s_{t-1}) \\
\rho_t &= \cfrac{1}{s_t + 1}
\end{align}
\begin{align}
\rho_t &= \cfrac{1}{s_{t-1} + 1} \\
& \vdots \\
s_t &= 1 + (1-\zeta_{t-1})s_{t-1}
\end{align}
\begin{align}
g_t &= \nabla_{w_t}(w_t) \\
\rho_t &= \cfrac{1}{s_{t-1} + 1} \\
s_t &= 1 + (1-\zeta_{t-1})s_{t-1} \\
m_t &= \rho_t m_{t-1} + (1-\rho_t) g_t \\
v_t &= \rho_t v_{t-1} + (1-\rho_t) g_t^2 \\
\zeta_t &= \cfrac{m_t^2}{v_t + \varepsilon} \\
\Delta w_t &= -\cfrac{\textrm{min}\{ \eta, \zeta_t \}}{\sqrt{v_t + \varepsilon}} g_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して第四式および第五式を
\begin{align}
m_t &= \rho_t m_{t-1} + (1-\rho_t)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\rho_t)(g_t - m_{t-1}) \\
v_t &= \rho_t v_{t-1} + (1-\rho_t)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\rho_t)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-3=10^{-3}$ |
| $s_t$ | previous[0] -> _s | $1$ |
| $m_0$ | previous[1] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previous[2] -> _v | $1e-8=10^{-8}$ |
| $\zeta_0$ | previous[3] -> _zeta | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
s = 0
m = auto()
v = auto()
zeta = auto()
@dataclass
class SMORMS3(BaseOpt):
"""SMORMS3 optimizer class.
Examples:
>>> import numpy as np
>>> obj = SMORMS3()
>>> print(obj)
SMORMS3(eta=0.001)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00141421, -0.00141421])
"""
kind: InitVar[int] = 4
eta: float = 1e-3
def __post_init__(self, *args, **kwds):
super().__post_init__(*args, **kwds)
self.previous[_keys.s] = 1
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
rho = 1/(1+self._s)
self._s += 1 - self._zeta*self._s
self._m += (1-rho)*(grad - self._m)
self._v += (1-rho)*(grad*grad - self._v)
self._zeta = (self._m*self._m/self._v)
delta = -grad*np.minimum(self.eta, self._zeta)/np.sqrt(self._v)
return delta
@property
def _s(self):
return self.previous[_keys.s]
@_s.setter
def _s(self, value):
self.previous[_keys.s] = value
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
@property
def _zeta(self):
return self.previous[_keys.zeta]
@_zeta.setter
def _zeta(self, value):
self.previous[_keys.zeta] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
AdaMax
Adamの無次元化バージョンです。
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L} (w_t) \\
m_t &= \beta_1 m_{t-1} + (1-\beta_1) g_t \\
u_t &= \textrm{max}\left\{ \beta_2 u_{t-1}, |g_t| \right\} \\
\Delta w_t &= - \cfrac{\alpha}{1-\beta_1^t}\cfrac{m_t}{u_t} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して第二式を
\begin{align}
m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\beta_1)(g_t - m_{t-1}) \end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha$ | alpha | $2e-3=2 \times 10^{-3}$ |
| $\beta_1$ | beta1 | $0.9$ |
| $\beta_2$ | beta2 | $0.999$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $u_0$ | previous[1] -> _u | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
u = auto()
@dataclass
class AdaMax(BaseOpt):
"""AdaMax optimizer class.
Examples:
>>> import numpy as np
>>> obj = AdaMax()
>>> print(obj)
AdaMax(alpha=0.002, beta1=0.9, beta2=0.999)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.002, -0.002])
"""
kind: InitVar[int] = 2
alpha: float = 2e-3
beta1: float = 0.9
beta2: float = 0.999
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.beta1)*(grad-self._m)
self._u = np.maximum(self.beta2*self._u, np.abs(grad))
alpha_t = self.alpha/(1 - self.beta1**t)
delta = -alpha_t*self._m/self._u
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _u(self):
return self.previous[_keys.u]
@_u.setter
def _u(self, value):
self.previous[_keys.u] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
Nadam
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L} (w_t) \\
m_t &= \mu m_{t-1} + (1-\mu) g_t \\
v_t &= \nu v_{t-1} + (1-\nu) g_t^2 \\
\hat{m}_t &= \cfrac{\mu}{1 - \mu^{t+1}} m_t + \cfrac{1-\mu}{1-\mu^t} g_t \\
\hat{v}_t &= \cfrac{\nu}{1-\nu^t} v_t \\
\Delta w_t &= - \alpha \cfrac{\hat{m}_t}{\sqrt{\hat{v}_t + \varepsilon}} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実は$\alpha$と$\mu$はタイムステップに依存したパラメータで、本当ならば
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L} (w_t) \\
m_t &= \mu_t m_{t-1} + (1-\mu_t) g_t \\
v_t &= \nu v_{t-1} + (1-\nu) g_t^2 \\
\hat{m}_t &= \cfrac{\mu_t}{1 - \displaystyle\prod_{\tau=1}^{t+1}{\mu_{\tau}}} m_t + \cfrac{1-\mu_t}{1-\displaystyle\prod_{\tau=1}^{t}{\mu_{\tau}}} g_t \\
\hat{v}_t &= \cfrac{\nu}{1-\nu^t} v_t \\
\Delta w_t &= - \alpha_t \cfrac{\hat{m}_t}{\sqrt{\hat{v}_t + \varepsilon}} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
という数式で表現されます。しかし大抵の場合固定されているらしいのでとりあえず固定して実装しました。
実装に際して第二式および第三式を
\begin{align}
m_t &= \mu m_{t-1} + (1-\mu)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\mu)(g_t - m_{t-1}) \\
v_t &= \nu v_{t-1} + (1-\nu)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\nu)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha$ | alpha | $2e-3=2 \times 10^{-3}$ |
| $\mu$ | mu | $0.975$ |
| $\nu$ | nu | $0.999$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previous[1] -> _v | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
v = auto()
@dataclass
class Nadam(BaseOpt):
"""Nadam optimizer class.
Examples:
>>> import numpy as np
>>> obj = Nadam()
>>> print(obj)
Nadam(alpha=0.002, mu=0.975, nu=0.999)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00298878, -0.00298882])
"""
kind: InitVar[int] = 2
alpha: float = 2e-3
mu: float = 0.975
nu: float = 0.999
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.mu)*(grad - self._m)
self._v += (1-self.nu)*(grad*grad - self._v)
m_hat = (self._m*self.mu/(1 - self.mu**(t+1))
+ grad*(1-self.mu)/(1 - self.mu**t))
v_hat = self._v*self.nu/(1 - self.nu**t)
delta = -self.alpha*m_hat/np.sqrt(v_hat)
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
Eve
Adamの改良版ですね。フラットエリア(勾配がほぼゼロの領域)での学習を高速化しています。
いちいち名前がお洒落ですよね〜アダムとイブって
2020/12/25修正
目的関数$f$の初期値設定が元論文中にもないのでもしかしたら間違っているかもしれませんが、$t=1$の時に$f_t = f_{t-1}$としました。
2020/12/28修正
全てのtについて更新式がないことに気づいたのでさらに変更。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
m_t &= \beta_1 m_{t-1} + (1-\beta_1) g_t \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\
\hat{m}_t &= \cfrac{m_t}{1-\beta_1^t} \\
\hat{v}_t &= \cfrac{v_t}{1-\beta_2^t} \\
\textrm{if} \quad &t \gt 1 \\
& d_t = \cfrac{\left| f_t - f_{t-1} \right|}{\textrm{min} \left\{ f_t, f_{t-1} \right\} - f^{\star}} \\
& \hat{d}_t = \textrm{clip}\left( d_t, \left[ \frac{1}{c}, c \right] \right) \\
& \tilde{d}_t = \beta_3 \tilde{d}_{t-1} + (1-\beta_3)\hat{d}_t \\
\textrm{else} \\
& \tilde{d}_t = 1 \\
\textrm{end} &\textrm{if} \\
f_t &= f_{t-1} \\
\Delta w_t &= - \cfrac{\alpha}{\tilde{d}_t} \cfrac{\hat{m}_t}{\sqrt{\hat{v}_t} + \varepsilon} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
大変すぎる...数式中の記号についていくつか補足しておきます。
$f_t$はタイムステップ$t$での目的関数$f$の値になります。
$f^{\star}$は目的関数の最小値です。が、元論文によると損失関数に二乗誤差や交差エントロピー誤差を用いると$0$で良いそうです。
$\textrm{clip}$は最小値と最大値を設定して、それを下回る/上回る値を設定値に丸め込む関数です。
実装に際して第二式および第三式を
\begin{align}
m_t &= \mu m_{t-1} + (1-\mu)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\mu)(g_t - m_{t-1}) \\
v_t &= \nu v_{t-1} + (1-\nu)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\nu)(g_t^2 - v_{t-1}) \\
\tilde{d}_t &= \beta_3 \tilde{d}_{t-1} + (1-\beta_3)\hat{d}_t \\
\Leftrightarrow
\tilde{d}_t &= \tilde{d}_{t-1} + (1-\beta_3)(\hat{d}_t-\tilde{d}_{t-1})
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha$ | alpha | $1e-3=10^{-3}$ |
| $\beta_1$ | beta1 | $0.9$ |
| $\beta_2$ | beta2 | $0.999$ |
| $\beta_3$ | beta3 | $0.999$ |
| $c$ | c | $10$ |
| $f^{\star}$ | fstar | $0$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previous[1] -> _v | $1e-8=10^{-8}$ |
| $f_t$ | previous[2] -> _f | $1e-8=10^{-8}$ |
| $\tilde{d}_0$ | previous[3] -> _d_tilde | $1e-8=10^{-8}$ |
となっています。
実装例
from typing import Union
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
v = auto()
f = auto()
d_tilde = auto()
@dataclass
class Eve(BaseOpt):
"""Eve optimizer class.
Examples:
>>> import numpy as np
>>> obj = Eve()
>>> print(obj)
Eve(alpha=0.001, beta1=0.9, beta2=0.999, beta3=0.999, c=10, f_star=0)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00099998, -0.001 ])
"""
kind: InitVar[int] = 4
alpha: float = 1e-3
beta1: float = 0.9
beta2: float = 0.999
beta3: float = 0.999
c: float = 10
f_star: Union[float, ndarray] = 0
def update(self, grad, *args, t=1, f=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
f (float): Current objective value.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.beta1)*(grad-self._m)
self._v += (1-self.beta2)*(grad*grad - self._v)
m_hat = self._m/(1 - self.beta1**t)
v_hat = self._v/(1 - self.beta2**t)
if t > 1:
d = (np.abs(self._f-self.f_star)
/(np.minimum(self._f, f)-self.f_star))
d_hat = np.clip(d, 1/self.c, self.c)
self._d_tilde += (1-self.beta3)*(d_hat-self._d_tilde)
else:
self._d_tilde = 1
self._f = f
delta = -self.alpha/self._d_tilde*m_hat/np.sqrt(v_hat)
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
@property
def _f(self):
return self.previous[_keys.f]
@_f.setter
def _f(self, value):
self.previous[_keys.f] = value
@property
def _d_tilde(self):
return self.previous[_keys.d_tilde]
@_d_tilde.setter
def _d_tilde(self, value):
self.previous[_keys.d_tilde] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
Santa-E
AdamやRMSpropにマルコフ連鎖モンテカルロ法(MCMC)を取り入れたものです。その中でもSanta-EはEuler型を用いているらしい?
元論文は実装に際して流し読みしましたが、正直さっぱりわかりません...笑
しかしわからなくても数式通り設計すればコードは書ける!ということで頑張りました。というか元論文初期値とか与えてくれてなくて困ったものです...PytorchやKeras、Chainerなどの実装を覗き見させていただいて(全部バラバラでした...)、自分が実装する上で必要だと感じたハイパーパラメータのみ使用しています。
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L}(w_t) \\
v_t &= \sigma v_{t-1} + \cfrac{1-\sigma}{N^2} g_t^2 \\
\mathcal{G}_t &= \cfrac{1}{\sqrt{\lambda + \sqrt{v_t}}} \\
\textrm{if} \quad &t \lt burnin \\
& \alpha_t = \alpha_{t-1} + (u_t^2 - \cfrac{\eta}{\beta_t}) \\
& u_t = \cfrac{\eta}{\beta_t}\cfrac{1-\frac{\mathcal{G}_{t-1}}{\mathcal{G}_t}}{u_{t-1}} + \sqrt{\cfrac{2\eta}{\beta_t}\mathcal{G}_{t-1}} \otimes \zeta_t \\
\textrm{else} \\
& \alpha_t = \alpha_{t-1} \\
& u_t = 0 \\
\textrm{end} &\textrm{if} \\
u_t &= u_t + (1-\alpha_t) \otimes u_{t-1} - \eta \mathcal{G}_t \otimes g_t \\
\Delta w_t &= \mathcal{G}_t \otimes u_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
要素積$\otimes$がたくさん出てきてますが気にしなくてOKです。普通に実装する際に気をつけるべきは行列積の方ですし。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-2=10^{-2}$ |
| $\sigma$ | sigma | $0.95$ |
| $\beta_t$ | anne_func, anne_rate | t^{rate}, 0.5 |
| $burnin$ | burnin | $100$ |
| $C$ | C | $5$ |
| $N$ | N | 16 |
| $\zeta_t$ | 変数に格納せず直接乱数を生成 | $\mathcal{N} (0, 1)$ |
| $\alpha$ | previous[0] -> _alpha | $\sqrt{\eta}C$ |
| $u_0$ | previous[1] -> _u | $\sqrt{\eta} \mathcal{N} (0, 1)$ |
| $v_0$ | previous[2] -> _v | $1e-8=10^{-8}$ |
| $\mathcal{G}_t$ | previous[3] -> _g | $1e-8=10^{-8}$ |
となっています。
$\mathcal{N}(0, 1)$は標準正規分布に則る乱数です。
また、$\beta$はコード中のanne_funcとanne_rateで決定されます。元論文には特にこれと言った指定はありませんが、条件として$t \to \infty$で$\beta_t \to \infty$となる必要があります。見たところKeras、Pytorch、Chainerと言った有名機械学習ライブラリでは$\beta_t = \sqrt{t}$で計算していました。
しかし別に条件を満たせばなんでも良いっぽい?現に論文にも$\beta_t = t^2$での実験も載っていますし。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
from typing import Callable
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
alpha = 0
u = auto()
v = auto()
g = auto()
@dataclass
class SantaE(BaseOpt):
"""SantaE optimizer class.
Examples:
>>> import numpy as np
>>> obj = SantaE()
>>> print(obj)
SantaE(eta=0.01, sigma=0.95, anne_rate=0.5, burnin=100, C=5, N=16)
"""
kind: InitVar[int] = 4
eta: float = 1e-2
sigma:float = 0.95
#lambda_: float = 1e-8
anne_func: Callable = field(default=lambda t, rate: t**rate, repr=False)
anne_rate: float = 0.5
burnin: int = 100
C: int = 5
N: int = 16
def __post_init__(self, *args, **kwds):
super().__post_init__(*args, **kwds)
self.previous[_keys.alpha] = np.sqrt(self.eta)*self.C
self.previous[_keys.u] \
= (np.sqrt(self.eta)
*np.random.randn(*self.previous[_keys.u].shape))
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._v += (1-self.sigma)*(grad * grad / self.N**2 - self._v)
#g_t = 1/np.sqrt(self.lambda_+np.sqrt(self._v))
g_t = 1/np.sqrt(np.sqrt(self._v))
eta_div_beta = self.eta/self.anne_func(t, self.anne_rate)
if t < self.burnin:
self._alpha += self._u*self._u - eta_div_beta
u_t = eta_div_beta*(1 - self._g/g_t)/self._u
u_t += (np.sqrt(2*eta_div_beta*self._g)
*np.random.randn(*self._u.shape))
else:
u_t = 0
self._g = g_t
self._u += u_t - self._alpha*self._u - self.eta*self._g*grad
delta = self._g*self._u
return delta
@property
def _alpha(self):
return self.previous[_keys.alpha]
@_alpha.setter
def _alpha(self, value):
self.previous[_keys.alpha] = value
@property
def _u(self):
return self.previous[_keys.u]
@_u.setter
def _u(self, value):
self.previous[_keys.u] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
@property
def _g(self):
return self.previous[_keys.g]
@_g.setter
def _g(self, value):
self.previous[_keys.g] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
Santa-SSS
こちらも同じ論文に記載されているアルゴリズムですね。全く理解できませんが実装はできます。リーマン情報幾何学とはなんぞや...
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L}(w_t) \\
v_t &= \sigma v_{t-1} + \cfrac{1-\sigma}{N^2} g_t^2 \\
\mathcal{G}_t &= \cfrac{1}{\sqrt{\lambda + \sqrt{v_t}}} \\
\Delta w_t &= \mathcal{G}_t \otimes u_{t-1} \times 0.5 \\
\textrm{if} \quad &t \lt burnin \\
& \alpha_t = \alpha_{t-1} + (u_{t-1}^2 - \cfrac{\eta}{\beta_t}) \times 0.5 \\
& u_t = e^{- 0.5\alpha_t} \otimes u_{t-1} \\
& u_t = u_t - \mathcal{G}_t \otimes g_t \eta + \sqrt{2\mathcal{G}_{t-1} \cfrac{\eta}{\beta_t}} \otimes \zeta_t + \cfrac{\eta}{\beta_t}\cfrac{
1 - \frac{\mathcal{G}_{t-1}}{\mathcal{G}_t}}{u_{t-1}} \\
& u_t = e^{-0.5\alpha_t} \otimes u_t \\
& \alpha_t = \alpha_t + \left( u_t^2 - \cfrac{\eta}{\beta_t} \right) \times 0.5 \\
\textrm{else} \\
& \alpha_t = \alpha_{t-1} \\
& u_t = e^{-0.5\alpha_t} \otimes u_{t-1} \\
& u_t = u_t - \mathcal{G}_t \otimes g_t \eta \\
& u_t = e^{-0.5\alpha_t} \otimes u_t \\
\textrm{end} &\textrm{if} \\
\Delta w_t &= \Delta w_t + \mathcal{G}_t \otimes u_t \times 0.5 \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\eta$ | eta | $1e-2=10^{-2}$ |
| $\sigma$ | sigma | $0.95$ |
| $\beta_t$ | anne_func, anne_rate | t^{rate}, 0.5 |
| $burnin$ | burnin | $100$ |
| $C$ | C | $5$ |
| $N$ | N | 16 |
| $\zeta_t$ | 変数に格納せず直接乱数を生成 | $\mathcal{N} (0, 1)$ |
| $\alpha_t$ | previous[0] -> _alpha | $\sqrt{\eta}C$ |
| $u_0$ | previous[1] -> _u | $\sqrt{\eta} \mathcal{N} (0, 1)$ |
| $v_0$ | previous[2] -> _v | $1e-8=10^{-8}$ |
| $\mathcal{G}_t$ | previous[3] -> _g | $1e-8=10^{-8}$ |
| $\Delta w_t$ | previous[4] -> _delta | $\sqrt{\eta} \mathcal{N} (0, 1)$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
from typing import Callable
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
alpha = 0
u = auto()
v = auto()
g = auto()
delta = auto()
@dataclass
class SantaSSS(BaseOpt):
"""SantaSSS optimizer class.
Examples:
>>> import numpy as np
>>> obj = SantaSSS()
>>> print(obj)
SantaSSS(eta=0.01, sigma=0.95, anne_rate=0.5, burnin=100, C=5, N=16)
"""
kind: InitVar[int] = 5
eta: float = 1e-1
sigma:float = 0.95
#lambda_: float = 1e-8
anne_func: Callable = field(default=lambda t, rate: t**rate, repr=False)
anne_rate: float = 0.5
burnin: int = 100
C: int = 5
N: int = 16
def __post_init__(self, *args, **kwds):
super().__post_init__(*args, **kwds)
self._alpha = np.sqrt(self.eta)*self.C
self.previous[[_keys.u, _keys.delta]] \
= (np.sqrt(self.eta)
*np.random.randn(
*self.previous[[_keys.u, _keys.delta]].shape))
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._v += (1-self.sigma)*(grad * grad / self.N**2 - self._v)
#g_t = 1/np.sqrt(self.lambda_+np.sqrt(self._v))
g_t = 1/np.sqrt(np.sqrt(self._v))
self._delta = 0.5*g_t*self._u
eta_div_beta = self.eta/self.anne_func(t, self.anne_rate)
if t < self.burnin:
self._alpha += 0.5*(self._u*self._u - eta_div_beta)
u_t = np.exp(-0.5*self._alpha)*self._u
u_t -= self.eta*g_t*grad
u_t += (np.sqrt(2*eta_div_beta*self._g)
* np.random.randn(*self._u.shape))
u_t += eta_div_beta*(1 - self._g/g_t)/self._u
self._u = np.exp(-0.5*self._alpha)*u_t
self._alpha += 0.5*(self._u*self._u - eta_div_beta)
else:
self._u *= np.exp(-0.5*self._alpha)
self._u -= self.eta*g_t*grad
self._u *= np.exp(-0.5*self._alpha)
self._g = g_t
self._delta += 0.5*self._g*self._u
delta = self._delta
return delta
@property
def _alpha(self):
return self.previous[_keys.alpha]
@_alpha.setter
def _alpha(self, value):
self.previous[_keys.alpha] = value
@property
def _u(self):
return self.previous[_keys.u]
@_u.setter
def _u(self, value):
self.previous[_keys.u] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
@property
def _g(self):
return self.previous[_keys.g]
@_g.setter
def _g(self, value):
self.previous[_keys.g] = value
@property
def _delta(self):
return self.previous[_keys.delta]
@_delta.setter
def _delta(self, value):
self.previous[_keys.delta] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
GD by GD
論文読みます...さっぱりわからないけど...
AdaSecant
論文読みます...移動平均関係がわからない...
AMSGrad
RMSprop、AdaDelta、Adam、Nadamでは指数移動平均によって指数減衰が行われていましたが、これのせいで例え重要な勾配情報が流れてきてもすぐに忘れてしまうため最適解に収束できないことがあります。
その問題を解決したのがAMSGradです。
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L} (w_t) \\
m_t &= \beta_1 m_{t-1} + (1-\beta_1) g_t \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\
\hat{v}_t &= \textrm{max}\{ \hat{v}_{t-1}, v_t \} \\
\Delta w_t &= - \alpha_t \cfrac{m_t}{\sqrt{\hat{v}_t + \varepsilon}} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して第二式および第三式を
\begin{align}
m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\beta_1)(g_t - m_{t-1}) \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\beta_2)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。また$\alpha_t=\frac{\alpha}{\sqrt{t}}$で計算すると良いっぽい?論文中にそれっぽい記述がありました。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha_0$ | alpha | $1e-3=10^{-3}$ |
| $\beta_1$ | beta1 | $0.9$ |
| $\beta_2$ | beta2 | $0.999$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previous[1] -> _v | $1e-8=10^{-8}$ |
| $\hat{v}_0$ | previous[2] -> _v_hat | $1e-8=10^{-8}$ |
となっています。初期値$\alpha_0$に関しては論文中に具体的な値は載っていなかったのでChainerより持ってきました。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
v = auto()
v_hat = auto()
@dataclass
class AMSGrad(BaseOpt):
"""AMSGrad optimizer class.
Examples:
>>> import numpy as np
>>> obj = AMSGrad()
>>> print(obj)
AMSGrad(alpha=0.001, beta1=0.9, beta2=0.999)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00316221, -0.00316226])
"""
kind: InitVar[int] = 3
alpha: float = 1e-3
beta1: float = 0.9
beta2: float = 0.999
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.beta1)*(grad-self._m)
self._v += (1-self.beta2)*(grad*grad - self._v)
self._v_hat = np.maximum(self._v_hat, self._v)
delta = -self.alpha*self._m/np.sqrt(self._v_hat)
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
@property
def _v_hat(self):
return self.previous[_keys.v_hat]
@_v_hat.setter
def _v_hat(self, value):
self.previous[_keys.v_hat] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
AdaBound
AMSGradは学習率が不要に大きくなる問題を抑えましたが、逆の不要に小さくなる問題は解決していませんでした。
AdaBoundとAMSBoundはAdamの「学習が早いが汎化誤差をうまく抑えられない」点と、SGDの「最終的な汎化誤差は小さくできるがそれまでが遅い」点を組み合わせ、序盤はAdam、終盤はSGDのように振る舞う最適化手法として提案されました。
AdaBoundはAdamを改良したものになります。
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L} (w_t) \\
m_t &= \beta_1 m_{t-1} + (1-\beta_1) g_t \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\
\hat{\eta}_t &= \textrm{clip}\left( \cfrac{\alpha}{\sqrt{v_t}}, \left[ \eta_l(t), \eta_h(t) \right] \right) \\
\eta_t &= \cfrac{\hat{\eta}_t}{\sqrt{t}} \\
\Delta w_t &= - \eta_t m_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して第二式および第三式を
\begin{align}
m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\beta_1)(g_t - m_{t-1}) \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\beta_2)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。
またSGDとしての学習率(終盤の学習率)を$\eta$とすると、
\begin{align}
\eta_l(t) &= \eta \left( 1 - \cfrac{1}{(1-\beta_2)t+1} \right) \\
\eta_u(t) &= \eta \left( 1 + \cfrac{1}{(1-\beta_2)t} \right)
\end{align}
と論文中では計算しているようですので(多分)それを採用します。
2020/12/28修正
$eta_u(t)$の式、符号を間違えていました。
実際には、
- $\eta_l$は$t=0$では$0$、$t \to \infty$では$\eta_-$
- $\eta_u$は$t=0$では$\infty$、$t \to \infty$では$\eta_+$
- $\eta_{\pm}$はそれぞれ右極限、左極限
となれば良いようです。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha_0$ | alpha | $1e-3=10^{-3}$ |
| $\eta$ | eta | $1e-1=10^{-1}$ |
| $\beta_1$ | beta1 | $0.9$ |
| $\beta_2$ | beta2 | $0.999$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previoud[1] -> _v | $1e-8=10^{-8}$ |
となっています。
実装例
from typing import Callable, List
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
v = auto()
@dataclass
class AdaBound(BaseOpt):
"""AdaBound optimizer class.
Examples:
>>> import numpy as np
>>> obj = AdaBound()
>>> print(obj)
AdaBound(alpha=0.001, beta1=0.9, beta2=0.999, eta=0.1, eta_l_list=[0.1, 0.999], eta_u_list=[0.1, 0.999])
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00316221, -0.00316226])
"""
kind: InitVar[int] = 2
alpha: float = 1e-3
beta1: float = 0.9
beta2: float = 0.999
eta: float = 1e-1
eta_l: Callable = field(
default=lambda eta, beta2, t: eta*(1 - 1/((1-beta2)*t + 1)),
repr=False)
eta_u: Callable = field(
default=lambda eta, beta2, t: eta*(1 + 1/((1-beta2)*t)),
repr=False)
eta_l_list: List = field(default_factory=list)
eta_u_list: List = field(default_factory=list)
def __post_init__(self, *args, **kwds):
super().__post_init__(*args, **kwds)
if not self.eta_l_list:
self.eta_l_list = [self.eta, self.beta2]
if not self.eta_u_list:
self.eta_u_list = [self.eta, self.beta2]
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.beta1)*(grad-self._m)
self._v += (1-self.beta2)*(grad*grad - self._v)
eta_hat = np.clip(self.alpha/np.sqrt(self._v),
self.eta_l(*self.eta_l_list, t),
self.eta_u(*self.eta_u_list, t))
delta = -eta_hat/np.sqrt(t)*self._m
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
AMSBound
AdaBoundと同様です。
こちらはAMSGradを改良したものになります。
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L} (w_t) \\
m_t &= \beta_1 m_{t-1} + (1-\beta_1) g_t \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\
\hat{v}_t &= \textrm{max}(\hat{v}_{t-1}, v_t) \\
\hat{\eta}_t &= \textrm{clip}\left( \cfrac{\alpha}{\sqrt{v_t}}, \left[ \eta_l(t), \eta_u(t) \right] \right) \\
\eta_t &= \cfrac{\hat{\eta}_t}{\sqrt{t}} \\
\Delta w_t &= - \eta_t m_t \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
実装に際して第二式および第三式を
\begin{align}
m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\beta_1)(g_t - m_{t-1}) \\
v_t &= \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\
\Leftrightarrow
v_t &= v_{t-1} + (1-\beta_2)(g_t^2 - v_{t-1})
\end{align}
のように式変形しています。
$\eta_l$や$\eta_u$はAdaBoundと同じように計算しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha_0$ | alpha | $1e-3=10^{-3}$ |
| $\eta$ | eta | $1e-1=10^{-1}$ |
| $\beta_1$ | beta1 | $0.9$ |
| $\beta_2$ | beta2 | $0.999$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $v_0$ | previous[1] -> _v | $1e-8=10^{-8}$ |
| $\hat{v}_0$ | previous[2] -> _hat_v | $1e-8=10^{-8}$ |
となっています。
実装例
from typing import Callable, List
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
v = auto()
v_hat = auto()
@dataclass
class AMSBound(BaseOpt):
"""AMSBound optimizer class.
Examples:
>>> import numpy as np
>>> obj = AMSBound()
>>> print(obj)
AMSBound(alpha=0.001, beta1=0.9, beta2=0.999, eta=0.1, eta_l_list=[0.1, 0.999], eta_u_list=[0.1, 0.999])
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00316221, -0.00316226])
"""
kind: InitVar[int] = 3
alpha: float = 1e-3
beta1: float = 0.9
beta2: float = 0.999
eta: float = 1e-1
eta_l: Callable = field(
default=lambda eta, beta2, t: eta*(1 - 1/((1-beta2)*t + 1)),
repr=False)
eta_u: Callable = field(
default=lambda eta, beta2, t: eta*(1 + 1/((1-beta2)*t)),
repr=False)
eta_l_list: List = field(default_factory=list)
eta_u_list: List = field(default_factory=list)
def __post_init__(self, *args, **kwds):
super().__post_init__(*args, **kwds)
if not self.eta_l_list:
self.eta_l_list = [self.eta, self.beta2]
if not self.eta_u_list:
self.eta_u_list = [self.eta, self.beta2]
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.beta1)*(grad-self._m)
self._v += (1-self.beta2)*(grad*grad - self._v)
self._v_hat = np.maximum(self._v_hat, self._v)
eta_hat = np.clip(self.alpha/np.sqrt(self._v),
self.eta_l(*self.eta_l_list, t),
self.eta_u(*self.eta_u_list, t))
delta = -eta_hat/np.sqrt(t)*self._m
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _v(self):
return self.previous[_keys.v]
@_v.setter
def _v(self, value):
self.previous[_keys.v] = value
@property
def _v_hat(self):
return self.previous[_keys.v_hat]
@_v_hat.setter
def _v_hat(self, value):
self.previous[_keys.v_hat] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
AdaBelief
次に載せるSAMのついでに実装しました。ほぼAdamなので実装は超楽でした笑。
詳しくはこちらの記事をご覧ください。
\begin{align}
g_t &= \nabla_{w_t}\mathcal{L}(w_t) \\
m_t &= \beta_1 m_{t-1} + (1- \beta_1) g_t \\
s_t &= \beta_2 s_{t-1} + (1- \beta_2) (g_t - m_t)^2 \\
\alpha_t &= \alpha_0 \cfrac{\sqrt{1-\beta_2^t}}{1- \beta_1^t} \\
\Delta w_t &= - \alpha_t \cfrac{m_t}{\sqrt{s_t + \varepsilon}} \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
一見するとどこが違うのか戸惑いますが、$v_t$の式が(ここや論文では文字の混同を避けるために$s_t$ですが)勾配の2乗ではなく勾配とモーメント移動平均との差の2乗になっています。
これにより平坦な勾配に対しても急峻な勾配に対しても大きな更新幅を実現しつつ、最適値付近では小さな更新幅を実現しています。
実装に際して第二式および第三式を
\begin{align}
m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \\
\Leftrightarrow
m_t &= m_{t-1} + (1-\beta_1)(g_t - m_{t-1}) \\
s_t &= \beta_2 s_{t-1} + (1-\beta_2)(g_t - m_t)^2 \\
\Leftrightarrow
s_t &= s_{t-1} + (1-\beta_2)\left\{(g_t - m_t)^2 - s_{t-1} \right\}
\end{align}
のように式変形しています。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\alpha_0$ | alpha | $1e-3=10^{-3}$ |
| $\beta_1$ | beta1 | $0.9$ |
| $\beta_2$ | beta2 | $0.999$ |
| $m_0$ | previous[0] -> _m | $1e-8=10^{-8}$ |
| $s_0$ | previous[1] -> _v | $1e-8=10^{-8}$ |
となっています。
実装例
from enum import IntEnum, auto
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
class _keys(IntEnum):
m = 0
s = auto()
@dataclass
class AdaBelief(BaseOpt):
"""AdaBelief optimizer class.
Examples:
>>> import numpy as np
>>> obj = AdaBelief()
>>> print(obj)
AdaBelief(alpha=0.001, beta1=0.9, beta2=0.999)
>>> obj.update(np.array([-0.5, 1]))
array([ 0.00099998, -0.001 ])
"""
kind: InitVar[int] = 2
alpha: float = 1e-3
beta1: float = 0.9
beta2: float = 0.999
def update(self, grad, *args, t=1, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
self._m += (1-self.beta1)*(grad-self._m)
self._s += (1-self.beta2)*((grad-self._m)**2 - self._s)
alpha_t = self.alpha*np.sqrt(1 - self.beta2**t)/(1 - self.beta1**t)
delta = -alpha_t*self._m/np.sqrt(self._s)
return delta
@property
def _m(self):
return self.previous[_keys.m]
@_m.setter
def _m(self, value):
self.previous[_keys.m] = value
@property
def _s(self):
return self.previous[_keys.s]
@_s.setter
def _s(self, value):
self.previous[_keys.s] = value
if __name__ == "__main__":
import doctest
doctest.testmod()
SAM
ちょうど最適化手法の実装手直しをしていたところにこんな記事が上がってきたら実装してみるしかない、ということでやってみました。合ってる...のか?
\begin{align}
g_t &= \nabla_{w_t} \mathcal{L} (w_t) \\
\epsilon (w_t) &= \rho \textrm{sign} (g_t) \cfrac{|g_t|^{q-1}}{\left( \| g_t \|^q_q \right)^{1 - \frac{1}{q}}} \\
\mathcal{G}_t &= \nabla_{w_t} \mathcal{L} (w_t + \epsilon (w_t)) \\
\Delta w_t &= opt(\mathcal{G}_t) \\
w_{t+1} &= w_t + \Delta w_t
\end{align}
ちょっとNAGに似てますね。簡単に説明すると
- 現在の勾配から移動先を決定して
- その移動先での勾配を求め
- 求めた勾配を用いて更新幅を決定する
という感じです。更新幅の決定はこれまで紹介した様々な最適化手法を利用できるようで、論文ではシンプルにSGDを利用しています。
このような更新方法を行うことで目的関数のより平坦な部分へと収束しようとするようです。詳しくは先ほどのリンク先Qiita記事や論文をご参照ください。
ハイパーパラメータは
| 記号 | コード内表記 | 値 |
|---|---|---|
| $\rho$ | rho | $5e-2=5 \times 10^{-2}$ |
| $q$ | q | $2$ |
としています。もちろん使用する最適化手法用のハイパーパラメータは別途指定する必要があります。
実装例
import sys
from typing import Any, Union, Dict
from dataclasses import dataclass, InitVar, field
import numpy as np
from numpy import ndarray
try:
from ._base import BaseOpt
except:
from _base import BaseOpt
@dataclass
class SAM(BaseOpt):
"""SAM optimizer class."""
parent: Any = None #: BaseLayer = None
q: int = 2
rho: float = 5e-2
opt: Union[str, BaseOpt] = "adam"
opt_dict: Dict[str, Any] = field(default_factory=dict)
def __post_init__(self, *args, **kwds):
super().__post_init__(*args, **kwds)
try:
from ._interface import get_opt
except:
from _interface import get_opt
self.opt = get_opt(self.opt, *args, **self.opt_dict)
def update(self, grad, *args, **kwds):
"""Update calculation.
Args:
grad (ndarray): Gradient propagating from the lower layer.
t (int): Timestep.
Returns:
delta (ndarray): Update delta.
"""
eps = self._epsilon(grad)
self.parent.params += eps
_ = self.parent.forward(self.parent.x, *args, **kwds)
grad = self.parent.backward(self.parent.grad, *args, **kwds)
self.parent.params -= eps
return self.opt.update(grad, *args, **kwds)
def _epsilon(self, grad):
return (self.rho * np.sign(grad) * np.abs(grad)**(self.q-1)
/ np.linalg.norm(
grad if isinstance(grad, ndarray) else np.array([grad]),
ord=self.q)**(1 - 1/self.q))
if __name__ == "__main__":
import doctest
doctest.testmod()
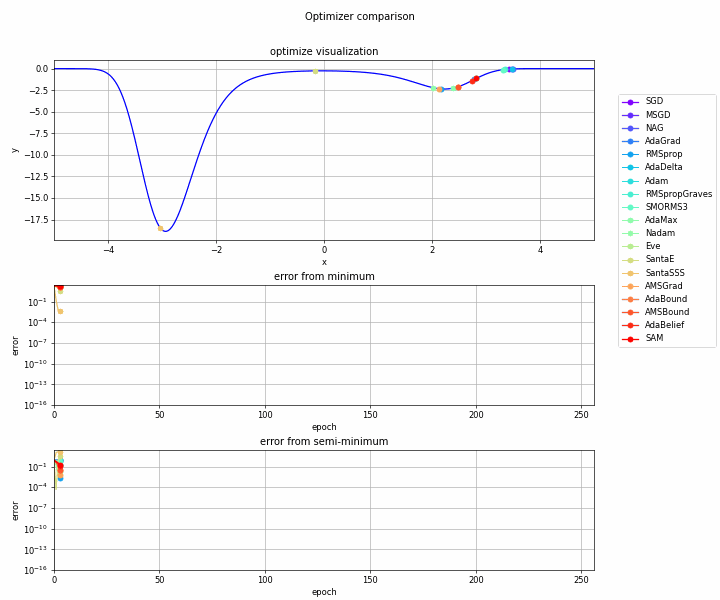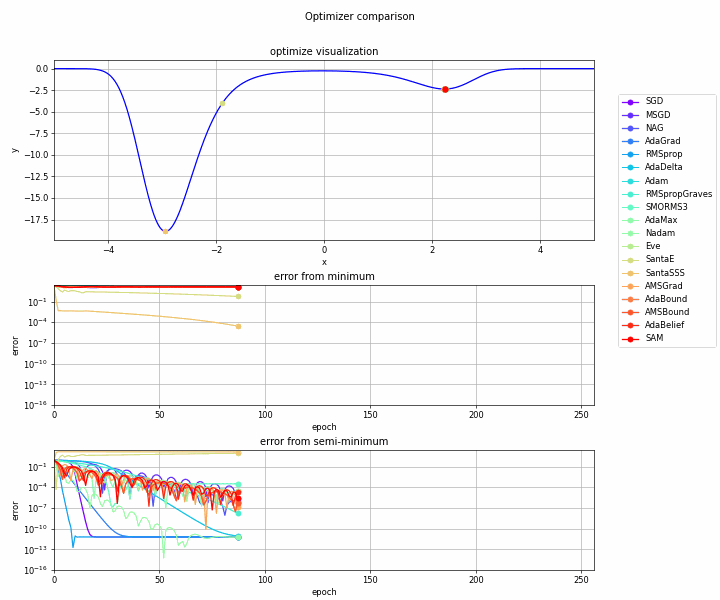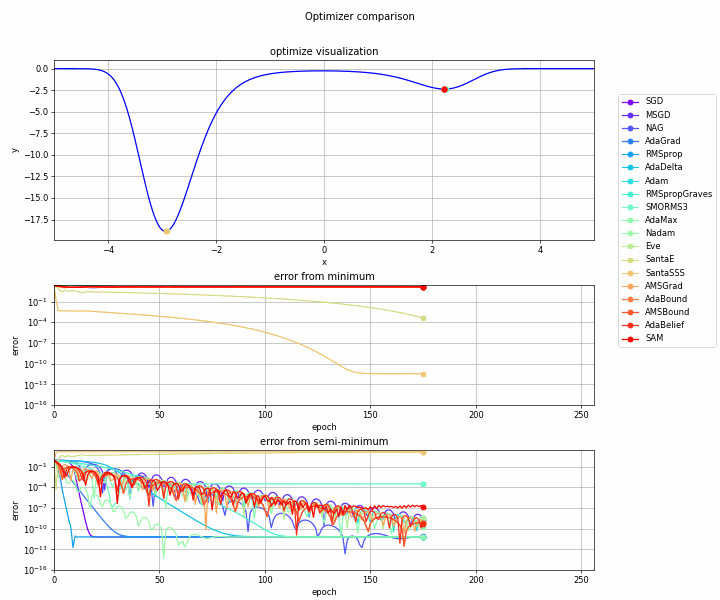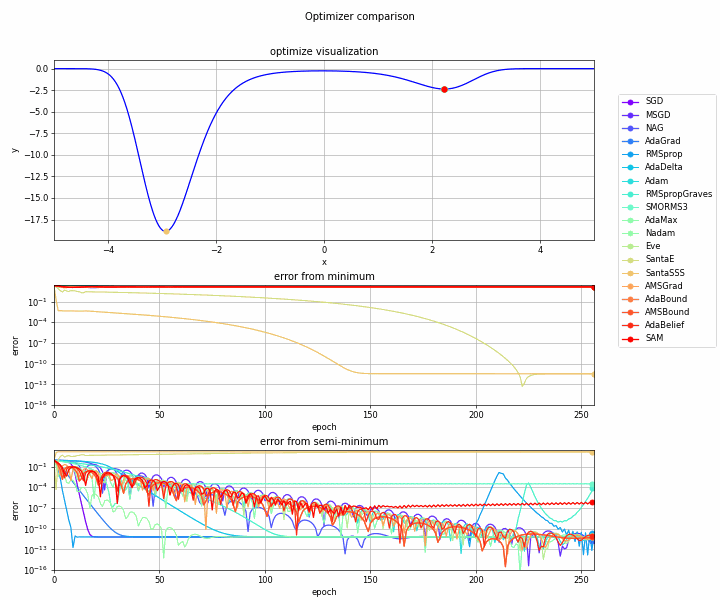
実験
実験してみます。
実験コード
from dataclasses import dataclass
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
from _interface import get_opt
@dataclass
class _target():
params: float
x: float = 0 # dummy for NAG.
grad: float = 0 # dummy for NAG.
def forward(self, *args, **kwds):
"""
Maxima = -0.257043 (when x = -0.0383009)
Minimal = -2.36643 (when x = 2.22366)
= -2.93536 (when x = -2.93536)
"""
return -np.exp(-((self.params+4)*(self.params+1)
*(self.params-1)*(self.params-3)/14 + 0.5))
def backward(self, *args, **kwds):
"""
https://www.wolframalpha.com/input/?i=-exp%28-%28%28x+%2B+4%29%28x+%2B+1%29%28x+%E2%88%92+1%29%28x+%E2%88%92+3%29%2F14+%2B+0.5%29%29&lang=ja
"""
return (0.173294*np.exp(
-((self.params+4)*(self.params+1)
*(self.params-1)*(self.params-3)/14))
*(self.params**3 + 0.75 * self.params**2 - 6.5*self.params - 0.25))
def opt_plot():
start_x = 3.5
objective = _target(start_x)
objective.params = start_x
start_y = objective.forward()
x_range = np.arange(-5, 5, 1e-2)
objective.params = x_range
y_range = objective.forward()
exact_x = -2.93536
objective.params = exact_x
exact_y = objective.forward()
semi_exact_x = 2.22366
epoch = 256
frame = 64
fps = 10
np.random.seed(seed=2)
opt_dict = {
"SGD": get_opt("sgd", n=1, eta=0.1),
"MSGD": get_opt("msgd", n=1, eta=0.25),
"NAG": get_opt("nag", n=1, parent=objective, eta=0.1),
"AdaGrad": get_opt("adagrad", n=1, eta=0.25),
"RMSprop": get_opt("rmsprop", n=1, eta=0.05),
"AdaDelta": get_opt("adadelta", n=1, rho=0.9999),
"Adam": get_opt("adam", n=1, alpha=0.25),
"RMSpropGraves": get_opt("rmspropgraves", n=1, eta=0.0125),
"SMORMS3": get_opt("smorms3", n=1, eta=0.05),
"AdaMax": get_opt("adamax", n=1, alpha=0.5),
"Nadam": get_opt("nadam", n=1, alpha=0.5),
"Eve": get_opt("eve", n=1, f_star=exact_y, alpha=0.25),
"SantaE": get_opt("santae", n=1, burnin=epoch/2**4, N=1,
eta=0.0125),
"SantaSSS": get_opt("santasss", n=1, burnin=epoch/2**4, N=1,
eta=0.125),
"AMSGrad": get_opt("amsgrad", n=1, alpha=0.125),
"AdaBound": get_opt("adabound", n=1, alpha=0.125),
"AMSBound": get_opt("amsbound", n=1, alpha=0.125),
"AdaBelief": get_opt("adabelief", n=1, alpha=0.25),
"SAM": get_opt("sam", n=1, parent=objective,
opt_dict={"n": 1, "alpha": 0.25})
}
key_len = len(max(opt_dict.keys(), key=len))
current_x = np.full(len(opt_dict), start_x)
current_y = np.full(len(opt_dict), start_y)
err_list = [[] for i in range(len(opt_dict))]
semi_err_list = [[] for i in range(len(opt_dict))]
cmap = plt.get_cmap("rainbow")
coloring = [cmap(i) for i in np.linspace(0, 1, len(opt_dict))]
fig, ax = plt.subplots(3, 1, figsize=(12, 10), dpi=60)
fig.suptitle("Optimizer comparison")
ax[0].set_title("optimize visualization")
ax[0].set_position([0.075, 0.6, 0.75, 0.3])
ax[0].set_xlabel("x")
ax[0].set_ylabel("y")
ax[0].grid()
ax[0].set_xlim([x_range[0], x_range[-1]])
ax[0].set_ylim([np.min(y_range)-1, np.max(y_range)+1])
ax[1].set_title("error from minimum")
ax[1].set_position([0.075, 0.325, 0.75, 0.2])
ax[1].set_xlabel("epoch")
ax[1].set_ylabel("error")
ax[1].set_yscale("log")
ax[1].grid()
ax[1].set_xlim([0, epoch])
ax[1].set_ylim([1e-16, 25])
ax[2].set_title("error from semi-minimum")
ax[2].set_position([0.075, 0.05, 0.75, 0.2])
ax[2].set_xlabel("epoch")
ax[2].set_ylabel("error")
ax[2].set_yscale("log")
ax[2].grid()
ax[2].set_xlim([0, epoch])
ax[2].set_ylim([1e-16, 25])
base, = ax[0].plot(x_range, y_range, color="b")
images = []
for i in range(1, epoch+1):
imgs = []
for j, opt in enumerate(opt_dict):
err = 0.5 * (current_x[j] - exact_x)**2
semi_err = 0.5 * (current_x[j] - semi_exact_x)**2
err_list[j].append(err)
semi_err_list[j].append(semi_err)
if i % (epoch//frame) == 0:
img, = ax[0].plot(current_x[j], current_y[j],
color=coloring[j], marker="o")
err_img, = ax[1].plot(err_list[j], color=coloring[j])
err_point, = ax[1].plot(i-1, err, color=coloring[j],
marker="o")
semi_err_img, = ax[2].plot(semi_err_list[j], color=coloring[j])
semi_err_point, = ax[2].plot(i-1, semi_err, color=coloring[j],
marker="o")
imgs.extend([img, err_img, err_point,
semi_err_img, semi_err_point])
objective.params = current_x[j]
dw = opt_dict[opt].update(objective.backward(),
t=i, f=current_y[j])
objective.params += dw
current_x[j] += dw
current_y[j] = objective.forward()
if imgs:
images.append([base]+imgs)
imgs = []
for j, opt in enumerate(opt_dict):
img, = ax[0].plot(current_x[j], current_y[j],
marker="o", color=coloring[j], label=opt)
imgs.append(img)
print(f"{opt.rjust(key_len)} method get {current_x[j]}.")
err = 0.5 * (current_x[j] - exact_x)**2
semi_err = 0.5 * (current_x[j] - semi_exact_x)**2
err_list[j].append(err)
semi_err_list[j].append(semi_err)
img, = ax[1].plot(err_list[j], color=coloring[j])
imgs.append(img)
img, = ax[1].plot(epoch, err, color=coloring[j], marker="o")
imgs.append(img)
img, = ax[2].plot(semi_err_list[j], color=coloring[j])
imgs.append(img)
img, = ax[2].plot(i-1, semi_err, color=coloring[j], marker="o")
imgs.append(img)
images.append([base]+imgs)
fig.legend(bbox_to_anchor=(1., 0.85))
ani = anim.ArtistAnimation(fig, images)
ani.save("optimizers.gif", writer="pillow", fps=fps)
if __name__ == "__main__":
opt_plot()
おわりに
すごく時間かかった...間違いなど発見された方は是非教えてください。
参考
- 深層学習の最適化アルゴリズム
- 【2020決定版】スーパーわかりやすい最適化アルゴリズム -損失関数からAdamとニュートン法-
- matplotlibで異なる色をプロットする
- matplotlib の legend(凡例) の 位置を調整する
- matplotlib逆引きメモ(フレーム編)