対象者
CNNを用いた画像認識で登場するim2col関数について詳しく知りたい方へ
初期の実装から改良版、バッチ・チャンネル対応版、ストライド・パディング対応版までgifや画像を用いて徹底解説します。
目次
im2colとは
im2colは、画像認識において用いられている関数です。動作としては多次元配列を2次元配列へ、可逆的に変換します。
これの最大のメリットは高速な行列演算ができるnumpyの恩恵を最大限に受けられることでしょう。
これなくして今日の画像認識の発展はなかったと言っても過言ではありません(たぶん)。
なぜ必要か
画像はもともと2次元のデータ構造をしていると思いますよね？
見た目は確かに2次元ですが、実際に機械学習する際はRGBに分解した(これをチャンネルといいます)画像を用いることが多いです。
つまり、カラー画像は3次元のデータ構造をしていることになります。
また、白黒画像はチャンネル数が1ですが、一度の伝播で複数の画像を流す(これをバッチといいます)ので、3次元のデータ構造となります。
実用上、わざわざ白黒画像だけ3次元にして実装するのは効率が悪いので、白黒画像はチャンネル数1としてカラー画像と揃え、合計で4次元のデータ構造をしています。
二重ループを用いれば１枚ずつ画像に処理をかけていくことができますが、それではnumpyの利点を消してしまいます(numpyはforループなどで回すと遅いという性質があります)。
そのため4次元のデータを2次元にすることでnumpyの利点を最大限活かすことができるim2colという関数が必要となるのです。
CNNとは
CNNとは、Convolutional Neural Network: 畳み込みニューラルネットワークの略で、ある座標点とその周囲の座標点に深い関係があるデータに対して用いられます。簡単な例で言えば画像や動画ですね。
CNN登場以前は画像などのデータ構造をニューラルネットワークを用いて学習する場合、2次元のデータを平滑化して1次元のデータとして扱っており、2次元のデータが持つ重要な相関関係を無視していました。
CNNは画像という2次元のデータ構造を保ったまま特徴量を抜き出していくことで画像認識にブレークスルーを引き起こしました。
網膜から視神経への情報伝達の際に行われている処理から着想を得ている技術であり、より人間の認識に近い処理を行うことが可能となりました。
フィルタリング
CNNの処理の内容は主にフィルタリング(畳み込み層)とプーリング(プーリング層)と呼ばれる処理です。
フィルタリングとは、画像データから例えば縦線などの特徴を検出する処理を行うものです。
これは人間の網膜細胞が行っている処理と似ています(人間の網膜細胞では特定のパターンに反応し電気信号を発して情報を視神経に伝える細胞があります)。
プーリングとはフィルタリングで抜き出した特徴量のうち、より特徴的な物を抜き出す処理を行うものです。
これは人間の視神経で行われている処理と似ています(視神経から脳へ情報が伝達される時点で神経細胞の数が減っている→情報が圧縮されている)。
データ量削減の観点からこれは非常に優秀な処理で、特徴量をうまく残しながらメモリ節約および計算量を削減することができます。
プーリングの実装にもim2colと別の記事で紹介する予定のcol2imが活躍しますが、今回は特にフィルタリングに注目します。
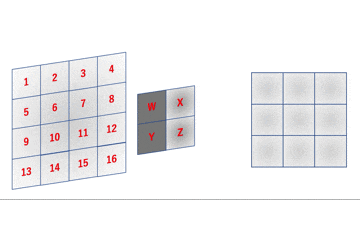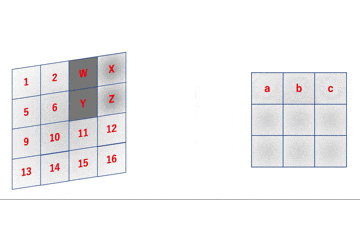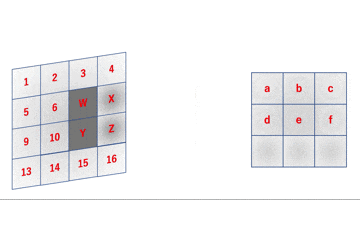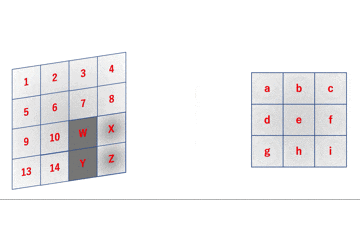
上のgifはフィルタリングのイメージを表したものです。
im2colの動作と初期の実装
im2colの実装を理解するために、その動作を数式と画像とgifを用いて徹底的に解剖します。
im2colの動作
先のgifは数式的には
a = 1W + 2X + 5Y + 6Z \\
b = 2W + 3X + 6Y + 7Z \\
c = 3W + 4X + 7Y + 8Z \\
d = 5W + 6X + 9Y + 10Z \\
e = 6W + 7X + 10Y + 11Z \\
f = 7W + 8X + 11Y + 12Z \\
g = 9W + 10X + 13Y + 14Z \\
h = 10W + 11X + 14Y + 15Z \\
i = 11W + 12X + 15Y + 16Z
のようになります。im2colはこれを行列積演算で実現するためにいい感じに画像データを変形します。
数式でも確認します。
\begin{align}
\left(
\begin{array}{c}
a \\
b \\
c \\
d \\
e \\
f \\
g \\
h \\
i
\end{array}
\right)^{\top}
&=
\left(
\begin{array}{cccc}
W & X & Y & Z
\end{array}
\right)
\left(
\begin{array}{ccccccccc}
1 & 2 & 3 & 5 & 6 & 7 & 9 & 10 & 11 \\
2 & 3 & 4 & 6 & 7 & 8 & 10 & 11 & 12 \\
5 & 6 & 7 & 9 & 10 & 11 & 13 & 14 & 15 \\
6 & 7 & 8 & 10 & 11 & 12 & 14 & 15 & 16
\end{array}
\right) \\
&=
\left(
\begin{array}{c}
1W + 2X + 5Y + 6Z \\
2W + 3X + 6Y + 7Z \\
3W + 4X + 7Y + 8Z \\
5W + 6X + 9Y + 10Z \\
6W + 7X + 10Y + 11Z \\
7W + 8X + 11Y + 12Z \\
8W + 9X + 12Y + 13Z \\
10W + 11X + 14Y + 15Z \\
11W + 12X + 15Y + 16Z
\end{array}
\right)^{\top}
\end{align}
im2colの初期の実装
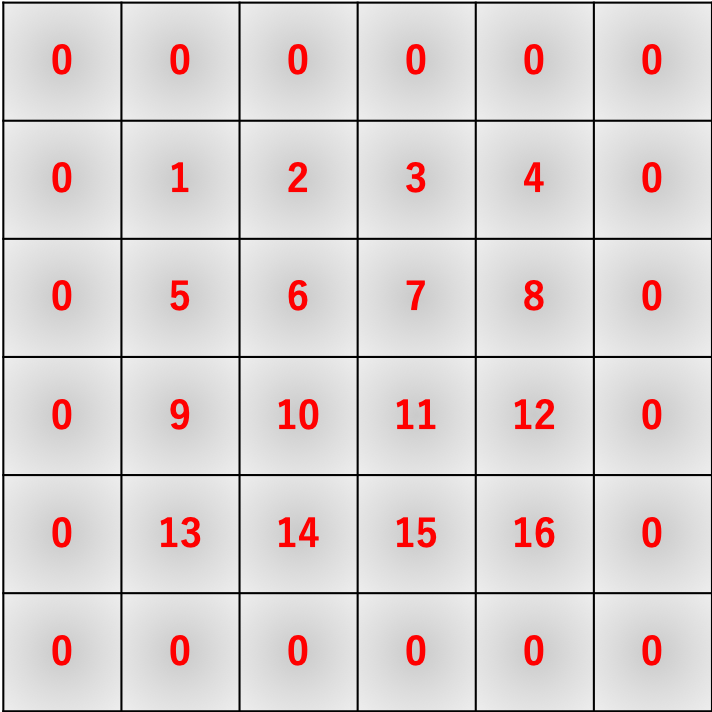
画像から、出力行列のサイズは$(I_h - F_h + 1) \times (I_w - F_w + 1) = O_h \times O_w$のように計算することができます。
つまり、$O_h O_w$個の要素が必要となるため、im2colの列数は$O_h O_w$となります。
一方で、行数はフィルタのサイズに比例しますので$F_hF_w$となるため、$I_h \times I_w$の入力行列に$F_h \times F_w$のフィルタをかける時、im2colの出力行列は$F_h F_w \times O_h O_w$となります。
以上をプログラムに落とし込むと次のようになります。
初期のim2col
import time
import numpy as np
def im2col(image, F_h, F_w):
I_h, I_w = image.shape
O_h = I_h - F_h + 1
O_w = I_w - F_w + 1
col = np.empty((F_h*F_w, O_h*O_w))
for h in range(O_h):
for w in range(O_w):
col[:, w + h*O_w] = image[h : h+F_h, w : w+F_w].reshape(-1)
return col
x = np.arange(1, 17).reshape(4, 4)
f = np.arange(-4, 0).reshape(2, 2)
print(im2col(x, 2, 2))
print(im2col(f, 2, 2).T)
print(im2col(f, 2, 2).T @ im2col(x, 2, 2))
行列のサイズに関しての計算は上記の通りです。
以下では実際に変形しているところの実装を見てみます。
for h in range(O_h):
for w in range(O_w):
col[:, w + h*O_w] = image[h : h+F_h, w : w+F_w].reshape(-1)
各h, wに対応する出力行列への書き込み場所は以下の通りです。
col[:, w + h*O_w]で指定されている書き込み場所ですね。ここに入力行列の該当箇所image[h : h+F_h, w : w+F_w]を.reshape(-1)で平滑化して代入しています。
まだ簡単ですね。
初期のim2colの問題点
さて、early_im2col.pyには重大な欠点が存在します。
その欠点とは、先にも述べた通りnumpyはforなどのループ処理でアクセスすると遅くなるという欠点に由来するものです。
一般に、early_im2dol.pyで動作例として紹介している入力配列xはもっとずっと大きいものです(例えばすごく画像サイズの小さいデータセットであるMNISTの手書き数字画像は$28 \times 28$の行列です)。
処理時間を計測してみましょう。
y = np.zeros((28, 28))
start = time.time()
for i in range(1000):
im2col(y, 2, 2)
end = time.time()
print("time: {}".format(end - start))
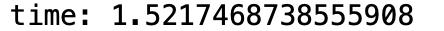高々$28 \times 28$の行列に対して1000回処理を行っただけで1.5秒もの時間がかかってしまいます。
MNISTデータベースは実に6万枚もの手書き数字データベースですので、単純計算で全ての画像に１回ずつフィルタリングするだけで**900秒**かかる計算になります。
実際の機械学習では複数のフィルタを数多の回数かけるため、これでは実用的ではありません。
改良版im2col(初期ver)
問題点を復習すると、つまりforループでnumpy配列にアクセスする回数が多いことが問題であることがわかります。ということはアクセス回数を減らせば良いわけです。
early_im2col.pyでは、numpy配列であるimageに$O_h O_w$回アクセスしており、$28 \times 28$の入力行列に$2 \times 2$のフィルタをかける処理ではアクセス回数は実に$27 \times 27 = 729$回となります。
ところで、一般に出力行列よりもフィルタの方が圧倒的にサイズが小さいため、これを利用すると等価な処理でnumpy配列へのアクセス回数を劇的に減らすことができます。
それが改良版im2col(初期ver)です。
なかなかトリッキーなことをしています。
改良版`im2col`(初期ver)
import time
import numpy as np
def im2col(image, F_h, F_w):
I_h, I_w = image.shape
O_h = I_h - F_h + 1
O_w = I_w - F_w + 1
col = np.empty((F_h, F_w, O_h, O_w))
for h in range(F_h):
for w in range(F_w):
col[h, w, :, :] = image[h : h+O_h, w : w+O_w]
return col.reshape(F_h*F_w, O_h*O_w)
x = np.arange(1, 17).reshape(4, 4)
f = np.arange(-4, 0).reshape(2, 2)
print(im2col(x, 2, 2))
print(im2col(f, 2, 2).T)
print(im2col(f, 2, 2).T @ im2col(x, 2, 2))
y = np.zeros((28, 28))
start = time.time()
for i in range(1000):
im2col(y, 2, 2)
end = time.time()
print("time: {}".format(end - start))
結果はご覧の通り、150倍もの高速化に成功しました！
これなら6万枚に1回ずつ処理を行っても6秒で済むため(先ほどよりは)実用的になりました。
では、具体的に何がどう変わったのかを追っていきます。
変更点1
まず最初の変更点としては、出力行列のメモリ確保部分ですね。
col = np.empty((F_h, F_w, O_h, O_w))
こんな感じで4次元のデータ構造でメモリを確保しています。
変更点2
続いての変更点は、アクセス回数を減らすためにループ回数を$O_h O_w$から$F_h F_w$にしているところですね。
for h in range(F_h):
for w in range(F_w):
col[h, w, :, :] = image[h : h+O_h, w : w+O_w]
これにより、MNIST画像一枚あたりのnumpy配列アクセス回数が729回からなんと4回にまで減少します！
また、各ループでの出力配列へのアクセス場所と入力配列へのアクセス場所は以下のようになっています。
このようにアクセスすると以下のような出力配列ができます。
変更点3
最後に出力時に求める形状に整形します。
return col.reshape(F_h*F_w, O_h*O_w)
numpyの動作的には$(F_h, F_w, O_h, O_w)$を平滑化した$(F_h F_w O_h O_w, )$の１次元データを$(F_h F_w, O_h O_w)$の２次元データに変形している感じです。
もっと噛み砕いて言うと、図の一つ一つの2次元データを1次元に平滑化して下に積んでいく感じです。
上手いこと考えますよね〜
多次元配列への拡張
さて、im2colとはで述べたように、本来この関数の対象の行列は4次元のデータ構造をしています。
フィルタも入力行列のチャンネル数分はまず確保し、それに加えてそのセットを$M$個用意した4次元のデータ構造をしています。
これを加味してimproved_early_im2col.pyを修正していきます。
数式で追いかける
まずは数学的にどのような形状に変形する必要があるかを考えましょう。
カラー画像の構造は、チャンネル数を$C$、バッチサイズを$B$とすると$(B, C, I_h, I_w)$という構造をしています。
一方でフィルタは$(M, C, F_h, F_w)$という構造をしています。
improved_early_im2col.pyでは$(I_h, I_w)$の行列に$(F_h, F_w)$のフィルタをかける場合出力される行列が$(F_h F_w, O_h O_w)$および$(1, F_h F_w)$でしたね。
$B=1$と$M=1$を仮定すると、フィルタリングを行列積で計算させるためには、im2colで変形された入力データとフィルタの形状のそれぞれの行と列が一致していなければならないため、$(C F_h F_w, O_h O_w)$および$(1, C F_h F_w)$となります。
また、一般的に$B \ne M$であるから、これらは$C F_h F_w$とは関係ない方に組み合わせる必要があります。
これらの事実を組み合わせると、im2colで出力されるべき配列の形状は$(C F_h F_w, B O_h O_w)$および$(M, C F_h F_w)$となります。
ついでに、フィルタリングの計算結果としては$(M, C F_h F_w) \times (C F_h F_w, B O_h O_w) = (M, B O_h O_w)$となり、これをreshapeして次元を入れ替えた$(B, M, O_h, O_w):=(B, C', I_h', I_w')$が次の層への入力として伝播していきます。
実装してみる
実装内容はほとんどimproved_early_im2col.pyと変わりません。上位にバッチとチャンネルの次元を追加しただけです。
バッチ・チャンネル対応`im2col`
import time
import numpy as np
def im2col(images, F_h, F_w):
B, C, I_h, I_w = images.shape
O_h = I_h - F_h + 1
O_w = I_w - F_w + 1
cols = np.empty((B, C, F_h, F_w, O_h, O_w))
for h in range(F_h):
for w in range(F_w):
cols[:, :, h, w, :, :] = images[:, :, h : h+O_h, w : w+O_w]
return cols.transpose(1, 2, 3, 0, 4, 5).reshape(C*F_h*F_w, B*O_h*O_w)
x = np.arange(1, 3*3*4*4+1).reshape(3, 3, 4, 4)
f = np.arange(-3*3*2*2, 0).reshape(3, 3, 2, 2)
print(im2col(x, 2, 2))
print(im2col(f, 2, 2).T)
print(np.dot(im2col(f, 2, 2).T, im2col(x, 2, 2)))
y = np.zeros((100, 3, 28, 28))
start = time.time()
for i in range(10):
im2col(y, 2, 2)
end = time.time()
print("time: {}".format(end - start))
最大の変化は返り値の部分ですね。
return cols.transpose(1, 2, 3, 0, 4, 5).reshape(C*F_h*F_w, B*O_h*O_w)
ここでは、numpyのtranspose関数を用いて次元の順番を入れ替えています。
それぞれ以下のように対応しており、順番を入れ替えてからreshapeすることで正しい出力を返します。
\begin{array}{ccccccc}
(&0, &1, &2, &3, &4, &5) \\
(&B, &C, &F_h, &F_w, &O_h, &O_w)
\end{array}
\xrightarrow[\textrm{transpose}]{入れ替え}
\begin{array}{ccccccc}
(&1, &2, &3, &0, &4, &5) \\
(&C, &F_h, &F_w, &B, &O_h, &O_w)
\end{array}
\xrightarrow[\textrm{reshape}]{変形}
(C F_h F_w, B O_h O_w)
これでバッチ・チャンネルにも対応したim2colが完成です！
ストライドとパディング
さて、これで終わりかと思いきやそうでもなかったりします。最後に紹介するのはストライドとパディングと呼ばれる処理です。
いずれもより効率的で効果的なCNNの実装には不可欠な要素です。
ストライド
これまでの実装では、当たり前のようにフィルタは１マスずつズレていましたよね？
このズレる量のことをストライドといいますが、これは何も1マスずつでなければならないという決まりはありません。
実際の画像はわずか1ピクセルズレるだけで情報が大きく変わるような場面の方が少ないため、大抵の場合ストライドは1ではないでしょう。
パディング
ストライドと違ってパディングはこれまでの実装で一切触れられていません。
その主な役目はフィルタリングによって出力画像のサイズが変わらないようにすることと、画像の端の方の情報を余さず得ることです。
具体的には入力画像の周囲を$0$で埋めることでフィルタが動く範囲を広げています。
ストライドとパディングの実装
ではそれぞれの実装について見ていきます。
ストライドの実装
ストライドの実装はそんなに難しくないですね。これまでのストライド移動幅を1から変更できるようにするだけです。
今まで
cols[:, :, h, w, :, :] = images[:, :, h : h+O_h, w : w+O_w]
のようにしていましたが、これを
cols[:, :, h, w, :, :] = images[:, :, h : h + stride*O_h : stride, w : w + stride*O_w : stride]
のように変更します。
初期版の動きはこんな感じで
数式では
a = 1W + 2X + 5Y + 6Z \\
b = 3W + 4X + 7Y + 8Z \\
c = 9W + 10X + 13Y + 14Z \\
d = 11W + 12X + 15Y + 16Z \\
\Leftrightarrow \left(
\begin{array}{c}
a \\
b \\
c \\
d
\end{array}
\right)^{\top}
=
\left(
\begin{array}{cccc}
W & X & Y & Z
\end{array}
\right)
\left(
\begin{array}{cccc}
1 & 3 & 9 & 11 \\
2 & 4 & 10 & 12 \\
5 & 7 & 13 & 15 \\
6 & 8 & 14 & 16
\end{array}
\right)
こんな感じで、改良版だとこんな感じですね。
やっぱりトリッキーですね...これ考えた人凄すぎです。
パディングの実装
一方パディングの処理の実装は至ってシンプルです。
numpyにあるpad関数を用いて
images = np.pad(images, [(0, 0), (0, 0), (pad, pad), (pad, pad)], "constant")
とすればOK。
pad関数の動作は結構ややこしいので(後日紹介します)、とりあえず上記の解説をしておきます。
padの第一引数は対象の配列です。これは大丈夫でしょう。
問題は第二引数です。
[(0, 0), (0, 0), (pad, pad), (pad, pad)]
pad関数にこのように入力すると、
- １次元目は
(0, 0)、つまりパディングなし - 2次元目は
(0, 0)、つまりパディングなし - 3次元目は
(pad, pad)、つまり上下の増量幅padで0埋め("constant") - 4次元目は
(pad, pad)、つまり左右の増量幅padで0埋め("constant")
第三引数はいくつか指定できるものがありますが、今回は0埋めしたいので"constant"を指定しています。
詳しくは公式ドキュメントを見てください。
出力次元の計算
さて、上記の変更を施して実行してもまだエラーが出て動きませんね。はい。
理由はお察しの通り、ストライドとパディングの実装とともに出力次元が変わるからです。どのように変わるのか考えて見ましょう。
ストライドの影響
ストライド幅を増やすとフィルタをかける回数が反比例的に減少します。
フィルタを1マスごとにかけるか2マスごとにかけるかで回数が半減することは察しがつくでしょう。
数式で表すと
O_h = \left\lceil \cfrac{I_h - F_h}{\textrm{stride}} \right\rceil + 1\\
O_w = \left\lceil \cfrac{I_w - F_w}{\textrm{stride}} \right\rceil + 1
という感じになります。
$I_h = 4, F_h = 2, \textrm{stride} = 1$の場合は
$O_h = \left\lceil \cfrac{4 - 2}{1} \right\rceil + 1 = 3$
となり、$I_h = 4, F_h = 2, \textrm{stride} = 2$の場合は
$O_h = \left\lceil \cfrac{4 - 2}{2} \right\rceil + 1 = 2$
となり、これまでの画像と一致することが確認できますね。
パディングの影響
パディングの影響はすごくシンプルです。入力画像1枚ごとのサイズが上下$+ \textrm{pad}_{ud}$、左右$+ \textrm{pad}_{lr}$されるため、
I_h \leftarrow I_h + 2\textrm{pad}_{ud} \\
I_w \leftarrow I_w + 2\textrm{pad}_{lr}
と置き換えればよく、つまり
O_h = \left\lceil \cfrac{I_h - F_h + 2\textrm{pad}_{ud}}{\textrm{stride}} \right\rceil + 1 \\
O_w = \left\lceil \cfrac{I_w - F_w + 2\textrm{pad}_{lr}}{\textrm{stride}} \right\rceil + 1
となります。
また逆に、出力画像のサイズを入力画像のサイズに揃えたい場合は$O_h = I_h$および$O_w = I_w$なので
\textrm{pad}_{ud} = \left\lceil \cfrac{1}{2}\left\{(I_h - 1) \textrm{stride} - I_h + F_h\right\} \right\rceil \\
\textrm{pad}_{lr} = \left\lceil \cfrac{1}{2}\left\{(I_w - 1) \textrm{stride} - I_w + F_w\right\} \right\rceil \\
のように計算できます。
ついでにストライドも自由度を上げておきましょう。
O_h = \left\lceil \cfrac{I_h - F_h + 2\textrm{pad}_{ud}}{\textrm{stride}_{ud}} \right\rceil + 1 \\
O_w = \left\lceil \cfrac{I_w - F_w + 2\textrm{pad}_{lr}}{\textrm{stride}_{lr}} \right\rceil + 1 \\
\textrm{pad}_{ud} = \left\lceil \cfrac{1}{2}\left\{(I_h - 1) \textrm{stride}_{ud} - I_h + F_h\right\} \right\rceil \\
\textrm{pad}_{lr} = \left\lceil \cfrac{1}{2}\left\{(I_w - 1) \textrm{stride}_{lr} - I_w + F_w\right\} \right\rceil
完成版im2col
ストライドとパディングを加味して自由度を上げたim2colは次のようになります。
ついでにいくつかカスタマイズも施しておきます。
im2col.py
import numpy as np
def im2col(images, filters, stride=1, pad=0):
if images.ndim == 2:
images = images.reshape(1, 1, *images.shape)
elif images.ndim == 3:
B, I_h, I_w = images.shape
images = images.reshape(B, 1, I_h, I_w)
B, C, I_h, I_w = images.shape
if isinstance(filters, tuple):
if len(filters) == 2:
filters = (1, 1, *filters)
elif len(filters) == 3:
M, F_h, F_w = filters
filters = (M, 1, F_h, F_w)
_, _, F_h, F_w = filters
else:
if filters.ndim == 2:
filters = filters.reshape(1, 1, *filters.shape)
elif filters.ndim == 3:
M, F_h, F_w = filters.shape
filters = filters.reshape(M, 1, F_h, F_w)
_, _, F_h, F_w = filters.shape
if isinstance(stride, tuple):
stride_ud, stride_lr = stride
else:
stride_ud = stride
stride_lr = stride
if isinstance(pad, tuple):
pad_ud, pad_lr = pad
elif isinstance(pad, int):
pad_ud = pad
pad_lr = pad
elif pad == "same":
pad_ud = 0.5*((I_h - 1)*stride_ud - I_h + F_h)
pad_lr = 0.5*((I_w - 1)*stride_lr - I_w + F_w)
pad_zero = (0, 0)
O_h = int((I_h - F_h + 2*pad_ud)//stride_ud + 1)
O_w = int((I_w - F_w + 2*pad_lr)//stride_lr + 1)
result_pad = (pad_ud, pad_lr)
pad_ud = int(np.ceil(pad_ud))
pad_lr = int(np.ceil(pad_lr))
pad_ud = (pad_ud, pad_ud)
pad_lr = (pad_lr, pad_lr)
images = np.pad(images, [pad_zero, pad_zero, pad_ud, pad_lr], \
"constant")
cols = np.empty((B, C, F_h, F_w, O_h, O_w))
for h in range(F_h):
h_lim = h + stride_ud*O_h
for w in range(F_w):
w_lim = w + stride_lr*O_w
cols[:, :, h, w, :, :] \
= images[:, :, h:h_lim:stride_ud, w:w_lim:stride_lr]
results = []
results.append(cols.transpose(1, 2, 3, 0, 4, 5).reshape(C*F_h*F_w, B*O_h*O_w))
results.append((O_h, O_w))
results.append(result_pad)
return results
簡単に解説していきます。
整形など
def im2col(images, filters, stride=1, pad=0):
if images.ndim == 2:
images = images.reshape(1, 1, *images.shape)
elif images.ndim == 3:
B, I_h, I_w = images.shape
images = images.reshape(B, 1, I_h, I_w)
B, C, I_h, I_w = images.shape
if isinstance(filters, tuple):
if len(filters) == 2:
filters = (1, 1, *filters)
elif len(filters) == 3:
M, F_h, F_w = filters
filters = (M, 1, F_h, F_w)
_, _, F_h, F_w = filters
else:
if filters.ndim == 2:
filters = filters.reshape(1, 1, *filters.shape)
elif filters.ndim == 3:
M, F_h, F_w = filters.shape
filters = filters.reshape(M, 1, F_h, F_w)
_, _, F_h, F_w = filters.shape
if isinstance(stride, tuple):
stride_ud, stride_lr = stride
else:
stride_ud = stride
stride_lr = stride
if isinstance(pad, tuple):
pad_ud, pad_lr = pad
elif isinstance(pad, int):
pad_ud = pad
pad_lr = pad
elif pad == "same":
pad_ud = 0.5*((I_h - 1)*stride_ud - I_h + F_h)
pad_lr = 0.5*((I_w - 1)*stride_lr - I_w + F_w)
pad_zero = (0, 0)
- 引数の数を削減するためにフィルタそのものを引数に取るように変更
- 入力画像が4次元でなければ４次元に変換
- フィルタが４次元でなければ４次元に変換
- バッチサイズ、チャンネル数、入力画像一枚のサイズを取得
- フィルタの数とフィルタのチャンネル数は不要なため捨てて(
_, _, ...の部分)、フィルタ一枚のサイズを取得 -
strideがtupleなら上下と左右のストライド幅を個別に指定しているとみなし、そうでなければ同じ値を用いる -
padがtupleなら上下と左右のパディング幅を個別に指定しているとみなし、そうでなければ同じ値を用いる -
pad == "same"と指定された場合は、入力画像のサイズを維持するパディング幅を**floatで計算**(後の出力サイズ計算のため)
という感じの処理をしています。
準備
O_h = int((I_h - F_h + 2*pad_ud)//stride_ud + 1)
O_w = int((I_w - F_w + 2*pad_lr)//stride_lr + 1)
result_pad = (pad_ud, pad_lr)
pad_ud = int(np.ceil(pad_ud))
pad_lr = int(np.ceil(pad_lr))
pad_ud = (pad_ud, pad_ud)
pad_lr = (pad_lr, pad_lr)
images = np.pad(images, [pad_zero, pad_zero, pad_ud, pad_lr], \
"constant")
cols = np.empty((B, C, F_h, F_w, O_h, O_w))
ここでは
- 出力画像のサイズを計算
- 可読性の向上のためにパディングをタプルに変更する
- 入力画像にパディングを施す
- 出力用配列のメモリ確保
を行っています。
処理本体と返り値
for h in range(F_h):
h_lim = h + stride_ud*O_h
for w in range(F_w):
w_lim = w + stride_lr*O_w
cols[:, :, h, w, :, :] \
= images[:, :, h:h_lim:stride_ud, w:w_lim:stride_lr]
results = []
results.append(cols.transpose(1, 2, 3, 0, 4, 5).reshape(C*F_h*F_w, B*O_h*O_w))
results.append((O_h, O_w))
results.append(result_pad)
return results
最後に、処理本体と返り値についてです。
- 可読性の向上のため、
h_limとw_limという変数を新たに用意し、フィルタリング処理の右端と下端を定義 - ストライド幅ごとに入力画像から値を取得し出力用配列
colsに格納 - 次元を入れ替えて変形して返す
- さらに、出力行列の形状とパディングの形状を返す
MNISTで実験
KerasのデータセットからMNISTのデータをダウンロードして実験してみます。
mnist_test.py
#%pip install tensorflow
#%pip install keras
from keras.datasets import mnist
import matplotlib.pyplot as plt
# 取得する枚数を指定
B = 3
# データセット取得
(x_train, _), (_, _) = mnist.load_data()
x_train = x_train[:B]
# 表示してみる
fig, ax = plt.subplots(1, B)
for i, x in enumerate(x_train):
ax[i].imshow(x, cmap="gray")
fig.tight_layout()
plt.savefig("mnist_data.png")
plt.show()
# 縦線を検出してみる
M = 1
C = 1
F_h = 7
F_w = 7
_, I_h, I_w = x_train.shape
f = np.zeros((F_h, F_w))
f[:, int(F_w/2)] = 1
no_pad, (O_h, O_w), _ = im2col(x_train, f, stride=2, pad="same")
filters, _, _ = im2col(f, f)
y = np.dot(filters.T, no_pad).reshape(M, B, O_h, O_w).transpose(1, 0, 2, 3).reshape(B, O_h, O_w)
fig2, ax2 = plt.subplots(1, B)
for i, x in enumerate(y):
ax2[i].imshow(x[F_h : I_h-F_h, F_w : I_w-F_w], cmap="gray")
fig2.tight_layout()
plt.savefig("vertical_filtering.png")
plt.show()
# 横線を検出してみる
f = np.zeros((F_h, F_w))
f[int(F_h / 2), :] = 1
no_pad, (O_h, O_w), _ = im2col(x_train, f, stride=2, pad="same")
filters, _, _ = im2col(f, f)
y = np.dot(filters.T, no_pad).reshape(M, B, O_h, O_w).transpose(1, 0, 2, 3).reshape(B, O_h, O_w)
fig3, ax3 = plt.subplots(1, B)
for i, x in enumerate(y):
ax3[i].imshow(x[F_h : I_h-F_h, F_w : I_w-F_w], cmap="gray")
fig3.tight_layout()
plt.savefig("horizontal_filtering.png")
plt.show()
# 右下がりを検出してみる
f = np.zeros((F_h, F_w))
for i in range(F_h):
f[i, i] = 1
no_pad, (O_h, O_w), _ = im2col(x_train, f, stride=2, pad="same")
filters, _, _ = im2col(f, f)
y = np.dot(filters.T, no_pad).reshape(M, B, O_h, O_w).transpose(1, 0, 2, 3).reshape(B, O_h, O_w)
fig4, ax4 = plt.subplots(1, B)
for i, x in enumerate(y):
ax4[i].imshow(x[F_h : I_h-F_h, F_w : I_w-F_w], cmap="gray")
fig4.tight_layout()
plt.savefig("right_down_filtering.png")
plt.show()
# 右上がりを検出してみる
f = np.zeros((F_h, F_w))
for i in range(F_h):
f[F_h - i - 1, i] = 1
no_pad, (O_h, O_w), _ = im2col(x_train, f, stride=2, pad="same")
filters, _, _ = im2col(f, f)
y = np.dot(filters.T, no_pad).reshape(M, B, O_h, O_w).transpose(1, 0, 2, 3).reshape(B, O_h, O_w)
fig4, ax4 = plt.subplots(1, B)
for i, x in enumerate(y):
ax4[i].imshow(x[F_h : I_h-F_h, F_w : I_w-F_w], cmap="gray")
fig4.tight_layout()
plt.savefig("right_up_filtering.png")
plt.show()
出力結果
元となるデータ  縦線検出結果  横線検出結果  右下がり検出結果  右上がり検出結果 おわりに
以上でim2colについての説明は終了となります。
もしバグやもっとスマートな書き方があればコメントなどでご教授いただけると幸いです。