対象者
前回の記事はこちら
本記事ではこれまで活性化関数一覧や勾配降下法一覧で紹介したactivators.pyやoptimizers.pyを呼び出すための関数get_actとget_optの実装を行います。
また、現在使用されている損失関数についても紹介と実装を行います。
次回の記事はこちら
目次
活性化関数のローカライズ
まずは活性化関数のコード本体を載せておきます。
activators.py
import numpy as np
class Activator():
def __init__(self, *args, **kwds):
pass
def forward(self, *args, **kwds):
raise Exception("Not Implemented")
def backward(self, *args, **kwds):
raise Exception("Not Implemented")
def update(self, *args, **kwds):
pass
class step(Activator):
def forward(self, x, *args, **kwds):
return np.where(x > 0, 1, 0)
def backward(self, x, *args, **kwds):
return np.zeros_like(x)
class identity(Activator):
def forward(self, x, *args, **kwds):
return x
def backward(self, x, *args, **kwds):
return np.ones_like(x)
class bentIdentity(Activator):
def forward(self, x, *args, **kwds):
return 0.5*(np.sqrt(x**2 + 1) - 1) + x
def backward(self, x, *args, **kwds):
return 0.5*x/np.sqrt(x**2 + 1) + 1
class hardShrink(Activator):
def __init__(self, lambda_=0.5, *args, **kwds):
self.lambda_ = lambda_
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where((-self.lambda_ <= x) & (x <= self.lambda_),
0, x)
def backward(self, x, *args, **kwds):
return np.where((-self.lambda_ <= x) & (x <= self.lambda_),
0, 1)
class softShrink(Activator):
def __init__(self, lambda_=0.5, *args, **kwds):
self.lambda_ = lambda_
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x < -self.lambda_, x + self.lambda_,
np.where(x > self.lambda_, x - self.lambda_, 0))
def backward(self, x, *args, **kwds):
return np.where((-self.lambda_ <= x) & (x <= self.lambda_),
0, 1)
class threshold(Activator):
def __init__(self, threshold, value, *args, **kwds):
self.threshold = threshold
self.value = value
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x > self.threshold, x, self.value)
def backward(self, x, *args, **kwds):
return np.where(x > self.threshold, 1, 0)
class sigmoid(Activator):
def forward(self, x, *args, **kwds):
return 1/(1 + np.exp(-x))
def backward(self, x, y, *args, **kwds):
return y*(1 - y)
class hardSigmoid(Activator):
def forward(self, x, *args, **kwds):
return np.clip(0.2*x + 0.5, 0, 1)
def backward(self, x, *args, **kwds):
return np.where((x > 2.5) | (x < -2.5), 0, 0.2)
class logSigmoid(Activator):
def forward(self, x, *args, **kwds):
return -np.log(1 + np.exp(-x))
def backward(self, x, *args, **kwds):
return 1/(1 + np.exp(x))
class act_tanh(Activator):
def forward(self, x, *args, **kwds):
return np.tanh(x)
def backward(self, x, *args, **kwds):
return 1 - np.tanh(x)**2
class hardtanh(Activator):
def forward(self, x, *args, **kwds):
return np.clip(x, -1, 1)
def backward(self, x, *args, **kwds):
return np.where((-1 <= x) & (x <= 1), 1, 0)
class tanhShrink(Activator):
def forward(self, x, *args, **kwds):
return x - np.tanh(x)
def backward(self, x, *args, **kwds):
return np.tanh(x)**2
class ReLU(Activator):
def forward(self, x, *args, **kwds):
return np.maximum(0, x)
def backward(self, x, *args, **kwds):
return np.where(x > 0, 1, 0)
class ReLU6(Activator):
def forward(self, x, *args, **kwds):
return np.clip(x, 0, 6)
def backward(self, x, *args, **kwds):
return np.where((0 < x) & (x < 6), 1, 0)
class leakyReLU(Activator):
def __init__(self, alpha=1e-2, *args, **kwds):
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.maximum(self.alpha * x, x)
def backward(self, x, *args, **kwds):
return np.where(x < 0, self.alpha, 1)
class ELU(Activator):
def __init__(self, alpha=1., *args, **kwds):
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x >= 0, x, self.alpha*(np.exp(x) - 1))
def backward(self, x, *args, **kwds):
return np.where(x >= 0, 1, self.alpha*np.exp(x))
class SELU(Activator):
def __init__(self, lambda_=1.0507, alpha=1.67326, *args, **kwds):
self.lambda_ = lambda_
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x >= 0,
self.lambda_*x,
self.lambda_*self.alpha*(np.exp(x) - 1))
def backward(self, x, *args, **kwds):
return np.where(x >= 0,
self.lambda_,
self.lambda_*self.alpha*np.exp(x))
class CELU(Activator):
def __init__(self, alpha=1., *args, **kwds):
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x >= 0,
x,
self.alpha*(np.exp(x/self.alpha) - 1))
def backward(self, x, *args, **kwds):
return np.where(x >= 0, 1, np.exp(x/self.alpha))
class softmax(Activator):
def forward(self, x, *args, **kwds):
return np.exp(x)/np.sum(np.exp(x))
def backward(self, x, *args, **kwds):
return np.exp(x)*(np.sum(np.exp(x))
- np.exp(x))/np.sum(np.exp(x))**2
class softmin(Activator):
def forward(self, x, *args, **kwds):
return np.exp(-x)/np.sum(np.exp(-x))
def backward(self, x, *args, **kwds):
return -(np.exp(x)*(np.sum(np.exp(-x)) - np.exp(x))
/np.sum(np.exp(-x))**2)
class logSoftmax(Activator):
def forward(self, x, *args, **kwds):
return np.log(np.exp(x)/np.sum(np.exp(x)))
def backward(self, x, *args, **kwds):
y = np.sum(np.exp(x))
return (y - np.exp(x))/y
class softplus(Activator):
def forward(self, x, *args, **kwds):
return np.logaddexp(x, 0)
def backward(self, x, *args, **kwds):
return 1/(1 + np.exp(-x))
class softsign(Activator):
def forward(self, x, *args, **kwds):
return x/(1 + np.abs(x))
def backward(self, x, *args, **kwds):
return 1/(1 + np.abs(x)) ** 2
class Swish(Activator):
def __init__(self, beta=1, *args, **kwds):
self.beta = beta
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return x/(1 + np.exp(-self.beta*x))
def backward(self, x, y, *args, **kwds):
return self.beta*y + (1 - self.beta*y)/(1 + np.exp(-self.beta*x))
def d2y(self, x, *args, **kwds):
return (-0.25*self.beta*(self.beta*x*np.tanh(0.5*self.beta*x) - 2)
*(1 - np.tanh(0.5*self.beta*x)**2))
class Mish(Activator):
def forward(self, x, *args, **kwds):
return x*np.tanh(np.logaddexp(x, 0))
def backward(self, x, *args, **kwds):
omega = (4*(x + 1) + 4*np.exp(2*x)
+ np.exp(3*x) + (4*x + 6)*np.exp(x))
delta = 2*np.exp(x) + np.exp(2*x) + 2
return np.exp(x)*omega/delta**2
def d2y(self, x, *args, **kwds):
omega = (2*(x + 2)
+ np.exp(x)*(np.exp(x)*(-2*np.exp(x)*(x - 1) - 3*x + 6)
+ 2*(x + 4)))
delta = np.exp(x)*(np.exp(x) + 2) + 2
return 4*np.exp(x)*omega/delta**3
class tanhExp(Activator):
def forward(self, x, *args, **kwds):
return x*np.tanh(np.exp(x))
def backward(self, x, *args, **kwds):
tanh_exp = np.tanh(np.exp(x))
return tanh_exp - x*np.exp(x)*(tanh_exp**2 - 1)
def d2y(self, x, *args, **kwds):
tanh_exp = np.tanh(np.exp(x))
return (np.exp(x)*(-x + 2*np.exp(x)*x*tanh_exp - 2)
*(tanh_exp**2 - 1))
class maxout(Activator):
def __init__(self, n_prev, n, k, wb_width=5e-2, *args, **kwds):
self.n_prev = n_prev
self.n = n
self.k = k
self.w = wb_width*np.random.rand((n_prev, n*k))
self.b = wb_width*np.random.rand(n*k)
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
self.x = x.copy()
self.z = np.dot(self.w.T, x) + self.b
self.z = self.z.reshape(self.n, self.k)
self.y = np.max(self.z, axis=1)
return self.y
def backward(self, g, *args, **kwds):
self.dw = np.sum(np.dot(self.w, self.x))
get_act.py
_act_dic = {"step": step,
"identity": identity,
"bent-identity": bentIdentity,
"hard-shrink": hardShrink,
"soft-shrink": softShrink,
"threshold": threshold,
"sigmoid": sigmoid,
"hard-sigmoid": hardSigmoid,
"log-sigmoid": logSigmoid,
"tanh": act_tanh,
"tanh-shrink": tanhShrink,
"hard-tanh":hardtanh,
"ReLU": ReLU,
"ReLU6": ReLU6,
"leaky-ReLU": leakyReLU,
"ELU": ELU,
"SELU": SELU,
"CELU": CELU,
"softmax": softmax,
"softmin": softmin,
"log-softmax": logSoftmax,
"softplus": softplus,
"softsign": softsign,
"Swish": Swish,
"Mish": Mish,
"tanhExp": tanhExp,
}
def get_act(name, *args, **kwds):
if name in _act_dic.keys():
activator = _act_dic[name](*args, **kwds)
else:
raise ValueError(name, ": Unknown activator")
return activator
勾配降下法のローカライズ
続いて勾配降下法のローカライズです。やり方は同じですね。
optimizers.py
import numpy as np
class Optimizer():
"""
最適化手法が継承するスーパークラス。
"""
def __init__(self, *args, **kwds):
pass
def update(self, *args, **kwds):
pass
class SGD(Optimizer):
def __init__(self, eta=1e-2, *args, **kwds):
super().__init__(*args, **kwds)
self.eta = eta
def update(self, grad_w, grad_b, *args, **kwds):
dw = -self.eta*grad_w
db = -self.eta*grad_b
return dw, db
class MSGD(Optimizer):
def __init__(self, eta=1e-2, mu=0.9, *args, **kwds):
super().__init__(*args, **kwds)
self.eta = eta
self.mu = mu
# 一つ前のステップの値を保持する
self.dw = 0
self.db = 0
def update(self, grad_w, grad_b, *args, **kwds):
dw = self.mu*self.dw - (1-self.mu)*self.eta*grad_w
db = self.mu*self.db - (1-self.mu)*self.eta*grad_b
# コピーではなくビューで代入しているのは、これらの値が使われることはあっても
# 変更されることはないためです。
self.dw = dw
self.db = db
return dw, db
class NAG(Optimizer):
def __init__(self, eta=1e-2, mu=0.9, *args, **kwds):
super().__init__(*args, **kwds)
self.eta = eta
self.mu = mu
# 一つ前のステップの値を保持
self.dw = 0
self.db = 0
def update(self, grad_w, grad_b, w=0, b=0, dfw=None, dfb=None,
nargs=2, *args, **kwds):
if nargs == 1:
grad_w = dfw(w + self.mu*self.dw)
grad_b = 0
elif nargs == 2:
grad_w = dfw(w + self.mu*self.dw, b + self.mu*self.db)
grad_b = dfb(w + self.mu*self.dw, b + self.mu*self.db)
dw = self.mu*self.dw - (1-self.mu)*self.eta*grad_w
db = self.mu*self.db - (1-self.mu)*self.eta*grad_b
# コピーではなくビューで代入しているのは、これらの値が使われることはあっても
# 変更されることはないためです。
self.dw = dw
self.db = db
return dw, db
class AdaGrad(Optimizer):
def __init__(self, eta=1e-3, *args, **kwds):
super().__init__(*args, **kwds)
self.eta = eta
# 一つ前のステップの値を保持する
self.gw = 0
self.gb = 0
def update(self, grad_w, grad_b, *args, **kwds):
self.gw += grad_w*grad_w
self.gb += grad_b*grad_b
dw = -self.eta*grad_w/np.sqrt(self.gw)
db = -self.eta*grad_b/np.sqrt(self.gb)
return dw, db
class RMSprop(Optimizer):
def __init__(self, eta=1e-2, rho=0.99, eps=1e-8, *args, **kwds):
super().__init__(*args, **kwds)
self.eta = eta
self.rho = rho
self.eps = eps
# 一つ前のステップの値を保持する
self.vw = 0
self.vb = 0
def update(self, grad_w, grad_b, *args, **kwds):
self.vw += (1-self.rho)*(grad_w**2 - self.vw)
self.vb += (1-self.rho)*(grad_b**2 - self.vb)
dw = -self.eta*grad_w/np.sqrt(self.vw+self.eps)
db = -self.eta*grad_b/np.sqrt(self.vb+self.eps)
return dw, db
class AdaDelta(Optimizer):
def __init__(self, rho=0.95, eps=1e-6, *args, **kwds):
super().__init__(*args, **kwds)
self.rho = rho
self.eps = eps
# 一つ前のステップの値を保持する
self.vw = 0
self.vb = 0
self.uw = 0
self.ub = 0
def update(self, grad_w, grad_b, *args, **kwds):
self.vw += (1-self.rho)*(grad_w**2 - self.vw)
self.vb += (1-self.rho)*(grad_b**2 - self.vb)
dw = -grad_w*np.sqrt(self.uw+self.eps)/np.sqrt(self.vw+self.eps)
db = -grad_b*np.sqrt(self.ub+self.eps)/np.sqrt(self.vb+self.eps)
self.uw += (1-self.rho)*(dw**2 - self.uw)
self.ub += (1-self.rho)*(db**2 - self.ub)
return dw, db
class Adam(Optimizer):
def __init__(self, alpha=1e-3, beta1=0.9, beta2=0.999, eps=1e-8,
*args, **kwds):
super().__init__(*args, **kwds)
self.alpha = alpha
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
self.mw += (1-self.beta1)*(grad_w - self.mw)
self.mb += (1-self.beta1)*(grad_b - self.mb)
self.vw += (1-self.beta2)*(grad_w**2 - self.vw)
self.vb += (1-self.beta2)*(grad_b**2 - self.vb)
alpha_t = self.alpha*np.sqrt(1-self.beta2**t)/(1-self.beta1**t)
dw = -alpha_t*self.mw/(np.sqrt(self.vw+self.eps))
db = -alpha_t*self.mb/(np.sqrt(self.vb+self.eps))
return dw, db
class RMSpropGraves(Optimizer):
def __init__(self, eta=1e-4, rho=0.95, eps=1e-4, *args, **kwds):
super().__init__(*args, **kwds)
self.eta = eta
self.rho = rho
self.eps = eps
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
def update(self,grad_w, grad_b, *args, **kwds):
self.mw += (1-self.rho)*(grad_w - self.mw)
self.mb += (1-self.rho)*(grad_b - self.mb)
self.vw += (1-self.rho)*(grad_w**2 - self.vw)
self.vb += (1-self.rho)*(grad_b**2 - self.vb)
dw = -self.eta*grad_w/np.sqrt(self.vw - self.mw**2 + self.eps)
db = -self.eta*grad_b/np.sqrt(self.vb - self.mb**2 + self.eps)
return dw, db
class SMORMS3(Optimizer):
def __init__(self, eta=1e-3, eps=1e-8, *args, **kwds):
super().__init__(*args, **kwds)
self.eta = eta
self.eps = eps
# 一つ前のステップの値を保持する
self.zetaw = 0
self.zetab = 0
self.sw = 1
self.sb = 1
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
def update(self, grad_w, grad_b, *args, **kwds):
rhow = 1/(1+self.sw)
rhob = 1/(1+self.sb)
self.mw += (1-rhow)*(grad_w - self.mw)
self.mb += (1-rhob)*(grad_b - self.mb)
self.vw += (1-rhow)*(grad_w**2 - self.vw)
self.vb += (1-rhob)*(grad_b**2 - self.vb)
self.zetaw = self.mw**2 / (self.vw + self.eps)
self.zetaw = self.mb**2 / (self.vb + self.eps)
dw = -grad_w*(np.minimum(self.eta, self.zetaw)
/np.sqrt(self.vw + self.eps))
db = -grad_b*(np.minimum(self.eta, self.zetab)
/np.sqrt(self.vb + self.eps))
self.sw = 1 + (1 - self.zetaw)*self.sw
self.sb = 1 + (1 - self.zetab)*self.sb
return dw, db
class AdaMax(Optimizer):
def __init__(self, alpha=2e-3, beta1=0.9, beta2=0.999,
*args, **kwds):
super().__init__(*args, **kwds)
self.alpha = alpha
self.beta1 = beta1
self.beta2 = beta2
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.uw = 0
self.ub = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
self.mw += (1-self.beta1)*(grad_w - self.mw)
self.mb += (1-self.beta1)*(grad_b - self.mb)
self.uw = np.maximum(self.beta2*self.uw, np.abs(grad_w))
self.ub = np.maximum(self.beta2*self.ub, np.abs(grad_b))
alpha_t = self.alpha/(1 - self.beta1**t)
dw = -alpha_t*self.mw/self.uw
db = -alpha_t*self.mb/self.ub
return dw, db
class Nadam(Optimizer):
def __init__(self, alpha=2e-3, mu=0.975, nu=0.999, eps=1e-8,
*args, **kwds):
super().__init__(*args, **kwds)
self.alpha = alpha
self.mu = mu
self.nu = nu
self.eps = eps
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
self.mw += (1-self.mu)*(grad_w - self.mw)
self.mb += (1-self.mu)*(grad_b - self.mb)
self.vw += (1-self.nu)*(grad_w**2 - self.vw)
self.vb += (1-self.nu)*(grad_b**2 - self.vb)
mhatw = (self.mu*self.mw/(1-self.mu**(t+1))
+ (1-self.mu)*grad_w/(1-self.mu**t))
mhatb = (self.mu*self.mb/(1-self.mu**(t+1))
+ (1-self.mu)*grad_b/(1-self.mu**t))
vhatw = self.nu*self.vw/(1-self.nu**t)
vhatb = self.nu*self.vb/(1-self.nu**t)
dw = -self.alpha*mhatw/np.sqrt(vhatw + self.eps)
db = -self.alpha*mhatb/np.sqrt(vhatb + self.eps)
return dw, db
class Eve(Optimizer):
def __init__(self, alpha=1e-3, beta1=0.9, beta2=0.999, beta3=0.999,
c=10, eps=1e-8, fstar=0, *args, **kwds):
super().__init__(*args, **kwds)
self.alpha = alpha
self.beta1 = beta1
self.beta2 = beta2
self.beta3 = beta3
self.c = c
self.eps = eps
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
self.f = 0
self.fstar = fstar
self.dtilde_w = 0
self.dtilde_b = 0
def update(self, grad_w, grad_b, t=1, f=1, *args, **kwds):
self.mw += (1-self.beta1)*(grad_w - self.mw)
self.mb += (1-self.beta1)*(grad_b - self.mb)
self.vw += (1-self.beta2)*(grad_w**2 - self.vw)
self.vb += (1-self.beta2)*(grad_b**2 - self.vb)
mhatw = self.mw/(1 - self.beta1**t)
mhatb = self.mb/(1 - self.beta1**t)
vhatw = self.vw/(1 - self.beta2**t)
vhatb = self.vb/(1 - self.beta2**t)
if t > 1:
d_w = (np.abs(f-self.fstar)
/(np.minimum(f, self.f) - self.fstar))
d_b = (np.abs(f-self.fstar)
/(np.minimum(f, self.f) - self.fstar))
dhat_w = np.clip(d_w, 1/self.c, self.c)
dhat_b = np.clip(d_b, 1/self.c, self.c)
self.dtilde_w += (1 - self.beta3)*(dhat_w - self.dtilde_w)
self.dtilde_b += (1 - self.beta3)*(dhat_b - self.dtilde_b)
else:
self.dtilde_w = 1
self.dtilde_b = 1
self.f = f
dw = -(self.alpha*mhatw
/(self.dtilde_w*(np.sqrt(vhatw) + self.eps)))
db = -(self.alpha*mhatb
/(self.dtilde_b*(np.sqrt(vhatb) + self.eps)))
return dw, db
class SantaE(Optimizer):
def __init__(self, eta=1e-2, sigma=0.95, lambda_=1e-8,
anne_func=lambda t, n: t**n, anne_rate=0.5,
burnin=100, C=5, N=16,
*args, **kwds):
"""
Args:
eta: Learning rate
sigma: Maybe in other cases;
'rho' in RMSprop, AdaDelta, RMSpropGraves.
'rhow' or 'rhob' in SMORMS3.
'beta2' in Adam, Eve.
'nu' in Nadam.
To use calculation 'v'.
lambda_: Named 'eps'(ε) in other cases.
anne_func: Annealing function.
To use calculation 'beta' at each timestep.
Default is 'timestep'**'annealing rate'.
The calculated value should be towards infinity
as 't' increases.
anne_rate: Annealing rate.
To use calculation 'beta' at each timestep.
The second Argument of 'anne_func'.
burnin: Swith exploration and refinement.
This should be specified by users.
C: To calculate first 'alpha'.
N: Number of minibatch.
"""
super().__init__(*args, **kwds)
self.eta = eta
self.sigma = sigma
self.lambda_ = lambda_
self.anne_func = anne_func
self.anne_rate = anne_rate
self.burnin = burnin
self.N = N
# Keep one step before and Initialize.
self.alpha_w = np.sqrt(eta)*C
self.alpha_b = np.sqrt(eta)*C
self.vw = 0
self.vb = 0
self.gw = 0
self.gb = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
try:
shape_w = grad_w.shape
except:
shape_w = (1, )
try:
shape_b = grad_b.shape
except:
shape_b = (1, )
if t == 1:
# Initialize uw, ub.
self.uw = np.sqrt(self.eta)*np.random.randn(*shape_w)
self.ub = np.sqrt(self.eta)*np.random.randn(*shape_b)
self.vw = (self.sigma*self.vw
+ grad_w*grad_w * (1 - self.sigma) / self.N**2)
self.vb = (self.sigma*self.vb
+ grad_b*grad_b * (1 - self.sigma) / self.N**2)
gw = 1/np.sqrt(self.lambda_ + np.sqrt(self.vw))
gb = 1/np.sqrt(self.lambda_ + np.sqrt(self.vb))
beta = self.anne_func(t, self.anne_rate)
if t < self.burnin:
# Exploration.
self.alpha_w += self.uw*self.uw - self.eta/beta
self.alpha_b += self.ub*self.ub - self.eta/beta
uw = (self.eta/beta * (1 - self.gw/gw)/self.uw
+ np.sqrt(2*self.eta/beta * self.gw)
* np.random.randn(*shape_w))
ub = (self.eta/beta * (1 - self.gb/gb)/self.ub
+ np.sqrt(2*self.eta/beta * self.gb)
* np.random.randn(*shape_b))
else:
# Refinement.
uw = 0
ub = 0
uw += (1 - self.alpha_w)*self.uw - self.eta*gw*grad_w
ub += (1 - self.alpha_b)*self.ub - self.eta*gb*grad_b
# Update values.
self.uw = uw
self.ub = ub
self.gw = gw
self.gb = gb
dw = gw*uw
db = gb*ub
return dw, db
class SantaSSS(Optimizer):
def __init__(self, eta=1e-2, sigma=0.95, lambda_=1e-8,
anne_func=lambda t, n: t**n, anne_rate=0.5,
burnin=100, C=5, N=16,
*args, **kwds):
"""
Args:
eta: Learning rate
sigma: Maybe in other cases;
'rho' in RMSprop, AdaDelta, RMSpropGraves.
'rhow' or 'rhob' in SMORMS3.
'beta2' in Adam, Eve.
'nu' in Nadam.
To use calculation 'v'.
lambda_: Named 'eps'(ε) in other cases.
anne_func: Annealing function.
To use calculation 'beta' at each timestep.
Default is 'timestep'**'annealing rate'.
The calculated value should be towards infinity
as 't' increases.
anne_rate: Annealing rate.
To use calculation 'beta' at each timestep.
The second Argument of 'anne_func'.
burnin: Swith exploration and refinement.
This should be specified by users.
C: To calculate first 'alpha'.
N: Number of minibatch.
"""
super().__init__(*args, **kwds)
self.eta = eta
self.sigma = sigma
self.lambda_ = lambda_
self.anne_func = anne_func
self.anne_rate = anne_rate
self.burnin = burnin
self.N = N
# Keep one step before and Initialize.
self.alpha_w = np.sqrt(eta)*C
self.alpha_b = np.sqrt(eta)*C
self.vw = 0
self.vb = 0
self.gw = 0
self.gb = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
try:
shape_w = grad_w.shape
except:
shape_w = (1, )
try:
shape_b = grad_b.shape
except:
shape_b = (1, )
if t == 1:
# Initialize uw, ub.
self.uw = np.sqrt(self.eta)*np.random.randn(*shape_w)
self.ub = np.sqrt(self.eta)*np.random.randn(*shape_b)
self.vw = (self.sigma*self.vw
+ grad_w*grad_w * (1 - self.sigma) / self.N**2)
self.vb = (self.sigma*self.vb
+ grad_b*grad_b * (1 - self.sigma) / self.N**2)
gw = 1/np.sqrt(self.lambda_ + np.sqrt(self.vw))
gb = 1/np.sqrt(self.lambda_ + np.sqrt(self.vb))
dw = 0.5*gw*self.uw
db = 0.5*gb*self.ub
beta = self.anne_func(t, self.anne_rate)
if t < self.burnin:
# Exploration.
self.alpha_w += (self.uw*self.uw - self.eta/beta)*0.5
self.alpha_b += (self.ub*self.ub - self.eta/beta)*0.5
uw = np.exp(-0.5*self.alpha_w)*self.uw
ub = np.exp(-0.5*self.alpha_b)*self.ub
uw += (-gw*grad_w*self.eta
+ np.sqrt(2*self.gw*self.eta/beta)
* np.random.randn(*shape_w)
+ self.eta/beta*(1-self.gw/gw)/self.uw)
ub += (-gb*grad_b*self.eta
+ np.sqrt(2*self.gb*self.eta/beta)
* np.random.randn(*shape_b)
+ self.eta/beta*(1-self.gb/gb)/self.ub)
uw *= np.exp(-0.5*self.alpha_w)
ub *= np.exp(-0.5*self.alpha_b)
self.alpha_w += (uw*uw - self.eta/beta)*0.5
self.alpha_b += (ub*ub - self.eta/beta)*0.5
else:
# Refinement.
uw = np.exp(-0.5*self.alpha_w)*self.uw
ub = np.exp(-0.5*self.alpha_b)*self.ub
uw -= gw*grad_w*self.eta
ub -= gb*grad_b*self.eta
uw *= np.exp(-0.5*self.alpha_w)
ub *= np.exp(-0.5*self.alpha_b)
# Update values.
self.uw = uw
self.ub = ub
self.gw = gw
self.gb = gb
dw = gw*uw*0.5
db = gb*ub*0.5
return dw, db
class AMSGrad(Optimizer):
def __init__(self, alpha=1e-3, beta1=0.9, beta2=0.999, eps=1e-8,
*args, **kwds):
super().__init__(*args, **kwds)
self.alpha = alpha
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
self.vhatw = 0
self.vhatb = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
self.mw += (1-self.beta1)*(grad_w - self.mw)
self.mb += (1-self.beta1)*(grad_b - self.mb)
self.vw += (1-self.beta2)*(grad_w**2 - self.vw)
self.vb += (1-self.beta2)*(grad_b**2 - self.vb)
self.vhatw = np.maximum(self.vhatw, self.vw)
self.vhatb = np.maximum(self.vhatb, self.vb)
alpha_t = self.alpha / np.sqrt(t)
dw = - alpha_t * self.mw/np.sqrt(self.vhatw + self.eps)
db = - alpha_t * self.mb/np.sqrt(self.vhatb + self.eps)
return dw, db
class AdaBound(Optimizer):
def __init__(self, alpha=1e-3, eta=1e-1, beta1=0.9, beta2=0.999,
eps=1e-8, *args, **kwds):
super().__init__(*args, **kwds)
self.alpha = alpha
self.eta = eta
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
self.mw += (1-self.beta1)*(grad_w - self.mw)
self.mb += (1-self.beta1)*(grad_b - self.mb)
self.vw += (1-self.beta2)*(grad_w**2 - self.vw)
self.vb += (1-self.beta2)*(grad_b**2 - self.vb)
etal = self.eta*(1 - 1/((1-self.beta2)*t + 1))
etau = self.eta*(1 + 1/((1-self.beta2)*t + self.eps))
etahatw_t = np.clip(self.alpha/np.sqrt(self.vw), etal, etau)
etahatb_t = np.clip(self.alpha/np.sqrt(self.vb), etal, etau)
etaw_t = etahatw_t/np.sqrt(t)
etab_t = etahatb_t/np.sqrt(t)
dw = - etaw_t*self.mw
db = - etab_t*self.mb
return dw, db
class AMSBound(Optimizer):
def __init__(self, alpha=1e-3, eta=1e-1, beta1=0.9, beta2=0.999,
eps=1e-8, *args, **kwds):
super().__init__(*args, **kwds)
self.alpha = alpha
self.eta = eta
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
# 一つ前のステップの値を保持する
self.mw = 0
self.mb = 0
self.vw = 0
self.vb = 0
self.vhatw = 0
self.vhatb = 0
def update(self, grad_w, grad_b, t=1, *args, **kwds):
self.mw += (1-self.beta1)*(grad_w - self.mw)
self.mb += (1-self.beta1)*(grad_b - self.mb)
self.vw += (1-self.beta2)*(grad_w**2 - self.vw)
self.vb += (1-self.beta2)*(grad_b**2 - self.vb)
self.vhatw = np.maximum(self.vhatw, self.vw)
self.vhatb = np.maximum(self.vhatb, self.vb)
etal = self.eta*(1 - 1/((1-self.beta2)*t + 1))
etau = self.eta*(1 + 1/((1-self.beta2)*t + self.eps))
etahatw_t = np.clip(self.alpha/np.sqrt(self.vhatw), etal, etau)
etahatb_t = np.clip(self.alpha/np.sqrt(self.vhatb), etal, etau)
etaw_t = etahatw_t/np.sqrt(t)
etab_t = etahatb_t/np.sqrt(t)
dw = - etaw_t*self.mw
db = - etab_t*self.mb
return dw, db
get_opt.py
_opt_dic = {
"SDG": SGD,
"MSGD": MSGD,
"NAG": NAG,
"AdaGrad": AdaGrad,
"RMSprop": RMSprop,
"AdaDelta": AdaDelta,
"Adam": Adam,
"RMSpropGraves": RMSpropGraves,
"SMORMS3": SMORMS3,
"AdaMax": AdaMax,
"Nadam": Nadam,
"Eve": Eve,
"SantaE": SantaE,
"SantaSSS": SantaSSS,
"AMSGrad": AMSGrad,
"AdaBound": AdaBound,
"AMSBound": AMSBound,
}
def get_opt(name, *args, **kwds):
if name in _opt_dic.keys():
optimizer = _opt_dic[name](*args, **kwds)
else:
raise ValueError(name, ": Unknown optimizer")
return optimizer
以上でローカライズは終了です。
損失関数
まずは損失関数とは?から始めます。
深層学習といえばある目的関数をニューラルネットワークで近似したい、という目的がありますね。これは例えば画像認識などの目的関数という物がいまいちわからない問題に対しても実は同じことをしています。例えば手書き数字認識であれば画像を入力して何らかの処理をした結果その数字が出力(正確にはone-hot表現と呼ばれるベクトル)されればいいわけです。
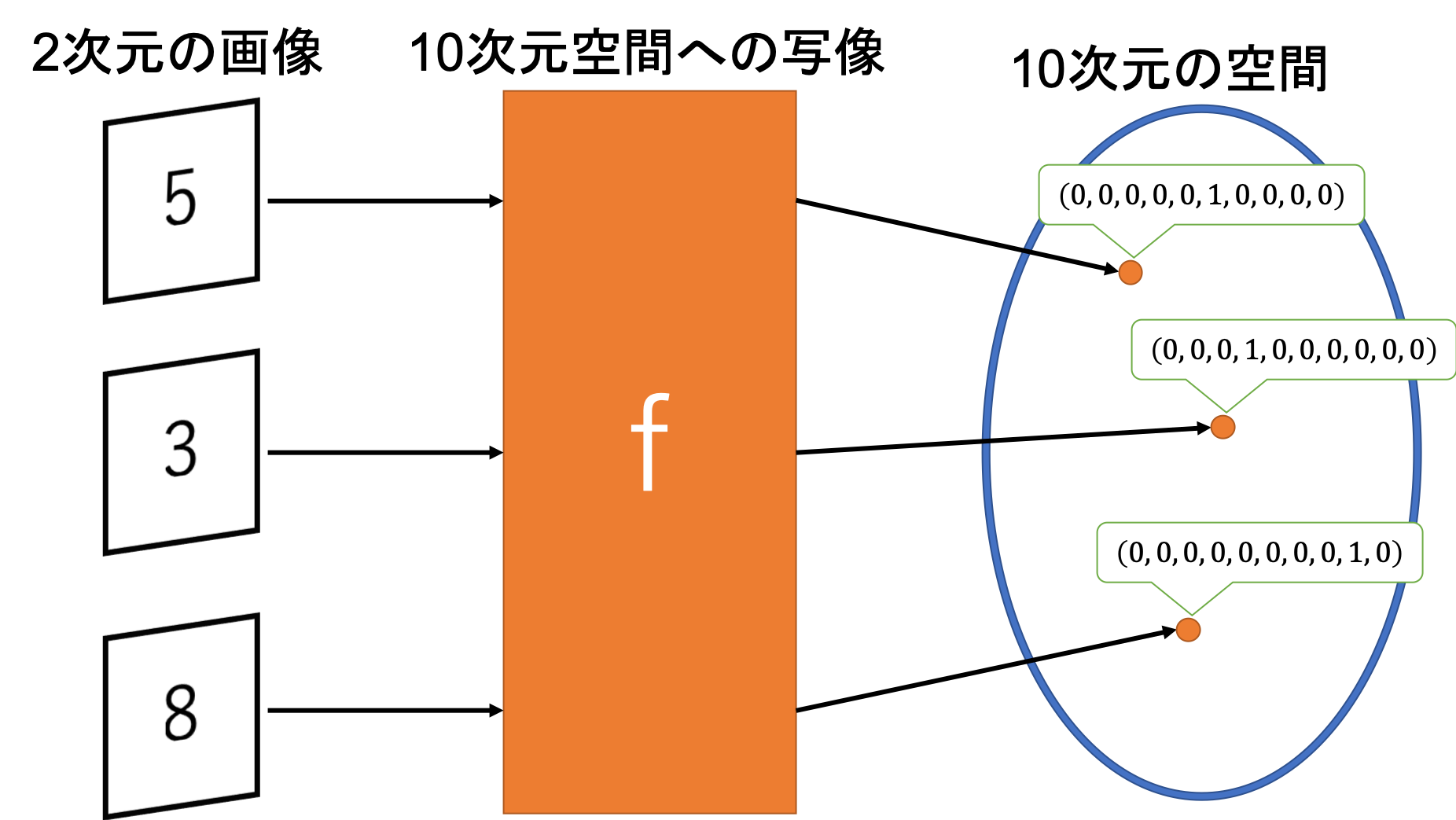
この目的関数についてですが、当然私たちが厳密な関数を知っている場合の方が少ないでしょう。人間が普通に行っている数字認識でも、どのような処理を経て認識しているかは未解明の問題です。
そのため、このままでは学習を進めていく上での指標が存在しません。これではどう学習していけばいいのか、学習している方針が正しいのかどうかがさっぱりですね。目標がないまま勉強するようなものです。
しかし、目的関数の厳密解がわからない以上目的関数との差異をとることはできませんね。ここで登場するのが損失関数という概念です。
一言で言うと「目的関数にどれくらい近いか」ではなく「目的関数とどれくらい離れているか」を学習の指標とします。
教師あり学習を例に挙げると、目的関数での出力(正解値)と近似関数での出力(予測値)がどれほど離れているかを測定し、その差を可能な限りゼロに近づけていくことを考えます。
予測値を計算するのが順伝播、正解値と予測値の誤差を学習のために各パラメータに伝えるのが逆伝播、逆伝播で流れてきた勾配を元にパラメータを更新するのが学習則ですね。
そして、損失関数は逆伝播で流す誤差を決定する関数となります。
損失関数についてはこれくらいでいいでしょう。では具体的にどんな物があるか見ていきましょう。
二乗誤差
まずは線形回帰問題などで用いられる二乗誤差から紹介します。
\mathcal{L}(y) = \cfrac{1}{2} (y - t)^2
$t$は正解値、$y$は予測値です。上式は行列表現となっています。
0.5倍する理由は逆伝播させる際に偏微分を行う必要があり、その時に係数を打ち消すためです。
\cfrac{\partial \mathcal{L}}{\partial y} = \cfrac{1}{2} \times 2(y - t) = y - t
これで逆伝播が簡単に計算できますね。
ちなみに、これは逆伝播のための二乗誤差ですので、学習が収束したかの判定には以下の平均二乗誤差を用います。
E = \cfrac{1}{N}\sum_{i=1}^{N}{\mathcal{L}(y_i)} = \cfrac{1}{N}\sum_{i=1}^{N}{\cfrac{1}{2}(y_i - t_i)^2}
Nはデータ数ですね。この値がほとんど変化しなくなったら学習が収束した(十分な精度かは保証しません)ことを表します。
実装は以下の通りです。ある意味でレイヤーのような扱いをするためにクラスとして、forwardとbackward関数を実装しています。
errors.py
class SquareError(Error):
def forward(self, y, t, *args, **kwds):
self.error = 0.5 * (y - t)**2
return self.error
def backward(self, y, t, *args, **kwds):
return y - t
二値交差エントロピー
続いて二値交差エントロピーです。こちらは出力層の活性化関数がsigmoid関数である場合にフィッティングされた誤差関数になります。つまり二値分類問題に用いられる損失関数ですね。
\mathcal{L}(y) = - t \log y - (1 - t) \log(1 - y)
微分は
\cfrac{\partial \mathcal{L}}{\partial y} = \cfrac{y - t}{y(1 - y)}
となっており、分母にsigmoid関数の微分が現れていますね。このため出力層を伝播する勾配が
\underbrace{\cfrac{y - t}{y(1 - y)}}_{損失関数の微分} \times \underbrace{y(1 - y)}_{\textrm{sigoid関数の微分}} = y - t
のように簡単な形になりますね。
errors.py
class BinaryCrossEntropy(Error):
def forward(self, y, t, *args, **kwds):
self.error = - t*np.log(y) - (1 - t)*np.log(1 - y)
return self.error
def backward(self, y, t, *args, **kwds):
return (y - t) / (y*(1 - y))
交差エントロピー
次は多値分類問題で出力層の活性化関数にsoftmax関数を用いる場合に使用される交差エントロピー誤差です。
\mathcal{L}(y) = - t \log y
二値交差エントロピーの一般形といっていいでしょう。微分は
\cfrac{\partial \mathcal{L}}{\partial y_i} = -\cfrac{t_i}{y_i}
となりますが、出力層の活性化関数にsoftmax関数を用いている場合は、入力$x_i$についての偏微分を考えると
\begin{align}
\left( \cfrac{\partial \mathcal{L}}{\partial y} \times \cfrac{\partial y}{\partial x} \right)_i &= \sum_{j=1}^{n}{\left( \cfrac{\partial \mathcal{L}}{\partial y_j} \times \cfrac{\partial y_j}{\partial x_i} \right)} \\
&= \sum_{j=1}^{n}{
\left\{ \begin{array}{ccc}
-\cfrac{t_i}{y_i} \times y_i (1 - y_i) & = t_i y_i - t_i & (j=i) \\
-\cfrac{t_j}{y_j} \times (-y_i y_j) &= t_j y_i & (j \ne i)
\end{array} \right\}
} \\
&= \underbrace{(\underbrace{t_i y_i}^{これと} - t_i)}_{j=i} + \underbrace{y_i \sum_{j=1, j\ne i}^{n}{t_j}}_{j \ne i}^{これをまとめると} \\
&= \underbrace{y_i \sum_{j=1}^{n}{t_j}}^{こうなる} - t_i \\
&= y_i - t_i \quad (\because \textrm{one-hot}ベクトルなので \sum_{j=1}^{n}{t_j} = 1 となる)
\end{align}
のように綺麗な形となります。計算グラフだと
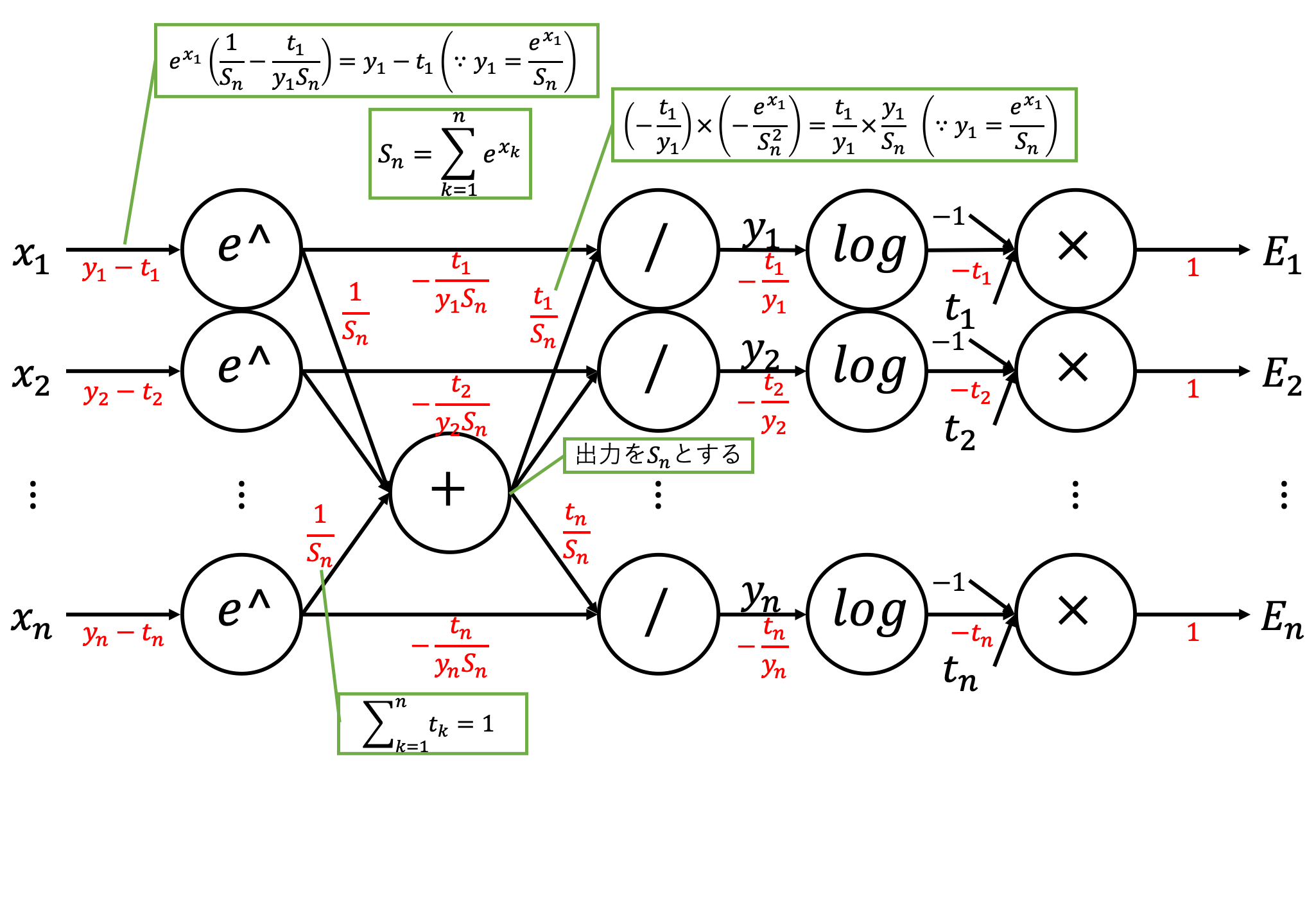
こんな感じですね。複雑怪奇です...
errors.py
class CrossEntropy(Error):
def forward(self, y, t, *args, **kwds):
self.error = - t*np.log(y)
return self.error
def backward(self, y, t, *args, **kwds):
return - t/y
損失関数のローカライズ
損失関数についてもローカライズしておきます。
errors.py
import numpy as np
class Error():
def __init__(self, *args, **kwds):
self.error = 0
def forward(self, *args, **kwds):
pass
def backward(self, *args, **kwds):
pass
def total_error(self, *args, **kwds):
return np.sum(self.error)/self.error.size
class SquareError(Error):
def forward(self, y, t, *args, **kwds):
self.error = 0.5 * (y - t)**2
return self.error
def backward(self, y, t, *args, **kwds):
return y - t
class BinaryCrossEntropy(Error):
def forward(self, y, t, *args, **kwds):
self.error = - t*np.log(y) - (1 - t)*np.log(1 - y)
return self.error
def backward(self, y, t, *args, **kwds):
return (y - t) / (y*(1 - y))
class CrossEntropy(Error):
def forward(self, y, t, *args, **kwds):
self.error = - t*np.log(y)
return self.error
def backward(self, y, t, *args, **kwds):
return - t/y
get_err.py
_err_dic = {"Square": SquareError,
"Binary": BinaryCrossEntropy,
"Cross": CrossEntropy,
}
def get_err(name, *args, **kwds):
if name in _err_dic.keys():
errfunc = _err_dic[name](*args, **kwds)
else:
raise ValueError(name, ": Unknown error function")
return errfunc
おわりに
いつか他の機械学習関連で使われる損失関数についてもまとめようかなぁ...
といってもその前に他の機械学習の手法とかについて勉強する必要があるか..