対象者
CNNを用いた画像認識で登場するim2col関数について詳しく知りたい方へ
初期の実装から改良版、バッチ・チャンネル対応版、ストライド・パディング対応版までgifや画像を用いて徹底解説します。
目次
col2imとは
col2im関数はim2col関数と対を成す、画像認識などの分野では欠かせない重要な関数です。
その役割はim2col関数の逆で、順伝播の際にim2col関数でテンソル$\rightarrow$行列に変換したのに対し、逆伝播の際にcol2im関数で行列$\rightarrow$テンソルに変換します。
こうすることでフィルタなどの学習に適した形状に変形します。
col2imの動作と初期の実装
まずは初期の実装から考えてみましょう。つまり
stride = 1 \\
pad = 0
であるとします。
動作はim2col関数の逆ですので下のようになります。
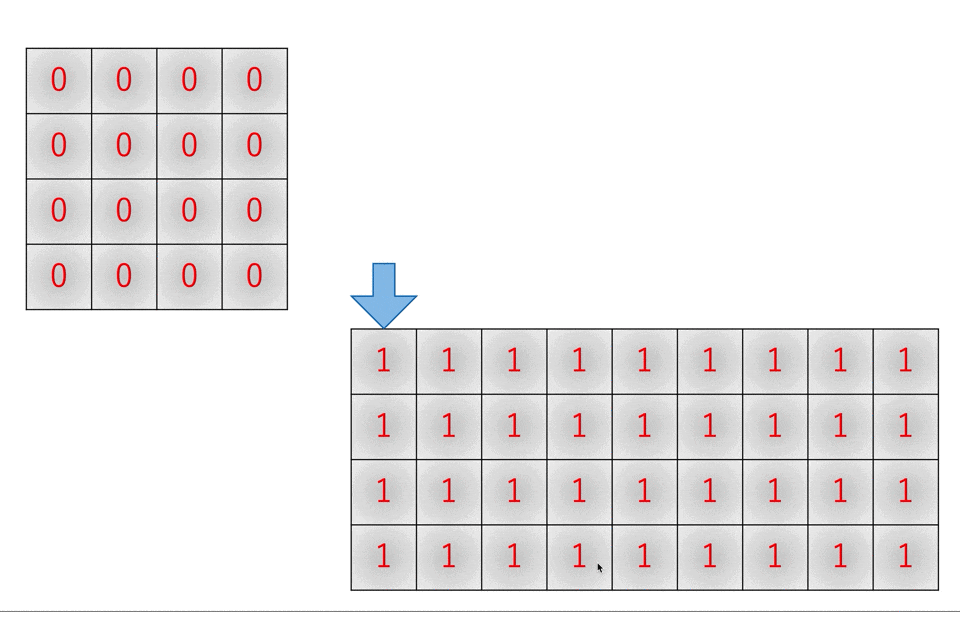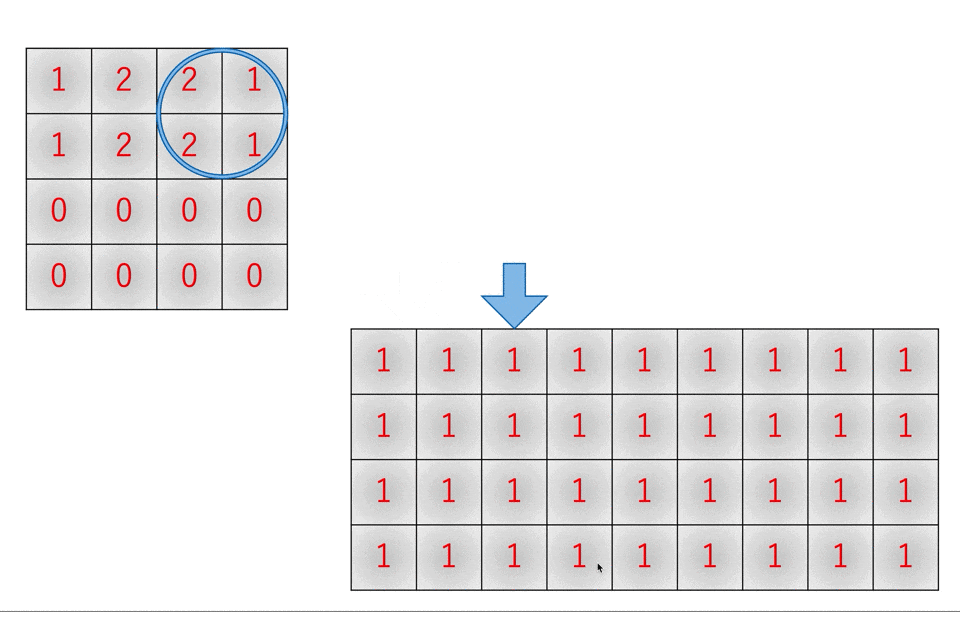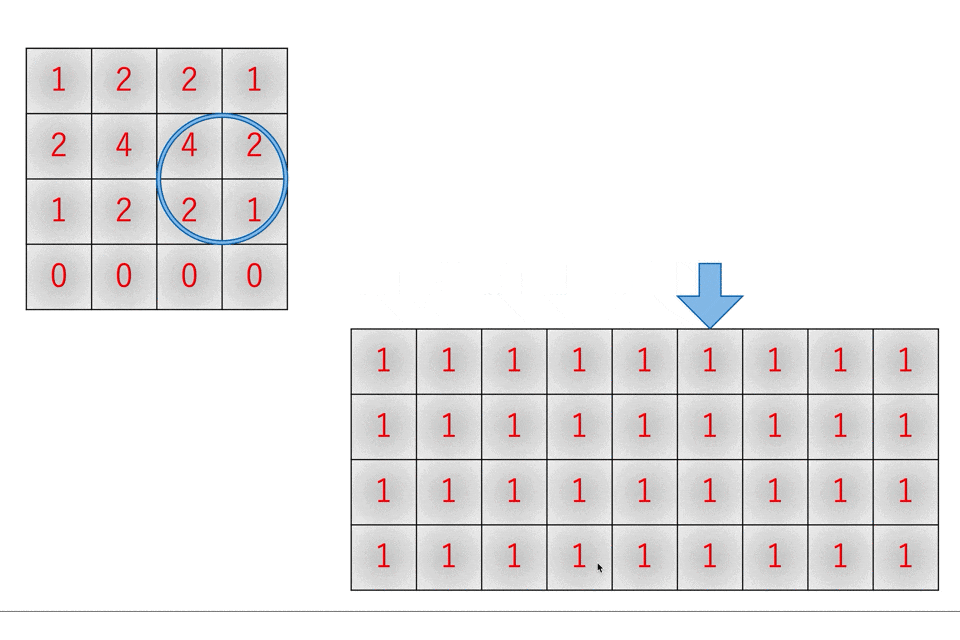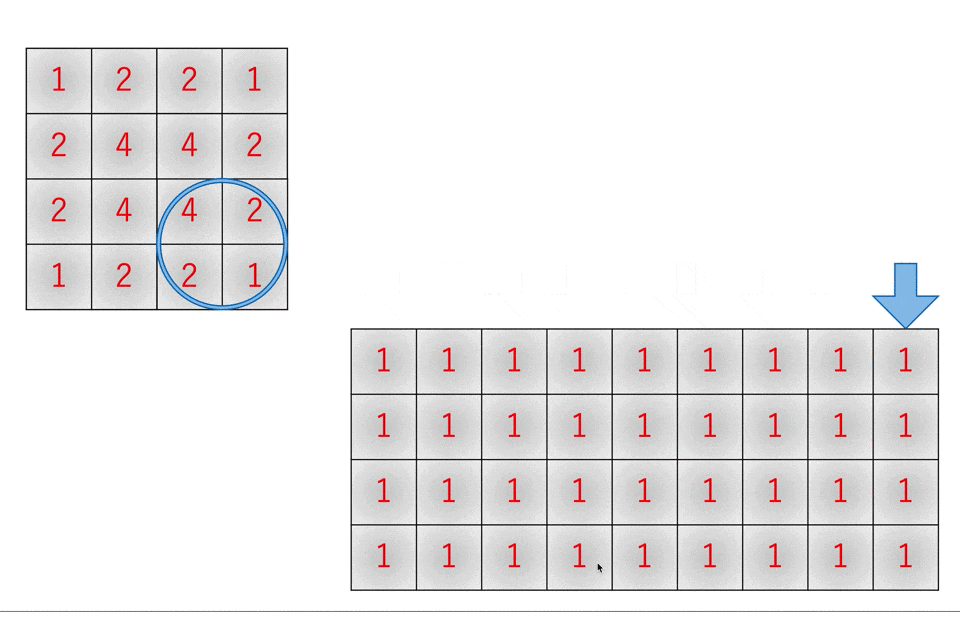
このとき、重なる部分は足し算することに注意してください。理由はフィルタリングの動作を考えると分かります。
ある要素に注目したとき、フィルタリングによって影響を受ける次層の要素は下の図のようになっています。
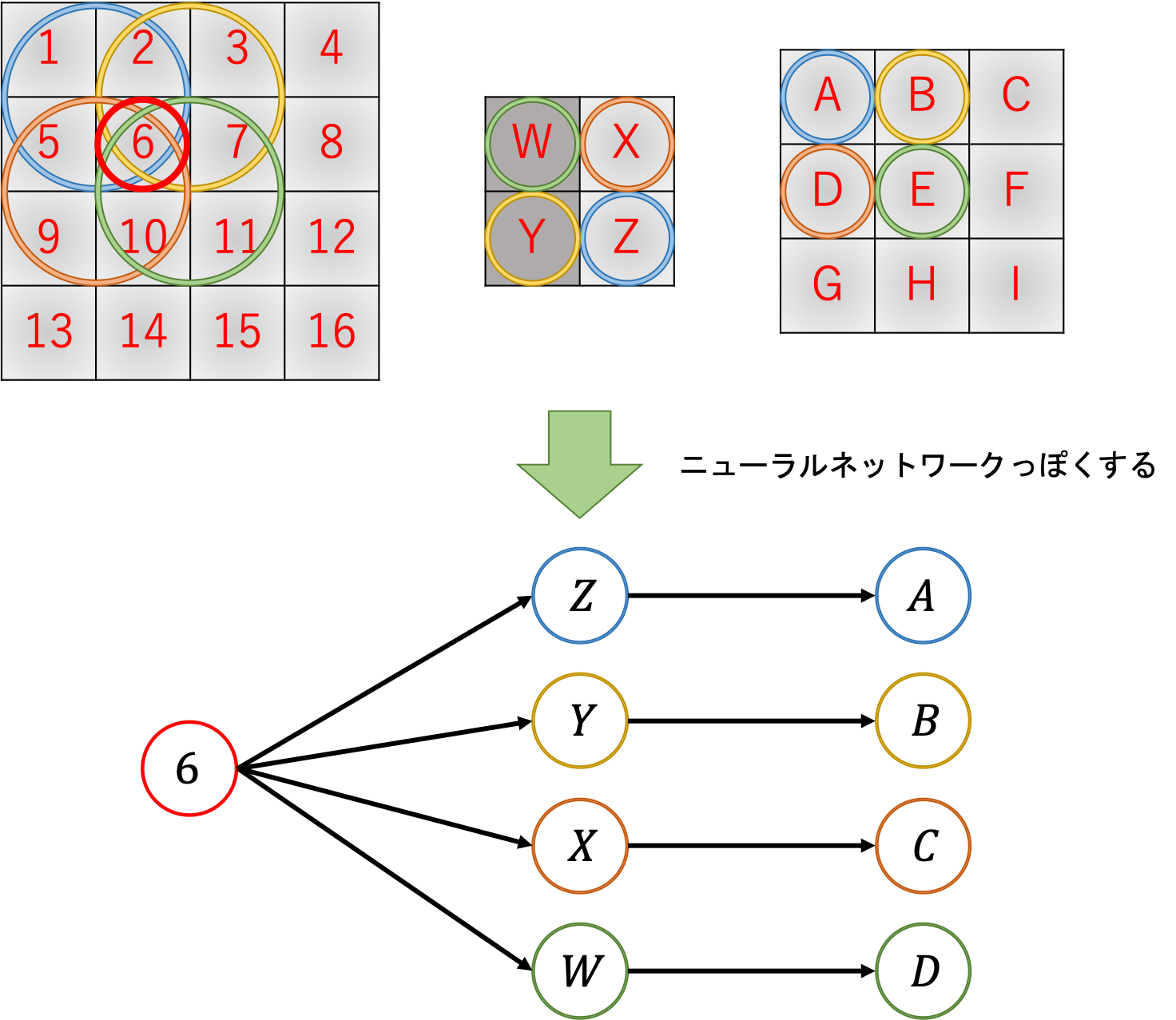
つまり、それぞれの要素に分岐して流れているわけですね。ということは逆伝播で流れてきた勾配は足し合わせなければなりません。
だからcol2im関数で変形する場合は「重なる部分は足し算する」必要があるんですね。
では、単純にこのロジックに従ってプログラムを組んでみましょう。
初期の`col2im`
def col2im(cols, I_shape, O_shape):
def get_f_shape(i, o):
return i - o + 1
I_h, I_w = I_shape
O_h, O_w = O_shape
F_h = get_f_shape(I_h, O_h)
F_w = get_f_shape(I_w, O_w)
images = np.zeros((I_h, I_w))
for h in range(O_h):
h_lim = h + F_h
for w in range(O_w):
w_lim = w + F_w
images[h:h_lim, w:w_lim] += cols[:, h*O_h+w].reshape(F_h, F_w)
return images
x = np.ones((4, 4))
f = np.arange(-2*2, 0).reshape(2, 2)
im2col_x, O_shape = im2col(x, f, pad=0, get_out_size=True)
im2col_f, Of_shape = im2col(f, f, get_out_size=True)
print(im2col_x)
print(im2col_f)
print(col2im(im2col_x, x.shape, O_shape))
print(col2im(im2col_f, f.shape, Of_shape))
こんな感じになります。まず変形後の形状になっている箱を用意して、そこに各列ごとに変形して放り込んでいます。
ここで、フィルタの形状はim2colの入力と出力とフィルタの関係式
O_h = I_h - F_h + 1 \\
O_w = I_w - F_w + 1
を利用して計算しています。
col2imの改良
やはり初期の実装ではim2col同様$O_h O_w$回のアクセスが必要となるため、処理速度が遅く実用的ではないという欠点があります。ということで、im2colの時と同様に工夫します。やり方はただの逆順ですね。
改良版`col2im`
def col2im(cols, I_shape, O_shape):
def get_f_shape(i, o):
return i - o + 1
I_h, I_w = I_shape
O_h, O_w = O_shape
F_h = get_f_shape(I_h, O_h)
F_w = get_f_shape(I_w, O_w)
cols = cols.reshape(F_h, F_w, O_h, O_w)
images = np.zeros((I_h, I_w))
for h in range(F_h):
h_lim = h + O_h
for w in range(F_w):
w_lim = w + O_w
images[h:h_lim, w:w_lim] += cols[h, w, :, :]
return images
x = np.ones((4, 4))
f = np.arange(-2*2, 0).reshape(2, 2)
im2col_x, O_shape = im2col(x, f, pad=0, get_out_size=True)
im2col_f, Of_shape = im2col(f, f, get_out_size=True)
print(im2col_x)
print(im2col_f)
print(col2im(im2col_x, x.shape, O_shape))
print(col2im(im2col_f, f.shape, Of_shape))
まずcol2imに入力される行列を

から

このような形状に変形します。改良版im2colでの出力行列のメモリ確保時と同じ形状です。
あとは
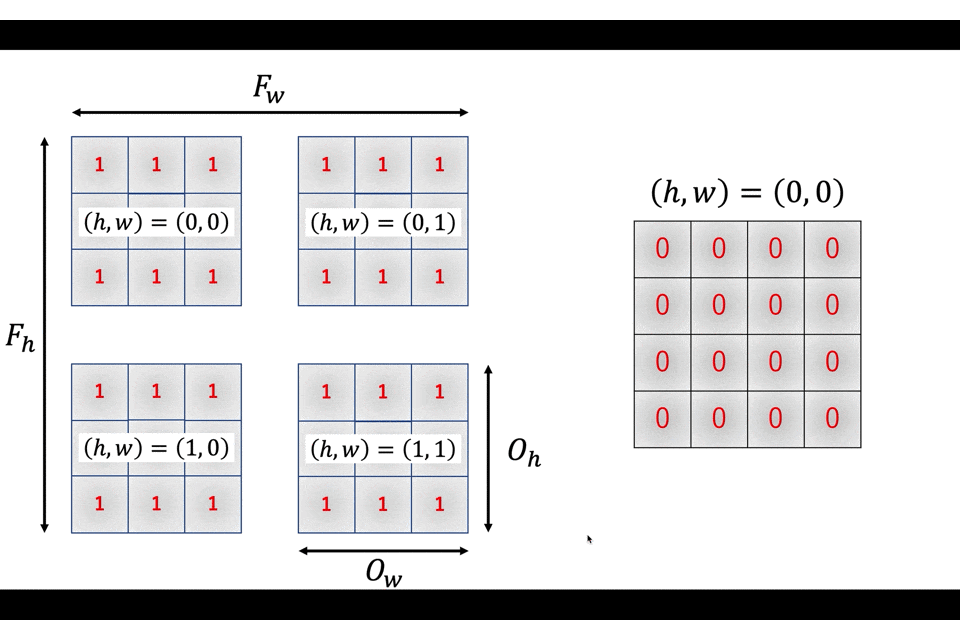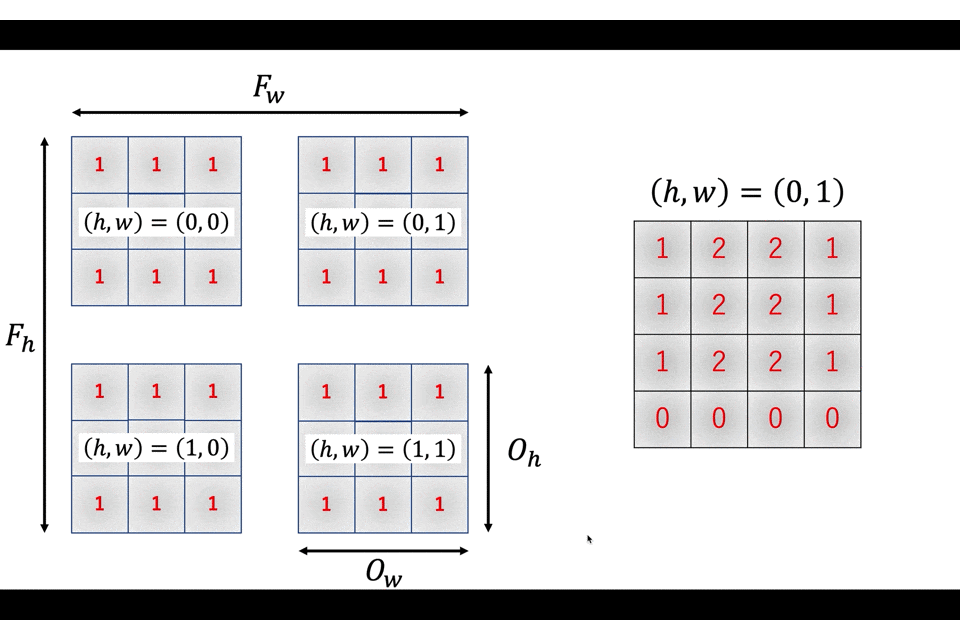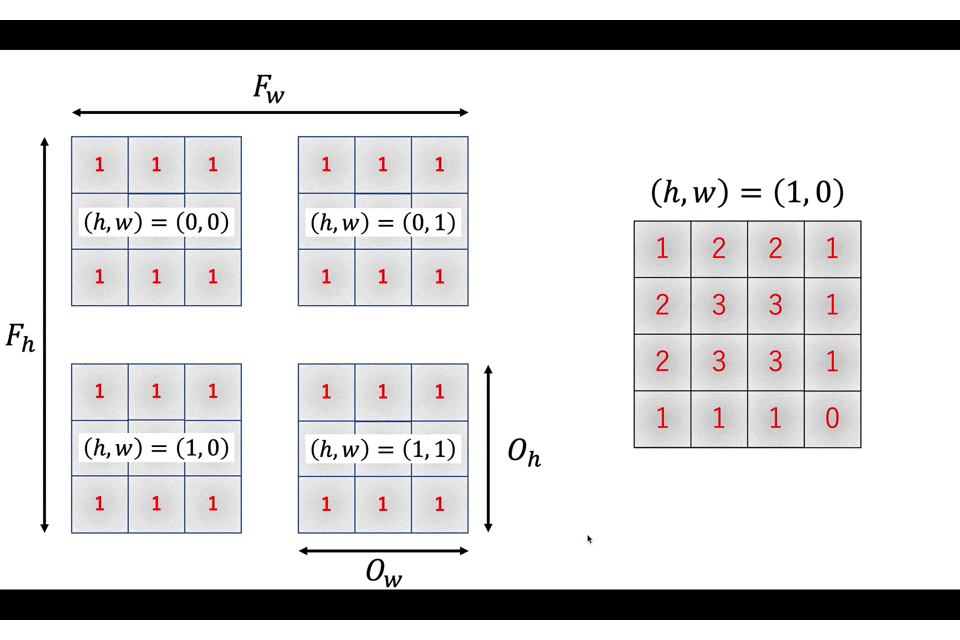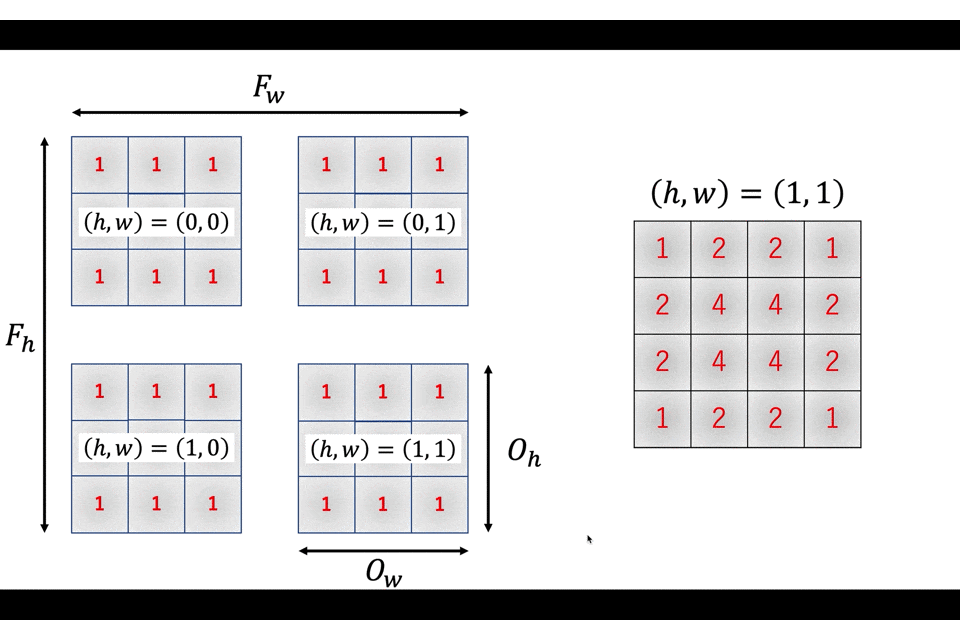
こんな感じでアクセスしていきます。テクニカルですね〜
完成版col2im
ということで最後にストライドとパディングを考慮します。
完成版`col2im`
import numpy as np
def col2im(cols, I_shape, O_shape, stride=1, pad=0):
def get_f_shape(i, o, s, p):
return int(i + 2*p - (o - 1)*s)
if len(I_shape) == 2:
B = C = 1
I_h, I_w = I_shape
elif len(img_shape) == 3:
C = 1
B, I_h, I_w = I_shape
else:
B, C, I_h, I_w = I_shape
O_h, O_w = O_shape
if isinstance(stride, tuple):
stride_ud, stride_lr = stride
else:
stride_ud = stride
stride_lr = stride
if isinstance(pad, tuple):
pad_ud, pad_lr = pad
elif isinstance(pad, int):
pad_ud = pad
pad_lr = pad
F_h = get_f_shape(I_h, O_h, stride_ud, pad_ud)
F_w = get_f_shape(I_w, O_w, stride_lr, pad_lr)
pad_ud = int(np.ceil(pad_ud))
pad_lr = int(np.ceil(pad_lr))
cols = cols.reshape(C, F_h, F_w, B, O_h, O_w).transpose(3, 0, 1, 2, 4, 5)
images = np.zeros((B, C, I_h+2*pad_ud+stride-1, I_w+2*pad_lr+stride-1))
for h in range(F_h):
h_lim = h + stride*O_h
for w in range(F_w):
w_lim = w + stride*O_w
images[:, :, h:h_lim:stride, w:w_lim:stride] += cols[:, :, h, w, :, :]
return images[:, :, pad_ud : I_h+pad_ud, pad_lr : I_w+pad_lr]
x = np.ones((4, 4))
f = np.arange(-2*2, 0).reshape(2, 2)
im2col_x, O_shape, x_pad = im2col(x, f, pad="same")
im2col_f, Of_shape, f_pad = im2col(f, f)
print(im2col_x)
print(im2col_f)
#print((im2col_f.T@im2col_x).reshape(*O_shape))
print(col2im(im2col_x, x.shape, O_shape, pad=x_pad))
print(col2im(im2col_f, f.shape, Of_shape, pad=f_pad))
ストライドとパディングを考慮した場合の形状計算は
O_h = \left\lceil \cfrac{I_h - F_h + 2\textrm{pad}_{ud}}{\textrm{stride}_{ud}} \right\rceil + 1 \\
O_w = \left\lceil \cfrac{I_w - F_w + 2\textrm{pad}_{lr}}{\textrm{stride}_{lr}} \right\rceil + 1 \\
なので、ここからフィルタの形状を計算します。
F_h = I_h + 2\textrm{pad}_{ud} - (O_h - 1) \textrm{stride}_{ud} \\
F_w = I_w + 2\textrm{pad}_{lr} - (O_w - 1) \textrm{stride}_{lr}
色々と考えていましたが、きちんと復元するには$\textrm{pad}_{ud}, \textrm{pad}_{lr}$の厳密な値(天井関数による切り上げ前の値)が必要っぽいので、im2col関数の実装もそれに合わせて変更しました。
ちょっとした疑問
実験していて気付いたのですが、$4 \times 4$行列の入力行列に上下左右$\textrm{pad} = 1$を追加すると$6 \times 6$となり、これに$2 \times 2$行列のフィルタを$\textrm{stride}=1$でかけると出力行列は$5 \times 5$になるはずなんですが、そうはなってないんですよね。
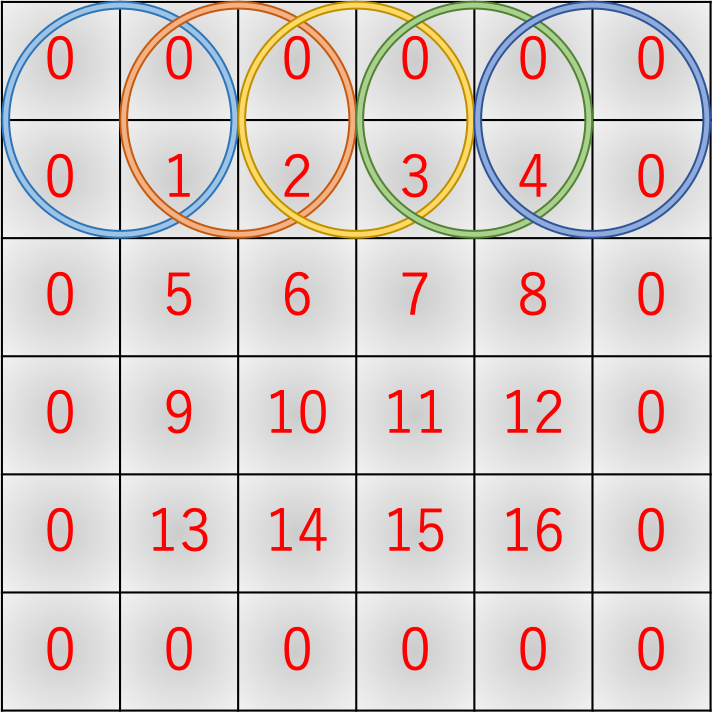
なんでかな〜と結構考えたんですが、そういえばこの条件でim2col関数に$\textrm{pad}=\textrm{same}$を入力すると計算結果のパディングが$\textrm{pad}=0.5$になるんですね。そしてもちろんパディング幅は整数ですので、仕様上切り上げて$\textrm{pad}=1$としているために$6 \times 6$行列になってしまっています。
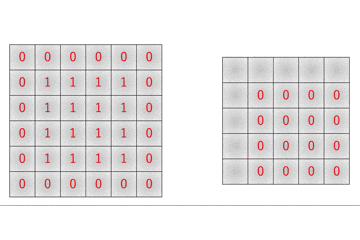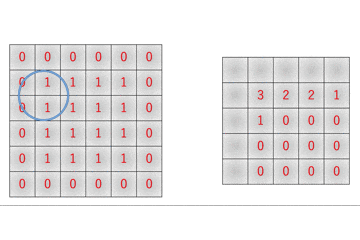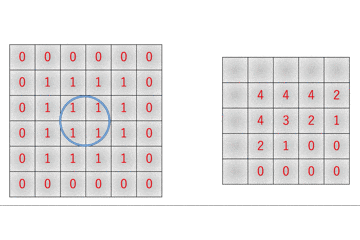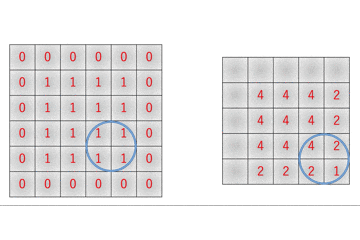
そのため本当は$5 \times 5$行列として扱うべきとなっており、実際にim2col関数では左上の$5 \times 5$行列のみを利用した物が返されているのがわかると思います。
その証拠に、col2im関数で重なる部分が

のように、左上部分が4回足し算されています。
おわりに
im2col関数とただの逆順であるため解説はかなり簡略化してあります。
もっと詳しい説明は時間ができたら追加していくかもしれません。