概要
前回の記事はこちら
前回記事で「KerasのMNISTデータセットで学習しようとすると数時間かかる」と書きました。MNISTデータセット程度の小さなデータセットでそんなにかかるのはやってられないので高速化します。
深層学習の高速化といえばGPUやTPUの利用ですね〜
ということで、本記事ではNVIDIA製のGPUを用いるためのGPUプログラミングをやっていきます。
使用するパッケージはCuPyにしました。理由は後ほど...
次回記事はこちら
目次
深層学習の高速化
注:だらだら喋るのでスキップしてもらって構いません
昨今のコンピュータアーキテクチャの発展は日進月歩どころではないレベルの速度で進んでいます。例えば私が子どもの頃はゲームボーイアドバンスが流行っていましたが、そこで動くゲームのデータ容量は最大でも32MBだったそうです。ところが今やPS4やPS5、Switchなんかのとんでもスペックなゲームハードで動くゲームで言えば、当たり前のように10数GBなんかのデータ容量があるそうです。GBはMBの1024倍ですから、たった10何年かで1000倍近くのデータ量を扱えるようになったことになります。このことからHDDやSSDといった記憶媒体の進歩具合が伺えますね。
もちろん扱うデータ容量が増えるならコンピュータが処理する命令も飛躍的に増大します。
CPUに求められる処理能力は尽きるところを知りませんが、CPUの発展はそれに応えるように「ムーアの法則」と呼ばれる経験則に則り18ヶ月(最近は24ヶ月)で倍になっていきました1。これはつまり15年でコンピュータの処理性能が1024倍になることを意味します。すごいことですね〜
しかしながら、先にも述べた通りCPUに求められる処理能力というのは、CPUが性能向上してできることが増えるたび青天井に求められます。そのため、いつの時代も性能不足が嘆かれてきました。
深層学習が脚光を浴びた背景には間違いなくCPUの性能向上があり、またそのためにCPUの性能不足が嘆かれる場面が多くあります。その一つが画像認識及び畳み込みニューラルネットワーク(CNN)です。
画像データは2次元ですので、ちょっと大きな画像データセットを学習に使おうとするとあっという間に万単位以上の要素を持つテンソルになってしまい、現行のCPUでは圧倒的に性能不足です。
前回の記事では具体的に述べていませんが、実験したところ、KerasのMNISTデータセットを用いて学習しようとすると、google colaboratory上で1エポック30分もかかります。google colaboratoryは12時間制限があるので(外部に途中経過一時保存&再読み込みからの学習再開をしなければ)24エポックしか学習できません。まあそれでもMNISTデータセットくらいなら十分な精度の学習ができますが。
とにかく、これでは気軽に実験することもできません。そこで注目されたのがGPUです。
GPU
CPUがCentral Processing Unit:中央処理装置であるのに対し、GPUはGraphics Processing Unit:グラフィック処理装置と呼ばれます。名前の通り、画面描画のための計算に特化した半導体プロセッサです。
CPUは汎用計算に優れているのに対して、GPUは画像処理のための計算に特化している分その速度は圧倒的です。数千個以上のコアで超並列計算を行うため、画面描画は基本的にラグなく行われます。
そしてここがミソなのですが、この超並列計算と行列計算には親和性があります。
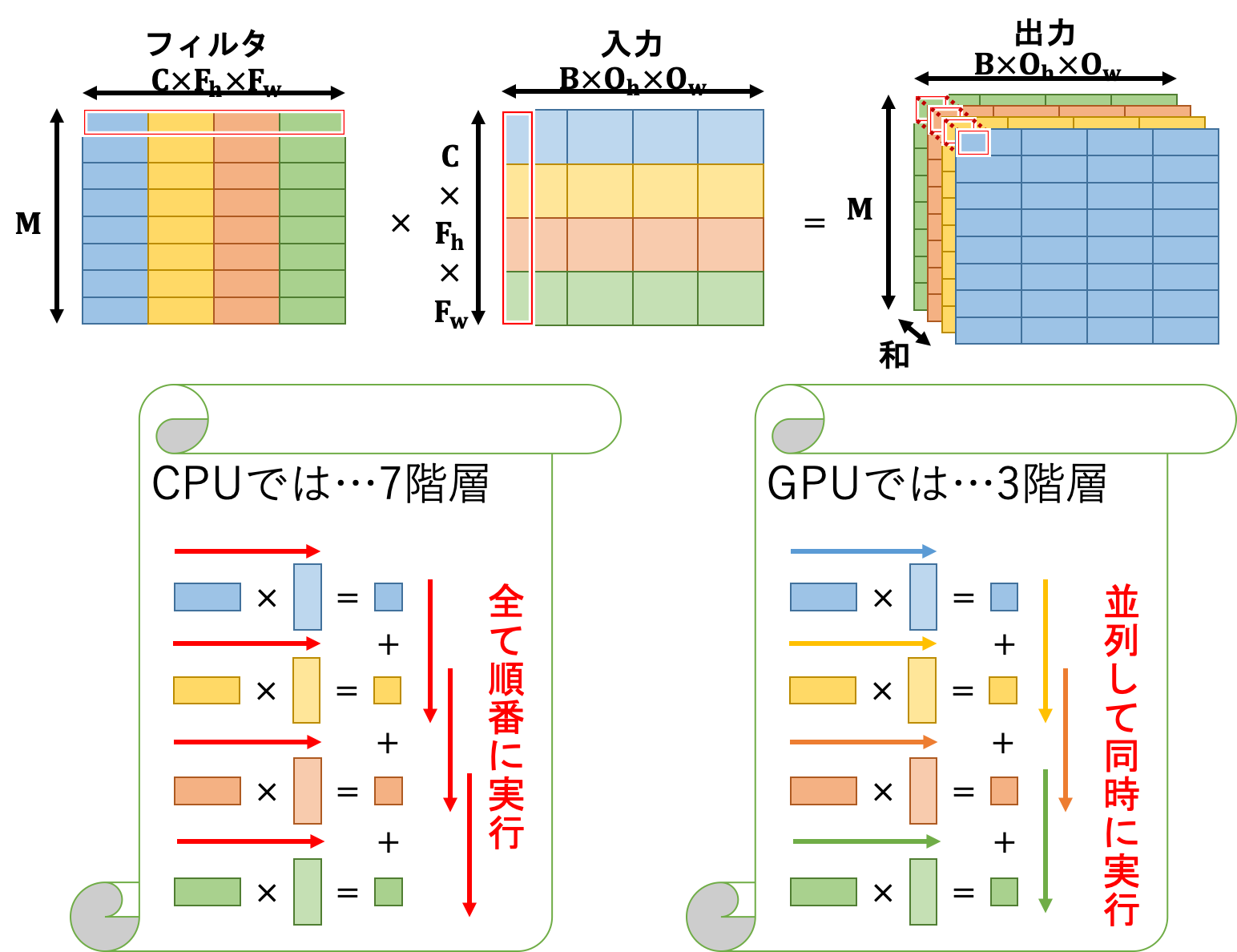
この図はただの喩えというか、実際にGPU上でこのような処理が行われているということではありませんので注意してください。この図から読み取って欲しいことは、行列計算は並列実行できるというただ1点のみです。
ちなみに上図はCPUの並列化でも実現できますが、GPUは規模が桁違いなのです。
そんなこんなで、深層学習に目をつけられたGPUはGPGPU: General-Purpose computing on Graphics Processing Units: グラフィック処理装置を汎用計算に用いる技術などの登場を経てその発展に多大な貢献をします。
TPU
さて、GPU及びGPGPUの登場で深層学習は急速な発展を遂げましたが、それで飽き足りないのが人間の性ですね。ということで登場したのがTPU: Tensor Processing Unit: テンソル処理装置です。
GPUはあくまでグラフィック用に設計されていたものですが、そこからさらに深層学習のための高速テンソル計算を実現するために設計されたのがTPUです。汎用性と少しばかりの演算精度を犠牲に、GPUをも圧倒する、どころか足元にすら及ばないような高速化を成し遂げました。
テンソル計算に特化しているためGPUよりもさらに汎用性が落ち、また通常は32bitや64bitで計算されるところを8bitや16bitに落とすことで高速化しています。
さらに、キャッシュメモリへの書き込みすらも減らすために演算回路内でデータやり取りを行うなど、とにかく高速にテンソル計算ができるような工夫がなされています。
その圧倒的な威力を示す代表例がAlphaGo Zeroです。単純計算でCPU換算すると2万年くらいかかる量の計算を、複数のTPUなどを用いて3日で済ませてしまいました。意味がわかりませんね。笑
そんなこんなで、超並列計算が深層学習に及ぼす恩恵は非常に大きなものとなっています。
CuPyによるGPUプログラミング
さて、本題に入ります。本記事ではCuPyを用いてGPUプログラミングを行います。
CuPyは元々ChainerでのGPUプログラム実装(CUDAプログラミング)のために開発されたパッケージだったそうです。
最大の利点はnumpyを踏襲しているため、ほとんどのコードでnp(import numpy as np)をcp(import cupy as cp)と書き換えるだけで動くことです。これが本記事でCuPyを利用することにした理由です。簡単って素晴らしい!笑
ぶっちゃけほとんど考えることはありません。というかプロトタイプとして実装したので汚いです...いずれ整理していきます。デコレータとか使うといいのかなぁ...いいアイデアあればぜひ教えてください。
コードはこちらです。
ちなみに、google colaboratoryでGPUを利用するには、ランタイムのタイプにGPUを選択する必要があります。
CuPyのインストールと確認
CuPyのインストールは以下のコードを入力したセルを実行します。
!curl https://colab.chainer.org/install | sh -
% Total % Received % Xferd Average Speed Time Time Time Current
Dload Upload Total Spent Left Speed
100 1580 100 1580 0 0 6666 0 --:--:-- --:--:-- --:--:-- 6666
+ apt -y -q install cuda-libraries-dev-10-0
Reading package lists...
Building dependency tree...
Reading state information...
cuda-libraries-dev-10-0 is already the newest version (10.0.130-1).
0 upgraded, 0 newly installed, 0 to remove and 11 not upgraded.
+ pip install -q cupy-cuda100 chainer
|████████████████████████████████| 348.0MB 51kB/s
+ set +ex
Installation succeeded!
これで自動的に必要なバージョンのCuPyがインストールされます。ついでにChainerも。使いませんがまあいいでしょう。
以下のコードできちんとインストールされているか確認できます。
!python -c 'import chainer; chainer.print_runtime_info()'
Platform: Linux-4.19.112+-x86_64-with-Ubuntu-18.04-bionic
Chainer: 7.4.0
ChainerX: Not Available
NumPy: 1.18.5
CuPy: Not Available
iDeep: 2.0.0.post3
こんな感じの出力が確認できればOKです。
CuPyプログラミング
例として活性化関数(の一部)を挙げておきます。
import numpy as np
import cupy as cp
class Activator():
def __init__(self, *args, mode="cpu", **kwds):
self.mode = mode
if self.mode == "cpu":
self.forward = self.cpu_forward
self.backward = self.cpu_backward
self.update = self.cpu_update
elif self.mode == "gpu":
self.forward = self.gpu_forward
self.backward = self.gpu_backward
self.update = self.gpu_update
def cpu_forward(self, *args, **kwds):
raise NotImplemented
def gpu_forward(self, *args, **kwds):
raise NotImplemented
def cpu_backward(self, *args, **kwds):
raise NotImplemented
def gpu_backward(self, *args, **kwds):
raise NotImplemented
def cpu_update(self, *args, **kwds):
raise NotImplemented
def gpu_update(self, *args, **kwds):
raise NotImplemented
class step(Activator):
def cpu_forward(self, x, *args, **kwds):
return np.where(x > 0, 1, 0)
def gpu_forward(self, x, *args, **kwds):
return cp.where(x > 0, 1, 0)
def cpu_backward(self, x, *args, **kwds):
return np.zeros_like(x)
def gpu_backward(self, x, *args, **kwds):
return cp.zeros_like(x)
脳死で書いてます。なんかこう、もっとスマートなやり方があるはず...
やっていることとしては、Pythonが関数をある種のオブジェクトとして代入できることを利用して分岐させています。
関数の実装の部分も、npとcpが違うだけですね!これがCuPyのいいところです。お手軽便利にGPUプログラミングができますね〜
効果の確認
ではKerasのMNISTデータセットで実験してみましょう。実行は実験コードまでの全てのセルを実行し、Kerasのデータを読み込むセルを実行、最後にCNN実験コード本体を実行します。
%matplotlib inline
# 畳み込み層と出力層を作成
M, F_h, F_w = 10, 3, 3
lm = LayerManager((x_train, x_test), (t_train, t_test), mode="gpu")
#lm.append(name="c", I_shape=(C, I_h, I_w), F_shape=(M, F_h, F_w), pad=1,
# wb_width=0.1, opt="AdaDelta", opt_dic={"eta": 1e-2})
lm.append(name="c", I_shape=(C, I_h, I_w), F_shape=(M, F_h, F_w), pad=1)
lm.append(name="p", I_shape=lm[-1].O_shape, pool=2)
#lm.append(name="m", n=100, wb_width=0.1,
# opt="AdaDelta", opt_dic={"eta": 1e-2})
lm.append(name="m", n=100)
#lm.append(name="o", n=n_class, act="softmax", err_func="Cross", wb_width=0.1,
# opt="AdaDelta", opt_dic={"eta": 1e-2})
lm.append(name="o", n=n_class, act="softmax", err_func="Cross")
# 学習させる
epoch = 5
threshold = 1e-8
n_batch = 8
lm.training(epoch, threshold=threshold, n_batch=n_batch, show_train_error=True)
# 予測する
print("training dataset")
_ = lm.predict(x=lm.x_train, y=lm.y_train)
print("test dataset")
if lm.mode == "cpu":
y_pred = lm.predict()
elif lm.mode == "gpu":
y_pred = lm.predict().get()
progress:[XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX]483s/514s
training dataset
correct: [5 0 4 1 9 2 1 3 1 4 3 5 3 6 1 7]
predict: [5 0 4 1 9 2 1 3 1 4 3 5 3 6 1 7]
accuracy rate: 98.58 % (59148/60000)
test dataset
correct: [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5]
predict: [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5]
accuracy rate: 97.58 % (9758/10000)
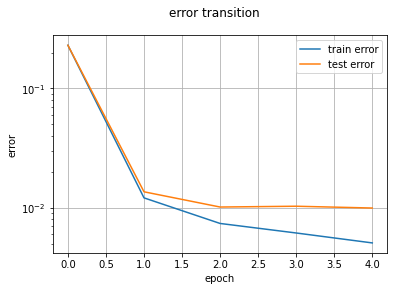
特に意味はありませんが、活性化関数や重みレンジwb_width、最適化子などをデフォルトにしています。つまり活性化関数はReLU、wb_widthは0.05、最適化子はAdamとなっています。学習エポックは5に設定しています。
実行結果は、1エポックあたり約100秒ですね!実に18倍の高速化に成功しました。まだまだ遅いですが、まあ実用には耐えられるでしょう。MNIST以外は...(遠い目)
さらなる高速化に向けて
ところで、テストコードの一番下にはKerasでのMNISTデータセット学習コードを載せてあります。
こちらからコピペしました。
mnist_cnn.py
'''Trains a simple convnet on the MNIST dataset.
Gets to 99.25% test accuracy after 12 epochs
(there is still a lot of margin for parameter tuning).
16 seconds per epoch on a GRID K520 GPU.
'''
from __future__ import print_function
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
batch_size = 128
num_classes = 10
epochs = 12
# input image dimensions
img_rows, img_cols = 28, 28
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
x_train shape: (60000, 28, 28, 1)
60000 train samples
10000 test samples
Epoch 1/12
469/469 [==============================] - 4s 9ms/step - loss: 2.2889 - accuracy: 0.1426 - val_loss: 2.2611 - val_accuracy: 0.2889
Epoch 2/12
469/469 [==============================] - 4s 9ms/step - loss: 2.2432 - accuracy: 0.2350 - val_loss: 2.2046 - val_accuracy: 0.4885
Epoch 3/12
469/469 [==============================] - 4s 9ms/step - loss: 2.1837 - accuracy: 0.3312 - val_loss: 2.1279 - val_accuracy: 0.5908
Epoch 4/12
469/469 [==============================] - 4s 9ms/step - loss: 2.1039 - accuracy: 0.4035 - val_loss: 2.0235 - val_accuracy: 0.6492
Epoch 5/12
469/469 [==============================] - 4s 9ms/step - loss: 1.9959 - accuracy: 0.4669 - val_loss: 1.8864 - val_accuracy: 0.6989
Epoch 6/12
469/469 [==============================] - 4s 9ms/step - loss: 1.8604 - accuracy: 0.5193 - val_loss: 1.7149 - val_accuracy: 0.7420
Epoch 7/12
469/469 [==============================] - 4s 9ms/step - loss: 1.6990 - accuracy: 0.5681 - val_loss: 1.5179 - val_accuracy: 0.7688
Epoch 8/12
469/469 [==============================] - 4s 9ms/step - loss: 1.5315 - accuracy: 0.6014 - val_loss: 1.3180 - val_accuracy: 0.7912
Epoch 9/12
469/469 [==============================] - 4s 9ms/step - loss: 1.3717 - accuracy: 0.6327 - val_loss: 1.1394 - val_accuracy: 0.8029
Epoch 10/12
469/469 [==============================] - 4s 9ms/step - loss: 1.2431 - accuracy: 0.6562 - val_loss: 0.9945 - val_accuracy: 0.8171
Epoch 11/12
469/469 [==============================] - 4s 9ms/step - loss: 1.1369 - accuracy: 0.6757 - val_loss: 0.8818 - val_accuracy: 0.8263
Epoch 12/12
469/469 [==============================] - 4s 9ms/step - loss: 1.0520 - accuracy: 0.6957 - val_loss: 0.7949 - val_accuracy: 0.8356
Test loss: 0.7948545217514038
Test accuracy: 0.8356000185012817
は、速い...さらに20倍も高速ですね...ということはまだまだ高速化の余地が残されているということですね!
では現状のぼくのコードで計算速度のボトルネックはどこなのかを調べてみます。
処理時間の計測はtimeitマジックを利用しています。これを使うとうまいこと処理時間を計測してくれます。
誤差計算の時間計測
まずは誤差計算にかかる時間を計測してみます。
# 訓練誤差の計算
%%timeit
lm.forward(lm.x_train)
error = lm[-1].get_error(lm.y_train)
#----------output----------
# 1 loop, best of 3: 957 ms per loop
#--------------------------
# テスト誤差の計算
%%timeit
lm.forward(lm.x_test)
error = lm[-1].get_error(lm.y_test)
#----------output----------
# 10 loops, best of 3: 160 ms per loop
#--------------------------
訓練データの誤差計算はデータ量が60000ですので、まあこんなものでしょう。ていうかもっと少なくていいのでは...ここは改良できそうですね。テストデータと同じく10000個に減らせば1エポックあたり約0.8秒の短縮になりそうです。まあそれこそ誤差みたいなものですが。
全体(1エポックあたり100秒)から考えると、誤差計算が占める割合は総じて1%程度なので、ここはボトルネックではないでしょう。ということは学習部分が問題そうですね。
学習部分の時間計測
学習部分の処理時間を計測していきます。1エポックあたりの処理時間のうち99%を占めているのが学習のどこかにあるはず...
# ミニバッチ1つ分のデータを計測対象とする。
rand_index = np.arange(lm.x_train.get().shape[0])
np.random.shuffle(rand_index)
rand = rand_index[0 : n_batch]
# 順伝播の計算
%%timeit
lm.forward(lm.x_train[rand])
#----------output----------
# 1000 loops, best of 3: 1.32 ms per loop
#--------------------------
# 逆伝播の計算
%%timeit
lm.backward(lm.y_train[rand])
#----------output----------
# 100 loops, best of 3: 10.3 ms per loop
#--------------------------
# 重み更新計算
%%timeit
lm.update()
#----------output----------
# 1000 loops, best of 3: 1.64 ms per loop
#--------------------------
明らかに逆伝播だけ異常に時間がかかっていますね。順伝播と重み更新に対して10倍かかっています。
今回学習データは60000個で、ミニバッチサイズが8なので、この計算過程が7500回繰り返されることになりますから、トータルで $(1.32+10.3+1.64) \times 7500 \times 10^{-3} = 23.92s$かかることになります。あれ、思ったより少ない...?十分時間かかっていますが、それでもなんか足りないですね...まあ結構振れ幅ありますし、とりあえずは気にしないでおきましょう。
ただの計算ミスでした...電卓の仕様はちゃんと理解しないとですね汗
$(1.32+10.3+1.64) \times 7500 \times 10^{-3} = 99.45s$
とにかく、逆伝播が異常に遅いので、さらに細かく計測していきます。
逆伝播の時間計測
ということで、逆伝播の処理を分割して計測していきます。
# 事前準備
err3 = lm[3].backward(lm.y_train[rand])
err2 = lm[2].backward(err3)
err2 = err2.reshape(n_batch, *lm[1].O_shape)
err1 = lm[1].backward(err2)
err0 = lm[0].backward(err1)
# 出力層の逆伝播
%%timeit
err3 = lm[3].backward(lm.y_train[rand])
#----------output----------
# 10000 loops, best of 3: 152 µs per loop
#--------------------------
# 中間層の逆伝播
%%timeit
err2 = lm[2].backward(err3)
err2 = err2.reshape(n_batch, *lm[1].O_shape)
#----------output----------
# 1000 loops, best of 3: 224 µs per loop
#--------------------------
# プーリング層の逆伝播
%%timeit
err1 = lm[1].backward(err2)
#----------output----------
# 1000 loops, best of 3: 9.72 ms per loop
#--------------------------
# 畳み込み層の逆伝播
%%timeit
err0 = lm[0].backward(err1)
#----------output----------
# 1000 loops, best of 3: 442 µs per loop
#--------------------------
プーリング層が桁違いに遅いことがわかりました。逆伝播の計算時間に占めるプーリング層の処理時間は約93.6%にもなります。ちなみにこちらは足すと大体10msちょっとになりますので、大体一致していますね。
プーリング層の逆伝播の時間計測
ということで、問題のプーリング層の逆伝播をさらに細かくみていきます。
# 事前準備
B, C, O_h, O_w = n_batch, *lm[1].O_shape
grad = err2.transpose(0, 2, 3, 1).reshape(-1, 1)
grad_x = cp.zeros((grad.size, lm[1].pool*lm[1].pool))
grad_x1 = grad_x.copy()
grad_x1[:, lm[1].max_index] = grad
grad_x2 = grad_x1.reshape(B*O_h*O_w, C*lm[1].pool*lm[1].pool).T
# 誤差の次元入れ替えと変形
%%timeit
grad = err2.transpose(0, 2, 3, 1).reshape(-1, 1)
#----------output----------
# 100000 loops, best of 3: 17.1 µs per loop
#--------------------------
# 空の行列生成
%%timeit
grad_x = cp.zeros((grad.size, lm[1].pool*lm[1].pool))
#----------output----------
# 100000 loops, best of 3: 7.89 µs per loop
#--------------------------
# 値埋め
%%timeit
grad_x1[:, lm[1].max_index] = grad
#----------output----------
# 1000 loops, best of 3: 9.5 ms per loop
#--------------------------
# 変形と転置
%%timeit
grad_x2 = grad_x1.reshape(B*O_h*O_w, C*lm[1].pool*lm[1].pool).T
#----------output----------
# 1000000 loops, best of 3: 1.86 µs per loop
#--------------------------
# col2im
%%timeit
grad_x3 = lm[1].col2im(grad_x2, (n_batch, *lm[1].I_shape), lm[1].O_shape,
stride=lm[1].pool, pad=lm[1].pad_state)
#----------output----------
# 10000 loops, best of 3: 112 µs per loop
#--------------------------
値埋めが他より圧倒的に遅いですね...ということはここがボトルネックなわけです。値埋めがプーリング層の逆伝播に占める割合は実に約98.6%となっています。
GPUは単純な計算には強いですが、こういったちょっと複雑な処理になると一気に遅くなってしまい、せっかくの性能をうまく活かし切ることができなくなります。
ということで改善案を考えてみます。
プーリング層の高速化
高速化にあたり、値埋めのうまい方法はないかなぁと考えてみました。
まず考えたのは、こういう複雑な処理はCPUの方が向いているのでGPUではなくCPUで処理することです。しかしながら、全体をCPUで処理したときのボトルネックもやはり同じ部分にあることが実験でわかったので、この案はボツとなりました。
続いて考えたのは、この部分の処理を別の形に書き換えることです。つまり「この代入処理をGPUが得意な計算処理で代替しよう」と考えました。
ということはインデックスを保持するのではなく、入力(をim2col関数に投げたもの)と同じ形状をした疎行列を保持すればいいわけですね。最大値に対応する場所だけ1、それ以外は0です。
必要なメモリ量は通常の$pool^2$倍になりますが、$pool$は大抵小さいのでいいでしょう。
import numpy as np
import cupy as cp
class PoolingLayer(BaseLayer):
def __init__(self, *, mode="cpu",
I_shape=None, pool=1, pad=0,
name="", **kwds):
self.mode = mode
self.name = name
if I_shape is None:
raise KeyError("Input shape is None.")
if len(I_shape) == 2:
C, I_h, I_w = 1, *I_shape
else:
C, I_h, I_w = I_shape
self.I_shape = (C, I_h, I_w)
# im2col関数とcol2im関数を保持
if self.mode == "cpu":
self.im2col = cpu_im2col
self.col2im = cpu_col2im
elif self.mode == "gpu":
self.im2col = gpu_im2col
self.col2im = gpu_col2im
if self.mode == "cpu":
_, O_shape, self.pad_state = self.im2col(
np.zeros((1, *self.I_shape)),
(pool, pool),
stride=pool, pad=pad)
elif self.mode == "gpu":
_, O_shape, self.pad_state = self.im2col(
cp.zeros((1, *self.I_shape)),
(pool, pool),
stride=pool, pad=pad)
self.O_shape = (C, *O_shape)
self.n = np.prod(self.O_shape)
self.pool = pool
self.F_shape = (pool, pool)
def forward(self, x):
B = x.shape[0]
C, O_h, O_w = self.O_shape
self.x, _, self.pad_state = self.im2col(x, self.F_shape,
stride=self.pool,
pad=self.pad_state)
self.x = self.x.T.reshape(B*O_h*O_w*C, -1)
if self.mode == "cpu":
#self.max_index = np.argmax(self.x, axis=1)
self.y = np.max(self.x, axis=1, keepdims=True)
self.max_index = np.where(self.y == self.x, 1, 0)
self.y = self.y.reshape(B, O_h, O_w, C).transpose(0, 3, 1, 2)
elif self.mode == "gpu":
#self.max_index = cp.argmax(self.x, axis=1)
self.y = cp.max(self.x, axis=1, keepdims=True)
self.max_index = cp.where(self.y == self.x, 1, 0)
self.y = self.y.reshape(B, O_h, O_w, C).transpose(0, 3, 1, 2)
return self.y
def backward(self, grad):
B = grad.shape[0]
I_shape = B, *self.I_shape
C, O_h, O_w = self.O_shape
grad = grad.transpose(0, 2, 3, 1).reshape(-1, 1)
if self.mode == "cpu":
self.grad_x = np.zeros((grad.size, self.pool*self.pool))
elif self.mode == "gpu":
self.grad_x = cp.zeros((grad.size, self.pool*self.pool))
#self.grad_x[:, self.max_index] = grad
self.grad_x = self.max_index*grad
self.grad_x = self.grad_x.reshape(B*O_h*O_w, C*self.pool*self.pool).T
self.grad_x = self.col2im(self.grad_x, I_shape, self.O_shape,
stride=self.pool, pad=self.pad_state)
return self.grad_x
def update(self, **kwds):
pass
では実験してみましょう。
# プーリング層の逆伝播
%%timeit
err1 = lm[1].backward(err2)
#----------output----------
# 1000 loops, best of 3: 280 µs per loop
#--------------------------
# 値埋め
%%timeit
grad_x1 = lm[1].max_index*grad
#----------output----------
# 100000 loops, best of 3: 16.3 µs per loop
#--------------------------
ちなみに上記の結果は以前の実験結果とは異なるGPUにアサインされているものだと考えられますので、一概にその結果を比べていいかは微妙ですが、とりあえず高速化することには成功していることは間違い無いでしょう。こうなると今度はcol2im関数などが問題になってきますので、そのあたりにまだまだ高速化の余地がありますね。
また、全体としても
progress:[XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX]287s/285s
training dataset
correct: [5 0 4 1 9 2 1 3 1 4 3 5 3 6 1 7]
predict: [5 0 4 1 9 2 1 3 1 4 3 5 3 6 1 7]
accuracy rate: 99.21333333333334 % (59528/60000)
test dataset
correct: [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5]
predict: [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5]
accuracy rate: 98.03 % (9803/10000)
このように、1エポックあたり50s程度に短縮することができました!
また、1ミニバッチあたりの学習時間が6msくらいなので、1エポックあたりの学習時間は$6\times 7500 \times 10^{-3} = 45s$となっています。おり、先のミスマッチも解消されています...結局何だったんでしょう。同じGPUへのアサイン中に実験したはずなんですが...まあいいでしょう。
おわりに
こんな感じでボトルネック部分を探して改善、高速化していきます。今後も随時改良していきます。
P.S. ミニバッチサイズを128にするとKerasでの実験とほとんど同じような実行時間となりました。よかったよかった。
深層学習シリーズ
- 深層学習入門 ~基礎編~
- 深層学習入門 ~コーディング準備編~
- 深層学習入門 ~順伝播編~
- 深層学習入門 ~逆伝播編~
- 深層学習入門 ~学習則編~
- 深層学習入門 ~ローカライズと損失関数編~
- 深層学習入門 ~関数近似編~
- 深層学習入門 ~畳み込みとプーリング編~
- 深層学習入門 ~CNN実験編~
- 深層学習外伝 ~GPUプログラミング編~
- 深層学習入門 ~ドロップアウト編~
- 活性化関数一覧 (2020)
- 勾配降下法一覧 (2020)
- 見てわかる!最適化手法の比較 (2020)
- im2col徹底理解
- col2im徹底理解
- numpy.pad関数完全理解
-
厳密には「半導体の集積率が18ヶ月(24ヶ月)で倍になる」です。 ↩