対象者
前回の記事はこちら
前回まででDNN(Deep Neural Network)は完成です。
(レイヤーマネージャの使い方も含めて別の記事でDNNで遊ぶ予定です)
ここでは画像認識へ向けてCNN(Convolutional Neural Network)を作成していきます。
ここで用いるim2col関数とcol2im関数は、こちらとこちらで紹介しています。
次回の記事はこちら
目次
畳み込み層
画像認識に多大な恩恵を与えるのが畳み込みという処理です。導入としては、画像などの位置関係が重要だと思われるデータに対して、単純にニューラルネットワークに1次元に平滑化して流すのはせっかくの位置関係という重要な情報を捨てるようなものなのでもったいない、みたいな感じです。
入力の次元を維持したまま、つまり位置関係などの重要な情報を維持したままニューラルネットワークにデータを流すのが畳み込み層の役割です。
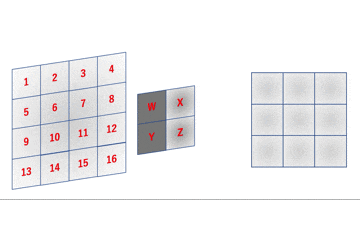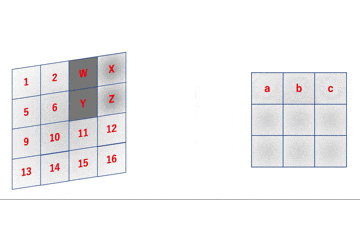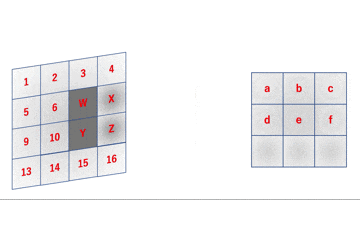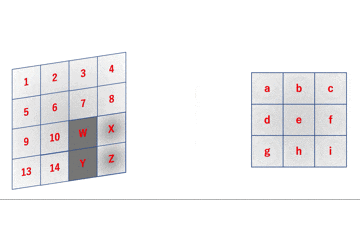
畳み込み層はこのフィルタが普通のレイヤでの重みに相当しています。あとはこのgifの通りに動作するコードを書けばいいわけですが、実はそのまま実装するととても実用に耐えない激重コードになってしまいます。
というのも、簡略化してこのgifの部分を実装すると
Image = I_h×I_wの配列
Filter = F_h×F_wの配列
Output = O_h×O_wの配列
for h in range(O_h):
h_lim = h + F_h
for w in range(O_w):
w_lim = w + F_w
Output[h, w] = Image[h:h_lim, w:w_lim] * Filter
のようになり、二重ループでnumpy配列にアクセスして入力の該当箇所に要素積を施していき、その結果を出力に保存していく、みたいなことをすることになります。
しかもこのループ、ここでは二重ループですが実際の入力は4次元ですので四重ループになってしまいます。すると簡単にループ回数が急増することは想像に難くないでしょう。
numpyにはfor文でアクセスすると遅くなるという仕様があるため、できるだけループでのアクセスは避けたいものです。そこで活躍するのがim2col関数です。
先のgifは
a = 1W + 2X + 5Y + 6Z \\
b = 2W + 3X + 6Y + 7Z \\
c = 3W + 4X + 7Y + 8Z \\
d = 5W + 6X + 9Y + 10Z \\
e = 6W + 7X + 10Y + 11Z \\
f = 7W + 8X + 11Y + 12Z \\
g = 9W + 10X + 13Y + 14Z \\
h = 10W + 11X + 14Y + 15Z \\
i = 11W + 12X + 15Y + 16Z
という感じとなっていますが、これを行列積で表すと
\left(
\begin{array}{c}
a \\
b \\
c \\
d \\
e \\
f \\
g \\
h \\
i
\end{array}
\right)^{\top}
=
\left(
\begin{array}{cccc}
W & X & Y & Z
\end{array}
\right)
\left(
\begin{array}{ccccccccc}
1 & 2 & 3 & 5 & 6 & 7 & 9 & 10 & 11 \\
2 & 3 & 4 & 6 & 7 & 8 & 10 & 11 & 12 \\
5 & 6 & 7 & 9 & 10 & 11 & 13 & 14 & 15 \\
6 & 7 & 8 & 10 & 11 & 12 & 14 & 15 & 16
\end{array}
\right)
となります。im2col関数は入力画像やフィルタをこんな感じの行列に変換するための関数になります。詳しくはこちらで解説しています。
さて、このim2col関数を用いることで前述の問題はだいぶ解消されます。が、もちろんim2col関数を用いると元の入力などの形状とは異なるためこのままでは誤差逆伝播法での学習が進められません。ということで逆の動作を行うcol2im関数を逆伝播時に噛ませる必要があります。詳しくはこちらで解説しています。
ここまでで簡単に畳み込み層の概要を説明しましたので、その設計図を示しておきます。
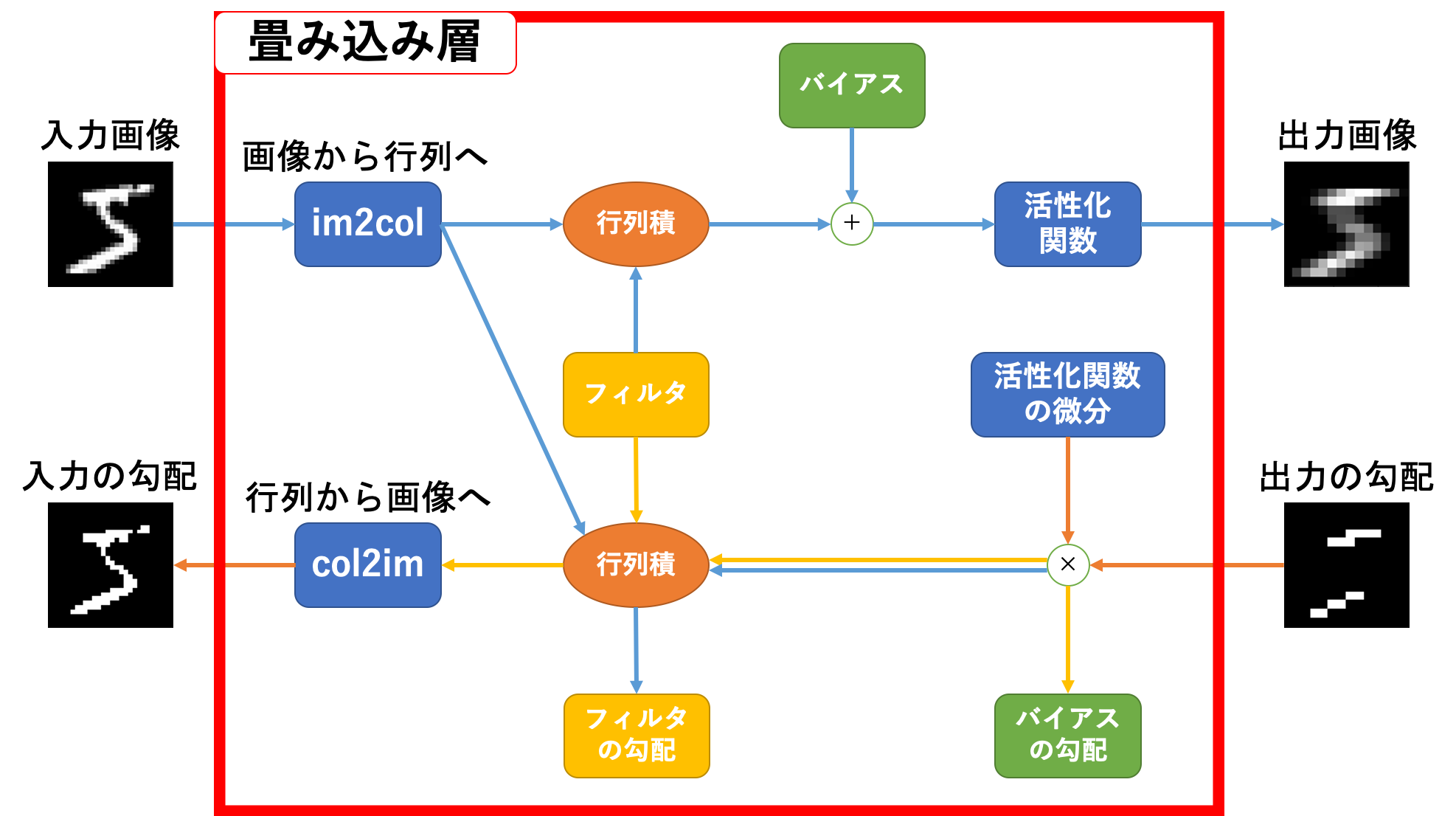
畳み込み層順伝播
順伝播から見ていきましょう。関係のある部分は下図のカラー部分です。
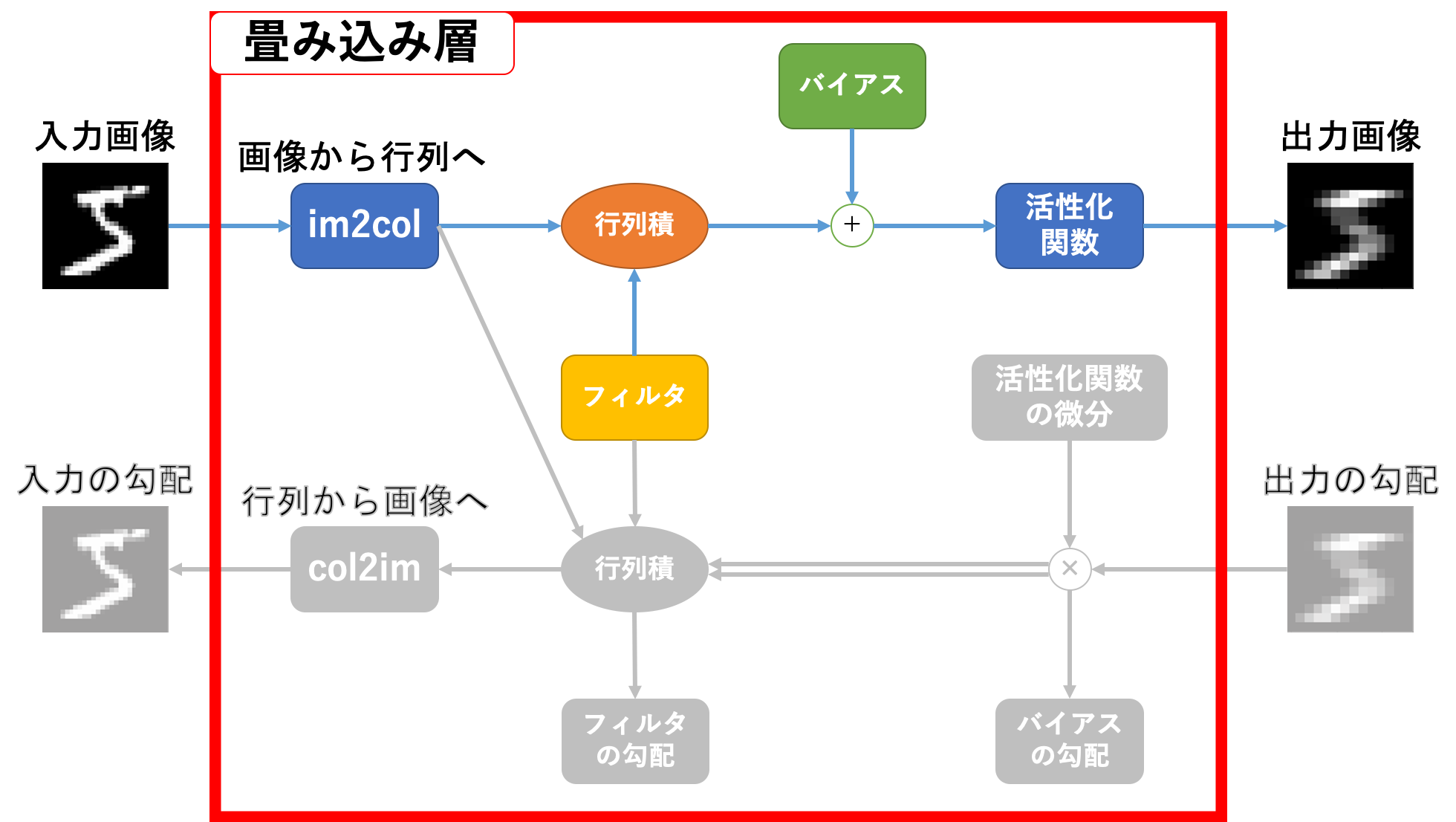
動作的には
- 入力画像を
im2col関数に投げる - 返り値とフィルタ(を変形したもの)とを行列積計算する。
- 2.の出力とバイアスとを足し算
- 活性化関数を通す
基本動作は通常のニューラルネットワークの順伝播と同じです。違うのはその前にim2col関数を挟むことくらいですね。
詳しく見ていきましょう。
まず畳み込み演算は以下の図のようになります。
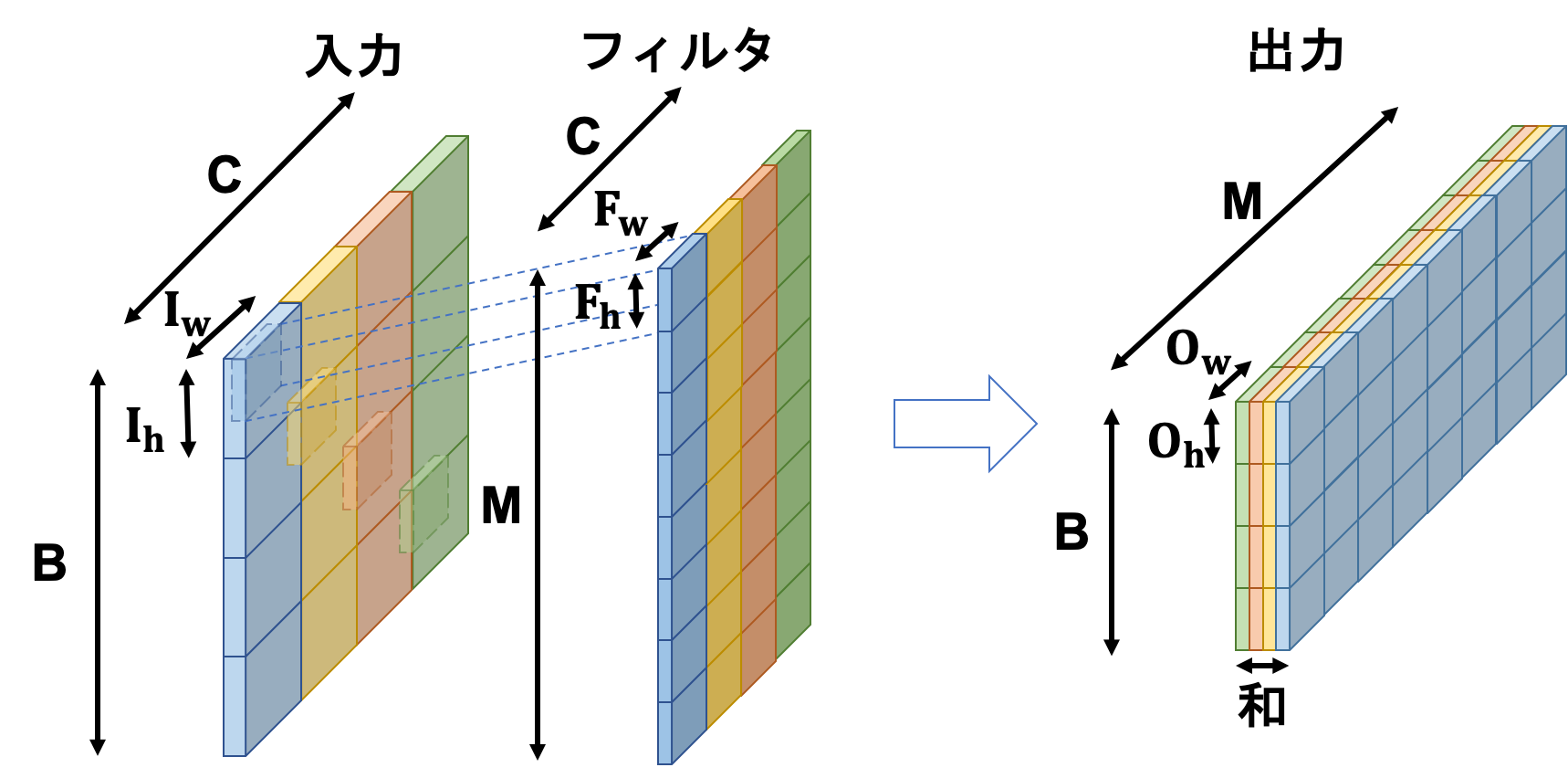
バイアスは省いています。
入力はバッチサイズ$B$、チャンネル数$C$、画像サイズ$(I_h, I_w)$のテンソルです。
フィルタは各チャンネルごとに$M$枚存在しており、入力と同じチャンネル数を持ち、フィルタサイズ$(F_h, F_w)$のテンソルです。
入力の各チャンネルに対応するチャンネルのフィルタを全てのバッチデータに対してフィルタリングを行い、結果として$(B, M, O_h, O_w)$という形状を持つテンソルができます。この処理を具体的にどう行うかを見ていきます。
入力及びフィルタを以下の図の通りに処理します。
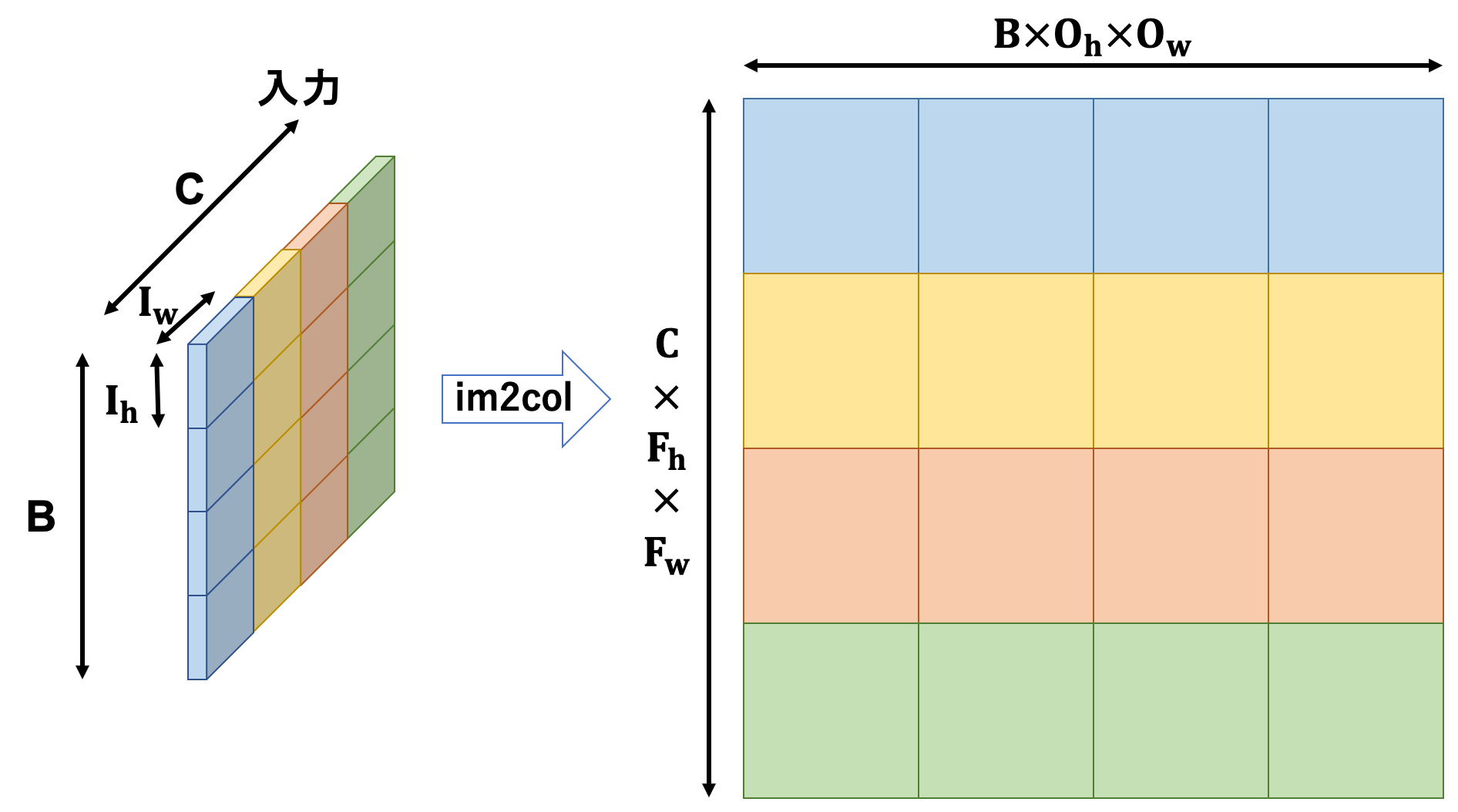
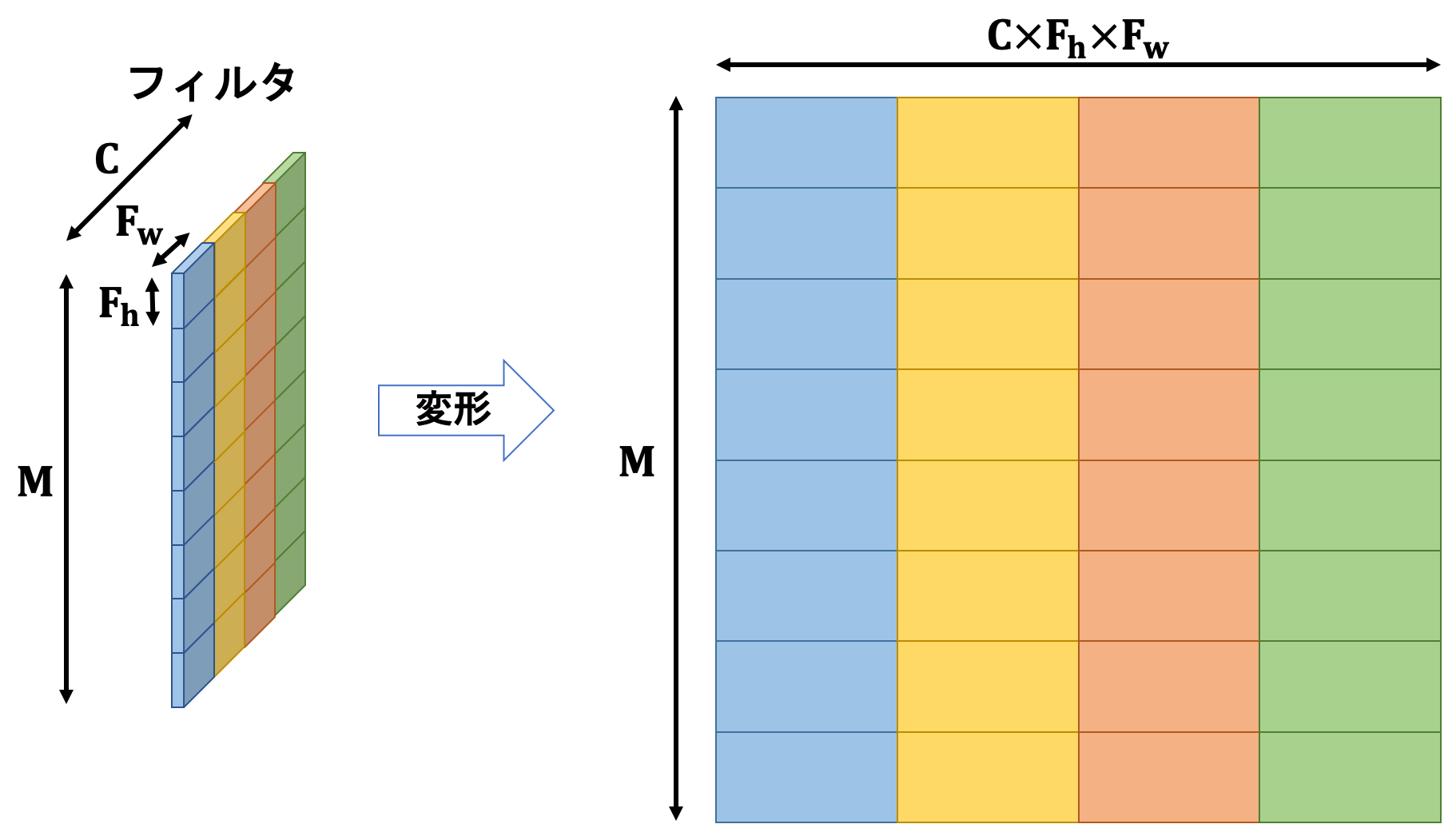
これにより4次元テンソルを2次元に落とし込むことができたため、行列積を行うことができるようになります。
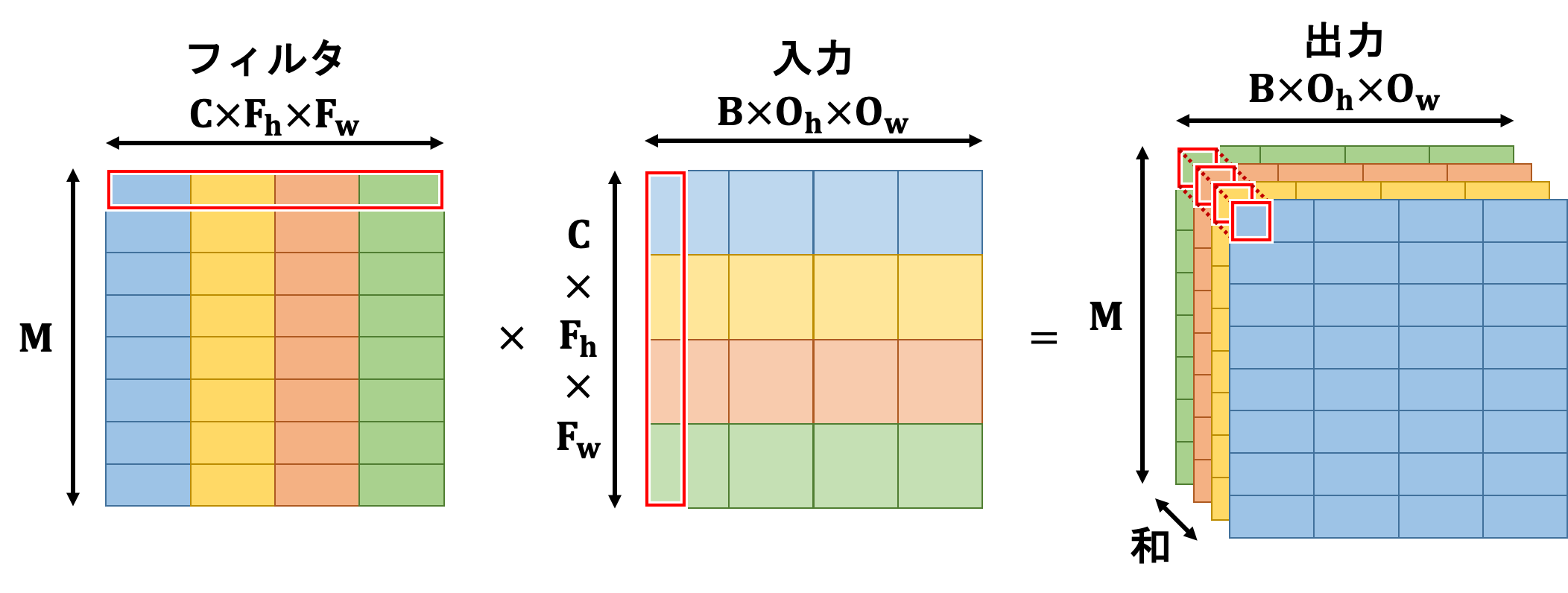
この出力にバイアス(形状は$(M, 1)$の2次元行列)を加えます。この時、numpyのブロードキャスト機能を用いて全ての列に同じ値を加算します。
その後この出力を変形、次元入れ替えすることで求める出力テンソルにします。
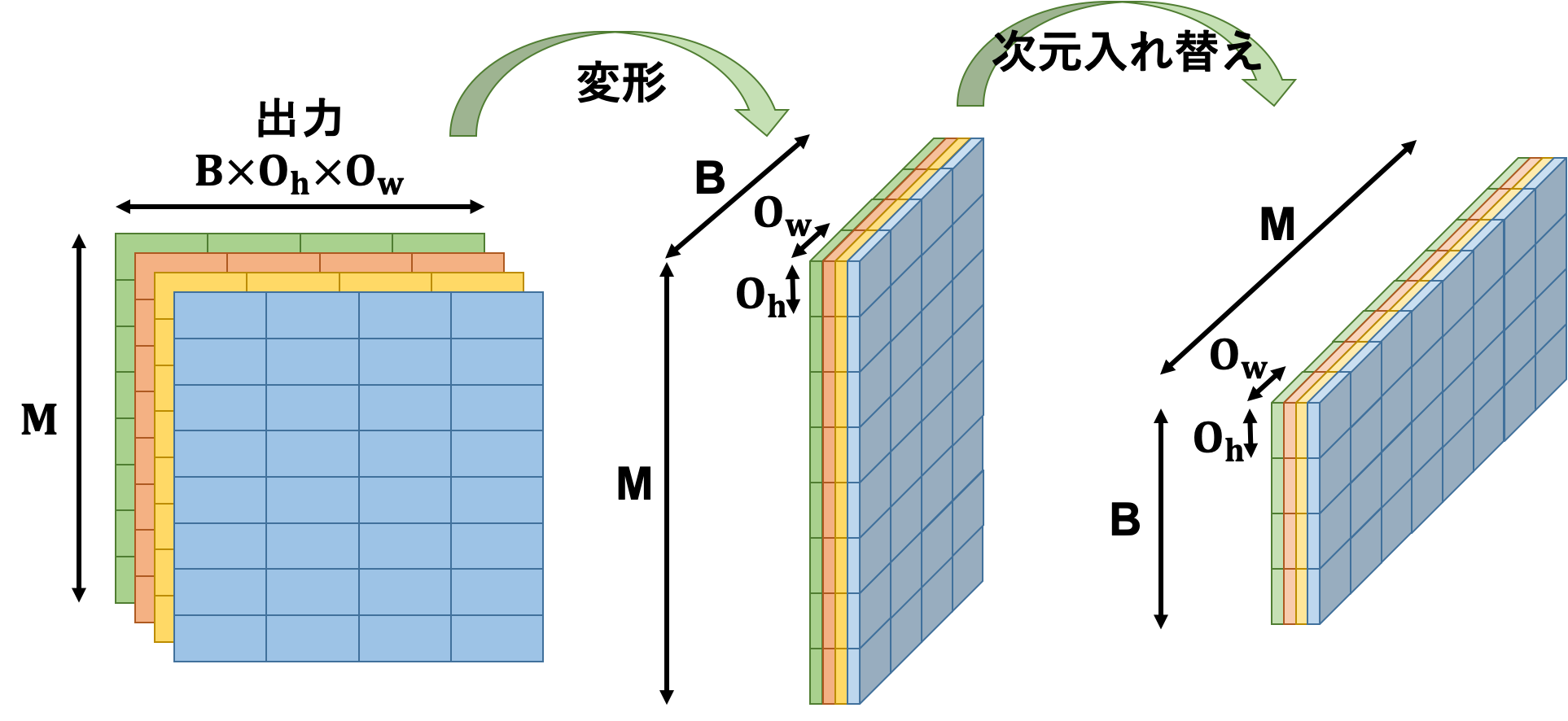
この出力テンソルを活性化関数に投げれば畳み込み層の順伝播の完了です。
畳み込み層逆伝播
続いて逆伝播です。関係している部分は下図のカラー部分です。
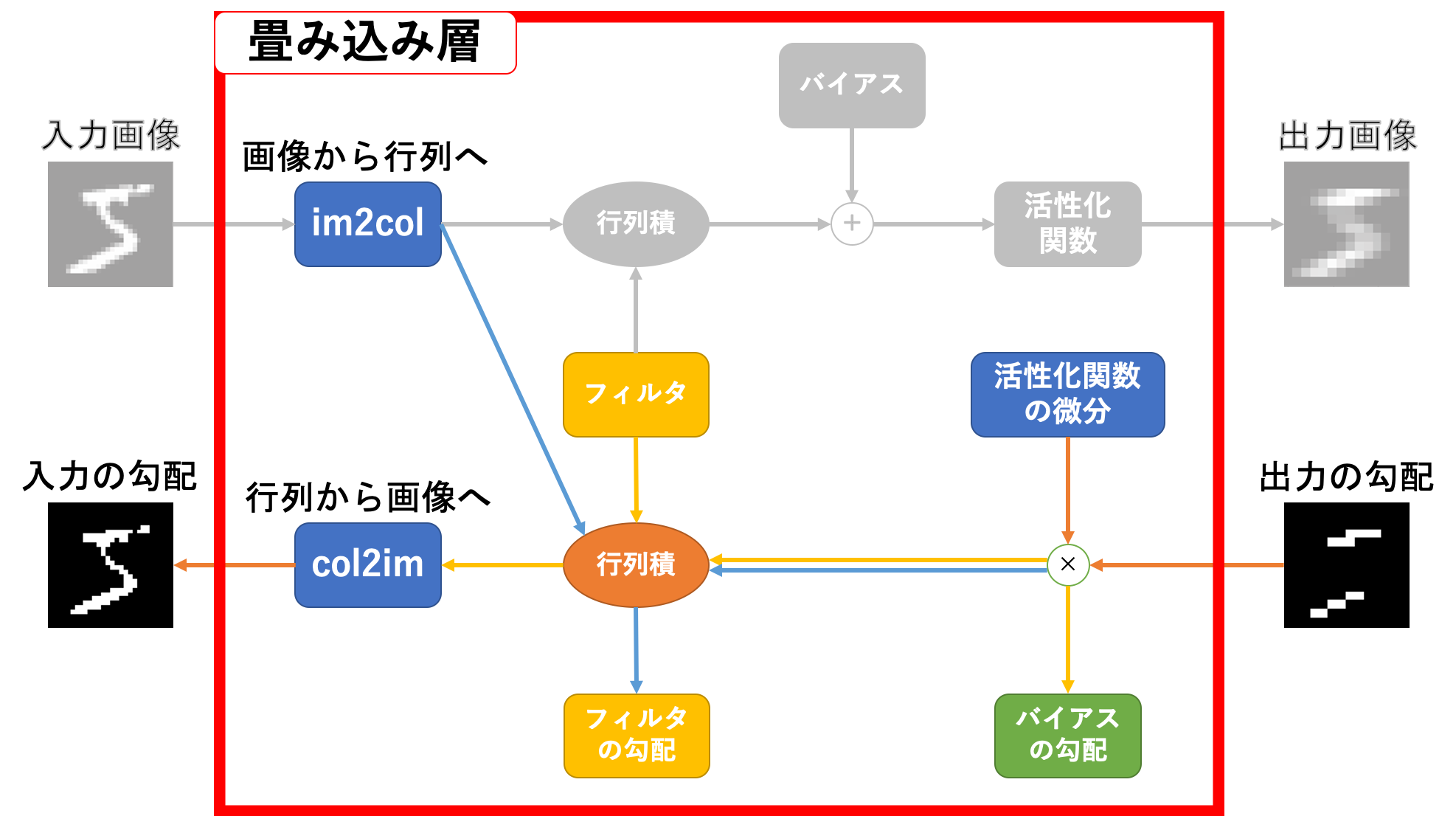
動作としては
- 出力の勾配と活性化関数の微分の要素積をとる
- 一つはバイアスの勾配として利用する
-
im2col関数を通した入力画像との行列積をとったものはフィルタの勾配として利用する - フィルタとの行列積をとったものは
col2im関数を通して入力の勾配として利用する
という感じです。
詳しく見ていきましょう。
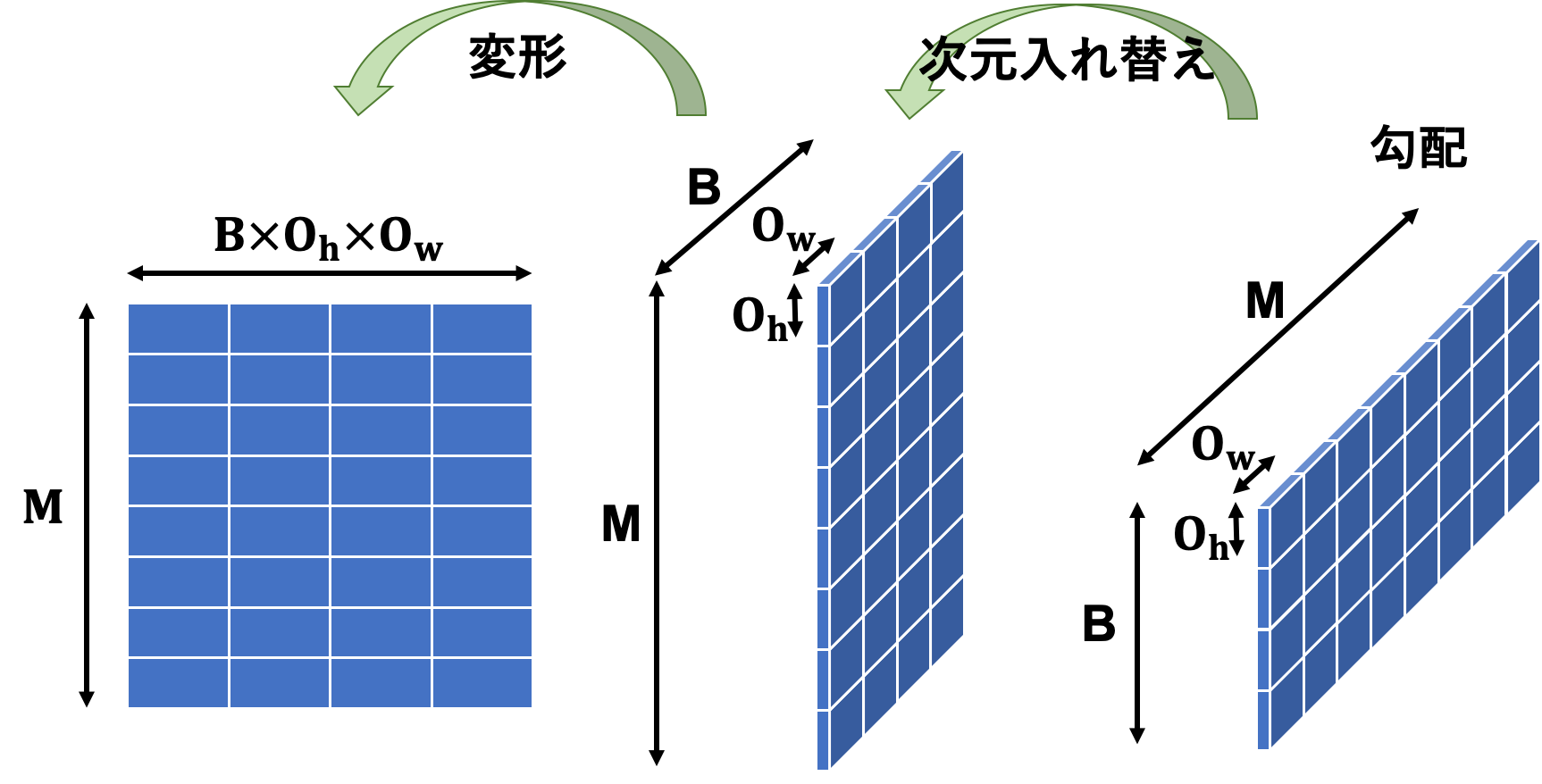
伝播してきた勾配は$(B, M, O_h, O_w)$のテンソルです。まずは順伝播の時とは逆順にこの勾配を変形します。
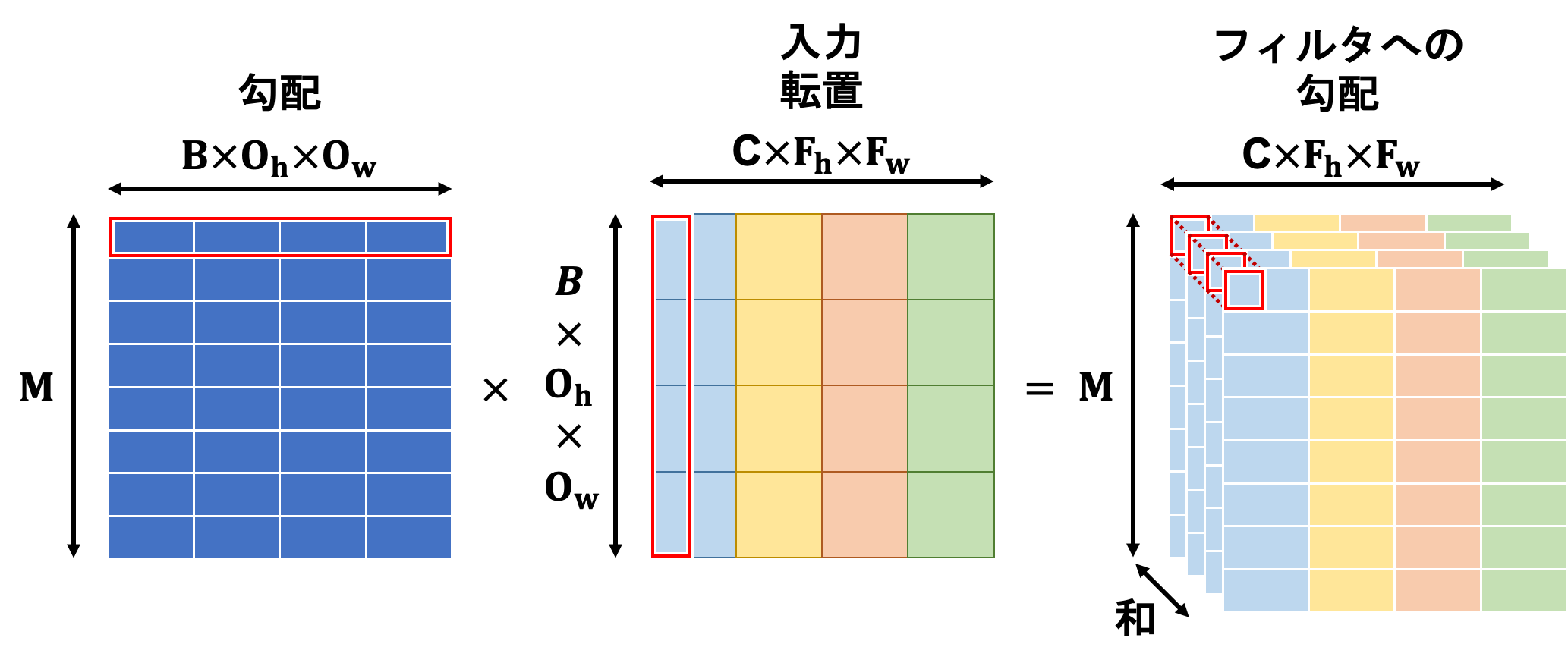
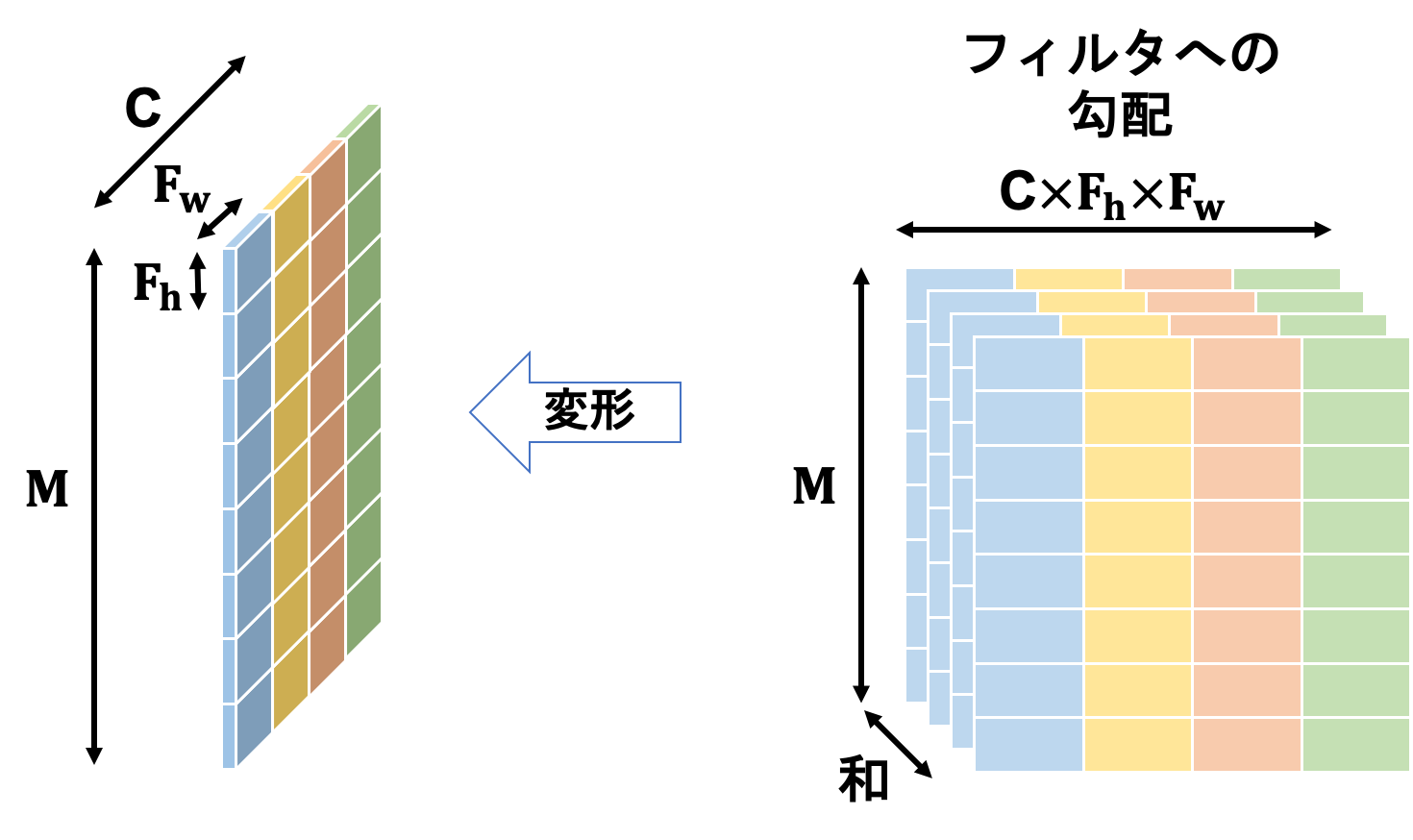
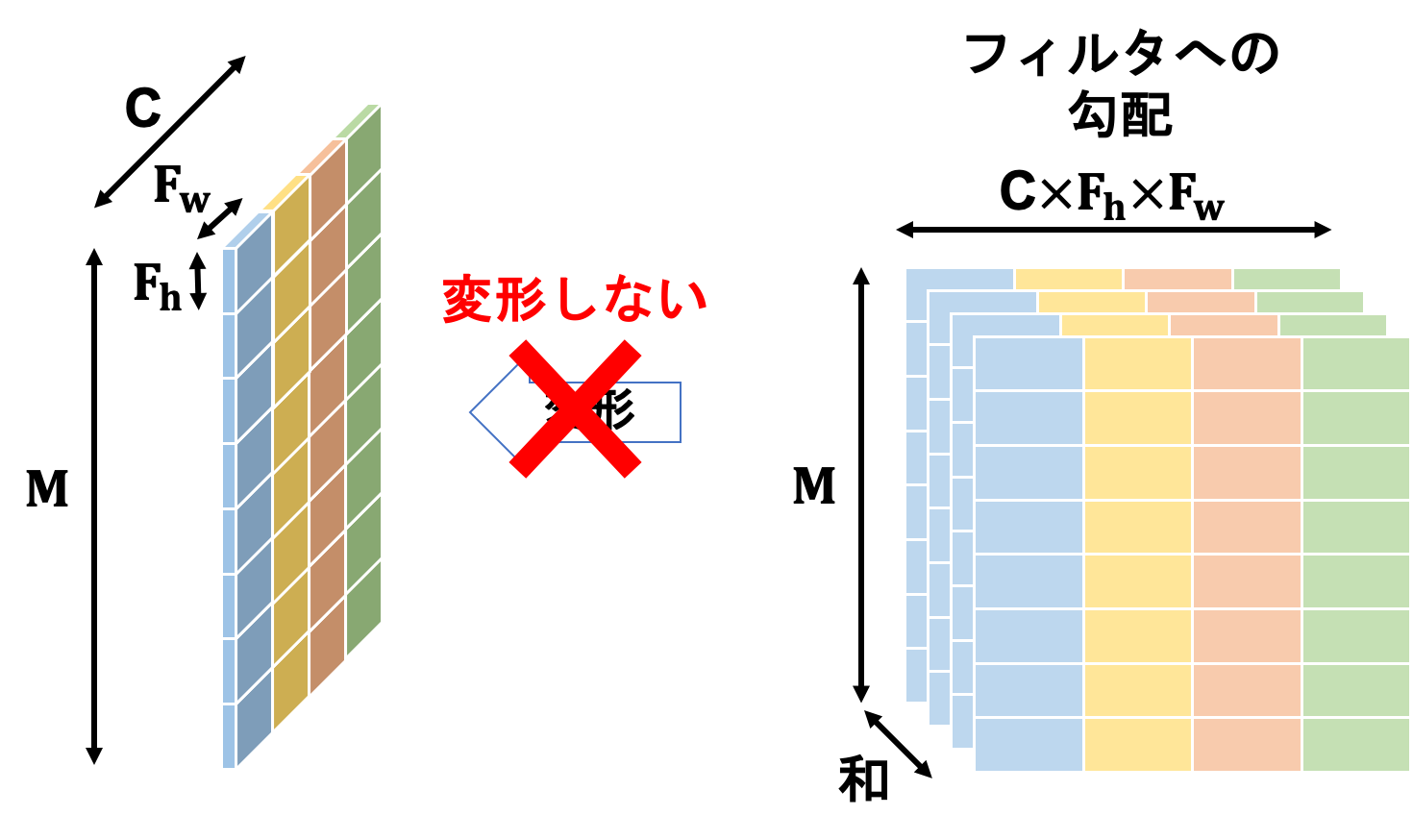
フィルタへの勾配は勾配と入力の行列積で計算されます。
得られた結果は2次元行列であるため、これを変形することでフィルタと同じ形状の4次元テンソルへ揃えます。
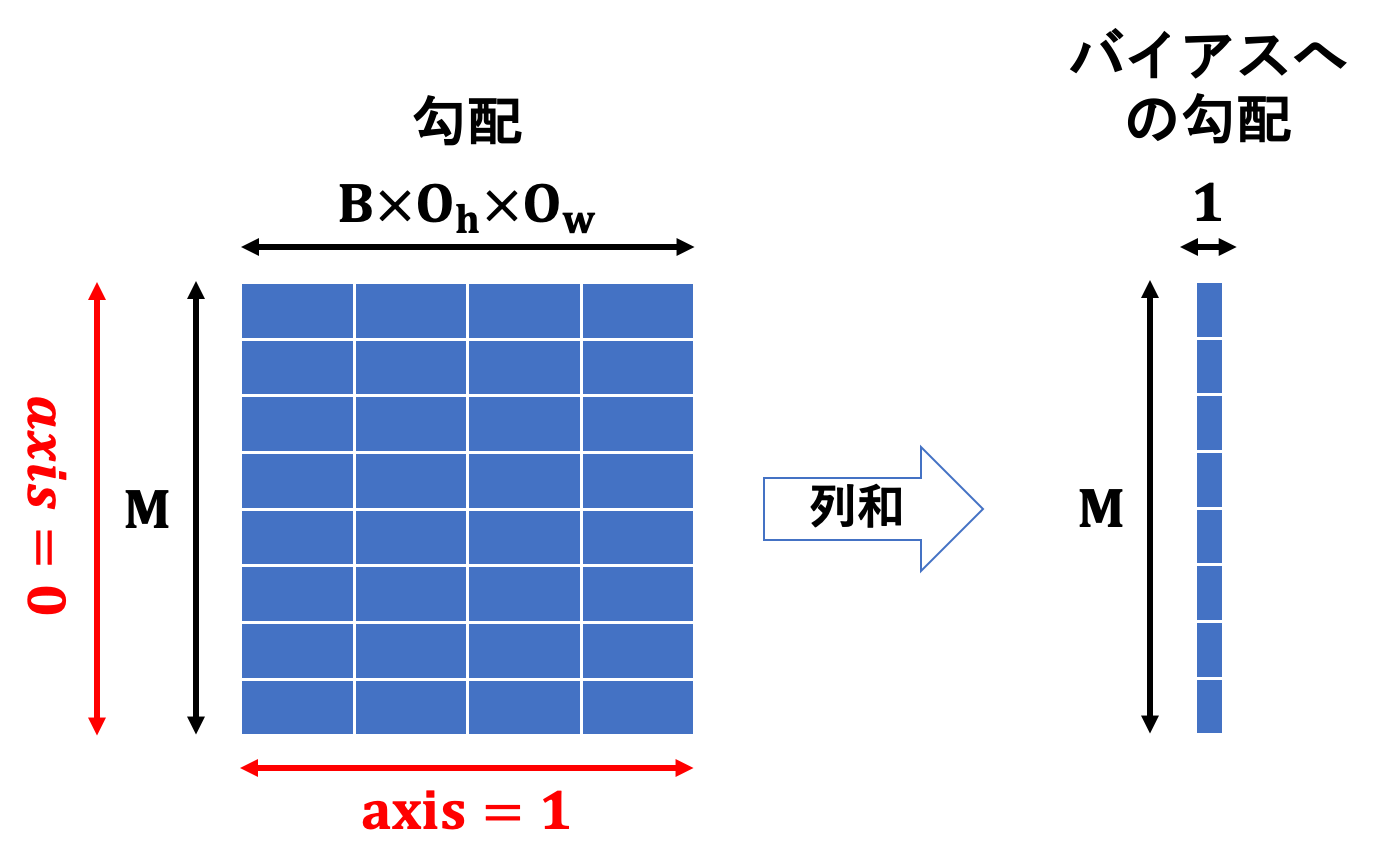
バイアスへの勾配について、順伝播の際に全ての列に同じ値を加算したことが鍵になります。同じ値をいくつかの要素に加算することが示すのは、以下の図のような形状のネットワークと同等である、ということです。
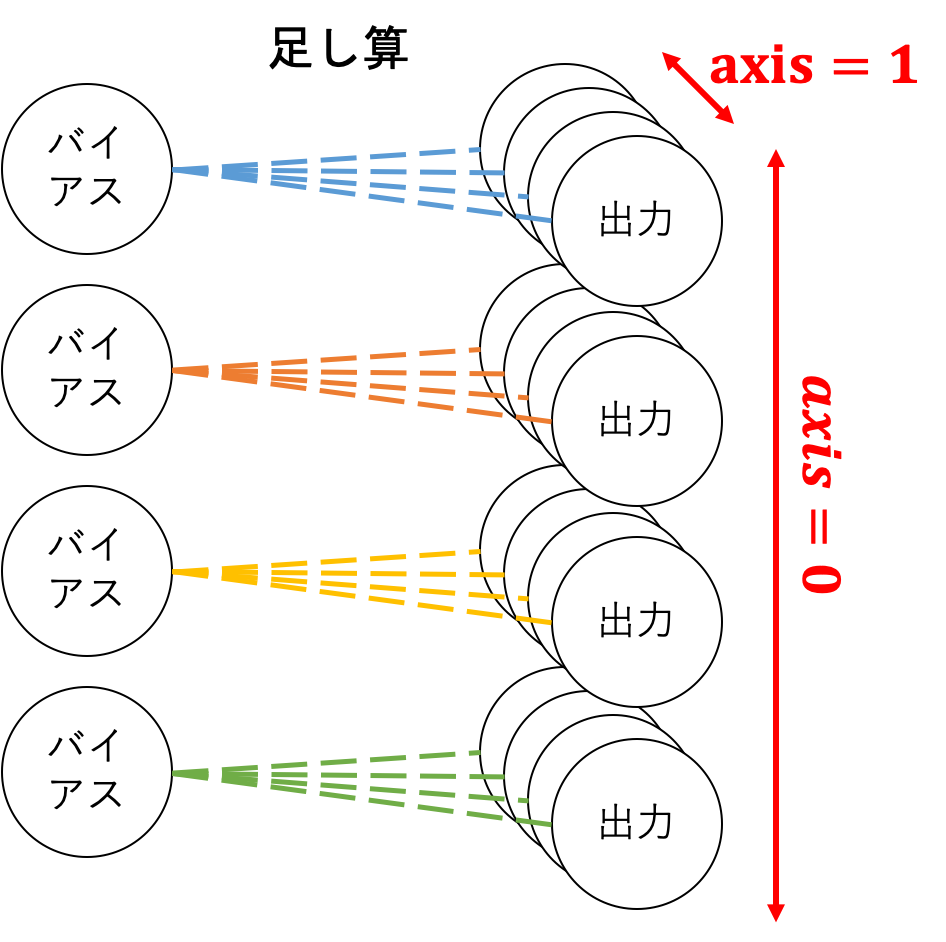
(数は適当です)
このため、$axis=1$つまり列方向からそれぞれ1つのバイアスに向けて逆伝播が行われるため、それらを足し合わせたものがバイアスへの勾配となります。
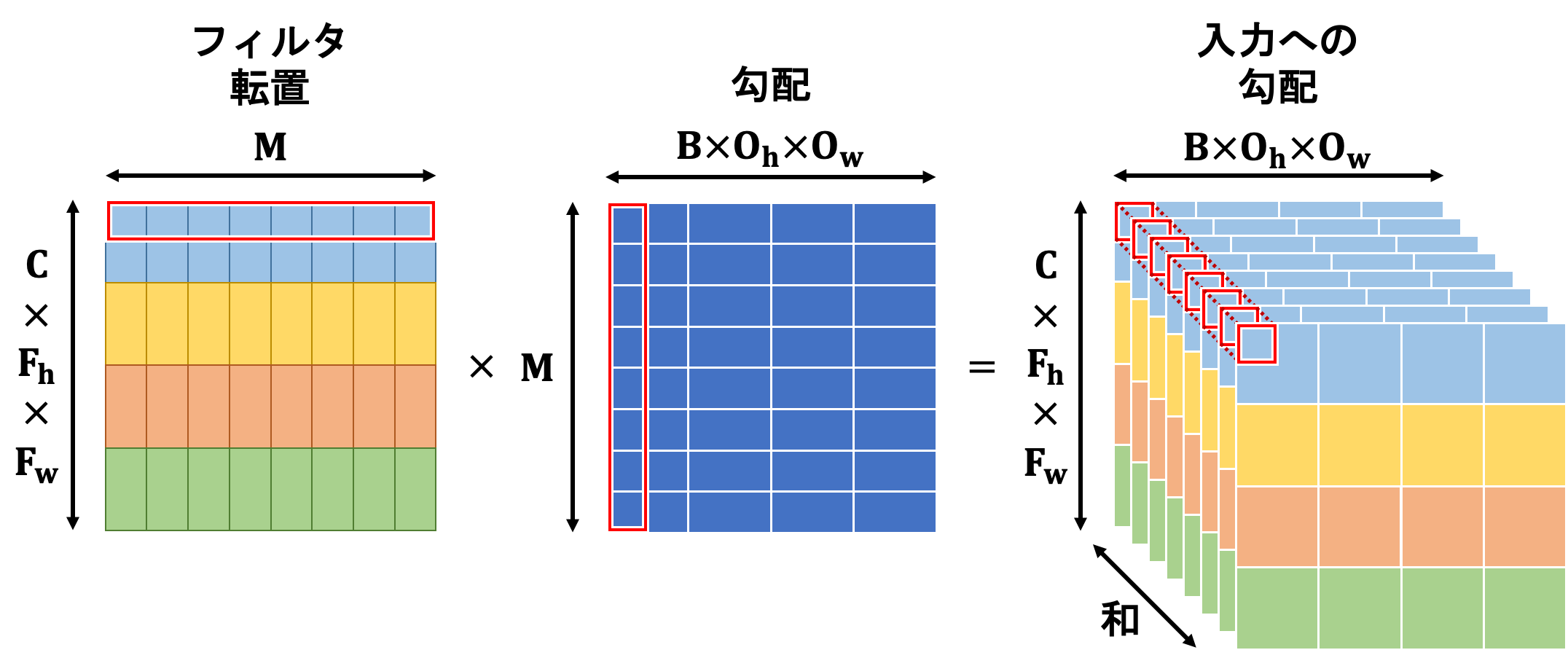
入力への勾配はフィルタと勾配の行列積で計算されます。
計算結果のテンソルを見てみるとわかるかと思いますが、形状が順伝播の時に入力テンソルをim2col関数に投げた結果と同じとなっています。そのため、逆の操作を行うcol2im関数にこれを投げることで入力への勾配テンソルが形成されます。
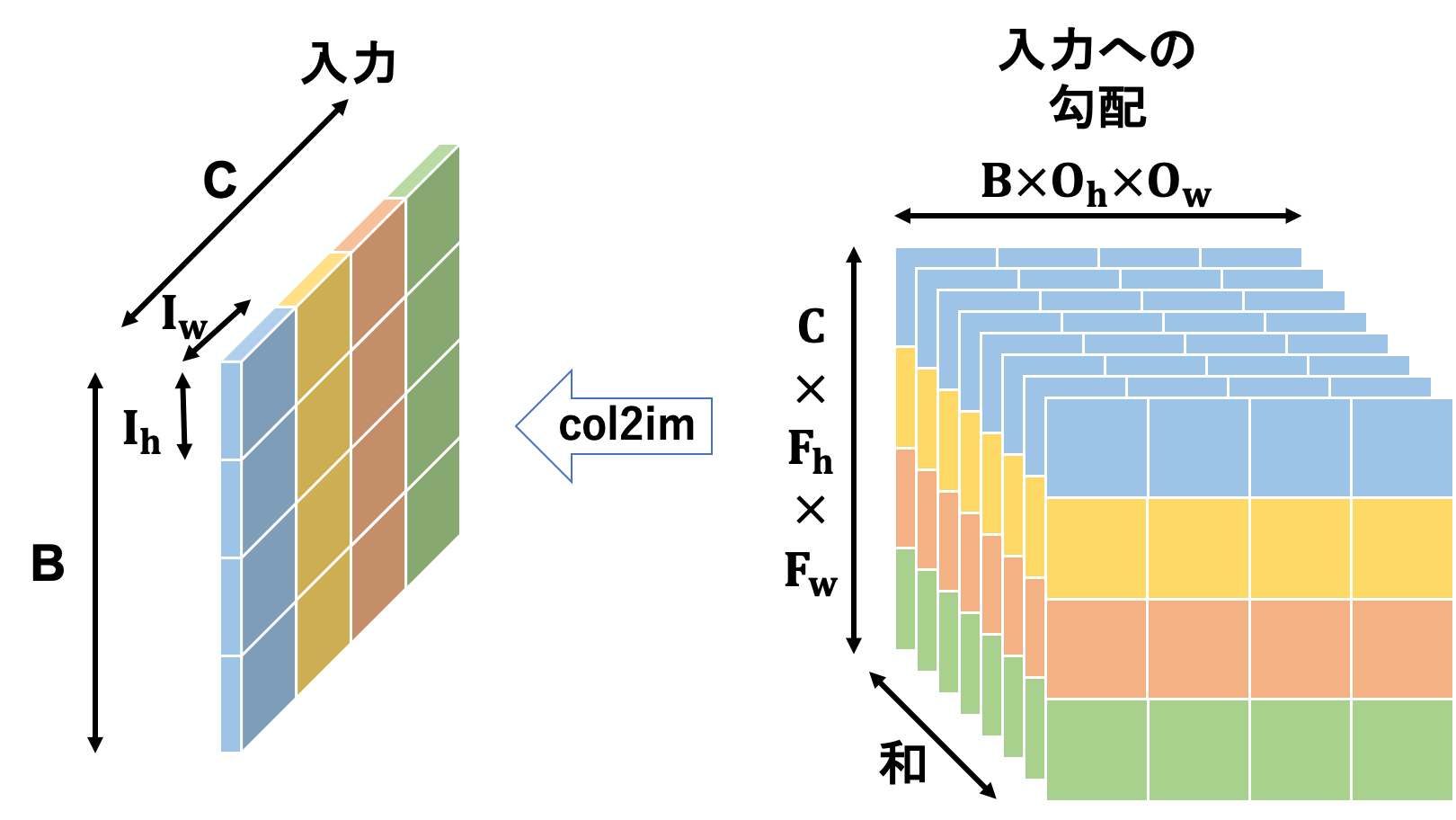
これで畳み込み層の逆伝播は完了です。
畳み込み層学習
さて、フィルタの変形は実は毎回行う必要がありません。最初に1回行うだけで良いです。その理由は「フィルタは毎回同じ変形をするのでわざわざ繰り返し行う必要がない」ためです。
フィルタは最初に変形したあとそのまま、ということは逆伝播で計算したフィルタへの勾配も変形する必要はありません。
そんなこんなで、畳み込み層の学習は通常のレイヤと同じ形になります。
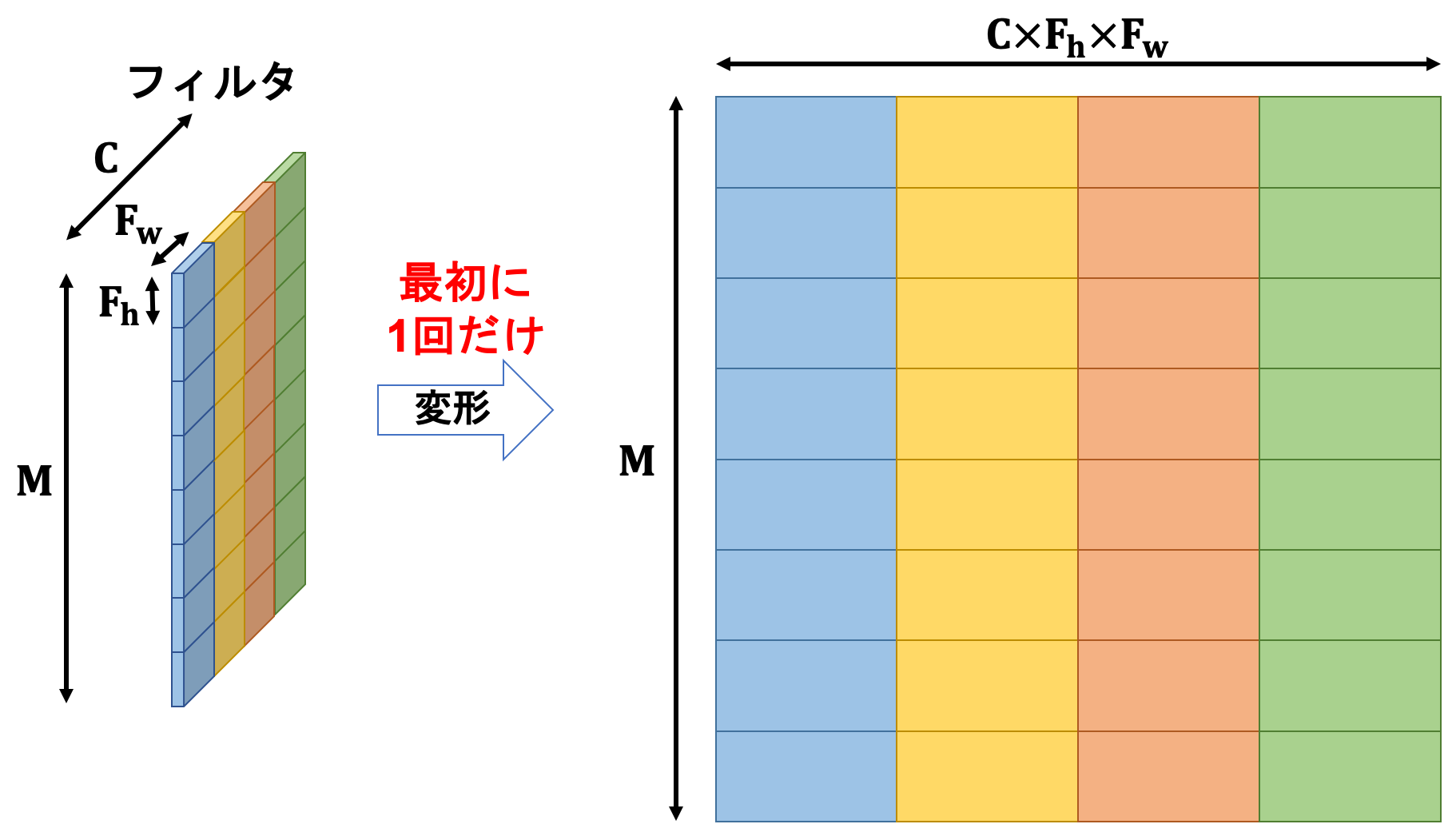
畳み込み層実装
ということで実装します。ただしBaseLayerを継承させるために少しの工夫が必要です。
conv.py
import numpy as np
class ConvLayer(BaseLayer):
def __init__(self, *, I_shape=None, F_shape=None,
stride=1, pad="same",
name="", wb_width=5e-2,
act="ReLU", opt="Adam",
act_dic={}, opt_dic={}, **kwds):
self.name = name
if I_shape is None:
raise KeyError("Input shape is None.")
if F_shape is None:
raise KeyError("Filter shape is None.")
if len(I_shape) == 2:
C, I_h, I_w = 1, *I_shape
else:
C, I_h, I_w = I_shape
self.I_shape = (C, I_h, I_w)
if len(F_shape) == 2:
M, F_h, F_w = 1, *F_shape
else:
M, F_h, F_w = F_shape
self.F_shape = (M, C, F_h, F_w)
if isinstance(stride, tuple):
stride_ud, stride_lr = stride
else:
stride_ud = stride
stride_lr = stride
self.stride = (stride_ud, stride_lr)
if isinstance(pad, tuple):
pad_ud, pad_lr = pad
elif isinstance(pad, int):
pad_ud = pad
pad_lr = pad
elif pad == "same":
pad_ud = 0.5*((I_h - 1)*stride_ud - I_h + F_h)
pad_lr = 0.5*((I_w - 1)*stride_lr - I_w + F_w)
self.pad = (pad_ud, pad_lr)
O_h = get_O_shape(I_h, F_h, stride_ud, pad_ud)
O_w = get_O_shape(I_w, F_w, stride_lr, pad_lr)
self.O_shape = (M, O_h, O_w)
self.n = np.prod(self.O_shape)
# フィルタとバイアスを設定
self.w = wb_width*np.random.randn(*self.F_shape).reshape(M, -1).T
self.b = wb_width*np.random.randn(M)
# 活性化関数(クラス)を取得
self.act = get_act(act, **act_dic)
# 最適化子(クラス)を取得
self.opt = get_opt(opt, **opt_dic)
def forward(self, x):
B = x.shape[0]
M, O_h, O_w = self.O_shape
x, _, self.pad_state = im2col(x, self.F_shape,
stride=self.stride,
pad=self.pad)
super().forward(x.T)
return self.y.reshape(B, O_h, O_w, M).transpose(0, 3, 1, 2)
def backward(self, grad):
B = grad.shape[0]
I_shape = B, *self.I_shape
M, O_h, O_w = self.O_shape
grad = grad.transpose(0, 2, 3, 1).reshape(-1, M)
super().backward(grad)
self.grad_x = col2im(self.grad_x.T, I_shape, self.O_shape,
stride=self.stride, pad=self.pad_state)
return self.grad_x
どのあたりを工夫しているのか説明していきます。
工夫せずに、先ほどまでで説明した通りに実装すると以下のようになります。
工夫なしver.
import numpy as np
class ConvLayer(BaseLayer):
def __init__(self, *, I_shape=None, F_shape=None,
stride=1, pad="same",
name="", wb_width=5e-2,
act="ReLU", opt="Adam",
act_dic={}, opt_dic={}, **kwds):
self.name = name
if I_shape is None:
raise KeyError("Input shape is None.")
if F_shape is None:
raise KeyError("Filter shape is None.")
if len(I_shape) == 2:
C, I_h, I_w = 1, *I_shape
else:
C, I_h, I_w = I_shape
self.I_shape = (C, I_h, I_w)
if len(F_shape) == 2:
M, F_h, F_w = 1, *F_shape
else:
M, F_h, F_w = F_shape
self.F_shape = (M, C, F_h, F_w)
_, O_shape, self.pad_state = im2col(np.zeros((1, *self.I_shape)), self.F_shape,
stride=stride, pad=pad)
self.O_shape = (M, *O_shape)
self.stride = stride
self.n = np.prod(self.O_shape)
# フィルタとバイアスを設定
self.w = wb_width*np.random.randn(*self.F_shape).reshape(M, -1)
self.b = wb_width*np.random.randn(M, 1)
# 活性化関数(クラス)を取得
self.act = get_act(act, **act_dic)
# 最適化子(クラス)を取得
self.opt = get_opt(opt, **opt_dic)
def forward(self, x):
B = x.shape[0]
M, O_h, O_w = self.O_shape
self.x, _, self.pad_state = im2col(x, self.F_shape,
stride=self.stride,
pad=self.pad)
self.u = self.w@self.x + self.b
self.u = self.u.reshape(M, B, O_h, O_w).transpose(1, 0, 2, 3)
self.y = self.act.forward(self.u)
return self.y
def backward(self, grad):
B = grad.shape[0]
I_shape = B, *self.I_shape
_, O_h, O_w = self.O_shape
dact = grad*self.act.backward(self.u, self.y)
dact = dact.transpose(1, 0, 2, 3).reshape(M, -1)
self.grad_w = dact@self.x.T
self.grad_b = np.sum(dact, axis=1).reshape(M, 1)
self.grad_x = self.w.T@dact
self.grad_x = col2im(self.grad_x, I_shape, self.O_shape,
stride=self.stride, pad=self.pad_state)
return self.grad_x
BaseLayerとの差異を、コードを省略しながら細かく見ていきます。
| 注目部分 | BaseLayer |
形状 | ConvLayer |
形状 | |
|---|---|---|---|---|---|
| w | randn(prev, n) | $(prev, n)$ | randn(*F_shape).reshape(M, -1) | $(M, CF_hF_w)$ | |
| b | randn(n) | $(n, )$ | randn(M, 1) | $(M, 1)$ | |
| x | - | $(B, prev)$ | im2col(x) | $(CF_hF_w, BO_hO_w)$ | |
| u | x@w + b | $(B, prev)@(prev, n)+(n)=(B, n)$ | w@x + b | $(M, CF_hF_w)@(CF_hF_w, BO_hO_w)+(M, 1)=(M, BO_hO_w)$ | |
| u | - | - | u.reshape(M, B, O_h, O_w).transpose(1, 0, 2, 3) | $(B, M, O_h, O_w)$ | |
| y | act.forward(u) | $(B, n)$ | act.forward(u) | $(B, M, O_h, O_w)$ | |
| grad | - | $(B, n)$ | - | $(B, M, O_h, O_w)$ | |
| dact | grad*act.backward(u, y) | $(B, n)$ | grad*act.backward(u, y) | $(B, M, O_h, O_w)$ | |
| dact | - | - | dact.transpose(1, 0, 2, 3).reshape(M, -1) | $(M, BO_hO_w)$ | |
| grad_w | x.T@dact | $(prev, B)@(B, n)=(prev, n)$ | dact@x.T | $(M, BO_hO_w)@(BO_hO_w, CF_hF_w)=(M, CF_hF_w)$ | |
| grad_b | sum(dact, axis=0) | $(n)$ | sum(dact, axis=1).reshape(M, 1) | $(M, 1)$ | |
| grad_x | dact@w.T | $(B, n)@(n, prev)=(B, prev)$ | w.T@dact | $(CF_hF_w, M)@(M, BO_hO_w)=(CF_hF_w, BO_hO_w)$ | |
| grad_x | - | - | col2im(grad_x) | $(B, C, I_h, I_w)$ |
まずは順伝播を揃えましょう。
順伝播の最も異なる点はuの計算ですね。
\boldsymbol{x}@\boldsymbol{w} + \boldsymbol{b} \quad \Leftrightarrow \quad \boldsymbol{w}@\boldsymbol{x} + \boldsymbol{b}
行列積は$\boldsymbol{w}@\boldsymbol{x} = \boldsymbol{x}^{\top}@\boldsymbol{w}^{\top}$とすることで順番を逆にすることができるため、
\begin{align}
\boldsymbol{x} &\leftarrow \textrm{im2col}(\boldsymbol{x})^{\top} = (BO_hO_w, CF_hF_w) \\
\boldsymbol{w} &\leftarrow \boldsymbol{w}^{\top} = (CF_hF_w, M) \\
\boldsymbol{b} & \leftarrow (M, )
\end{align}
のようにしておくことで順伝播の数式と揃えることが可能です。また、バイアスについてもnumpyのブロードキャスト機能を有効にするために$(M, 1)$とわざわざ2次元行列としていたのを1次元配列にすることができます。
このように順伝播を変更すると
\boldsymbol{x}@\boldsymbol{w} + \boldsymbol{b} = (BO_hO_w, CF_hF_w)@(CF_hF_w, M) + (M) = (BO_hO_w, M)
と計算されるので、BaseLayerのforwardで計算したあと、次の層への伝播をself.y.reshape(B, O_h, O_w, M).transpose(0, 3, 1, 2)とすることで$(B, M, O_h, O_w)$と変形することができます。
また、工夫した方のコードを見るとreturn文で上述の変形をして流していますが、これによりuとyの形状が$(BO_hO_w, M)$のままとなります。これはこのままで大丈夫です。
続いて逆伝播です。勾配gradは$(B, M, O_h, O_w)$となっており、このままではgrad*act.backward(u, y)の要素積計算ができません。
\boldsymbol{grad} \otimes \textrm{act.backward}(\boldsymbol{u}, \boldsymbol{y}) = (B, M, O_h, O_w) \otimes (BO_hO_w, M)
ということでgradを変形して揃えましょう.
grad.transpose(0, 2, 3, 1).reshape(-1, M)とすればOKですね。
この後はBaseLayerのbackwardに投げれば
\begin{array}[cccc]
d\boldsymbol{dact} &= \boldsymbol{grad} \otimes \textrm{act.backward}(\boldsymbol{u}, \boldsymbol{y}) &= (BO_hO_w, M) & \\
\boldsymbol{grad_w} &= \boldsymbol{x}^{\top}@\boldsymbol{dact} &= (CF_hF_w, BO_hO_w)@(BO_hO_w, M) &= (CF_hF_w, M)\\
\boldsymbol{grad_b} &= \textrm{sum}(\boldsymbol{dact}, \textrm{axis}=0) &= (M, ) & \\
\boldsymbol{grad_x} &= \boldsymbol{dact}@\boldsymbol{w}^{\top} &= (BO_hO_w, M)@(M, CF_hF_w) &= (BO_hO_w, CF_hF_w)
\end{array}
となるので
\boldsymbol{grad_x} \leftarrow \textrm{col2im}(\boldsymbol{grad_x}^{\top}) = (B, C, I_h, I_w)
とすればOKです。
BaseLayerのupdate関数については前述の通り変更する必要がありません。
よって、これで畳み込み層の完成です。
プーリング層
続いてプーリング層です。まずプーリング層とは、入力画像の中から重要だと思われる情報のみを抜き出してデータサイズを小さくするレイヤです。この場合の重要な情報というのは、大抵の場合は最大値だったり平均値だったりします。
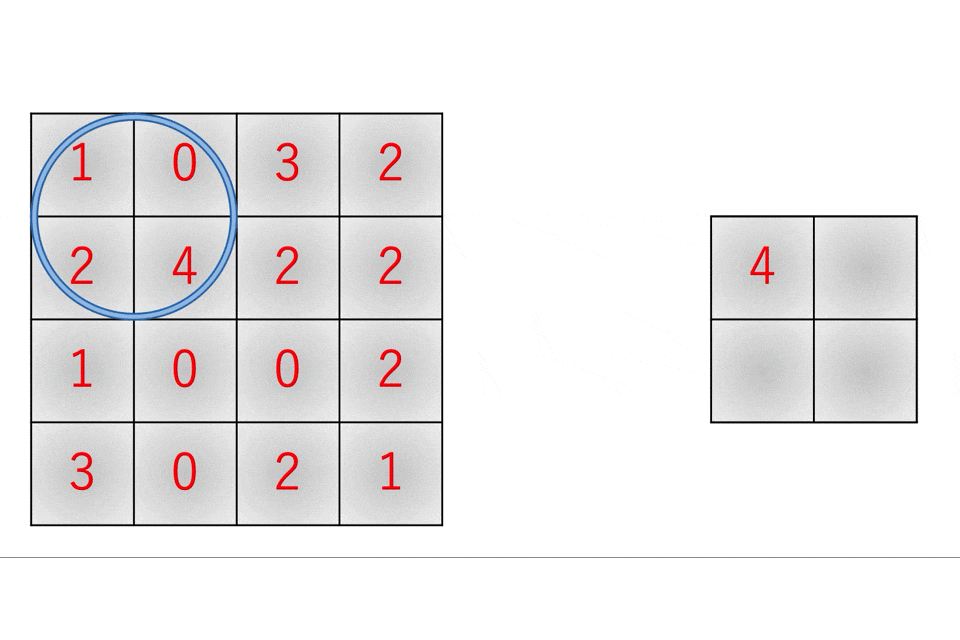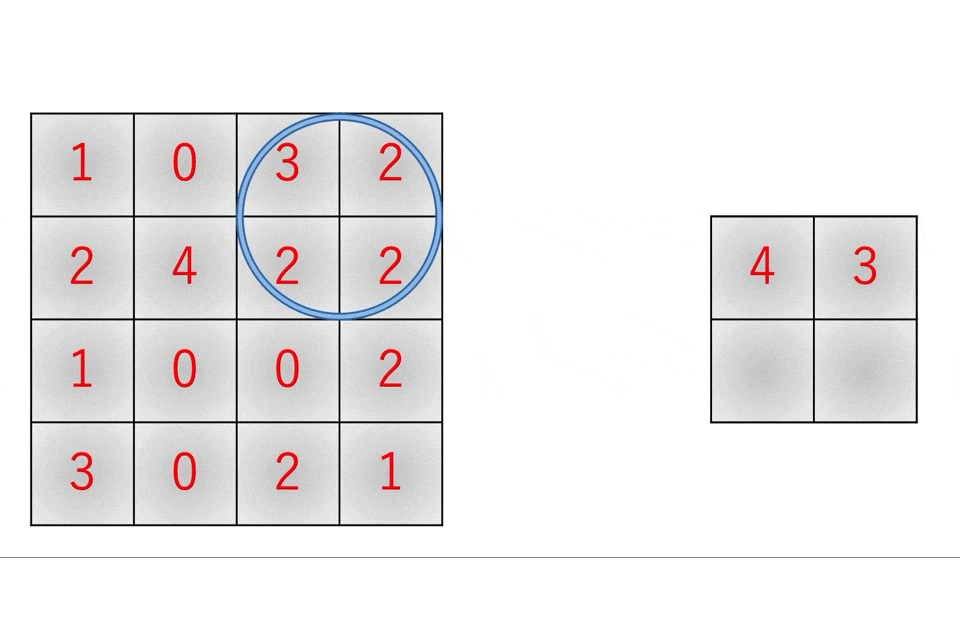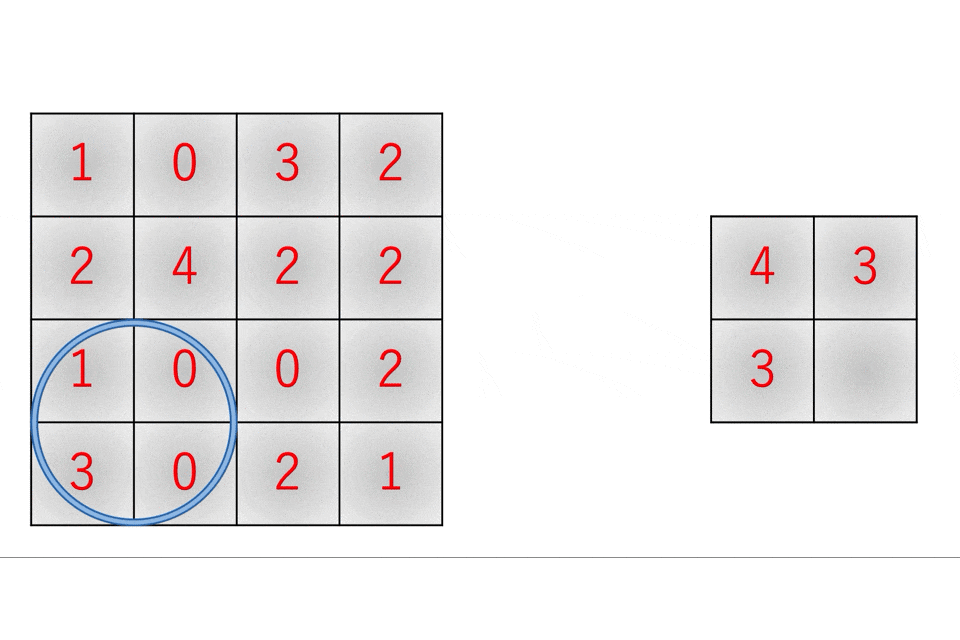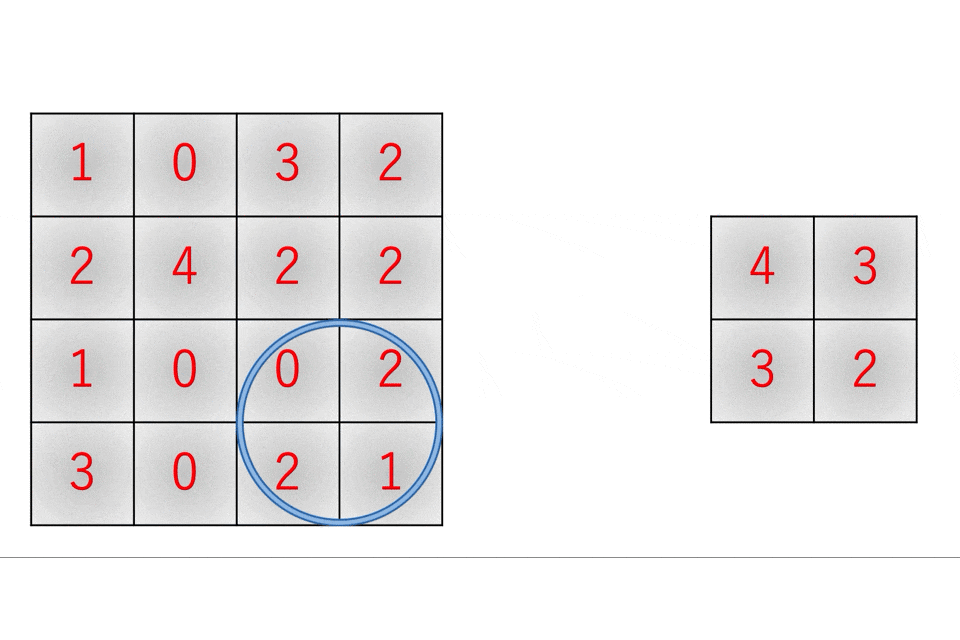
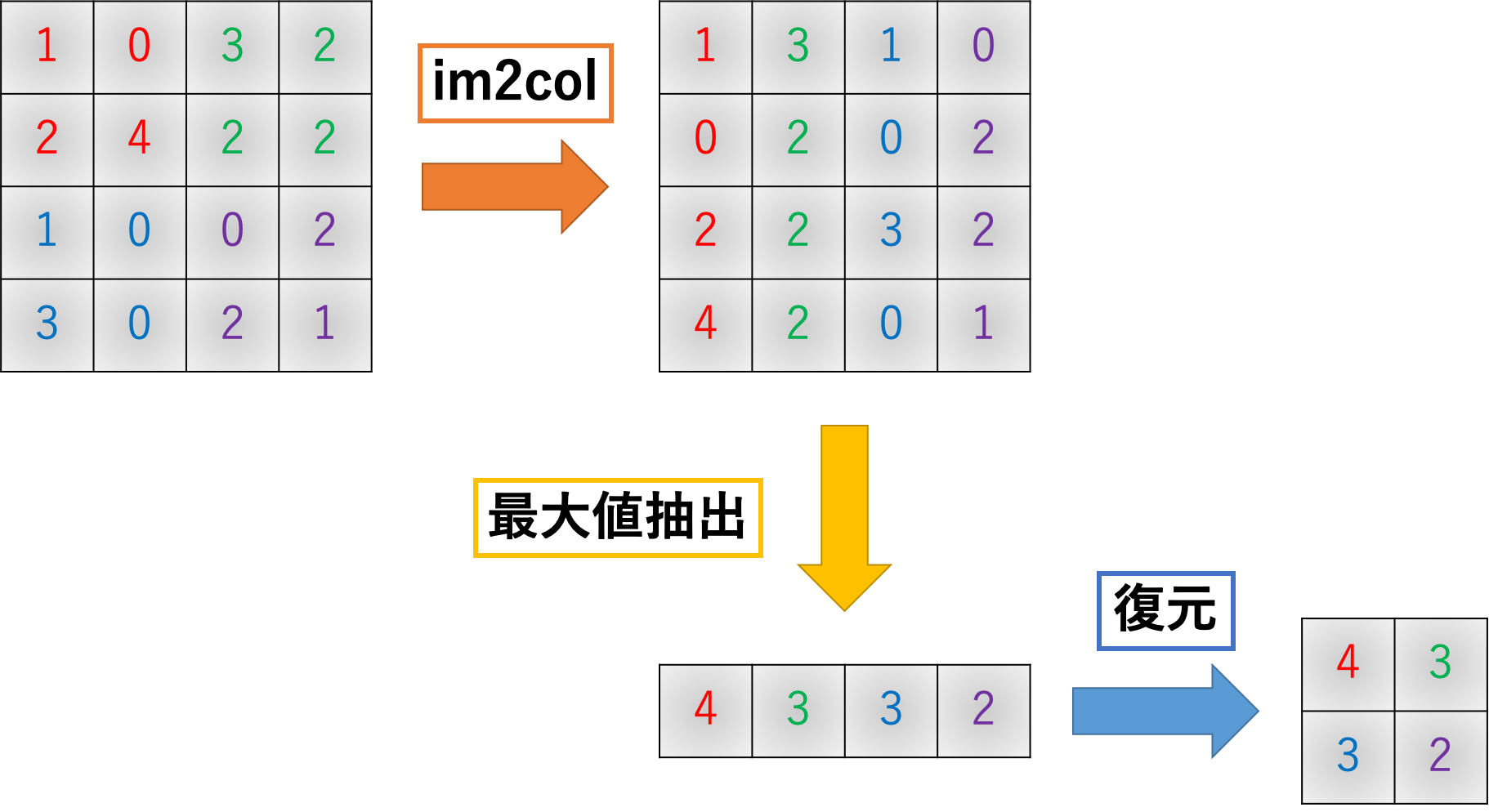
また、これを実装する際には畳み込み層と同様にim2col関数やcol2im関数を利用することで高速かつ効率的になります。
プーリング層の設計図は次のような感じとなります。
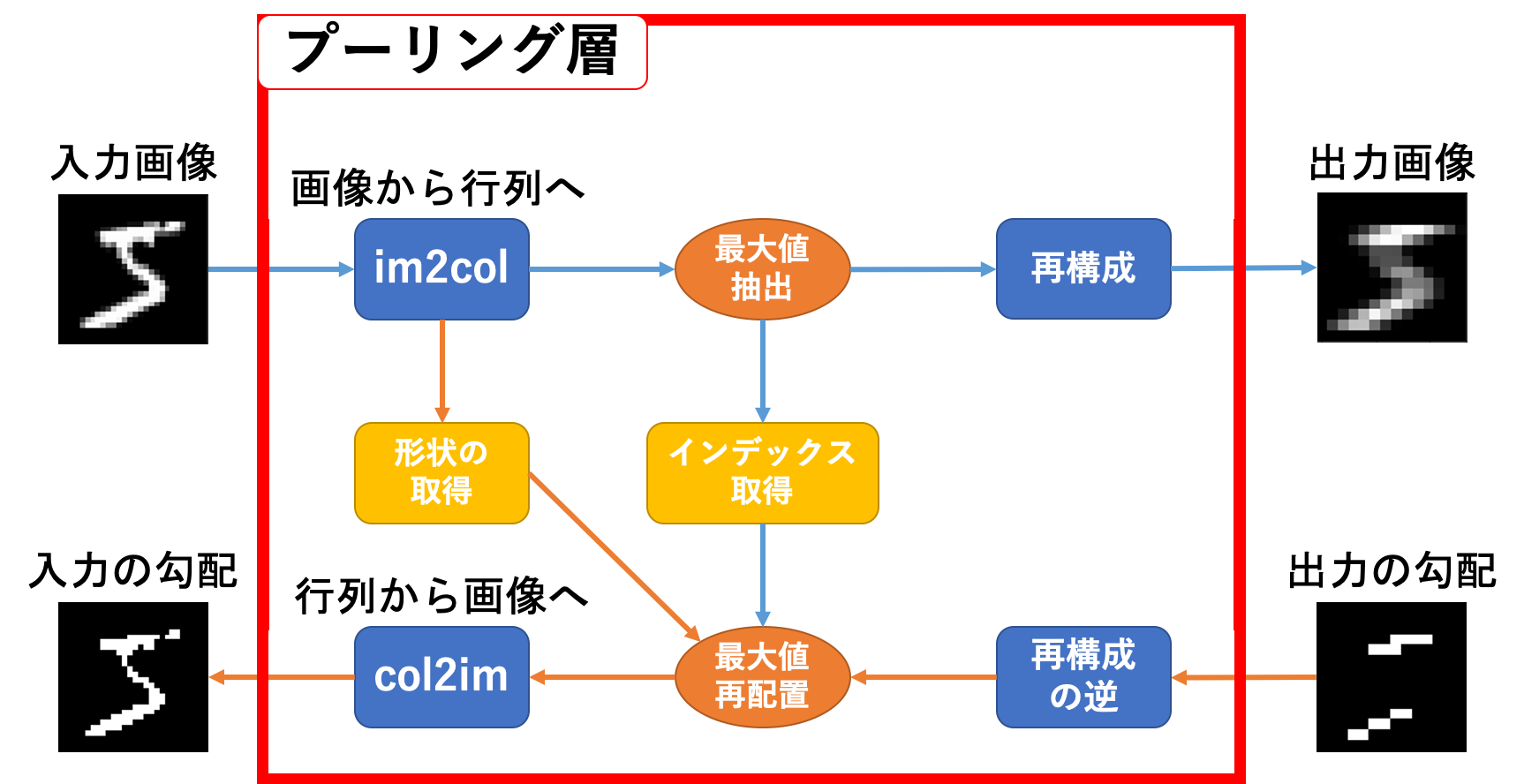
プーリング層順伝播
順伝播を見てみます。関係しているのはカラー部分です。
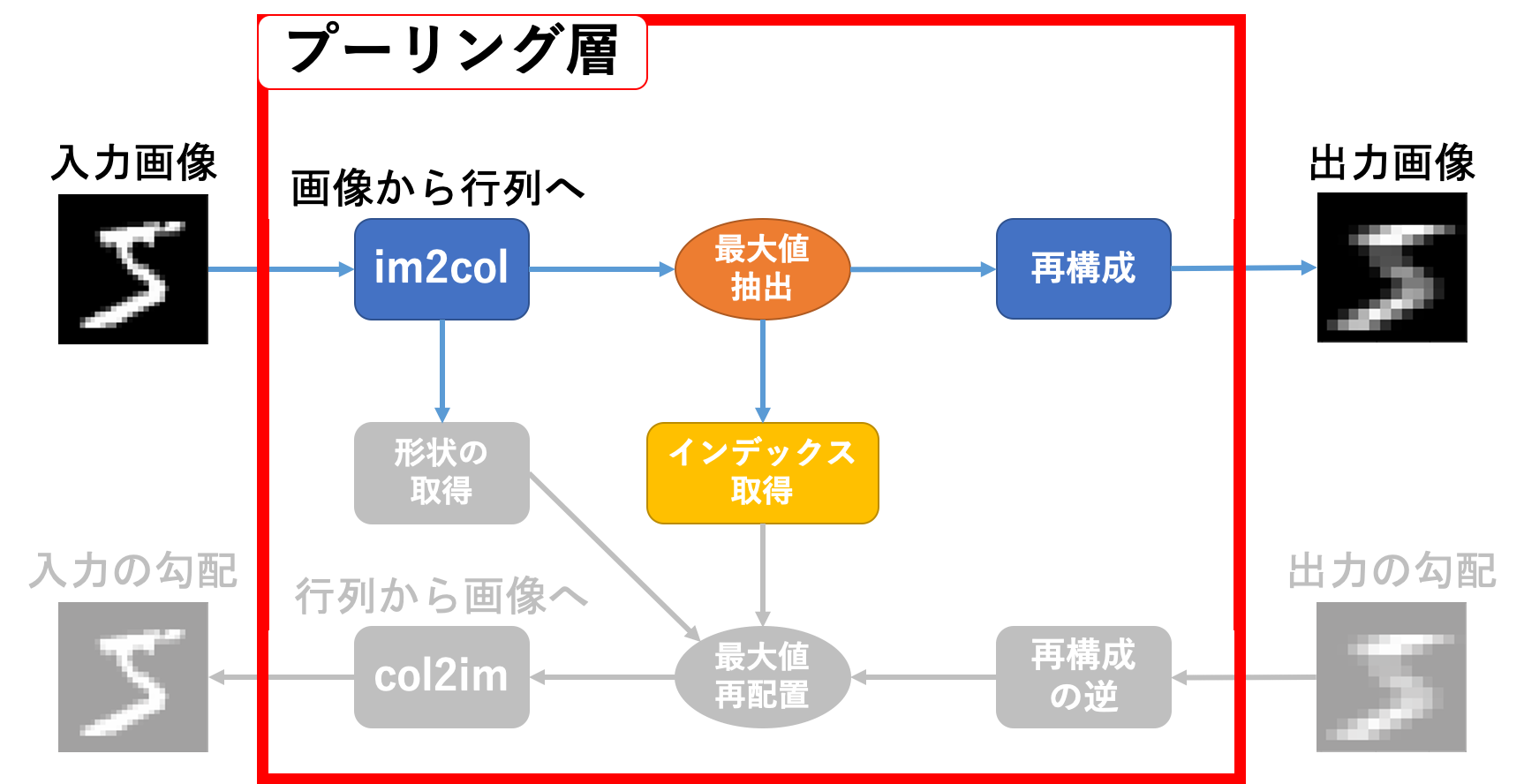
動作としては
- 入力画像を
im2col関数に投げる - 返り値の形状を取得する
- 返り値から最大値とそのインデックスを取得する
- 出力画像の形状に再構成する
という感じです。逆伝播のためにいくつか保持しておくべきものがありますね。
詳しく見ていきます。目標とする動作は下図の通りです。
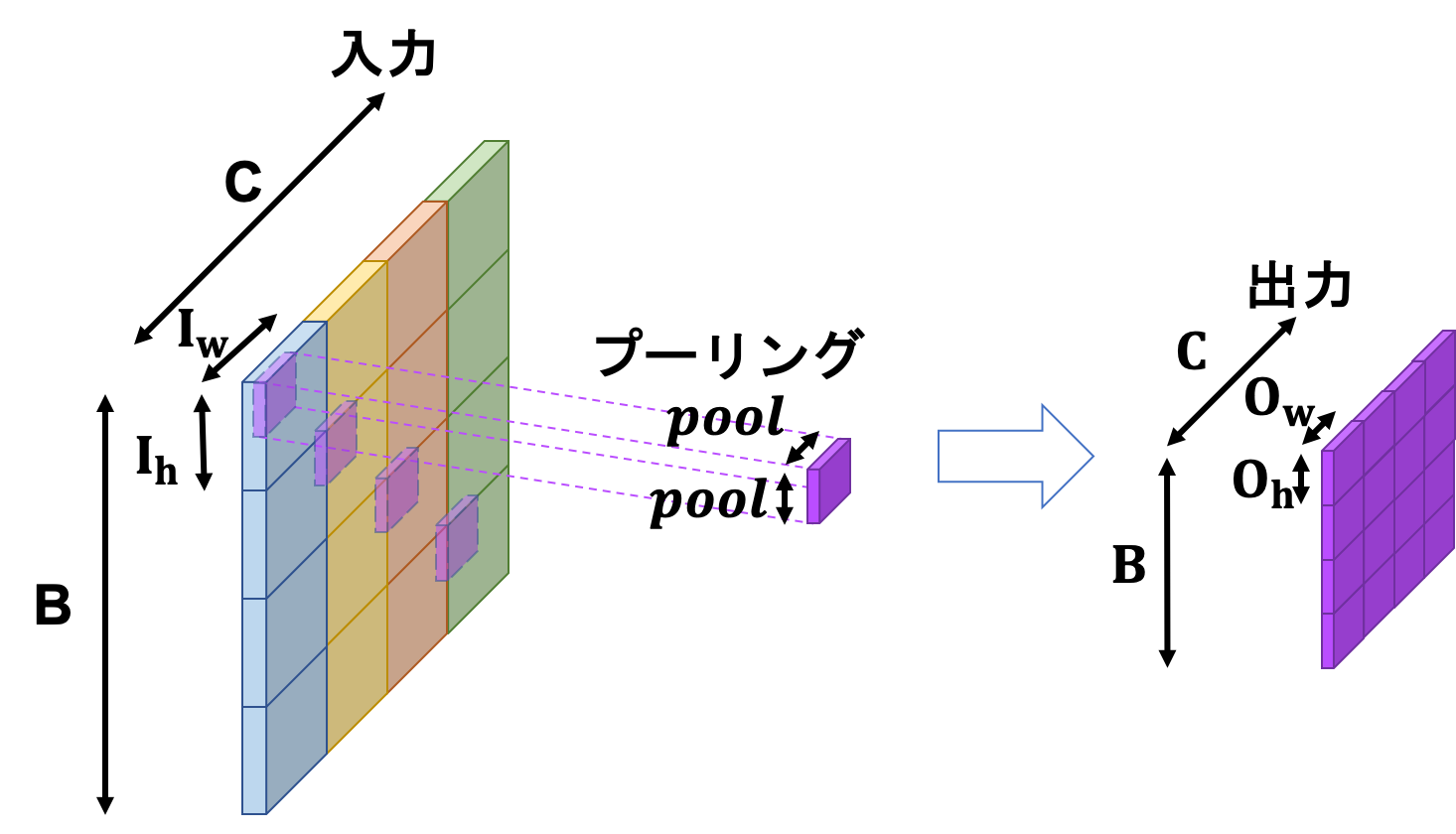
まず、入力テンソルをim2col関数に投げて2次元行列に変換します。
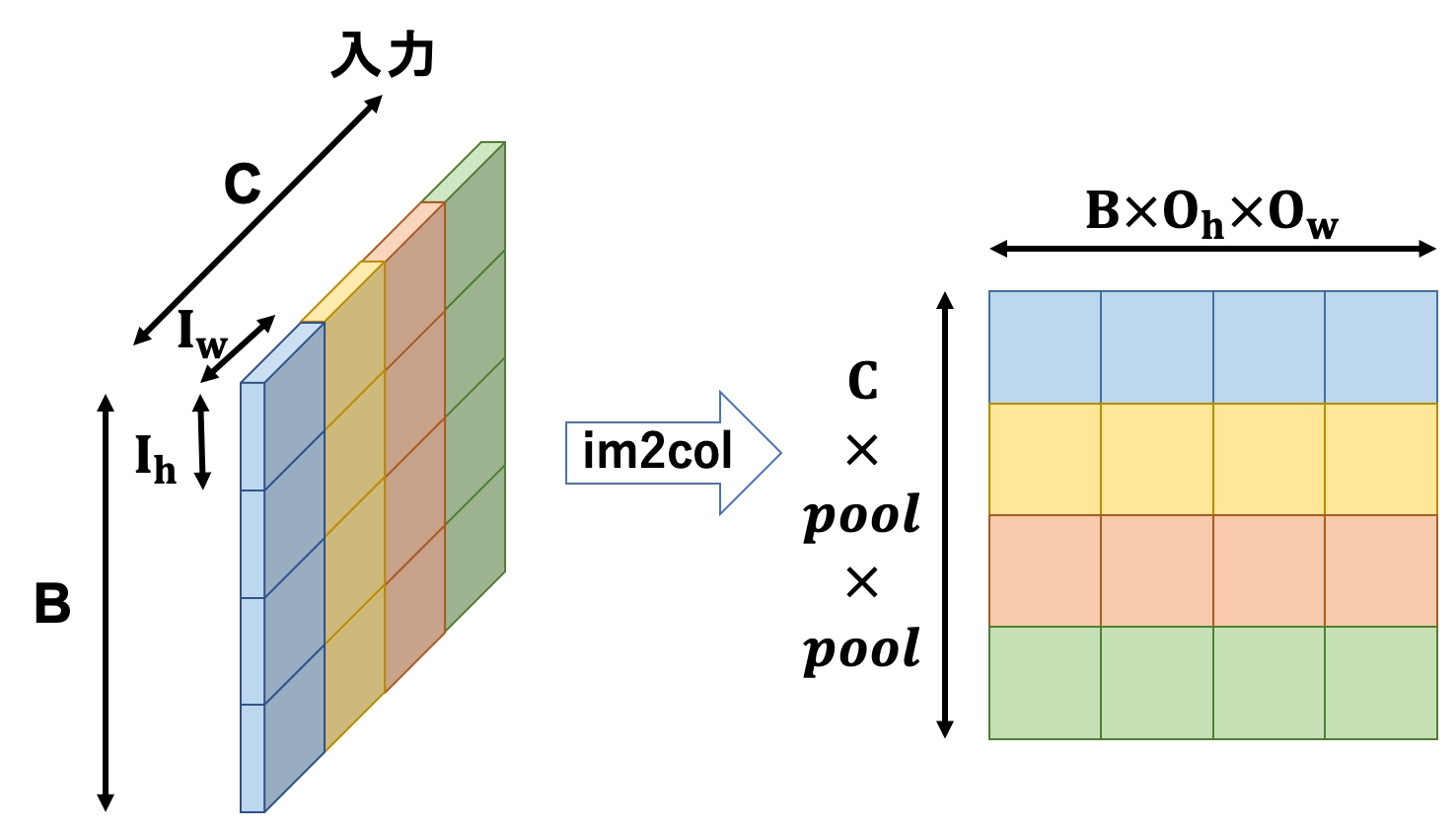
さらにこの2次元行列を変形します。
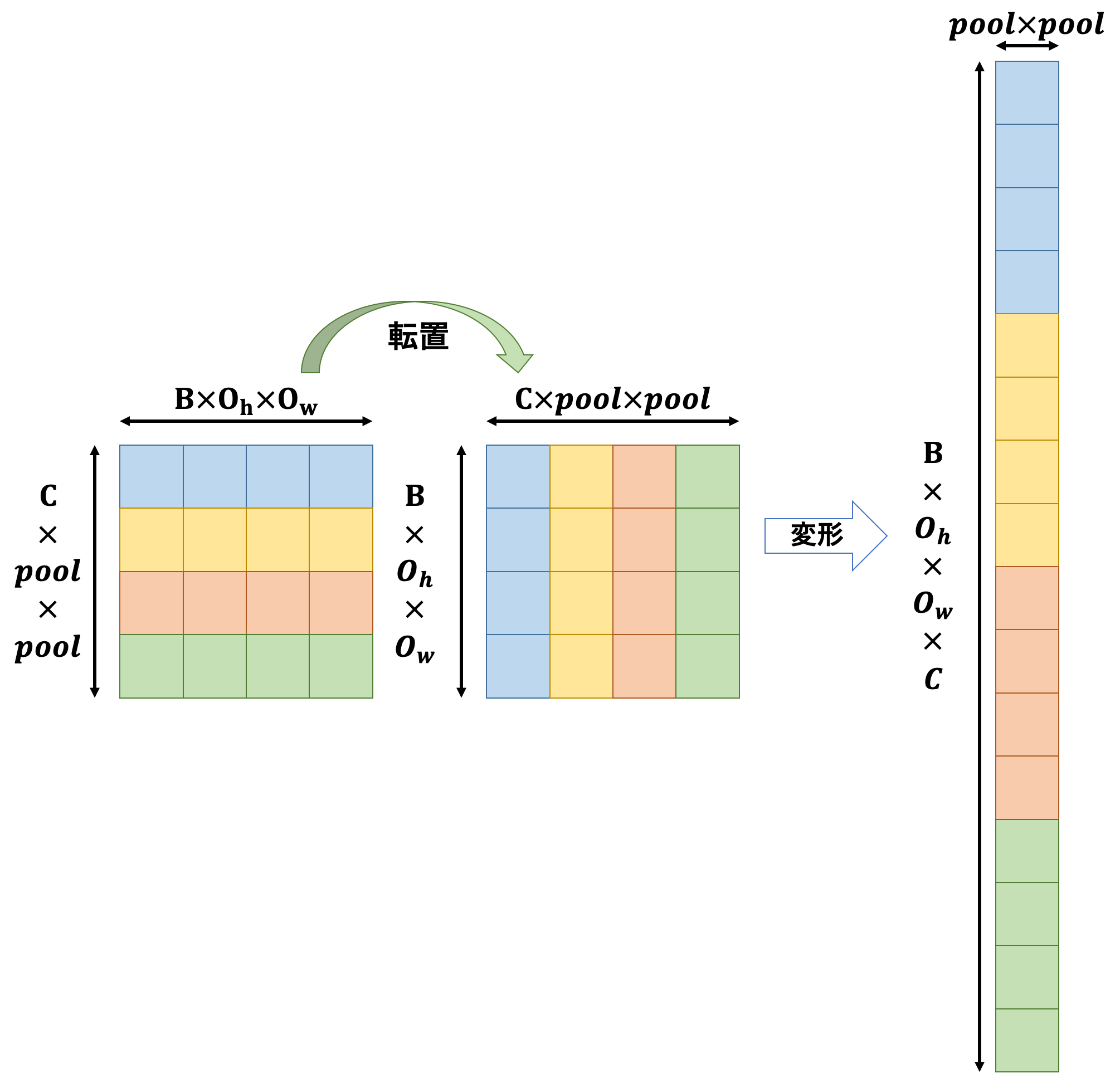
このような縦長な行列に変形した後は列方向に和を取り、最後に変形と次元入れ替えを行えば出力の完成です。
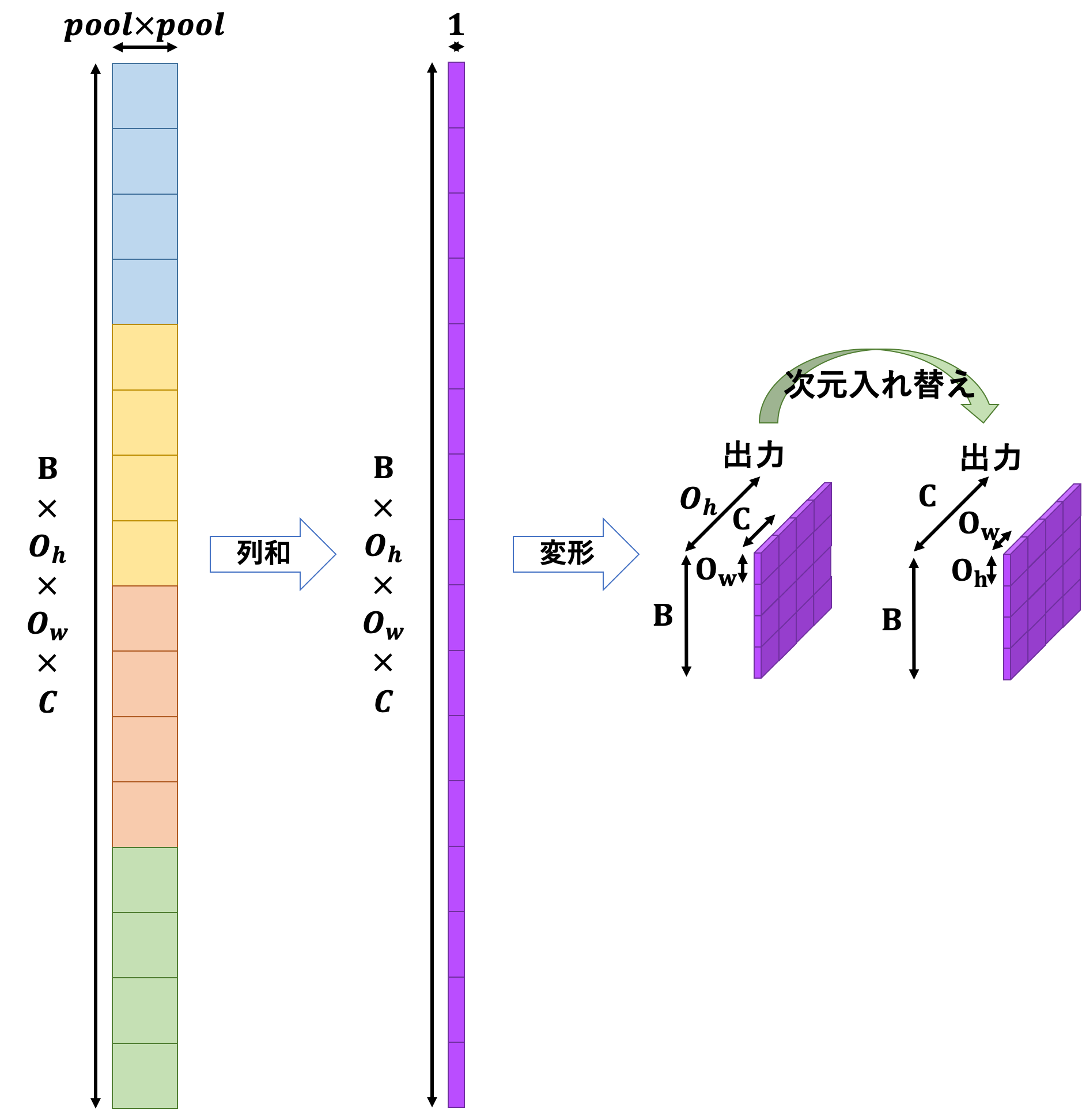
また、列和を取る前に最大値のインデックスを取得しておく必要があります。
プーリング層逆伝播
続いて逆伝播です。関係しているのは数のカラー部分ですね。
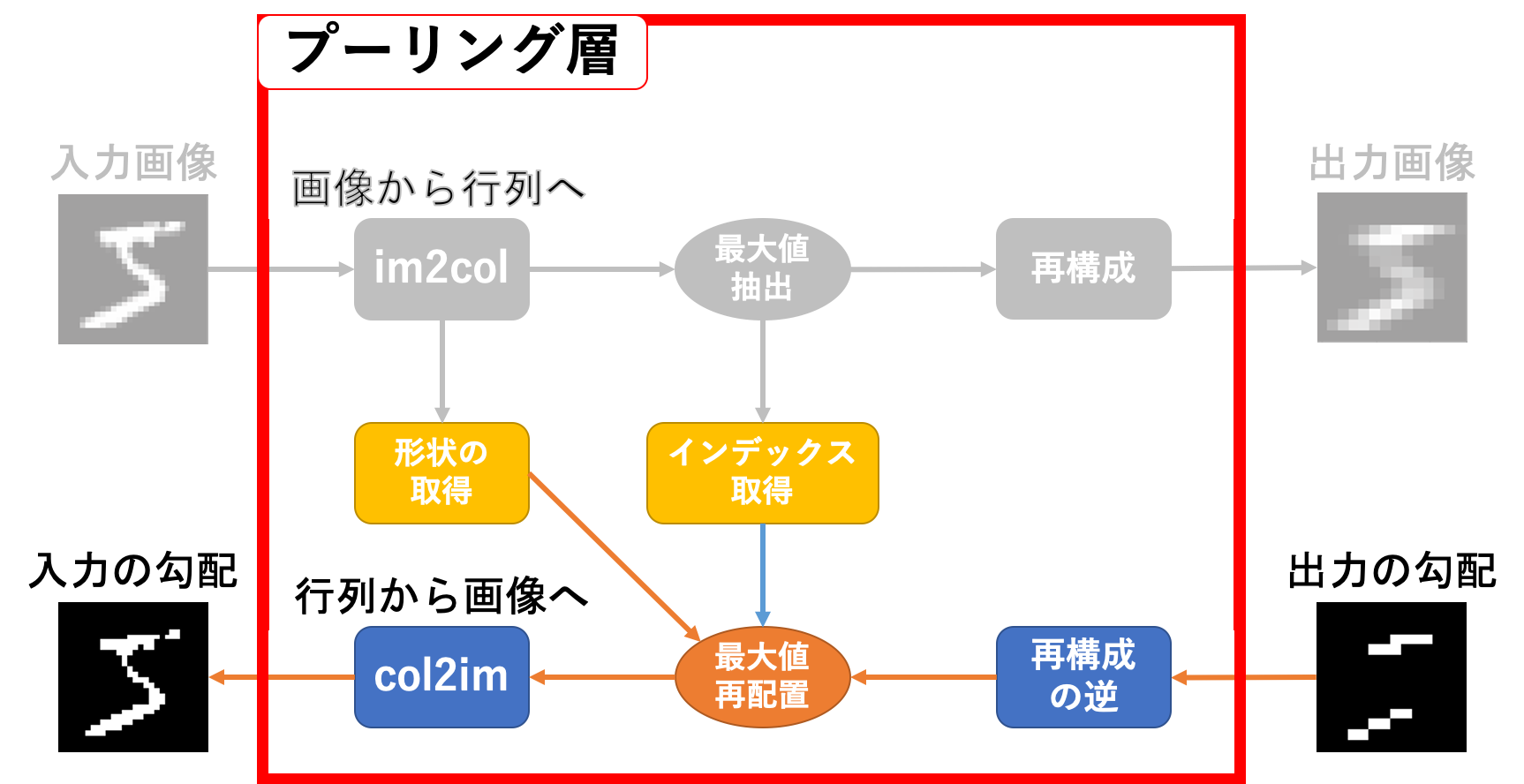
動作としては
- 出力画像の勾配を変形する
- 入力画像を
im2col関数に投げた時の返り値と同じ形状の空の行列を生成する - 生成した空の行列の、元の返り値の最大値があったインデックスに勾配情報を配置する
-
col2im関数に投げる
という感じです。ちょっと言葉だけでは動作が分かりにくいですね…以下のような感じです。
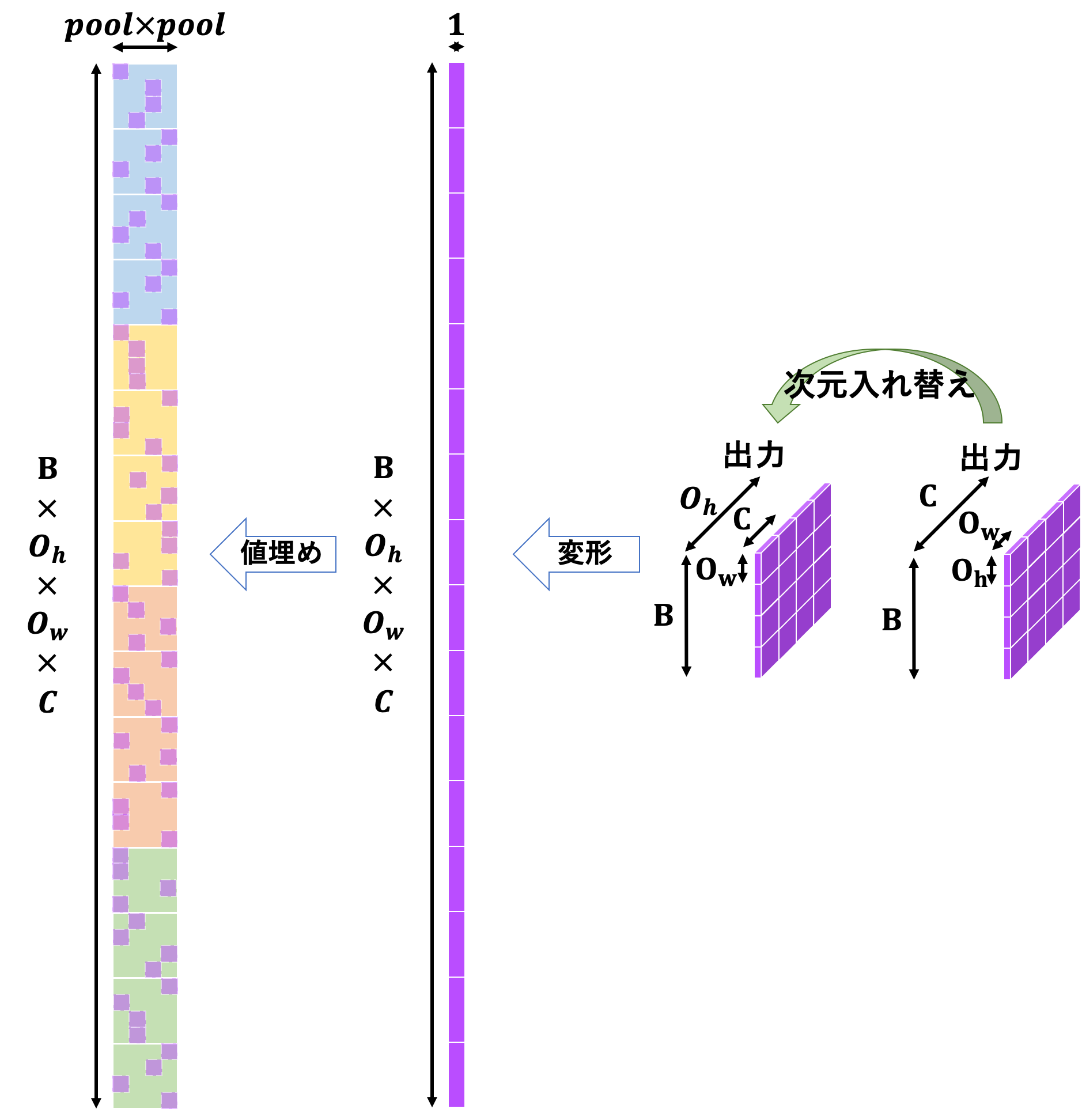
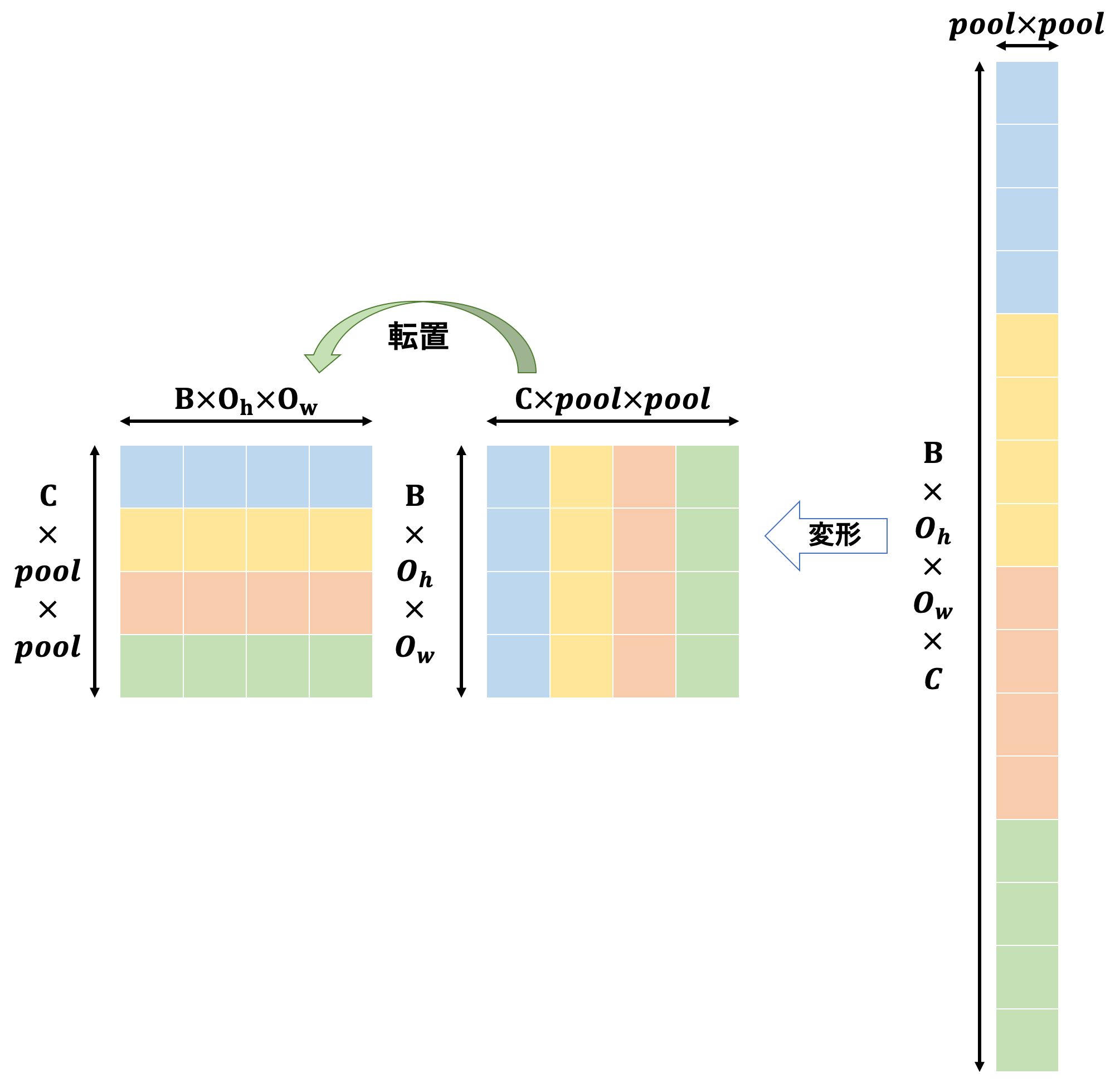
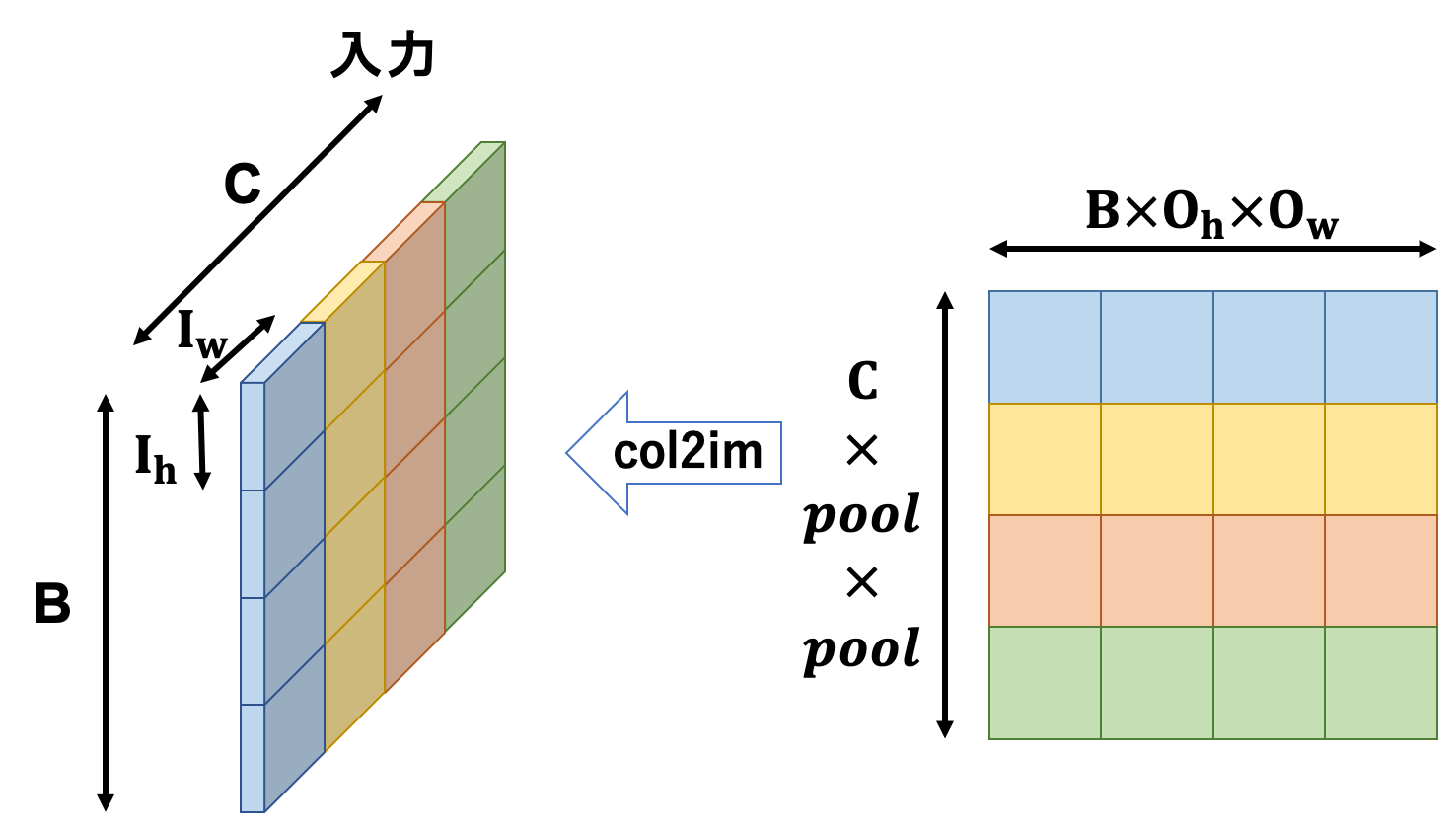
プーリング層学習
設計図にないのでお分かりかと思いますが、プーリング層に学習すべきパラメータは存在しません。ということで学習することもありません。
プーリング層実装
プーリング層の説明は畳み込み層と比べて随分簡単でしたね。実装もそこまで複雑なことはしません。
pool.py
import numpy as np
class PoolingLayer(BaseLayer):
def __init__(self, *, I_shape=None,
pool=1, pad=0,
name="", **kwds):
self.name = name
if I_shape is None:
raise KeyError("Input shape is None.")
if len(I_shape) == 2:
C, I_h, I_w = 1, *I_shape
else:
C, I_h, I_w = I_shape
self.I_shape = (C, I_h, I_w)
_, O_shape, self.pad_state = im2col(np.zeros((1, *self.I_shape)), (pool, pool),
stride=pool, pad=pad)
self.O_shape = (C, *O_shape)
self.n = np.prod(self.O_shape)
self.pool = pool
self.F_shape = (pool, pool)
def forward(self, x):
B = x.shape[0]
C, O_h, O_w = self.O_shape
self.x, _, self.pad_state = im2col(x, self.F_shape,
stride=self.pool,
pad=self.pad_state)
self.x = self.x.T.reshape(B*O_h*O_w*C, -1)
self.max_index = np.argmax(self.x, axis=1)
self.y = np.max(self.x, axis=1).reshape(B, O_h, O_w, C).transpose(0, 3, 1, 2)
return self.y
def backward(self, grad):
B = grad.shape[0]
I_shape = B, *self.I_shape
C, O_h, O_w = self.O_shape
grad = grad.transpose(0, 2, 3, 1).reshape(-1, 1)
self.grad_x = np.zeros((grad.size, self.pool*self.pool))
self.grad_x[:, self.max_index] = grad
self.grad_x = self.grad_x.reshape(B*O_h*O_w, C*self.pool*self.pool).T
self.grad_x = col2im(self.grad_x, I_shape, self.O_shape,
stride=self.pool, pad=self.pad_state)
return self.grad_x
def update(self, **kwds):
pass
おわりに
CNNの実験コード組んでみたら上手く動かず、ずっと調査してました...結論から言うと畳み込み層もプーリング層も問題なく、活性化関数が問題だったんですけどね泣笑
活性化関数一覧の方の実装も変更してあります。
次回記事で実験コードを載せます。LayerManagerクラスなども結構変更してたりします。