【初心者】機械学習のクラスタリングを調べてみた

背景・目的

私は、現在データエンジニアリングを生業としています。普段は、データ基盤の構築や、パフォーマンスチューニングなどビックデータに関する業務に従事しています。
ビックデータの収集や、蓄積、分析などの環境構築の経験はそこそこありますが、機械学習による予測や分類などのスキルは持ち合わせていませんでした。
今まで機械学習を避け続けてきましたが、一念発起し学ぼうと思います。

学び方としては、AWS Certified Machine Learning – Specialty（以降、ML試験という。）の勉強を通して、理解を深めていきます。ML試験のガイドの第２分野に、探索的データ解析が登場しましたのでそこから学びたいと思います。

今回は、クラスタリングについて学びたいと思います。

2.3 機械学習のデータを分析および視覚化する
・クラスタリング (階層型、診断、エルボープロット、クラスターサイズ

なお、過去の機械学習の調べてみたシリースは下記にまとめています。

• 2.探索的データ分析
• 2.1.モデリング用のデータをサニタイズおよび準備する
  • 【初心者】探索的データ解析とは何かを調べてみた
  • 【初心者】データのスケーリングを調べてみた
  • 【初心者】データの拡張を調べてみた
  • 【初心者】データアノテーションを調べてみた
• 2.2.特徴エンジニアリングを実行する
  • 【初心者】特徴量エンジニアリングについて調べてみた
  • 【初心者】特徴量エンジニアリング（データのビニング）について調べてみた
  • 【初心者】特徴量エンジニアリング（トークナイゼーション）について調べてみた。
  • 【初心者】特徴量エンジニアリング（外れ値）について調べてみた
  • 【初心者】特徴量エンジニアリング（合成データ）について調べてみた
  • 【初心者】特徴量エンジニアリング（ダミー変数[One-Hotエンコーディング]）について調べてみた
  • 【初心者】特徴量エンジニアリング（次元低減）について調べてみた
• 2.3 機械学習のデータを分析および視覚化する
  • 【初心者】機械学習のデータを分析および視覚化を調べてみた
• 機械学習プロセス
  • 【初心者】AWS Machine Learning Lensを整理する

まとめ

• クラスタは分類とは違う。分類。事前に箱が決まっており、どこに入れるか。クラスタリングはデータから箱を決める。
• クラスタには、各データが1つのグループに属するものをハードクラスタリング、複数に属すものがソフトクラスタリングという。
• クラスタを使うことで、マーケティングのセグメンテーションで利用したり他社との差別化、テストマーケに利用できる。

概要

機械学習のクラスタリングとは？メリットや具体的な手法について解説を参考に整理します。ありがとうございます。

クラスタリングとは？

• clustering
• 教師なし学習の一種。その中でも一般的な学習手法。
• 分類とは違う。
  • 分類は教師あり学習なので、常にどのグループに所属するかの答えをもとに学習したモデルを使う。答えが未知のデータの所属先を予測する。
  • クラスタリングは教師なしの学習で行うため、データのもとに特徴を学習した上でグループ分けする。

分類。事前に箱が決まっており、どこに入れるか
クラスタリング。データから箱を決める。

• クラスタリングの種類
  • ハードとソフトの二種類ある。それぞれの意味は以下の通りです。
    • それぞれのデータが単一グループに属することをハードクラスタリング
    • それぞれのデータが複数のグループに属することをソフトクラス他リング

クラスタリングの手法を導入するメリット

• データの特徴や構造を捉える手法として非常に有用
• マーケティングをはじめとする営利活動以外にも、天文学や考古学などのアカデミックな分野でも活用されているとのことです。

1.最適なターゲット市場を選定できる

• マーケティングの基本的な考え方の一つにセグメンテーションがあります。
  • 顧客の性別や年齢、趣味、嗜好などにしたがって顧客市場を細分化すること。
  • 顧客をセグメントに分類し、自社製品に見合ったグループに訴求することは効果的なマーケティング戦略になる。
• セグメンテーションの実施にはクラスタ分析がよく利用される。
• 顧客が持つどの属性をセグメンテーション変数として使うのがよいかは、分析の目的に合わせて選別する必要がある。

2.競合に対して差別化戦略を行える

• 新製品の企画開発や市場投入にあたって、企業はキャンペーンなどさまざまな施策を行う。
  • 競合他社の製品や市場の調査が不可欠だが、クラスタリングはそのような分析にも応用することが可能。
  • 分析にかけたのち、自社の新製品と他社の既存の商品が同じクラスタに分類された場合、自社製品の新規性を打ち出すなど、差別化戦略を取る必要が出てくる。
  • 反対にクラスタリングを行うことでまだどの企業も参入していない、空白のマーケットを発見することも可能。

3.効果的なテストマーケットの実施

• 多くの企業はマーケティング施策などを実際に行う前段階として、テストマーケットにて施策の事前評価を行うことが一般的。
  • テストマーケットの選定はマーケティング施策の成否を決める重要なプロセス。
  • クラスタリングはこのような場合にも応用することが可能。
  • 形成された各クラスタからテストマーケットを選出することで、それぞれのマーケット間の異質性とテストの網羅性を担保し、効果的なテストが実現できる。

階層的クラスタリング

• 階層クラスター分析とは、集合体のデータのうち、最も似ている組み合わせから先にまとめていく階層的手法。

1.群平均法

• 2つのクラスターに属している対象の間のすべての組み合わせの距離を計算し、それらの平均値をクラスタ間の距離として決める手法。

2.ウォード法（最小分散法）

• すでにあるクラスターの中で、1番距離の近い2つのクラスターが選ばれ、1つのクラスターに結合されていく操作を、目標のクラスター数になるまで続ける。

3.最短距離法

• 最短距離法は単連結法とも呼ばれる。
• 2つのクラスタ間で一番近いデータ同士の距離を、クラスタ間の距離として採用する手法。
• 群平均法と同様に、クラスタを構成する要素同士の距離をすべて求め、その中で一番距離の短い組み合わせを選ぶことでクラスタ間の距離として求める。
• この方法のメリットはウォード法などと比較した場合に、計算量が少なくなるが、同時に外れ値に弱いというデメリットもあります。

4.最長距離法

• 最短距離法とは反対に、クラスタを構成する要素同士の距離の中で最長のものをクラスタ間の距離として採用する。

非階層的クラスタリングの手法

• 非階層クラスタリングは、階層を作らずにデータをグルーピングしていく手法。
• 母集団の中で近いデータを収集し、指定された数のクラスタに分類する。
• クラスタを形成した後で自由にクラスタを分けることができないため、事前にクラスタ数を指定する必要がある。

クラスタリングが活用できる事例

1.ECサイトの顧客分析

• ECサイトなどにおける顧客分析
• CRMや広告出稿を行う際、CVRを最大化するために、最もよく使われる分析手法
• ユーザーに自社の商品を販売するにあたり、特定の属性を持つユーザーにどの施策が適切かを把握しておけば、高い効果が期待できる。

2.画像の減色処理

• k-means法を活用することで画像の代表色を指定し、減色処理を実行することで容量を削減することができる。

実践

AI Academy Mediaのk-meansとはを元に手を動かしていきます。ありがとうございます。

K-meansとは

• クラスタリングのアルゴリズムの一種で実行速度が速く拡張性があるとのことです。
• Kは必ずデータの数より小さい値に設定します。なぜ「Kがデータは数より少なく設定するのか」ですが、クラスの数＜データ数として、分類をするためです。

データの作成

import numpy as np
from sklearn.cluster import KMeans
from sklearn import metrics
import matplotlib.pyplot as plt

1次元目をx1，2次元目をx2とする行列を作成します。

x1 = np.array([1,2,3,1,5,6,5,5,6,7,8,9,7,9])
x2 = np.array([1,3,2,2,8,6,7,6,7,1,2,1,1,3])

x = np.c_[x1, x2]

x軸とy軸の幅を設定する

plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('data')

散布図を作成

plt.scatter(x1, x2)
plt.show()

kを3に設定する

パラメータのn_clustersはクラスタ数を示している。
実行すると、それぞれのデータがどのクラスタに属しているか出力されます。

kmeans = KMeans(n_clusters=3)
kmeans_model = kmeans.fit(x)
print(kmeans_model.labels_)

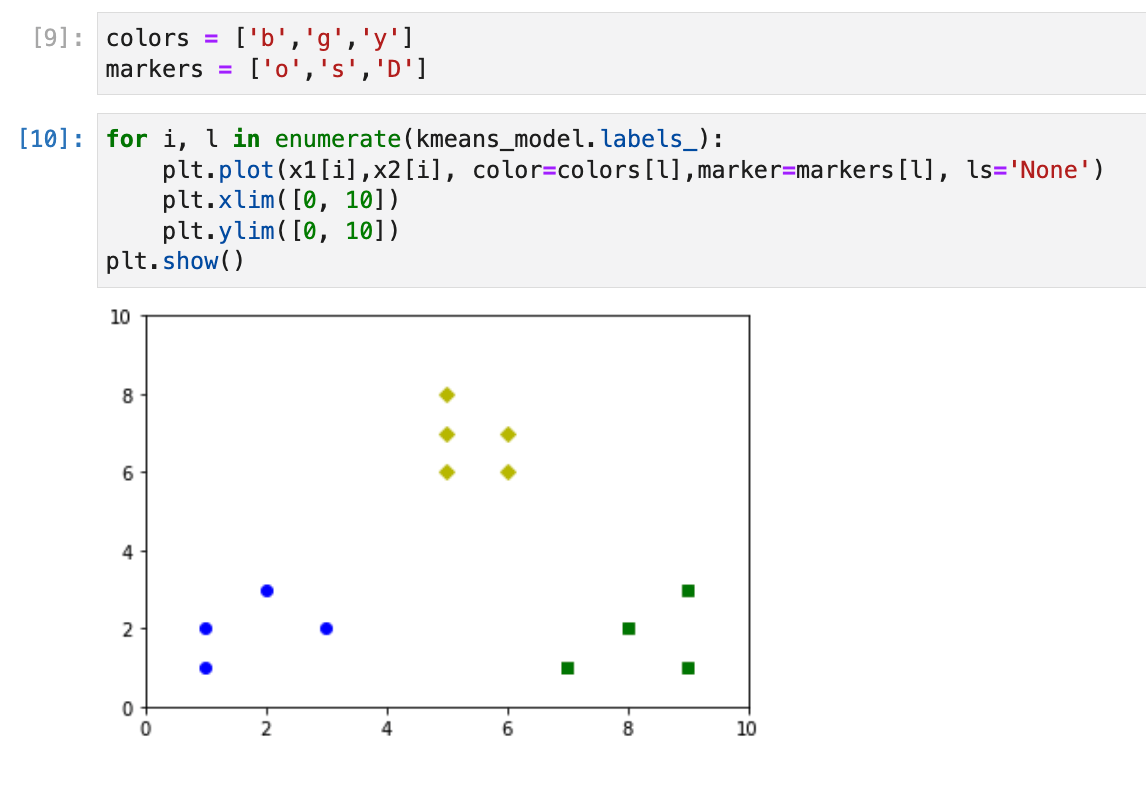
数値ではわかりづらいので可視化する。以下は、色とマーカを指定している。

colors = ['b','g','y']
markers = ['o','s','D']

for i, l in enumerate(kmeans_model.labels_):
    plt.plot(x1[i],x2[i], color=colors[l],marker=markers[l], ls='None')
    plt.xlim([0, 10])
    plt.ylim([0, 10])
plt.show()

• きれいにクラスタリングされている。

微妙な座標だとどうなるのか？

上記の例だと、データが分かりとわかりやすいが、データが近しい場合はどうなるのか気になりました。

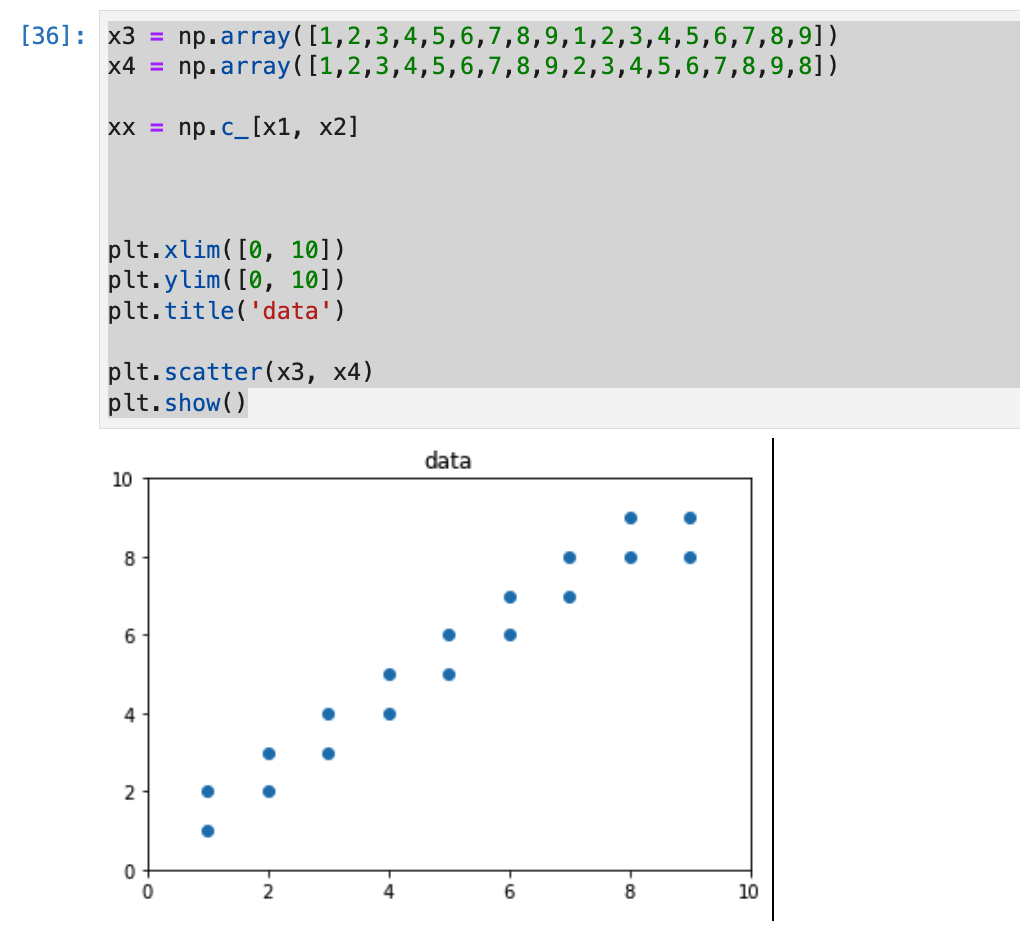
x3 = np.array([1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9])
x4 = np.array([1,2,3,4,5,6,7,8,9,2,3,4,5,6,7,8,9,8])

xx = np.c_[x1, x2]

plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('data')

plt.scatter(x3, x4)
plt.show()

kmeans = KMeans(n_clusters=3)
kmeans_model = kmeans.fit(x)
print(kmeans_model.labels_)

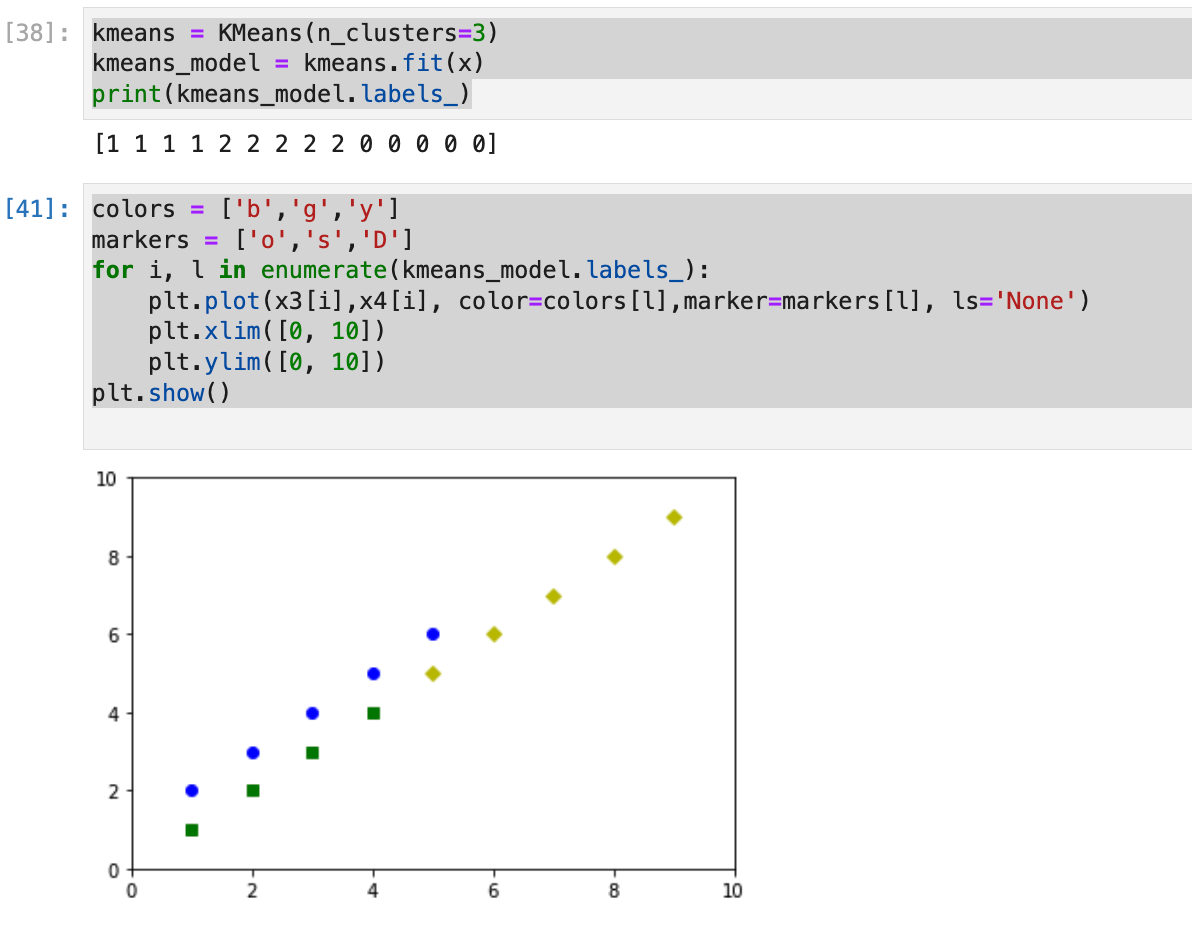
colors = ['b','g','y']
markers = ['o','s','D']
for i, l in enumerate(kmeans_model.labels_):
    plt.plot(x3[i],x4[i], color=colors[l],marker=markers[l], ls='None')
    plt.xlim([0, 10])
    plt.ylim([0, 10])
plt.show()

• 直線で分類されたようです。

考察

• 今回は、クラスタリングを学びました。実装では、クラスタリングの手法の一つであるk-meansを学びました。
• 他にもクラスタリングの手法はあるので、今後試してみたいと思います。

参考