背景・目的
私は、現在データエンジニアリングを生業としています。普段は、データ基盤の構築や、パフォーマンスチューニングなどビックデータに関する業務に従事しています。
ビックデータの収集や、蓄積、分析などの環境構築の経験はそこそこありますが、機械学習による予測や分類などのスキルは持ち合わせていませんでした。
今まで機械学習を避け続けてきましたが、一念発起し学ぼうと思います。
学び方としては、AWS Certified Machine Learning – Specialty(以降、ML試験という。)の勉強を通して、理解を深めていきます。ML試験のガイドの第2分野に、探索的データ解析が登場しましたのでそこから学びたいと思います。
今回は、以下のうち次元低減について学びたいと思います。
特徴エンジニアリングの概念を分析/評価する (データのビニング、トークナイゼーション、外れ値、合成的特徴、One-Hotエンコーディング、次元低減)
なお、過去の機械学習の調べてみたシリースは下記にまとめています。
-
2.探索的データ分析
-
2.1.モデリング用のデータをサニタイズおよび準備する
-
2.2.特徴エンジニアリングを実行する
-
機械学習プロセス
まとめ
- 次元低減=次元削減
- 次元削減の手段の一つとして主成分分析がある。
- 主成分分析では、特徴量を抽出し次元数を減らす。次元を減らすことにより可視化が可能になる。
概要
次元低減とは?
キカガクさんの機械学習 実践(教師なし学習)を参考に整理しています。ありがとうございます。
次元削減とは、例えば 4 次元のデータ(列数が 4 つのデータ)があった場合、2 次元などの低次元に落とし込むことを指します。また、一般的に次元削減は単にデータを削除するのではなく、可能な限り元のデータの情報を保持したまま、低次元のデータに変形を行います。
以降、次元低減を次元削減と読み替えています。
- 次元削減は、その名の通り次元数を削減することを指します。
- データを削除するのではなく、可能な限り元のデータの情報を保持したまま低次元データに変形する。
次元削減の1つの手法として、主成分分析がある。
主成分分析とは?
次元削減とは?次元削減と主成分分析に関して学ぼう!の内容も参考しています。ありがとうございます。
定義を以下に整理します。
- Principal Component Analysis(PCA)
- 主成分分析では、特徴量を抽出することによって、データセット内の特徴量を削減することができる。
- 高次元(多次元)データを低次元化する手法
- 低次元化することにより可視化もできる。(可視化するための手法。)
- 教師なし学習の一つ
- 特徴量を選択するのではなく、抽出する。
- 抽出は、非可逆的なもの。(元のデータセットの特徴量には戻らない。)
- 分散により次元の重要度を決める。
- 分散が大きいほどデータのばらつきは大きい
- 分散が小さいほどデータのばらつきは小さい
${例) y=2x+1}$の1次関数で考える。
※出典:次元削減とは?次元削減と主成分分析に関して学ぼう!から抜粋
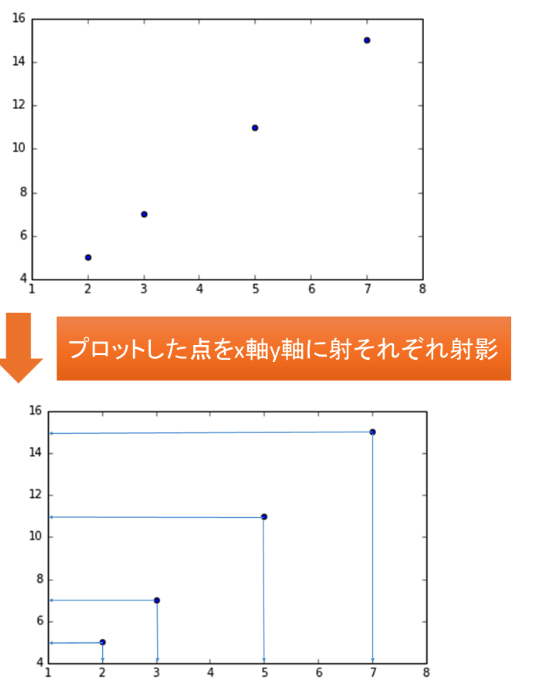
主成分分析する前の分散について考えると、
x軸に射影したときの分散は、3.69(3.6875)、y軸に射影したときの分散は14.75。
※ 参考
それぞれのxとyが相関していることは明らかであるため、2次元から1次元への圧縮を考える。
新しい次元Z1は以下のとおりです。

※出典:次元削減とは?次元削減と主成分分析に関して学ぼう!から抜粋
- 新しく抽出した次元に射影したデータの分散は、x軸y軸へ射影したときよりも間隔(ばらつき)が大きいので分散が大きいことが分かる。
さらに、この次元に直行する新しい次元についても考える。
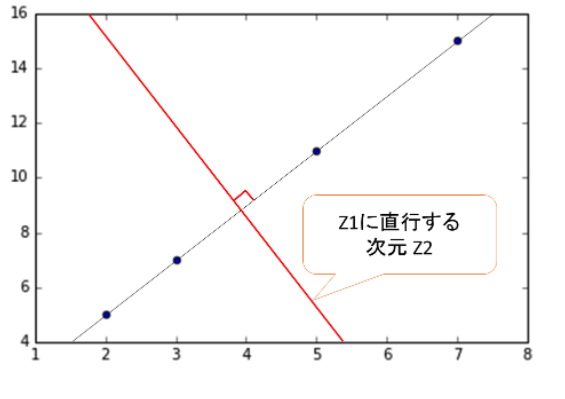
※出典:次元削減とは?次元削減と主成分分析に関して学ぼう!から抜粋
- この次元では全てのデータの間隔(ばらつき)が0なので、情報が全く含まれていないことが分かる。
以下は、キカガクさんの説明を載せています。こちらも合わせて見ると少し理解が深まりました。
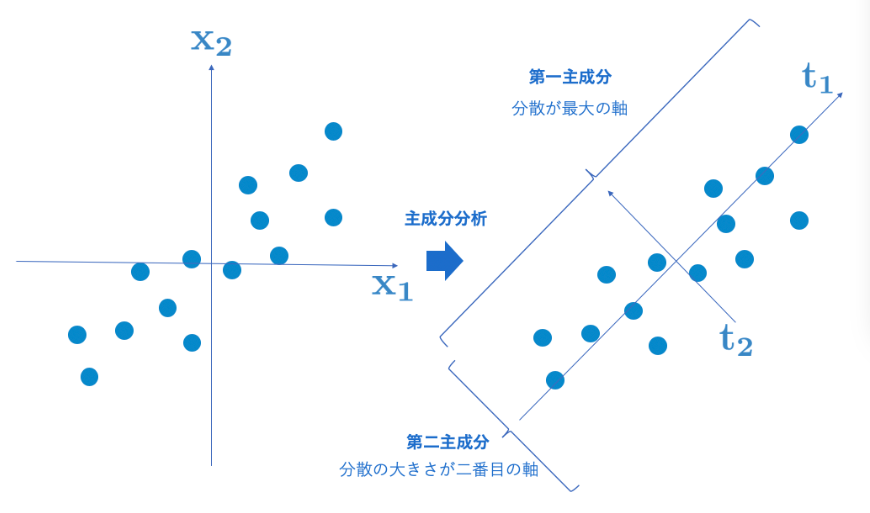
※出典:機械学習 実践(教師なし学習)から抜粋
さらに、こちらの記事がとてもわかり易かったです。ありがとうございます。
散布図にそれっぽい線(軸)を引くこと
この線は、データのばらつき、すなわち分散を最大にするように引かれています。
- 第一主成分軸が、ばらつきが最大化される、第二主成分軸が、ばらつきが2番目に大きい。
この線が引っ張れると、とてもうれしいことがあります。
それは「データを一つ一つ見なくても、データの概要をつかむことができる」ことです。
主成分分析ができると、データの要約ができます。
- データの要約ができて、ぱっと見で分かる。
主成分分析ですと、様々な要素をひとまとめにできるので、例えば「収入が多く購買意欲も高いユーザー」など複数の要素を組み合わせて一つのカテゴリとして扱うことができるようになります。
- 〇〇✕△△の組わせで1つのカテゴリとして扱える。
主成分分析の結果はどのように解釈すればよいか
まず『データの要約』という観点から見ると、主成分軸の「寄与率」を理解することが重要です。
寄与率とは、下の図のように「この主成分軸一つで、データの何割を説明することができているか」を表したものです。
- 主成分分割の解釈の一つは寄与率がある。寄与率は、主成分軸の1つでデータの何割を説明することができるか。
実践
データセットの準備
scikit-learnのIrisのデータセットを使用します。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
データセットを確認します。
dataset = load_iris()
x = dataset.data
t = dataset.target
feature_names = dataset.feature_names
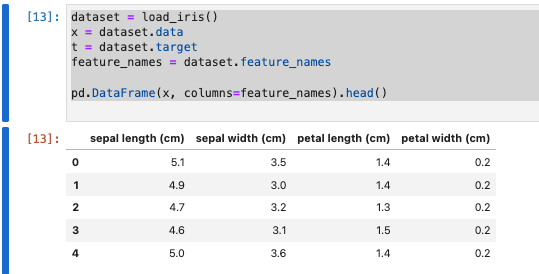
pd.DataFrame(x, columns=feature_names).head()
- データを見ると4次元ということが分かります。これを2次元に落とし込みます。
モデルの定義と学習
from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=0)
- n_componentsは次元削減後の次元数とのこと。
- 4次元から2次元に落とし込むため、パラメータは2を指定しています。
- なお、2次元にすることで可視化も可能になります。
モデルの学習では、主成分分析を適用するために必要な分散を求めます。教師なし学習では正解となる指標がないため、主成分分析では実測値の分散を用いて求めます。
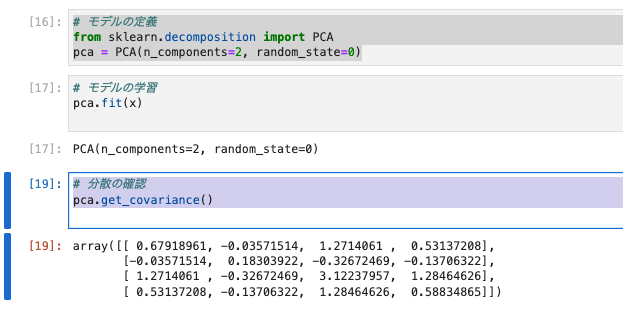
pca.fit(x)
# 分散の確認
pca.get_covariance()
- scikit-learnでは
.fit()メソッドで分散を算出する。n_components=2としているので第二主成分まで出力します。
変換
データを変換(写像)するには.transformメソッドを使用します。
写像とは、元のデータを主成分軸上へと写すことをいう。
以下の図は、写像のイメージです。わかりやすい。
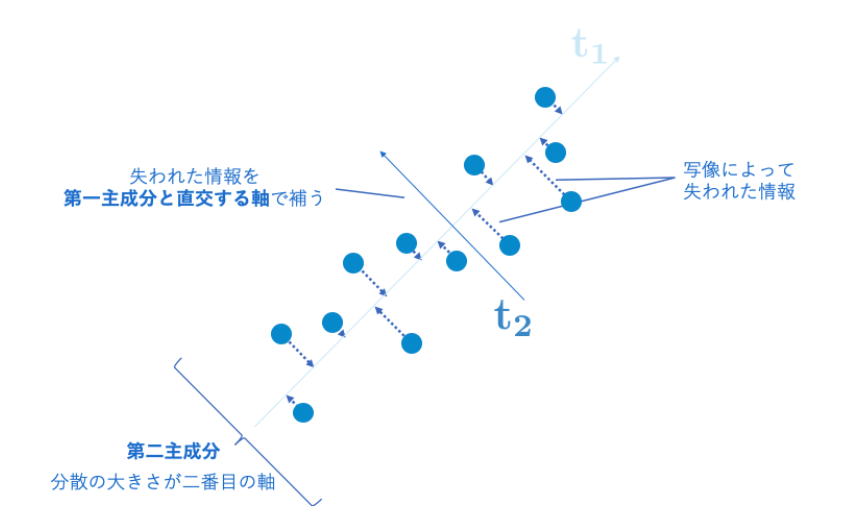
※出典:次元削減とは?次元削減と主成分分析に関して学ぼう!から抜粋
-
transformにより、第一主成分と第二主成分に写す。
主成分分析を適用します。
x_transformed = pca.transform(x)
主成分分析適用後のデータの確認します。
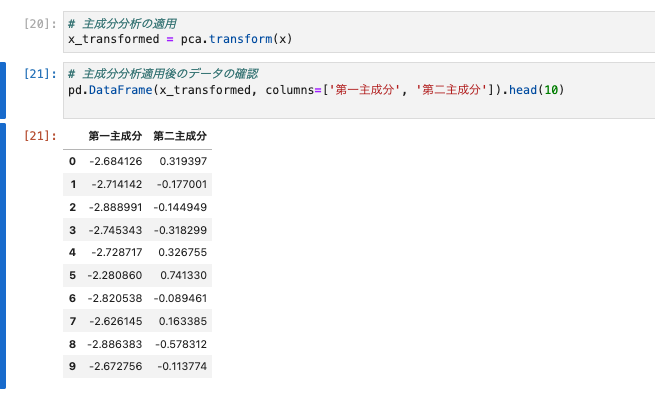
pd.DataFrame(x_transformed, columns=['第一主成分', '第二主成分']).head(10)
- データが二次元に落とし込まれることが分かりました。
- 1列目のデータが第一主成分、2列目のデータが第二主成分とよびます。それぞれの列は次元削減前の情報を持ち、それぞれの列が保持する元データの情報の割合を**寄与率(Proportion of the variance)**と呼びます。
- 寄与率は
fit()メソッド後のexplained_variance_ratio_属性からそれぞれの寄与率を確認することが出来ます。
第一主成分の寄与率:0.9246187232017271
第二主成分の寄与率:0.05306648311706782
- 第一主成分は92%、第2主成分は5%ほどの寄与率ということが分かりました。
- 97%程度の割合で、元のデータの情報を保持したまま削減できていることが確認できる。
主成分分析は100%情報を保持したまま次元削減するのではなく、いつからの情報を保持できていないことが分かる。
主成分分析を適用したあとは、この寄与率を確認し、元データをどの程度再現できているかを確認することが重要。
可視化
次元削減後のデータを可視化します。
Irisのデータセットは3種類あります。可視化を行う際に、それぞれのクラスに色を付けて表示し、次元削減後のデータを確認します。
np.unique(t)
次元削減後のデータを可視化します。
sns.scatterplot(x_transformed[:, 0], x_transformed[:, 1],
hue=t, palette=sns.color_palette(n_colors=3));
-
sns_color_palette(n_colors=3)で色を3種類に分けている。
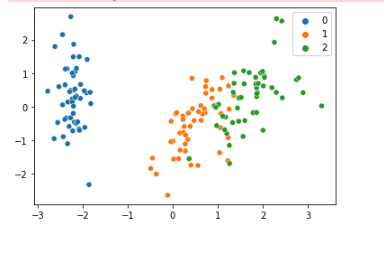
- 次元削減を行うことでデータセットを可視化することが出来ました。
- この様に可視化することにより、手元データを直感的に理解できることは重要です。
- 例えば
- クラス1(オレンジ)とクラス2(緑)は分類することは少し困難であることは想定できます。
- クラス0(青)は、機械学習を用いることなく分類を行うことも可能であることが分かる。
- 例えば
上記の関数(sns.scatterplot)でxとyの値を明示的に指定するようにとwarningが出たが、表示されたのでこのまま先に進めます。
標準化の適用
主成分分析を行う際には、必ず標準化を行うこと。標準化は平均を0、分散(標準偏差)を1とする操作。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_scaled = scaler.fit_transform(x)
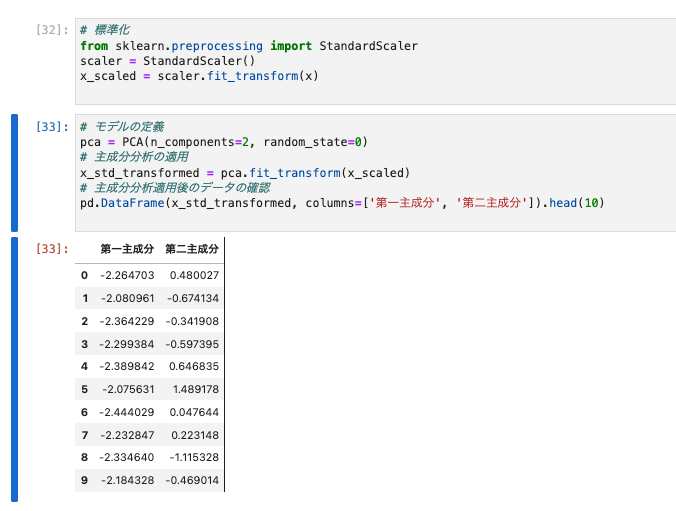
モデルの定義から主成分分析適用後のデータの確認まで行います。
pca = PCA(n_components=2, random_state=0)
x_std_transformed = pca.fit_transform(x_scaled)
pd.DataFrame(x_std_transformed, columns=['第一主成分', '第二主成分']).head(10)
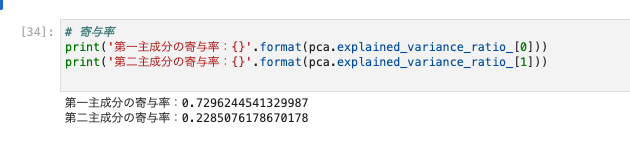
# 寄与率
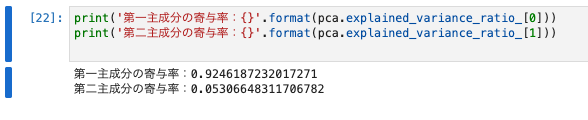
print('第一主成分の寄与率:{}'.format(pca.explained_variance_ratio_[0]))
print('第二主成分の寄与率:{}'.format(pca.explained_variance_ratio_[1]))
- 第一主成分が0.92→0.72になっている。
- 第二主成分が0.05→0.22になっている。
*全体の情報損失も大きくなっている。97%程度から94%程度の割合に減っている。
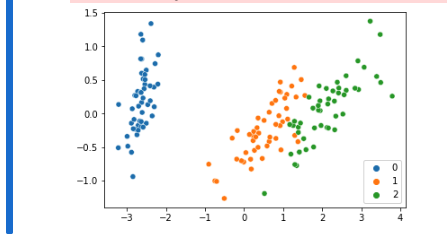
次元削減後のデータを可視化します。
sns.scatterplot(x_std_transformed[:, 0], x_std_transformed[:, 1],
hue=t, palette=sns.color_palette(n_colors=3));
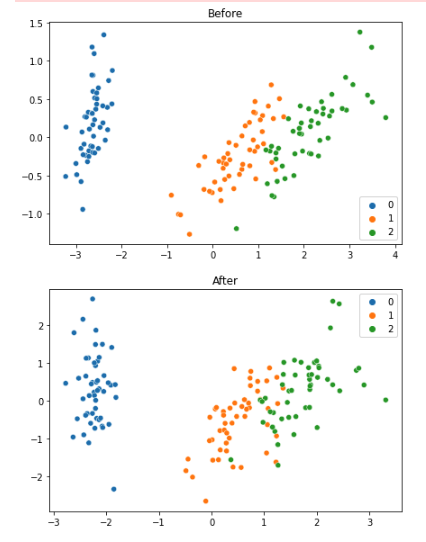
2つの結果を並べて可視化して違いを確認します。
fig = plt.figure(figsize=(7, 10))
ax1 = fig.add_subplot(2, 1, 1)
sns.scatterplot(x_transformed[:, 0], x_transformed[:, 1],
hue=t, palette=sns.color_palette(n_colors=3));
ax1.set_title('Before')
ax2 = fig.add_subplot(2, 1, 2)
sns.scatterplot(x_std_transformed[:, 0], x_std_transformed[:, 1],
hue=t, palette=sns.color_palette(n_colors=3));
ax2.set_title('After');
変換点は以下のとおりです。
- yのスケールが1.5から2に変わった。
- xのスケールが4から3に変わった。
- 1(オレンジ)と2(緑)がより近づいた。
考察
今回は、次元削減の一つの手法である主成分分析を学びました。
主成分分析は、多次元データを削減しデータを可視化するための手段と理解しました。
この他にも手法があるようなので、今後学習していきたいと思います。
参考