背景・目的

私は、現在データエンジニアリングを生業としています。普段は、データ基盤の構築や、パフォーマンスチューニングなどビックデータに関する業務に従事しています。
ビックデータの収集や、蓄積、分析などの環境構築の経験はそこそこありますが、機械学習による予測や分類などのスキルは持ち合わせていませんでした。
今まで機械学習を避け続けてきましたが、一念発起し学ぼうと思います。

学び方としては、AWS Certified Machine Learning – Specialty（以降、ML試験という。）の勉強を通して、理解を深めていきます。ML試験のガイドの第２分野に、探索的データ解析が登場しましたのでそこから学びたいと思います。

今回は、以下のうち外れ値について学びたいと思います。

特徴エンジニアリングの概念を分析/評価する (データのビニング、トークナイゼーション、外れ値、合成的特徴、One-Hot エンコーディング、次元低減)

なお、過去の機械学習の調べてみたシリースは下記にまとめています。

2.探索的データ分析
2.1.モデリング用のデータをサニタイズおよび準備する
2.2.特徴エンジニアリングを実行する
機械学習プロセス
- 【初心者】AWS Machine Learning Lensを整理する

まとめ

データセットには、外れ値が含まれる場合があり、そのまま放置するとモデルの精度に影響を与えます。そのため、外れ値を検出し、どの様に対応するかを検討する必要があります。
検出では、データセットに合わせた正しい手法を選択する必要があります。
検出のステップとしては、以下の順で進めると効率良く見つけることが出来ます。

ヒストグラム、散布図、箱ひげ図などで可視化し概要を掴む。
問題のある箇所を、四分位範囲やzスコアなどで検出する。

概要

Codexaさんの記事「外れ値とは？Pythonを使用して外れ値の検出方法を実装してみよう（全コード公開中）」を参考に整理したいと思います。

外れ値とは

外れ値（outlier）とは測定された値の中で他のデータとかけ離れているものを指します。実験結果を記録している中で、他のデータの分布とは明らかに異なる場所に数値が出現したりする際に外れ値と呼ばれることが多いです。外れ値が発生する原因は様々ですが、そのままにしておくと、データ分析の際に統計指標を歪める可能性があるため、何らかの対処が必要な場合があります。図1と図2のグラフは外れ値が存在する典型的な例です。

測定された値の中で、他のデータとかけ離れているものを指す。
データ分析の際に統計指標を歪める可能性がある。対処が必要。
例を以下に記載します。

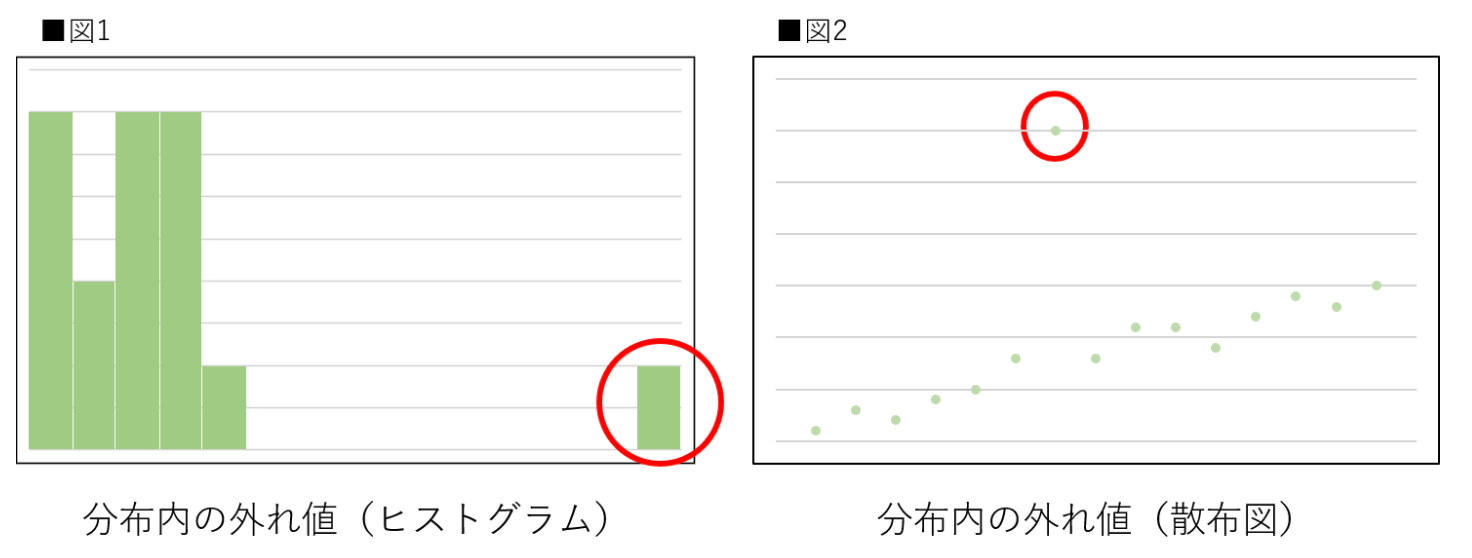
※出典「外れ値とは？Pythonを使用して外れ値の検出方法を実装してみよう」から抜粋。

異常値とは

多くの文献で、外れ値と並んで紹介されるのが、異常値です。外れ値の一種と表現されることもありますが、言葉が持つ意味としては異なります。異常値は外れ値の中で入力ミスや測定ミス等が原因となっているものを指します。つまり、物理的にとりうるはずがない値ということです。例えばものの数を測定するときには、通常は0もしくは正の値しかとりません。その中で負の値を持ったデータがあるなど、とりうるはずのない値が異常値として判定されます。表Aのような倉庫内の製品と在庫数の関係を例にして異常値を確認して見ましょう。

異常値＝外れ値の一種。ただし、外れ値の中で入力ミスや測定ミスが原因となっているものを指す。
物理的にとりうるはずがない値を指す。
正の数しか取りえないものに対して、負の値があるなど。
例をいかに記載します。

※出典「外れ値とは？Pythonを使用して外れ値の検出方法を実装してみよう」から抜粋。

製品「D」が-12個という値だが、在庫数のカウントにおいて値が負の数というのはない。

外れ値が及ぼす影響

例えば以下のようなものがあります。
- 外れ値による統計指標の歪み
- 作業コストの増加
- データ分析の精度の低下

外れ値が及ぼす影響（1次元）

統計指標を歪ませる場合があります。
数値の平均や標準偏差に影響を与える場合がある。

外れ値が及ぼす影響（2次元）

以下は、ある企業での20歳〜40歳までの年齢（歳）と平均年収（万円）の相関が高いと仮定したプロットし、近似直線を描画している。

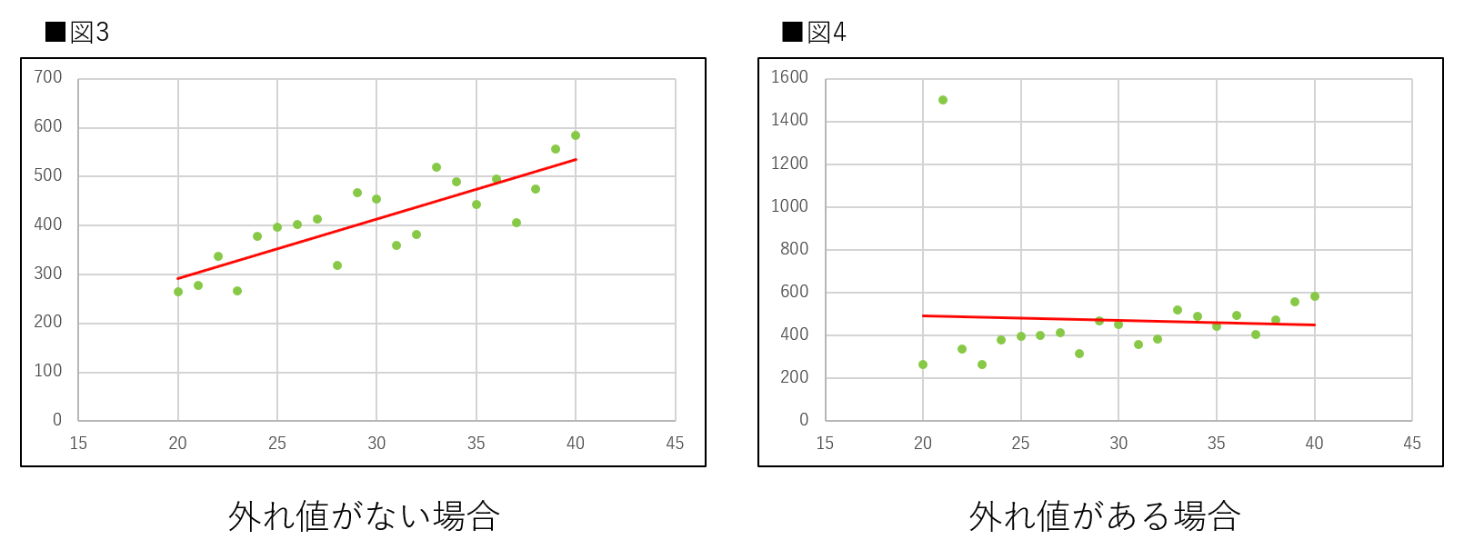
※出典「外れ値とは？Pythonを使用して外れ値の検出方法を実装してみよう」から抜粋。
外れ値がない場合、年齢が上がるにつれて、平均年収もあがる。外れ値の場合は、21歳の平均年収が1500万になっており、その他は、外れ値がない場合と同様。しかし近似的には年齢が上がるにつれて年収が下がるように見える。
外れ値の原因を考える。
- 入力ミス
- 本当に1500万
外れ値の確かな原因が不明なときは、仮説を立ててデータ分析を進めていく。

外れ値の検出方法

検出には様々な手法がある。重要なことはデータセットに合わせた正しい手法の選択と、正しい外れ値を検出できること。

1次元のデータの場合

四分位範囲（IQR）と箱ひげ図

データの広がり具合を示す指標の１つ。
英名を略してIQRとも呼ばれる。
四分位範囲は四分位数を使って求められる。
四分位数は、データの値を小さい順に並べた時にデータを4つに分割する時の区切り値を指す。
小さい順に第1四分位数（Q1）、第2四分位数（Q2）、第3四分位数（Q3）を決める。全て中央値。
四分位範囲は、Q3とQ1の差で求められる。
この四分位範囲を使って外れ値を求める。
- 四分位範囲を1.5倍に拡大し、そこから外れる値を外れ値とする。
- 例）生徒の身長の例

生徒	身長(cm)
G	1.52
J	159
I	162
H	163
F	164
B	165
D	168
C	169
E	177
A	179
平均	150.75

上記の生徒の身長の例を元に四分位を求める。
- Q2は、164.5（165+164 / 2）
- Q1は、162 ---１）とする。
- Q3は、169 ---２）とする。
四分位範囲を計算する。
- ２）−１）→ 169-162 = 7 ---３）とする。
外れ値を計算する
- １） - (1.5 * ３）) → 162 - 1.5 * 7 = 151.5 --- ４）とする。
- ２） + (1.5 * ３）) → 169 + 1.5 * 7 = 179.5 --- ５）とする。
外れ値から外れるものは？
- 各値＜４）→ 151.5より小さいのは、1.52のGになる。
- 各値＞５）→ 179.5より大きいのは、ない。
箱ひげ図は、外れ値を可視化する際に便利な図。四分位半数を含めた数を含めたデータの要約統計量を確認できる。

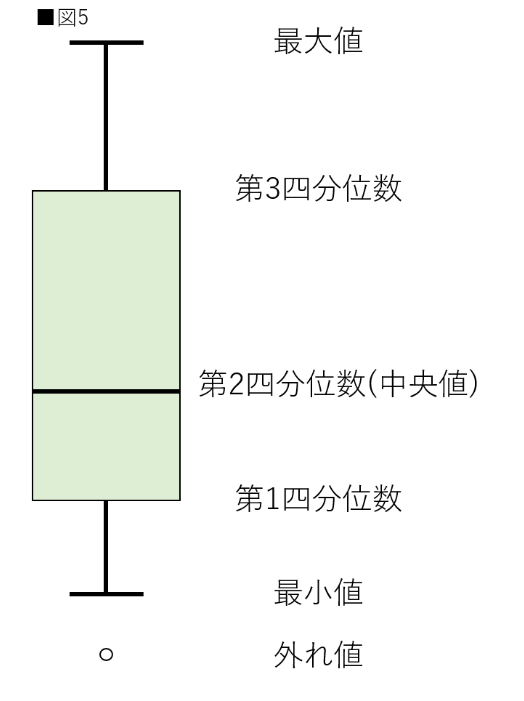
※出典「外れ値とは？Pythonを使用して外れ値の検出方法を実装してみよう」から抜粋。

四分位範囲を用いた外れ値検出は、過程となる確率分布がなく、比較的、汎用性が高いという利点があります。
また、他のデータの箱ひげ図と並べた時にデータのばらつきを簡単に可視化できます。
しかし、データの数が少なかったりすると外れ値の検出がうまくいかない場合もあるため、注意が必要です。

zスコア（z-score）

zスコアは、それぞれのデータの点数を平均点を0、標準偏差を1になるように変換した値のこと。これによりデータは相対的な位置を知ることができる。
zスコアによる外れ値検出は優位水準によって決定される。有意水準が-2と2であれば、外れ値ではないデータは95.45%の中に含まれ、-3と3では99.73%の中に含まれる。
zスコアの公式は、以下の通りです。

$ zn = \frac{x_{n} - \bar{x}}{s} $

$s$は標準偏差
$\bar{x}$ は平均値
$x_n $は各値

生徒	身長(cm)	偏差	偏差の2乗	zスコア
G	1.52	-149.23	22269.5929	-2.978048294
J	159	8.25	68.0625	0.164637797
I	162	11.25	126.5625	0.224506087
H	163	12.25	150.0625	0.244462183
F	164	13.25	175.5625	0.26441828
B	165	14.25	203.0625	0.284374376
D	168	17.25	297.5625	0.344242666
C	169	18.25	333.0625	0.364198763
E	177	26.25	689.0625	0.523847535
A	179	28.25	798.0625	0.563759729
平均	150.752	分散	2511.06554
		標準偏差	50.11

上記の身長の平均を求める。150.75cm
偏差を求める。（各値-平均）
分散を求める。(偏差を2乗して求めた値の平均を求める。）→ 2511.06554
標準偏差を求める。(分散の平方根）→ 50.11
各生徒のzスコアを求める。→上記の通り、Gのスコアは、-2.97となり有意水準が2であれば外れ値として判断されます。

注意点として、zスコアを使用した検定は、データ全体が正規分布に従っていることを仮定としており、
データの形状が正規分布に従わない場合、外れ値検出がうまく行かない場合が存在するとのこと。

トリム平均

トリム平均は、データ全体の最大値と最小値から一定の割当だけ削除し、残ったデータで計算した平均です。
以下に例を示します。

生徒	身長(cm)	削除対象
G	1.52	10%
J	159	20%
I	162
H	163
F	164
B	165
D	168
C	169
E	177	20%
A	179	10%
	10%トリム平均	165.875
	20%トリム平均	165.1666

10%トリム平均の場合、全体の10%を両端から削除し、残った値で平均を求める。→ J〜Eで165.875になる。
20%トリム平均の場合、全体の20%を両端から削除し、残った値で平均を求める。→ I〜Cで165.1666になる。

上記の場合、10%トリムで外れ値1.52が除外されているので、Gの値が152cmだった場合の平均値「165.8」に近づいている事がわかる。

なお、20%トリム平均を使うのは削り過ぎで、実務では稀とのことです。

多次元のデータの場合

機械学習では、基本的には多次元データから予測を立てることが多い。1次元の外れ値検出では検出できない分布がある。
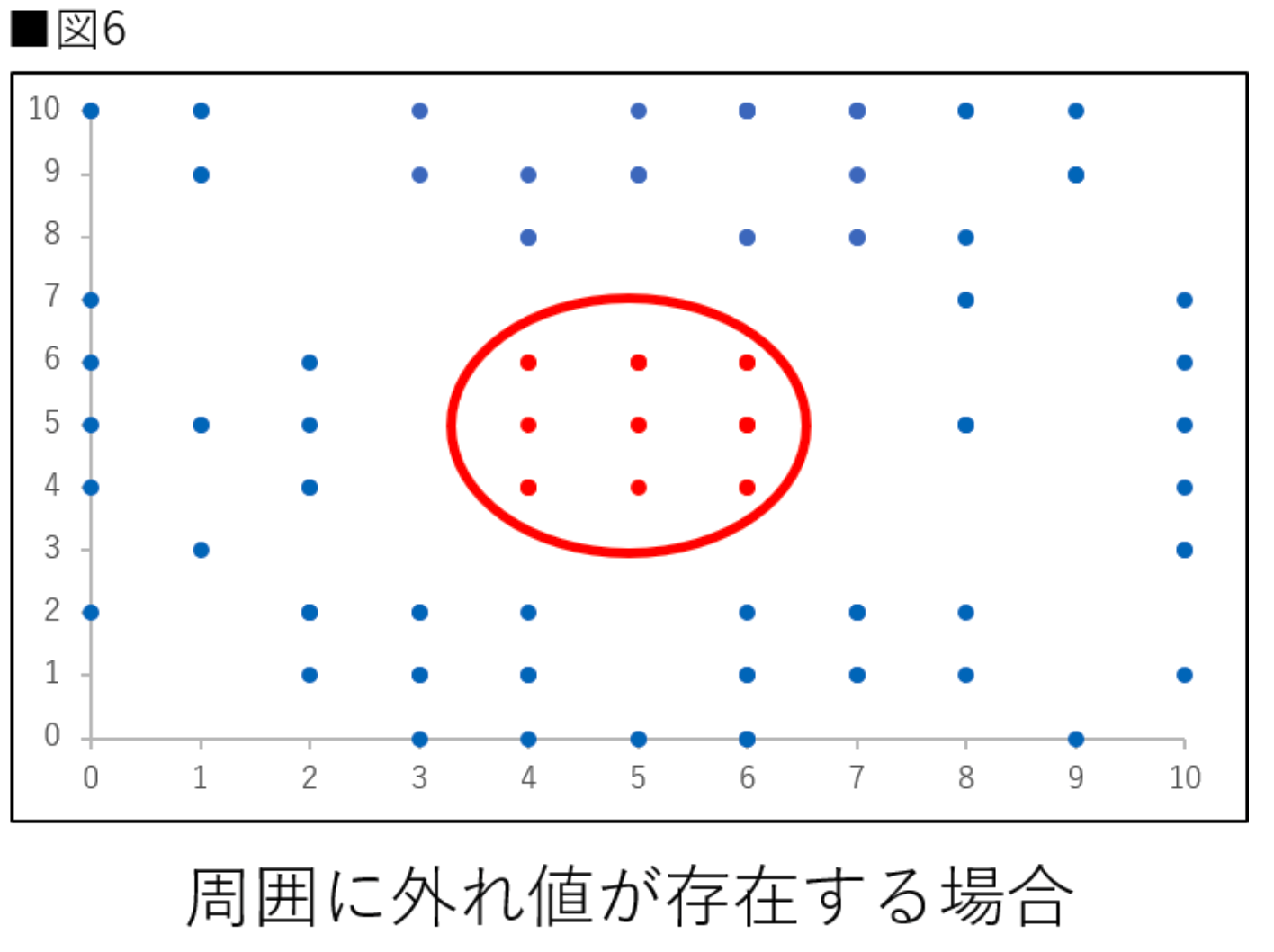
以下に例（分布の真ん中に正しい値を取り、周囲に外れ値が存在してしまっている場合の分布）を示します。

※出典「外れ値とは？Pythonを使用して外れ値の検出方法を実装してみよう」から抜粋。

このような分布の場合、x軸、もしくはy軸単体でデータを確認しても外れ値を検出できなくなっている。
以降で、多次元データの外れ値検出方法を記載する。

Isolation Forest

決定木を用いた外れ値検出。与えられたデータ全体から特徴をランダムに選択し、その特徴の中の最大値と最小値の範囲から分割値を選択し、外れ値が存在していた場合、その部分の決定木の深さは、他のノードの深さに比べて短くなる。

LocalOutlierFactor（LOF）

LOFは値に対する密度を用いた外れ値検出。データ内のそれぞれの点から近くのk個までの値に対する局所密度を求め、比較します。
外れ値が存在していた場合他の点が持つ局所密度よりも、密度が低くなる。

OneClassSVM （OCSVM）

OCSVMはSVMの概念を利用した外れ値検出。OCSVMは外れ値に非常に影響を受けやすく、訓練用データに外れ値が潜んでいた場合、良い結果を得ることができない。正しい値を原点から遠くに、外れ値を原点付近に分布させるような特徴空間に写像させることにより外れ値を検出する。

EllipticEnvelope

データ全体が正規分布に従っていると仮定し、楕円を検出する。正規分布を仮定しているため、従わないデータセットに関しては検出がうまくいかない。

外れ値に対する考え方

異常値であるかを検討する

異常値であるかはしっかりと検討する必要があります。明らかに単位が違っていたり、絶対に取り得るはずのない数値であれば異常値と判断する場合もあるかもしれませんが、実際のデータセットで分析者が独断で異常値と判断するのは慎重にならなければなりません。データ分析者とデータ収集者が別の場合、情報の差し違いなどにより、誤認してしまう可能性があります。「この異常値と思われる値はなぜ発生したのか」という理由まで確認した上で異常値と判断することが必要です。

異常値の可能性があるデータの原因まで確認が必要。

外れ値の除外は慎重に

機械学習を始めたばかりの方の多くは線形回帰やランダムフォレストなどのモデル構築から勉強していく場合が多いです。それは決して悪いことではありません。しかし、モデルの精度を上げることだけを目的とするとデータセット内の邪魔な値（外れ値含む）を極力無くし、汎用的なモデルを作成する方に考えをつぎ込みがちです。kaggleなどのデータ分析コンペティションにおいては単純にスコアを競う場合もあるため、推奨される場合もありますが、現実問題では慎重に考える必要もあります。

実務で外れ地を除外するかは検討が必要。

時に外れ値というのは、それ自体が必要な情報である場合もあります。例えば工場などにおける異常検知などでは、エラー時の値というのが外れ値として記録されたりもします。外れ値（以上検知時の値）を排除して作成した機械学習モデルは通常の作業においては高い精度を出力できるモデルになりますが、異常検知という動作に関しては全くの無意味になる可能性があります。また、上記の図のようにデータ分析者が安易に外れ値を除外することで本来の目的を達成できない可能性もあります。そのため、外れ値への対応は目的と照らし合わせた上でしっかりと検討することが重要です。

向上の機械など異常検知では、エラー時の値が外れ値として記録される場合があるため、外れ値を除外してトレーニングしたモデルが意味のないこともある。目的と照らし合わせて検討すること。

実践

事前準備

ライブラリのインストール

searbornをインストールします。searbornは、Pythonのデータ可視化ライブラリで、同じPythonの可視化ライブラリであるmatplotlibが内部で動いているようです。

pip install seaborn

データを可視化

searbornに用意されているデータセットを使用します。

import numpy as np
import pandas as pd
import copy
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

データセットを確認します。

#アヤメのデータセットの読み込みと表示
df = sns.load_dataset("iris")
print(df.head())
#花の種類を表示
print("花の種類は"+str(df["species"].unique())+"です")

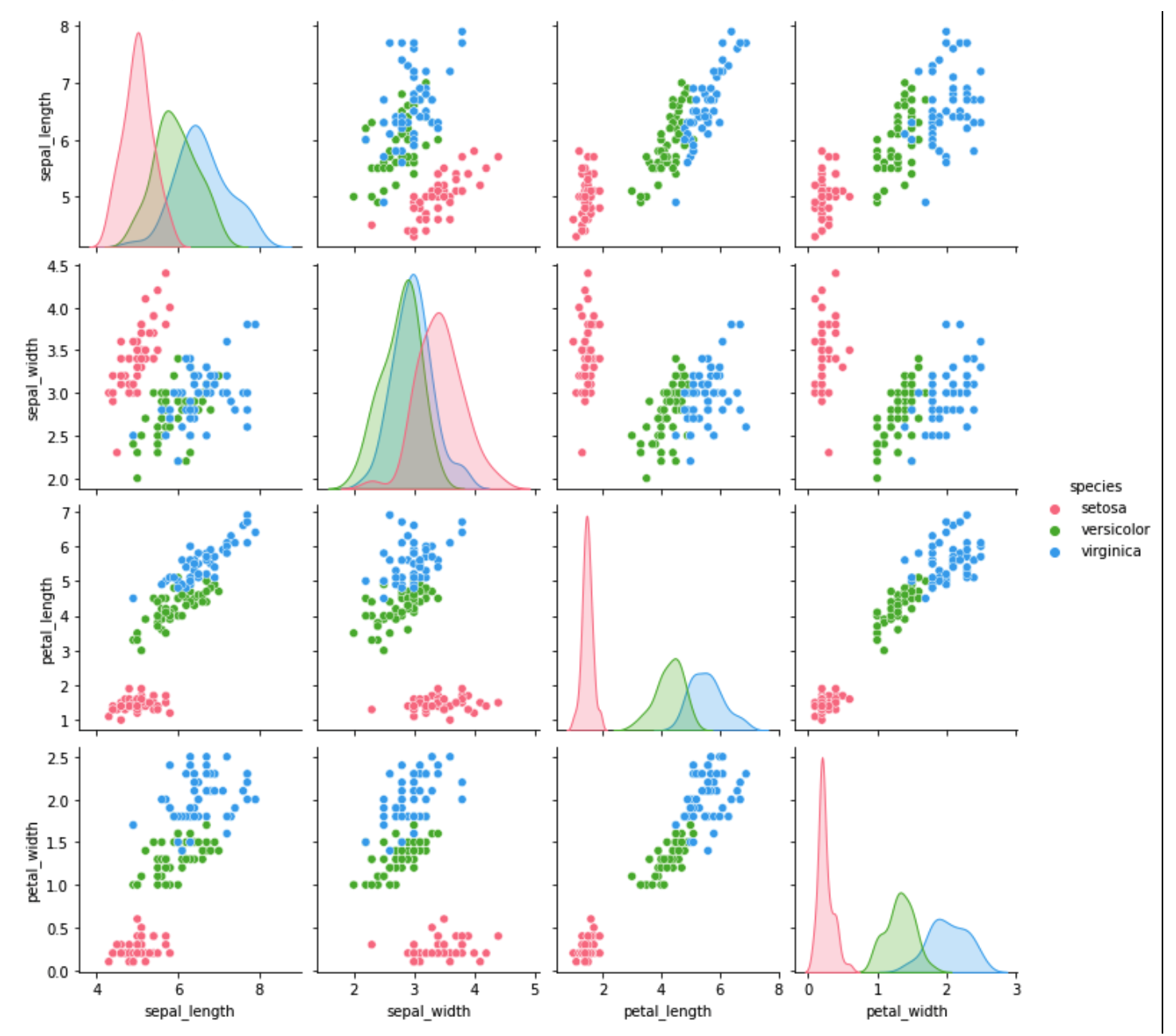
searbornのpairplotを用いて花の種類ごとに色を分けた散布図とヒストグラムを表示します。
特徴量同士の散布図が表示されました。少し外れ値と思われる点を見つけることができると思います。

#花の種類(species)ごとに散布図を表示
sns.pairplot(df, hue='species', palette="husl")

箱ひげ図

データセット全体

アヤメのデータセットの特徴量の中から、それぞれ外れ値を検出します。

箱ひげ図を返す関数を作成.

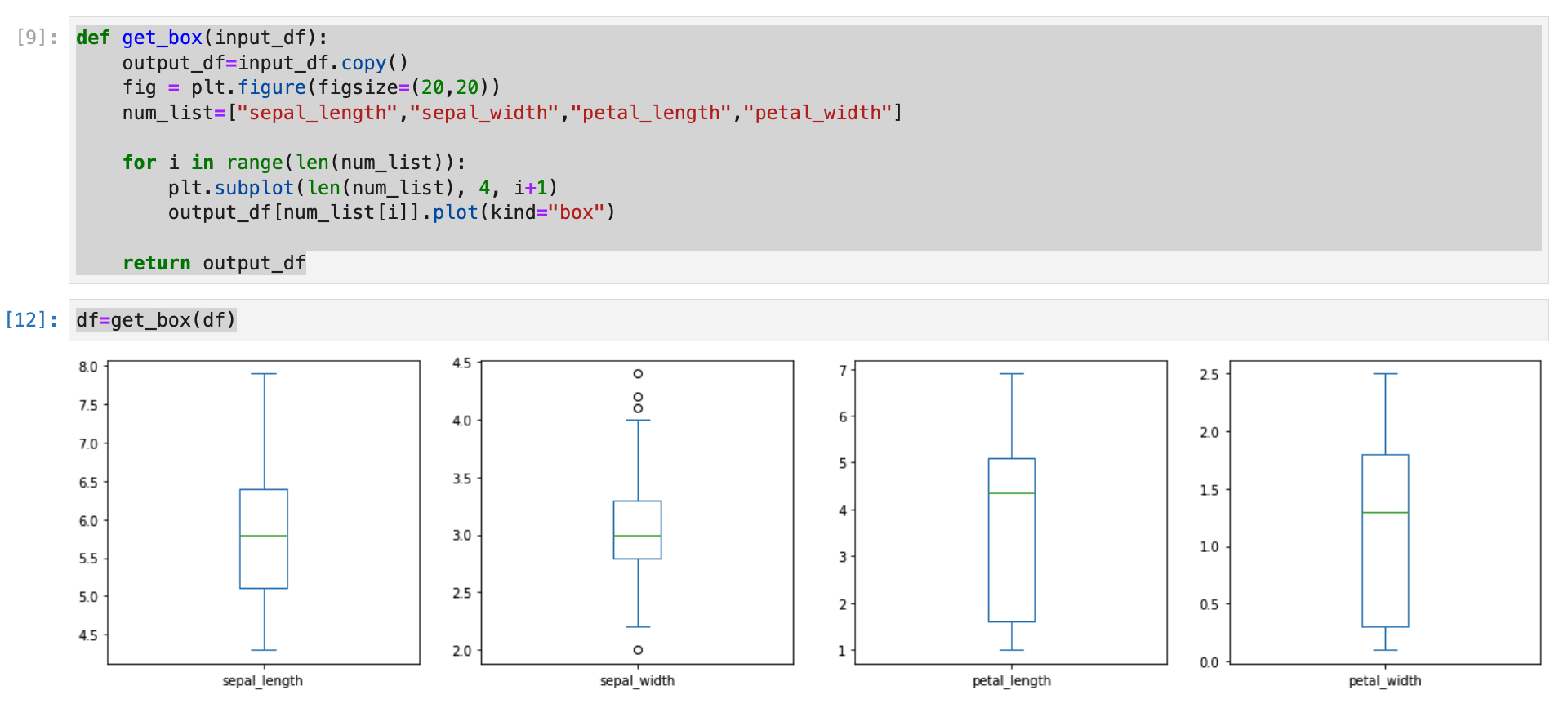
def get_box(input_df):
    output_df=input_df.copy()
    fig = plt.figure(figsize=(20,20))
    num_list=["sepal_length","sepal_width","petal_length","petal_width"]
    
    for i in range(len(num_list)):
        plt.subplot(len(num_list), 4, i+1)
        output_df[num_list[i]].plot(kind="box")
        
    return output_df

呼び出し。

df=get_box(df)

sepal_width（左から2番目）が外れ値を含んでいる。（◯となっている箇所）

詳細な情報を得るためにbox_Outlier()関数を定義する。
この関数では箱ひげ図のそれぞれの四分位数の情報、外れ値の値とindex値を取得します。

def box_Outlier(input_df):
    output_df=input_df.copy()
    num_list=["sepal_length","sepal_width","petal_length","petal_width"]
    for i in range(len(num_list)):
        # 第1四分位
        q1 = output_df[num_list[i]].quantile(0.25)
        # 第2四分位
        q3 = output_df[num_list[i]].quantile(0.75)
        
        #四分位範囲（IQR）を取得
        iqr = q3- q1
        
        # 外れ値基準の下限を取得
        bottom  = q1 - (1.5 * iqr)
        # 外れ値基準の上限を取得
        up = q3 + (1.5 * iqr)
        
        print(str(num_list[i]))
        print("Q1は、"+str(q1))
        print("Q3は、"+str(q3))
        print("IQRは、"+str(iqr))
        print("外れ値は、↓")
        print(output_df[num_list[i]][(output_df[num_list[i]] < bottom) | (output_df[num_list[i]] > up) ])        
        print("*********************")
    return output_df

呼び出し部分。

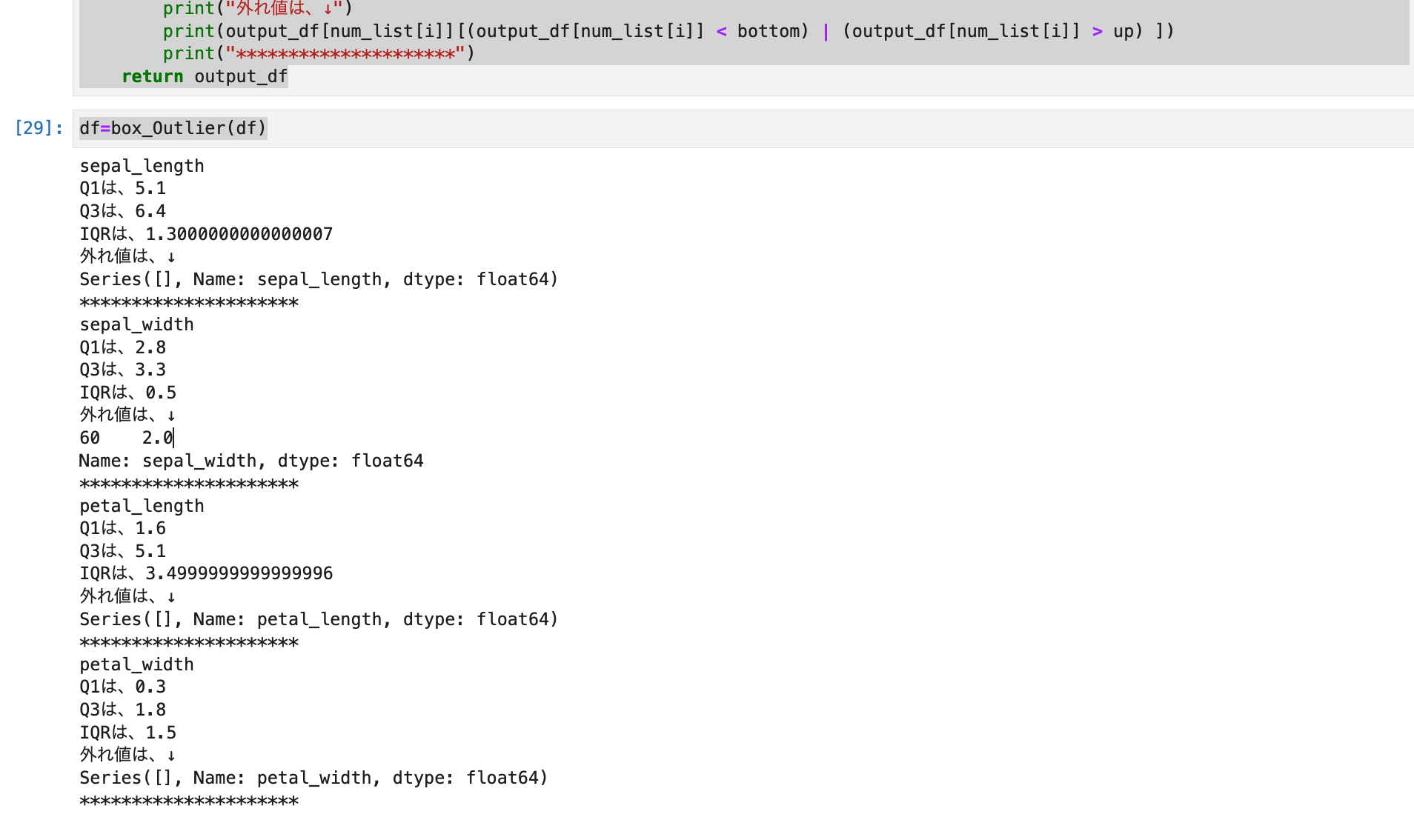
df=box_Outlier(df)

結果は、以下のとおりです。

箱ひげ図で外れ値が確認できたsepal_widthで、上限値を超えた外れ値は以下の通りです。

下限値を超えた外れ値は以下のとおりです。

これにより、外れ値がわかったことで原因を調査し削除もしくは他の値で埋める事が可能です。

上記までは、3種類をまとめた外れ値を検出していました。これでは、データから外れ値を検出することは有効でない可能性があります。
以下に、3種類それぞれに外れ値を検出する例を記載します。

setosa

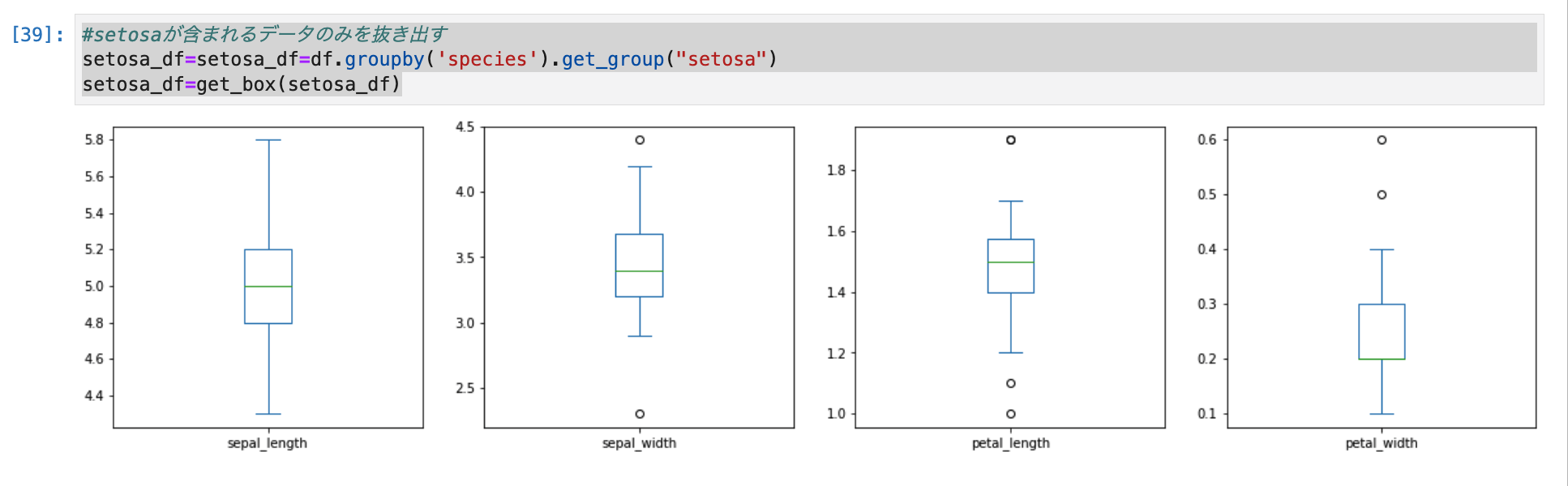
#setosaが含まれるデータのみを抜き出す
setosa_df=setosa_df=df.groupby('species').get_group("setosa")
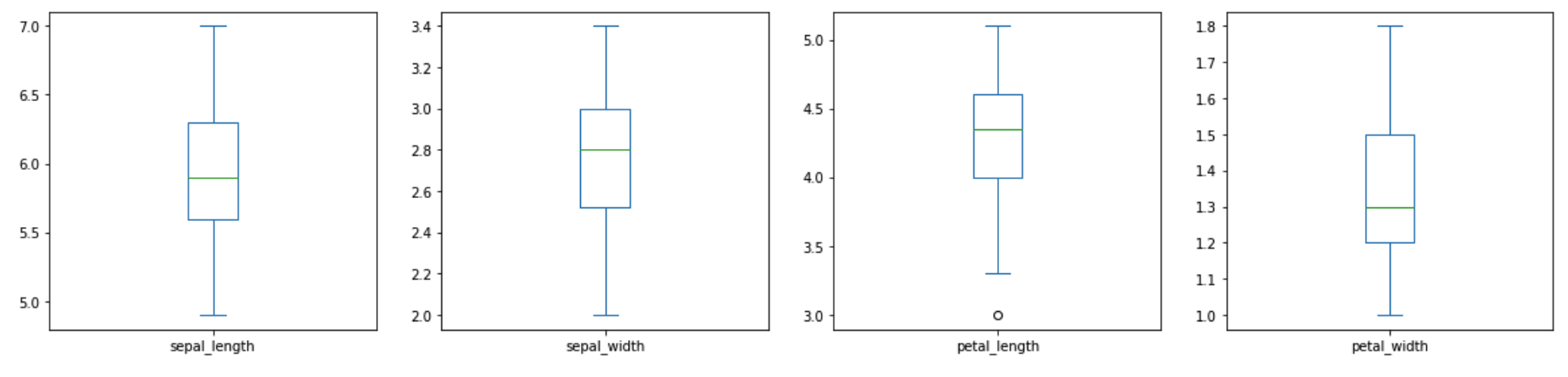
setosa_df=get_box(setosa_df)

setosaに絞り込んだうえで箱ひげ図で確認すると外れ値が確認できました。

詳細を確認します。

setosa_df=box_Outlier(setosa_df)

versicolor

versicolor_df=df.groupby('species').get_group("versicolor")
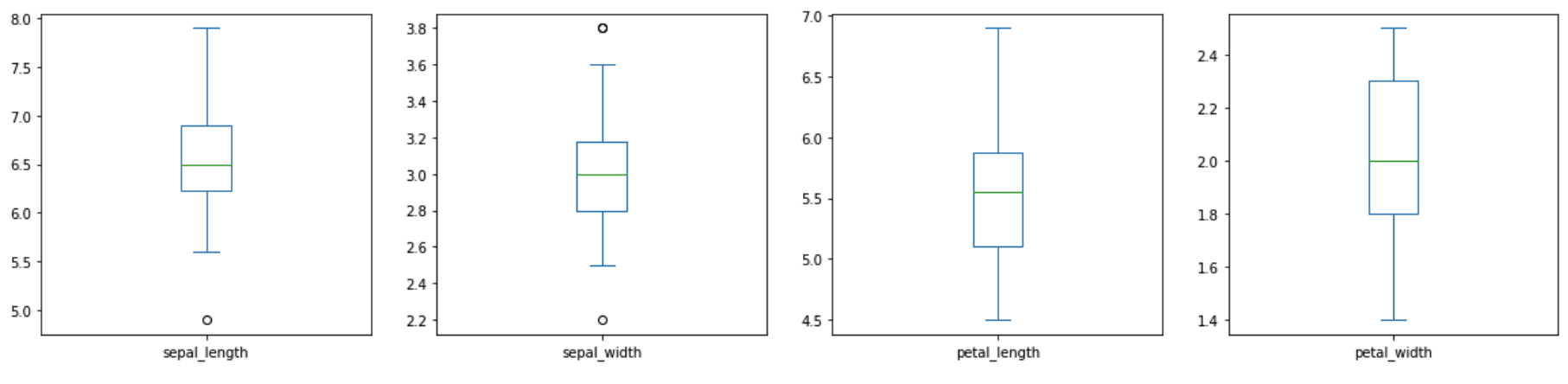
versicolor_df=get_box(versicolor_df)

versicolor_df=box_Outlier(versicolor_df)

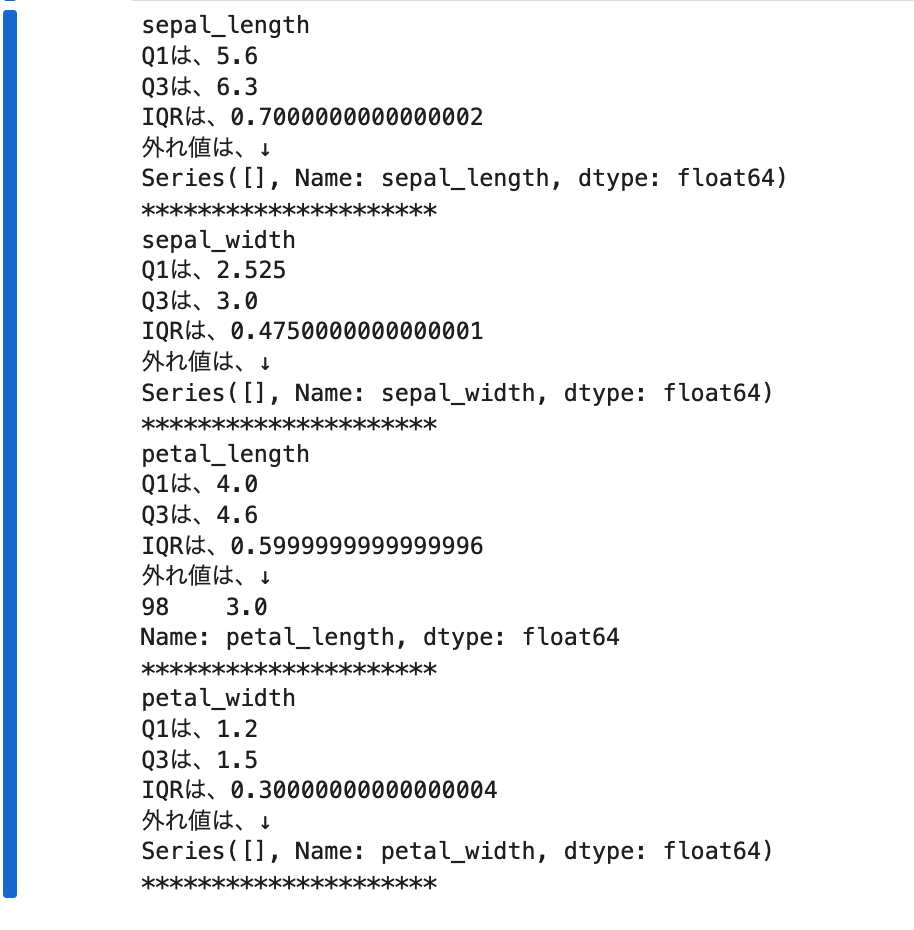
さほど、外れ値はない。

virginica

virginica_df=df.groupby('species').get_group("virginica")
virginica_df=get_box(virginica_df)

virginica_df=box_Outlier(virginica_df)

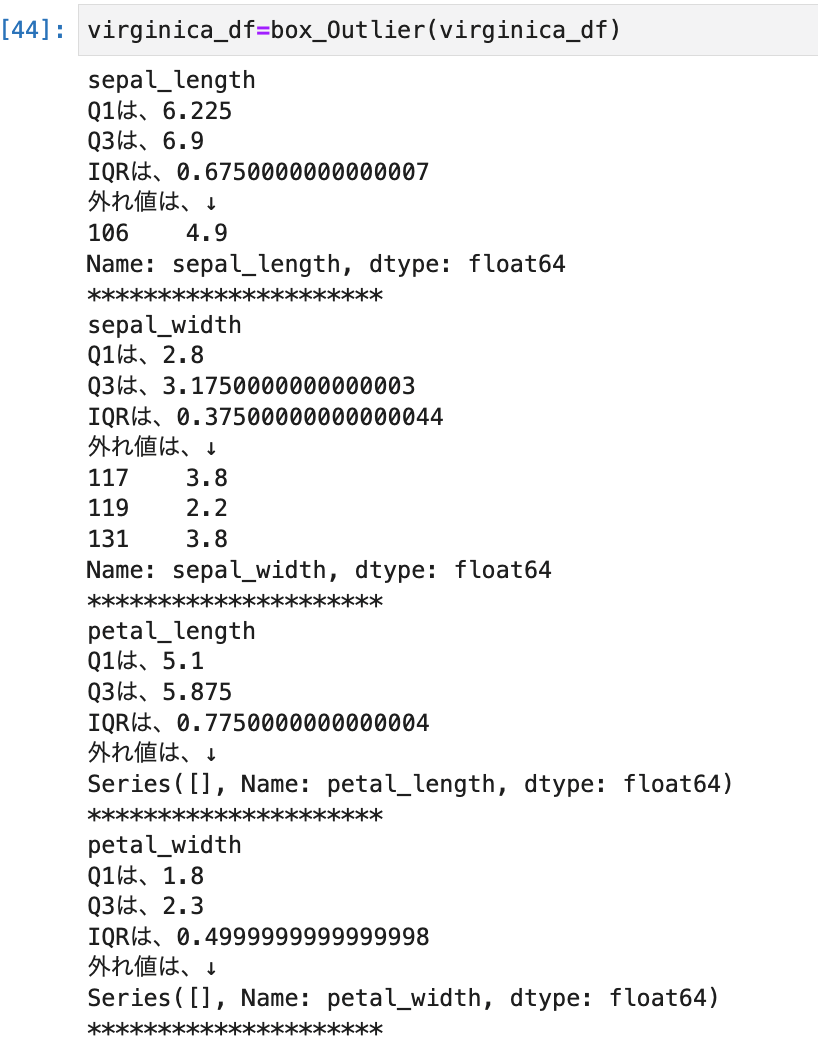
zスコア

アヤメの種類ごとにデータをヒストグラムで表示します。

ヒストグラム

関数を作成します。

def get_hist(input_df):
  output_df=input_df.copy()
  fig = plt.figure(figsize=(20,20))
  num_list=["sepal_length","sepal_width","petal_length","petal_width"]

  for i in range(len(num_list)):
    plt.subplot(len(num_list), 4, i+1)
    output_df[num_list[i]].plot.hist(bins=15)
  return output_df

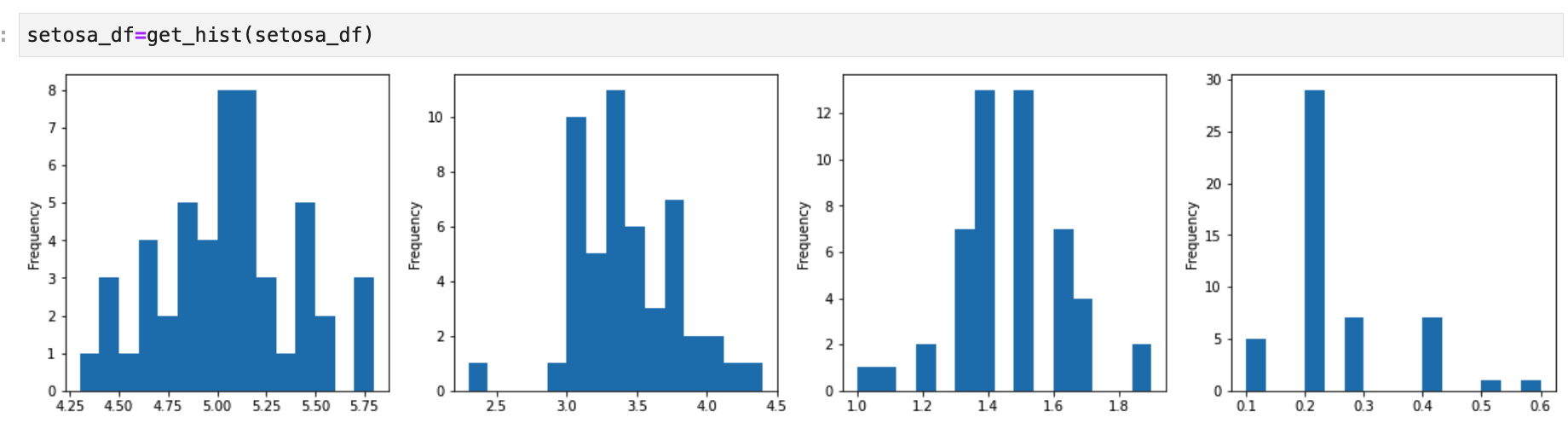
setosa_df=get_hist(setosa_df)

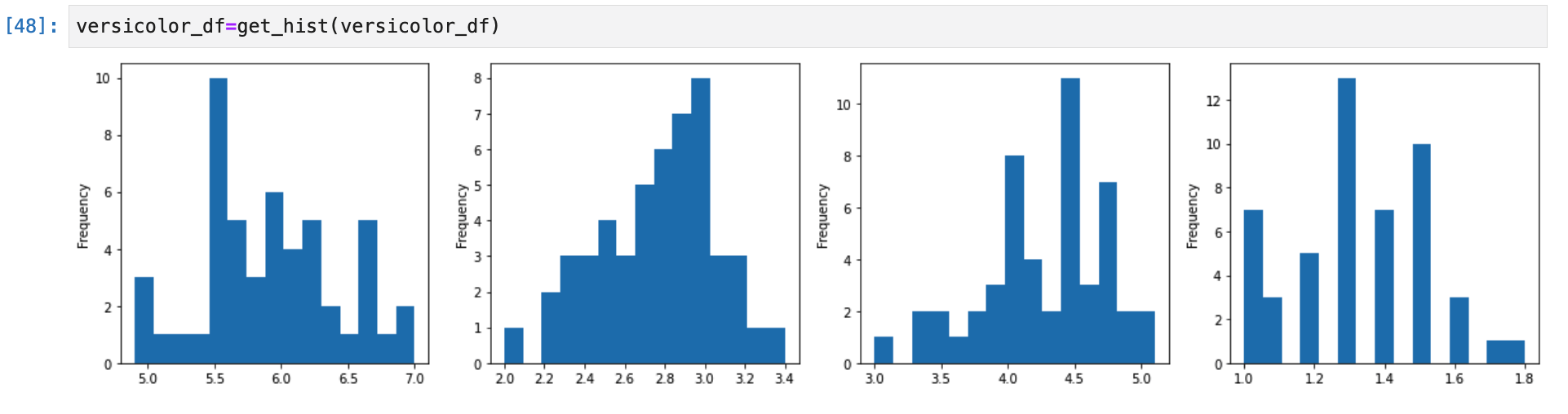
versicolor_df=get_hist(versicolor_df)

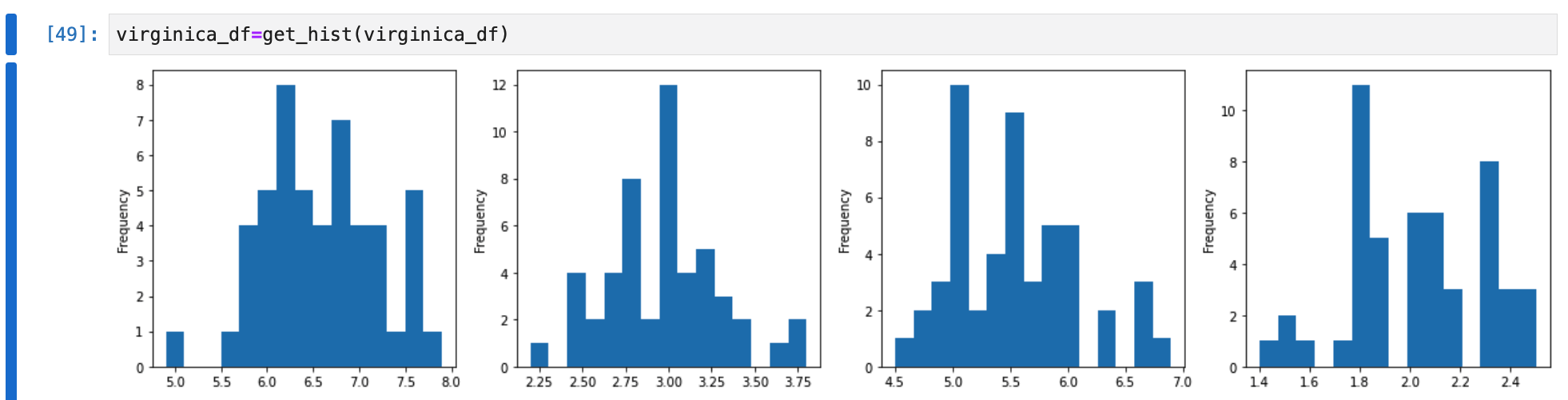
virginica_df=get_hist(virginica_df)

詳細

優位水準を2にします。

def get_zscore(input_df):
  output_df=input_df.copy()
  num_list=["sepal_length","sepal_width","petal_length","petal_width"]

  for i in range(len(num_list)):
    #列の平均を求める
    mean=output_df[num_list[i]].mean()
    #列の標準偏差を求める
    std=output_df[num_list[i]].std(ddof=0)
    #zスコアを求める
    zscore=(output_df[num_list[i]]-mean)/std
    #列名、平均、標準偏差、外れ値を表示
    print(str(num_list[i]))
    print("平均は："+str(mean))
    print("標準偏差は："+str(std))
    print("外れ値は↓")
    print(str(output_df[num_list[i]][(zscore<-2)|(zscore>2)]))
    print("*********************")
  return output_df

setosa

setosa_df=get_zscore(setosa_df)

versicolor_df

versicolor_df=get_zscore(versicolor_df)

versicolor

virginica_df=get_zscore(virginica_df)

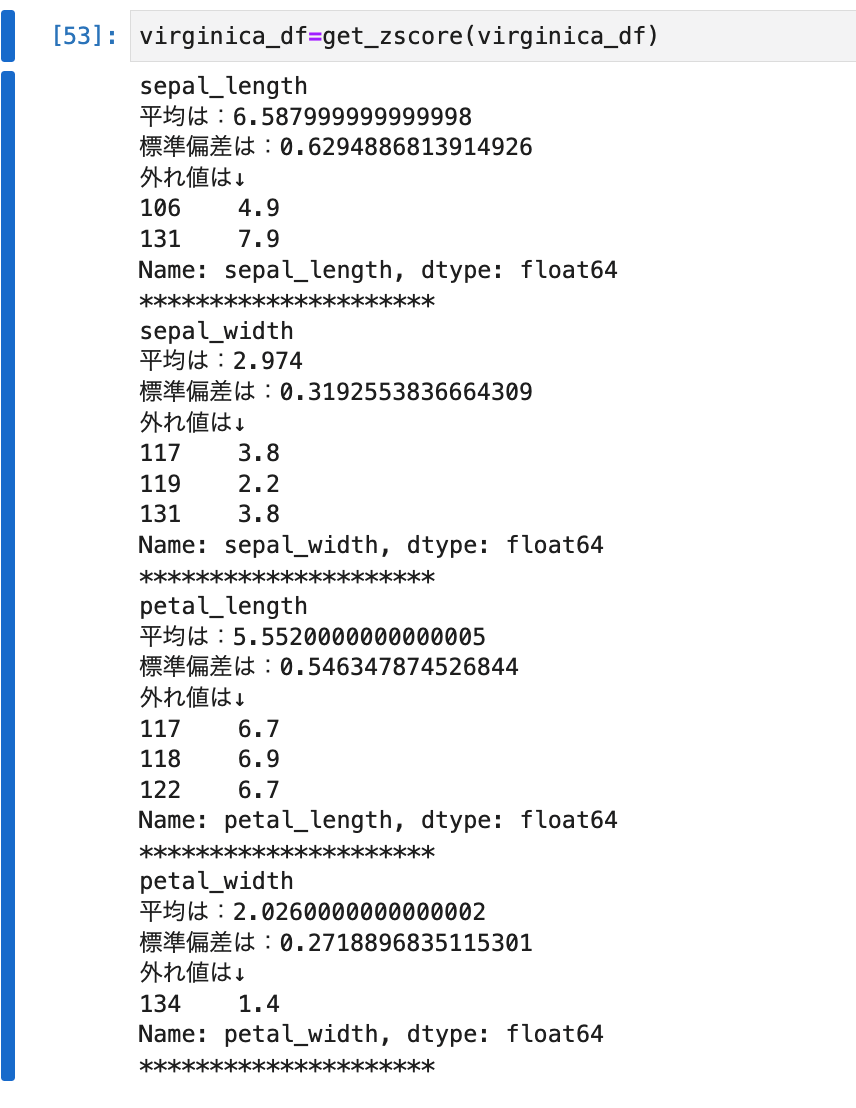
考察

今回は、zスコアと四分位範囲の検出方法を実装しました。他にも検出方法が複数あるので今後試してみたいと思います。

【初心者】特徴量エンジニアリング（外れ値）について調べてみた

背景・目的

まとめ

概要

外れ値とは

異常値とは

外れ値が及ぼす影響

外れ値が及ぼす影響（1次元）

外れ値が及ぼす影響（2次元）

外れ値の検出方法

1次元のデータの場合

四分位範囲（IQR）と箱ひげ図

zスコア（z-score）

トリム平均

多次元のデータの場合

Isolation Forest

LocalOutlierFactor（LOF）

OneClassSVM （OCSVM）

EllipticEnvelope

外れ値に対する考え方

異常値であるかを検討する

外れ値の除外は慎重に

実践

事前準備

ライブラリのインストール

データを可視化

箱ひげ図

データセット全体

setosa

versicolor

virginica

zスコア

ヒストグラム

詳細

setosa

versicolor_df

versicolor

考察

参考