LoginSignup
4
3

More than 1 year has passed since last update.

@zumax

【初心者】データのスケーリングを調べてみた

Last updated at Posted at 2022-05-01

背景・目的

私は、現在データエンジニアリングを生業としています。普段は、データ基盤の構築やパフォーマンスチューニングなどに従事しています。
ビックデータの収集や、蓄積、分析などの環境構築の経験はそこそこありますが、機械学習による予測や分類などのスキルは持ち合わせていませんでした。
今まで機械学習を避け続けてきましたが、一念発起し学ぼうと思います。

学び方としては、AWS Certified Machine Learning – Specialty（以降、ML試験という。）の勉強を通して、理解を深めていこうと思います。
ML試験のガイドを読むと、第２分野に探索的データ解析が出ていましたので、そこから学びたいと思います。

前回は探索的データ解析により、データの特徴を掴むための手法を学びましたが、今回は、スケーリングについて学びたいと思います。

まとめ

  • 機械学習では、データが必要であり、そのデータに外れ値が混ざっていると予測の精度が下がります。
  • また、各データの値は重みを平等にすることが重要で、そのためには前処理でスケーリング（正規化、標準化）を行うことが必要になります。

概要

前回同様に、codexaさんの記事「正規化・標準化を徹底解説 （Python 前処理 サンプルコード付き）」を元に学んでいきたいと思います。

機械学習の力を最大限活かすためには前処理が重要とのこと。
今回は、機械学習の前処理の「正規化」と「標準化」を理解します。

スケーリングとは？

  • Feature Scaling
  • 特徴量において値を一定のルールに基づいて一定の範囲に変換する処理のことを指します。
  • スケーリングには、以下が含まれます。
    • 正規化
      • 0〜1に変換します。
    • 標準化
      • 平均を0、分散を1に変換します。
  • スケーリングは、全ての機械学習モデルに有効に働くわけではない。

スケーリングの目的①

  • 特徴量が持つ値の持つ重みを平等にすること。
  • 特徴量間の距離をベースにした以下のようなモデルに有効とのことです。
    • SVN（Support Vector Machine）
    • kNN(k-Nearest Neighbors)
  • 機械学習で扱う特徴量には、基本的に数値が扱われる。そのため数値同士を同じ尺度で扱ってしまう可能性があるとのことです。
    • 詳細は、codexaさんのページをご確認いただくとして、例えばA〜Eの生徒がいたとき身長と平熱の特徴量があるときに、ユーグリッド距離を用いて、生徒同士の距離を測った場合、平熱の幅よりも身長の幅が広くなってしまいました。（身長の重みが大きくなっていました。）
    • 本来単位が違うはずの特徴量を同じ尺度で捉えようとすると、比較が難しい場合がある例でした。
  • 上記の特徴量で、標準化のスケーリングを適応した場合、ユーグリッド距離の差が小さくなりました。
    • 繰り返しですが標準化は、各特徴量の平均を0、標準偏差が1になるような分布に変換している。

スケーリングの目的②

  • 学習コストの削減も目的の一つです。
  • 以下のモデルで有効とされているようです。
    • 線形回帰
    • ニューラルネットワーク
  • 特徴量の範囲が異なることで、再急降下時に更新されるパラメータのサイズが異なってしまうようです。学習がスムーズに行われるためにはスケーリングが必要とのことでした。
    • 最急降下法について、私は理解できていないので後ほど学習したいと思います。

スケーリングの影響が少ないモデル

  • 比較的影響を受けにくいモデルとして、以下のようなツリーベース型のものあるようです。
  • ツリーベース型のモデルは各特徴量内の分割を繰り返すため、特徴量同士のスケールを合わせなくても、影響を受けにくいようです。

正規化と標準化の定義と実装

正規化とは？

  • Normalizationと呼ぶ。
  • Normalizationは、複数の手法を持っているが、ここでは、min-max normalizationとする。
  • 正規化についての数式は、以下の通り。

$ \large{ x_{norm}^i = \frac{x^i-x_{min}} {x_{max} - x_{min}} } $

  • $ x^i　\quad $ 特徴量内の各値

  • $ x_{min} \quad $ 特徴量内の最小値

  • $ x_{max} \quad $ 特徴量内の最大値

  • 特徴量の各値を最小値から引いたもの（上記の分子）を、特徴量内の最大値から最小値を引いた値（上記の分母）で割ることで正規化を行っています。

使用する際の注意点

  • 正規化は外れ値に敏感であることらしいです。
  • 非常に大きな値や小さな値が外れ値として存在していた場合、他の値が0や1に引っ張られる。（確かに式を見るとそれはありそう）
  • そのため、正規化を使用する場合は、外れ値が存在しないか確認する必要があります。

外れ値の有無の違いを確認してみる

外れ値なしの場合

■表A

生徒 身長(cm) 平熱(℃)
A 168 37.1
B 170 36.3
C 168 35.6
D 162 36.1
E 182 36.1

↓

■表C（正規化後）

生徒 身長(cm) 平熱(℃)
A 0.3 1
B 0.4 0.466667
C 0.3 0
D 0 0.333333
E 1 0.333333
  • $ \large{x_{min}} \quad$ 身長は、162cm、平熱は、35.6℃
  • $ \large{x_{max}} \quad$ 身長は、182cm、平熱は、37.1℃
  • $ \large{x_{max}-x_{min}} \quad$ 身長は、20、平熱は、1.5
外れ値ありの場合

■表D

生徒 身長(cm) 平熱(℃)
A 168 37.1
B 170 36.3
C $ \color{red}{10000} $ 35.6
D 162 $ \color{red}{0} $
E 182 36.1

↓

■表E（正規化後）

生徒 身長(cm) 平熱(℃)
A 0.000061 1
B 0.000813 0.959569
C 1 0.959569
D 0 0
E 0.002033 0.973046
  • $ \large{x_{min}} \quad$ 身長は、162cm、平熱は、0℃
  • $ \large{x_{max}} \quad$ 身長は、100000cm、平熱は、37.1℃
  • $ \large{x_{max}-x_{min}} \quad$ 身長は、9838、平熱は、37.1

外れ値の注意点

  • 表Dでは、生徒Cの身長が10000cm、生徒Dの平熱が0℃になっておりこれが外れ値である。
  • そのため、身長は0付近、平熱は1付近に値が引っ張られている。

標準化とは？

  • Standardization

  • 基本的には、平均を0、標準偏差を1とする変換として定義されているとのこと。

  • 入力の特徴量が正規分布に従う仮定した変換を行うことができます。

  • 式は、以下のとおりです。
    $ \large{ x_{std}^i = \frac{x^i - μ} {σ} } $

  • $ x^i　\quad $ 特徴量内の各値

  • $ μ \quad $ 特徴量内の平均値

  • $ σ \quad $ 特徴量内の標準偏差

  • 特徴量内の各値から平均値を引いた値を、標準偏差で割ることで、標準化を実現します。

  • 標準化は、分布内の平均値を0、標準偏差を1にする変換とのことです。

  • （正規化が0〜1の範囲に収めているのとは異なり、標準化は特定の範囲に収めるような変換ではない）

  • 標準偏差（σ）には以下のものがあります。

    • 通常の標準偏差
    • 不偏標準偏差

  • データには以下のものがあります。

    • 母集団と呼ばれる全体を示すデータ
    • 標本と呼ばれる母集団から抽出されたデータ

  • 分散には以下のものがあります。

    • 母集団から求められる分散を母分散
    • 標本から求められる分散を不偏分散

  • 統計学的に、不偏分散は母分散よりも少しだけ小さくなることが知られているとのこと。分散の平方根である標準偏差にも若干の違いが生まれるらしいです。

正規化と標準化のどちらを使用するべきか

  • 使用するモデルや精度と比較しながら検討することであり、一概に決めることはできないとのこと。
  • 例えば正規化は外れ値に敏感でありますが、外れ値が存在するというだけで使用しないわけではないようです。
  • 外れ値を除外して正規化を用いる場合もあるようです。
  • こういった判断は知識と経験の積み重ねで実現され、与えられた課題に対して今までの経験や知識から、どちらを使用するべきか判断するという場合が多いようです。

実践

正規化のPython実装

準備(乱数の生成)

  • 正規化を行うため、準備として乱数を生成します。
# NumpyとMatplotlib、Pandasのインポート
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# シードを用いることで発生する乱数の固定が可能
np.random.seed(seed = 0)

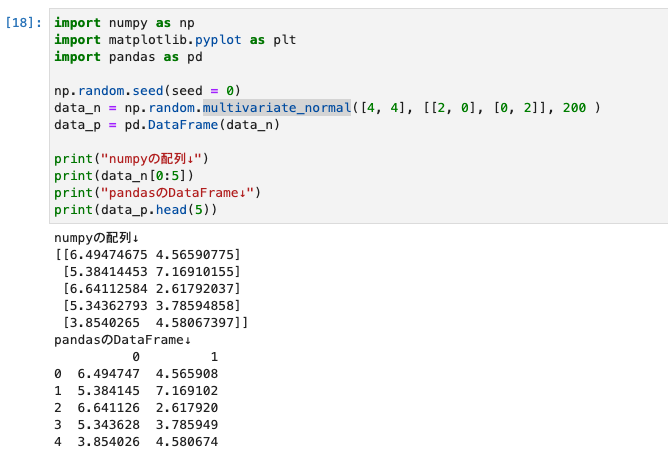
data_n = np.random.multivariate_normal([4, 4], [[2, 0], [0, 2]], 200 )
data_p = pd.DataFrame(data_n)

print("numpyの配列↓")
print(data_n[0:5])
print("pandasのDataFrame↓")
print(data_p.head(5))
  • 結果は、以下のとおりです。

image.png

sklearnのインストール

  • 次のステップで必要になるため事前にインストールしておきます。
pip install sklearn

1.scikit-learnによる正規化の実装（正規化前後のプロットを含む）

  • スケーリング前とスケーリング後の点を可視化するための関数を定義します。
def image_show(data_before,data_after,title):
    # 出力サイズ
    plt.figure(figsize=(8,8))
    # タイトル
    plt.title(title)
    
    # X軸とY軸の範囲を定義
    plt.xlim([-8,8])
    plt.ylim([-8,8])
    
    # 目盛りの刻み
    plt.xticks(np.arange(-8,9,1))
    plt.yticks(np.arange(-8,9,1))
    
    # プロットの設定
    plt.scatter(data_before[:,0],data_before[:,1],c='blue',s=10,label='before')
    plt.scatter(data_after[:,0],data_after[:,1],c='red',s=10,label='before')
    
    # ラベルの設定
    plt.legend(fontsize = 15)
    
    # 中心ラインの設定
    plt.hlines(0, xmin = -8, xmax = 8 , linestyles='dashed')
    plt.vlines(0, ymin = -8, ymax = 8 , linestyles='dashed')
    
    plt.show()
    return
  • scikit-learnのMinMaxScalarクラスを用いて実装します。
from sklearn.preprocessing import MinMaxScaler
#正規化のクラスを準備
ms = MinMaxScaler()
#特徴量の最大値と最小値を計算し変換
data_sc = ms.fit_transform(data_n)
#プロット
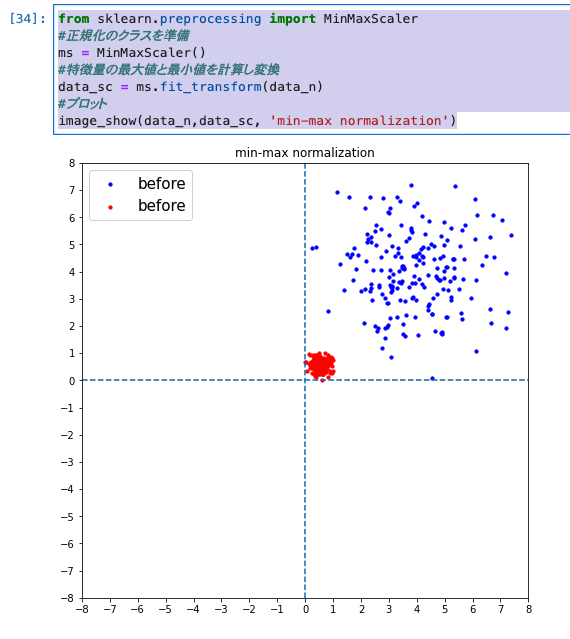
image_show(data_n,data_sc, 'min-max normalization')
  • 実行結果は、以下のとおりです。

image.png

  • 正規化後がimage_show関数のdata_afterに入り、赤字で表示されています。

  • 確かに0〜1の間に値が値が集まっているようです。

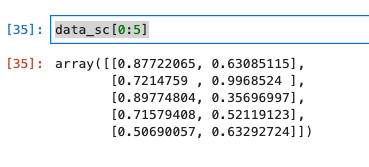
  • 正規化後の値を確認してみます。

data_sc[0:5]

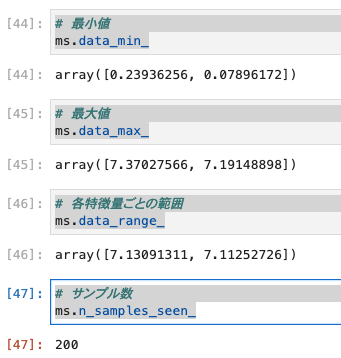
image.png

  • 各特徴量の統計値を確認します。
# 最小値
ms.data_min_

# 最大値
ms.data_max_

# 各特徴量ごとの範囲
ms.data_range_

# サンプル数
ms.n_samples_seen_
  • 実行結果は、以下のとおりです。
    image.png

2.Numpyによる正規化の実装

  • Numpyのメソッドを用いて実装を行います。乱数については、最初に定義したdata_n変数を用います。
  • Numpyのメソッドを用いた場合は、scikit-learnとは異なり、正規化の計算式を定義してあゲル必要があります。
  • min_max_n()という関数を作成し、正規化後の値を返すようにします。
def min_max_n(n, axis=None):
    # 最小値の計算
    min_n = n.min(axis= axis, keepdims = True)
    # 最大値の計算
    max_n = n.max(axis=axis, keepdims = True)
    
    # 正規化の計算 ※ 数式で書いたものと同じ！
    min_max_n = (n - min_n) / (max_n - min_n)
    
    return min_max_n
  • 実行
print("正規化前")
print(data_n[0:5])
print("正規化後")
print(min_max_n(data_n,axis=0)[0:5])
  • 実行結果は、以下のとおりです。

image.png

  • 1.scikit-learnによる正規化の実装と同じ値が出力されています。実装量で言えばscikit-learnを用いたほうが簡単。
  • ここでは、実装の内容を知る意味で実装をしているとのこと。

3.Pandasによる正規化の実装

  • DataFrame型であったとしてもscikit-learnを用いて正規化は実装可能.
  • Pandasを用いて実装することで、内容を理解する。
  • min_max_pという関数を作成します。
def min_max_p(p):
    min_p = p.min()
    max_p = p.max()
    min_max_p = (p - min_p) / (max_p - min_p)
    return min_max_p
  • 1.scikit-learnによる正規化の実装、2.Numpyによる正規化の実装と同じ値が出力されていることを確認できました。

標準化のPython 実装

  • 乱数に関しては正規化で作成したものを使用します。
  • 使用するライブラリによって、標準偏差のみ使用できるものと、不偏標準偏差も使用できるものがあるようです。そのため以下の実装を確認します。
    • 1.scikit-learnによる標準化の実装については、標準偏差のみ
    • 2.Numpyによる標準化の実装と、3.Pandasによる標準化の実装では、標準偏差と不偏標準偏差の両方

1.sckit-learnによる標準化の実装（標準化前後のプロットを含む）

  • プロットする関数には、既に作成したimage_showを利用します。
from sklearn.preprocessing import StandardScaler
# 標準化のクラスを定義
ms = StandardScaler()
# 特徴量の平均値と標準化を計算し、特徴量のスケール変換を行ってくれます。
data_std = ms.fit_transform(data_n)

image_show(data_n,data_std,'Standardization')
  • 実行結果は、以下のとおりです。
  • 値を確認します。
# 標準化前
print("標準化前")
print(data_n[0:5])

# 標準化後
print("標準化後")
print(data_std[0:5])
  • 値やプロットした結果を確認すると、0付近に分布していることが分かりました。
# 各特徴量ごとの平均値
print(ms.mean_)
# 各特徴量ごとの標準偏差
print(ms.var_)
# サンプル数
print(ms.n_samples_seen_)
  • 結果は、以下のとおりです。

2.Numpyによる標準化の実装

  • Numpyで標準式の計算式を定義する関数を作成します。
    • standard_n()という関数を作成し正規化後の値を返すようにします。
def standard_n(n, axis=None, ddof=0):
    # 平均値を計算
    mean_n = n.mean(axis = axis , keepdims = True)
    # 標準偏差を計算。ddofが0ならば標準偏差、ddofが1ならば不標準偏差
    # keepdims:配列の次元数を落とさずに結果を求めるための引数
    std_n = n.std(axis = axis , keepdims = True, ddof = ddof)
    # 標準化の計算
    standard_n = (n - mean_n) / std_n
    
    return standard_n

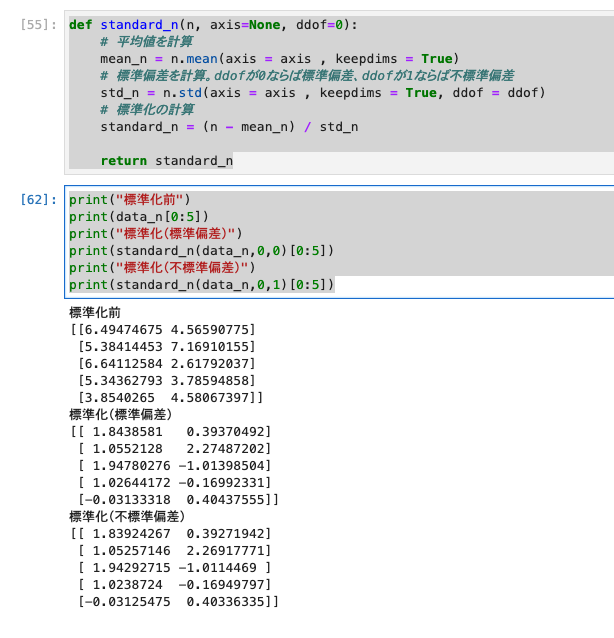
print("標準化前")
print(data_n[0:5])
print("標準化（標準偏差）")
print(standard_n(data_n,0,0)[0:5])
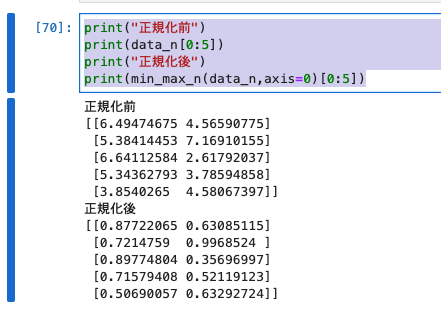
print("標準化（不標準偏差）")
print(standard_n(data_n,0,1)[0:5])
  • 実行結果は、以下のとおりです。

image.png

3.Pandasによる標準化の実装

  • 正規化後の値を返すstandard_pという関数を作成します。
def standard_p(p, ddof=1):
    # 平均値
    mean_p = p.mean()
    # 標準偏差
    std_p = p.std(ddof = ddof)
    # 標準化の計算
    return (p - mean_p) / std_p

print("標準化前")
print(data_p[0:5])
print("標準化(標準偏差)")
print(standard_p(data_p,ddof=0).head(5))
print("標準化(不偏標準偏差)")
print(standard_p(data_p,ddof=1).head(5))
  • 実行結果は、以下のとおりです。

正規化・標準化を用いたワインの分類

  • scikit-learnを用いて利用できるワイン認識のデータセットを用いて機械学習における分類問題を実装します。
  • 主に正規化と標準化を適応する場合と適応しない場合の比較を中心に確認を行います。

事前準備

  • 上記で既に実装像済みですが、あらためてimportの実装を行います。
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
  • ワインのデータを読み込みます。
  • sklearnには、データセットが予め定義されているようです。
from sklearn.datasets import load_wine
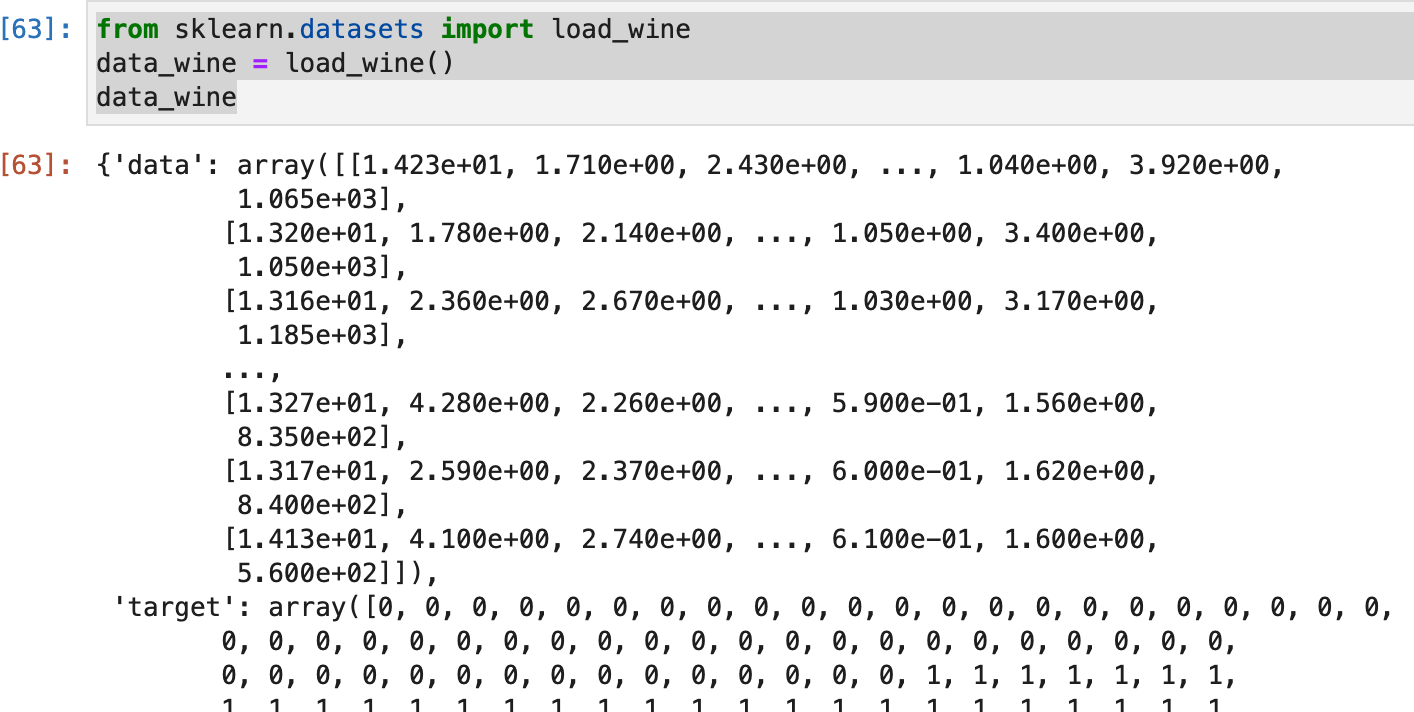
data_wine = load_wine()
data_wine
  • 結果は、以下のとおりです。（下の方は、省略しています。）
  • Pandasを用いて予測に必要なラベルを抽出します。
df_wine = pd.DataFrame(data_wine['target'],columns=['wine'])
df_wine.head(5)
  • 結果は、以下のとおりです。
  • 各特徴量も、ラベルと同様にDataFrame型で抽出します。
df_data = pd.DataFrame(data_wine['data'],columns=data_wine['feature_names'])
df_data.head(5)
  • 結果は、以下のとおりです。

image.png

  • 各特徴量の値が表示されました。
  • このワインのデータセットには、訓練データと、検証用データに分かれていないので2分割します。
    • 半分を訓練用、半分を検証用に分割します。
    • ワインのラベルの割合を等しくするために、 stratify引数でラベルを指定します。
from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y = train_test_split(df_data,df_wine,test_size=0.5,stratify=df_wine['wine'],random_state=0)
  • 特徴量と各ラベルに分割できました。
  • 正規化と標準化の実装を行います。
from sklearn.preprocessing import StandardScaler,MinMaxScaler
mmsc = MinMaxScaler()
stdsc = StandardScaler()
  • 別々にfit()やfit_transform()メソッドを用いると、正規化や標準化の計算条件が異なってしまう可能性があるため、訓練データと検証データに適用するクラスは同じものを使用すること。
  • 訓練用データでfit()やfit_transform()メソッドを用いて正規化や標準化のパラメータを計算し、検証用データにはtransform()メソッドを用いてスケーリングを行います。
#注意
#→訓練データでfitした変換器を用いて検証データを変換すること
#訓練用のデータを正規化
train_mm = mmsc.fit_transform(train_x)
#訓練用のデータを標準化
train_std = stdsc.fit_transform(train_x)
#訓練用データを基にテストデータを正規化
test_mm=mmsc.transform(test_x)
#訓練用データを基にテストデータを標準化
test_std = stdsc.transform(test_x)
#コメントアウトを外すとスケーリング後の値を確認できる
#print(train_mm)
#print(train_std)
#print(test_mm)
#print(test_std)
  • 次に、「K近傍法」「パーセプトロン」「ランダムフォレスト」を用いて、「元のデータ」「正規化したデータ」「標準化したデータ」の正解率を比較します。

1.K近傍法

  • 「新しいサンプルと特徴が似ているいくつかのサンプルのラベルを参考にして、新しいサンプルのラベルを予測する分類手法」とのこと。
  • 参考：Wikipedia K近傍法 
from sklearn.neighbors import KNeighborsClassifier
 
#元のデータ用
lr = KNeighborsClassifier()
#正規化したデータ用
lr_mm = KNeighborsClassifier()
#標準化したデータ用
lr_std = KNeighborsClassifier()

#元のデータの適用
lr.fit(train_x, train_y)
#正規化したデータの適用
lr_mm.fit(train_mm, train_y)
#標準化したデータの適用
lr_std.fit(train_std, train_y)

print('元のデータのスコア :',lr.score(test_x, test_y))
print('正規化したデータのスコア :',lr_mm.score(test_mm, test_y))
print('標準化したデータのスコア :',lr_std.score(test_std, test_y))
  • 比較すると元のデータのスコアだけが低く、正規化や標準化を行なったデータに対する正解率は0.9を超えています。
  • 上記から、正規化や標準化がK近傍法に有効であることが分かります。

2.パーセプトロン

  • K近傍法と同様にモデルのパラメータはデフォルトに設定されているものを使用します。

  • パーセプトロンは最近の機械学習分野において必須とも言える知識とのこと。確実に押さえておく必要あり。

  • パーセプトロンやニューラルネットワークについての知識はAIマガジンの今時のエンジニアが知っておくべきディープラーニングの基礎知識が参考になるようです。（後ほど確認します。）

  • 各データ用にパーセプトロンを定義し、データを定義します。

from sklearn.linear_model import Perceptron
 
#元のデータ用
lr = Perceptron(random_state = 0)
#正規化したデータ用
lr_mm = Perceptron(random_state = 0)
#標準化したデータ用
lr_std = Perceptron(random_state = 0)
 
#元のデータの適用
lr.fit(train_x, train_y)
#正規化したデータの適用
lr_mm.fit(train_mm, train_y)
#標準化したデータの適用
lr_std.fit(train_std, train_y)

print('元のデータのスコア :',lr.score(test_x, test_y))
print('標準化したデータのスコア :',lr_std.score(test_std, test_y))
print('正規化したデータのスコア :',lr_mm.score(test_mm, test_y))
  • 実行結果は、以下のとおりです。
  • 元のデータに対する正解率を見ると、K近傍法よりもさらに低くなっています。
  • もとの正規化や標準化を行なったデータに対する正解率は0.9を超えています。このことから正規化や標準化がパーセプトロンに有効であることが分かります。

3.ランダムフォレスト

  • ツリーベース型のモデルであるランダムフォレストを用いてワインの分類を行います。（ツリーベース型モデルは、正規化や標準化にそれほど影響されにくい。）
  • 各データ用にランダムフォレストを定義し、データを適用します。
from sklearn.ensemble import RandomForestClassifier
#元のデータ用
lr = RandomForestClassifier(random_state = 0)
#正規化したデータ用
lr_mm = RandomForestClassifier(random_state = 0)
#標準化したデータ用
lr_std = RandomForestClassifier(random_state = 0)
 
#元のデータの適用
lr.fit(train_x, train_y)
#正規化したデータの適用
lr_mm.fit(train_mm, train_y)
#標準化したデータの適用
lr_std.fit(train_std, train_y)
 

print('元データのスコア :',lr.score(test_x, test_y))
print('正規化データのスコア :',lr_mm.score(test_mm, test_y))
print('標準化データのスコア :',lr_std.score(test_std, test_y))
  • 実行結果は、以下のとおりです。
  • 元データのスコアが0.97。スコア0.9を超えているため、影響を受けにくいのは間違いない。
  • モデルによってスケーリングの影響は様々ということが分かりました。

考察

  • 今回は、データのスケーリング（標準化、正規化）を学びました、スケーリングするにあたり、複数のライブラリで実装できることが分かりました。
  • また、最後の方にはワインの分類で、いくつかのモデルを試しました。その過程でデータセットを学習用とテスト用に分割し、予測する一連の流れを経験し、少しづつ機械学習ぽくなってきた気がします。まだまだ、学ぶことも多いですが少しづつ学習を進めていきます。

参考

4
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
3