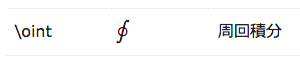きれいな数式がかけると見るのも書くのも気持ちがいいですよね!
QiitaではMathJaxというライブラリを使っていて、ブラウザ上で美しい数式を見ることができます。
MathJaxにおける数式の記述方法はTeX記法に則っています。
以下Qiitaにおける数式を書くためのチートシートです。
数式の記述方法
コードブロックの言語指定に math を指定することでTeX記法を用いて数式を記述することができます。
```math
e^{i\pi} = -1
```
e^{i\pi} = -1
また、$$で囲むことで独立した段落として記述することもできます。
\$\$ e^{i\theta} = \cos\theta + i\sin\theta $$
$$ e^{i\theta} = \cos\theta + i\sin\theta $$
その他にも数式を$で囲むことで埋め込み形式として記述できます
\$ e^{\pi i}= -1 $はオイラーの等式として知られています
$ e^{\pi i}= -1 $はオイラーの等式として知られています
改行(\\)
\displaylinesで数式を囲み、数式の行末に\\(バックスラッシュ2つ)をつけることによって改行をすることができます。
※2023/7/6のMathJaxのアップデートでバックスラッシュのみの改行の実装は検討されているものの未対応のようです
https://github.com/mathjax/MathJax/issues/2312
※2023/11/20追記. マークダウンの不具合?により引用内における改行のバックスラッシュが1つしか表示されておりません。実際に改行を行う際はバックスラッシュを2つ入れて記載してください
四則演算
```math
\displaylines{
1 + 2 = 3 \\
2 - 1 = 1 \\
3 \times 2 = 6 \\
6 \div 3 = 2
}
```
\displaylines{
1 + 2 = 3 \\
2 - 1 = 1 \\
3 \times 2 = 6 \\
6 \div 3 = 2
}
分数
```math
\displaylines{
\frac{1}{2} - \frac{1}{3} = \frac{1}{6} \\
\frac{a+b}{2ab}
}
```
\displaylines{
\frac{1}{2} - \frac{1}{3} = \frac{1}{6} \\
\frac{a+b}{2ab}
}
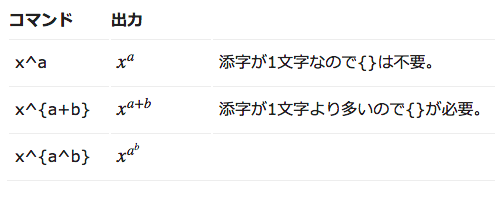
上付き・下付き文字
上付き文字
```math
ax^2 + bx + c = 0 \\
y = x^{\frac{1}{2}}
```
ax^2 + bx + c = 0 \\
y = x^{\frac{1}{2}}
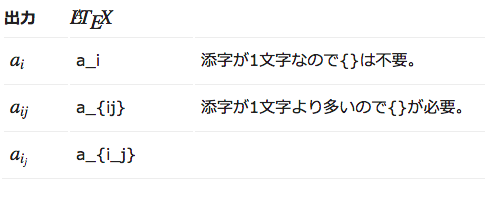
下付き文字
```math
x_{n+1} = rx_n(1-x_n)
```
x_{n+1} = rx_n(1-x_n)
イコール(=)を揃える
begin{align}とend{align}と&を用いることによってブロック内で改行前後の位置を揃える
```math
\begin{align}
f(x) &= x^2+3x+2 \\
&= (x+1)(x+2)
\end{align}
```
\begin{align}
f(x) &= x^2+3x+2 \\
&= (x+1)(x+2)
\end{align}
文字の間隔
一般的なスペース
```math
y \quad = ax \qquad + b
```
y \quad = ax \qquad + b
調整可能なスペース
```math
a \hspace{50pt} b \hspace{1cm} c
```
a \hspace{50pt} b \hspace{1cm} c
小さなスペース
```math
a \! b \, c \: d \; e \\
a \!\! b \,\, c \:\: d \;\; e
```
a \! b \, c \: d \; e \\
a \!\! b \,\, c \:\: d \;\; e
括弧の大きさ
下に行くほど括弧が大きくなる
左括弧
\bigl
\Bigl
\biggl
\Biggl
右括弧
\bigr
\Bigr
\biggr
\Biggr
丸括弧()・角括弧[]・波括弧{}を使いたいときは、それぞれの括弧の後ろにつける
```math
a \Biggl(
b \biggl(
c \Bigl(
d \bigl(
e ( f + g )
\bigr)
\Bigr)
\biggr)
\Biggr)
```
a \Biggl(
b \biggl(
c \Bigl(
d \bigl(
e ( f + g )
\bigr)
\Bigr)
\biggr)
\Biggr)
極限(lim)
```math
\lim_{x \to \infty} f(x) \\
\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\
\lim_{\substack{x \to \infty \ y \to \infty}} f(x,y)
```
\lim_{x \to \infty} f(x) \\
\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\
\lim_{\substack{x \to \infty \\ y \to \infty}} f(x,y)
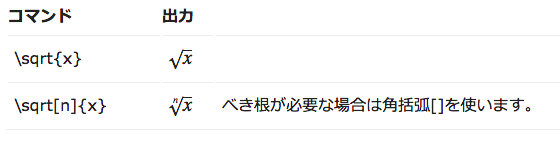
平方根(sqrt)
```math
\sqrt{a^2+b^2} \\
\sqrt[3]{a}
```
\sqrt{a^2+b^2} \\
\sqrt[3]{a}
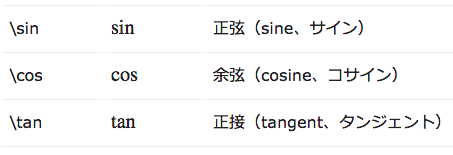
三角関数(sin, cos, tan)
```math
\sin^2 x + \cos^2 x = 1
```
\sin^2 x + \cos^2 x = 1
指数関数(e, exp)
```math
e^{i\pi} = -1 \\
e^{i\theta} = \cos \theta + i \sin \theta
```
e^{i\pi} = -1 \\
e^{i\theta} = \cos \theta + i \sin \theta
対数関数・自然対数(log, ln)
```math
\log_a \frac{x}{y} = \log_a x - \log_a y \\
\ln \frac{x}{y}
```
\log_a \frac{x}{y} = \log_a x - \log_a y \\
\ln \frac{x}{y}
積分・重積分・周回積分(∫)
積分
```math
\int f(x)dx \\
\int_{a}^{b}f(x)dx
```
\int f(x)dx \\
\int_{a}^{b}f(x)dx
重積分
```math
\iint f(x,y)dxdy
```
\iint f(x,y)dxdy
周回積分
```math
\oint_C \frac{1}{z}dz
```
\oint_C \frac{1}{z}dz
和・総和(シグマΣ)
```math
\sum_{k=1}^{n} k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} \\
\sum_{k=1}^{n} k^2 = 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}
```
\sum_{k=1}^{n} k = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} \\
\sum_{k=1}^{n} k^2 = 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}
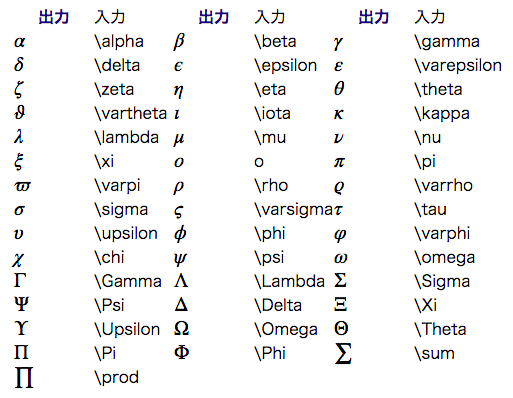
ギリシャ文字
```math
i \hbar \frac{\partial \psi}{\partial t} = H \psi(x,t)
```
i \hbar \frac{\partial \psi}{\partial t} = H \psi(x,t)
等号、不等号、演算子、集合
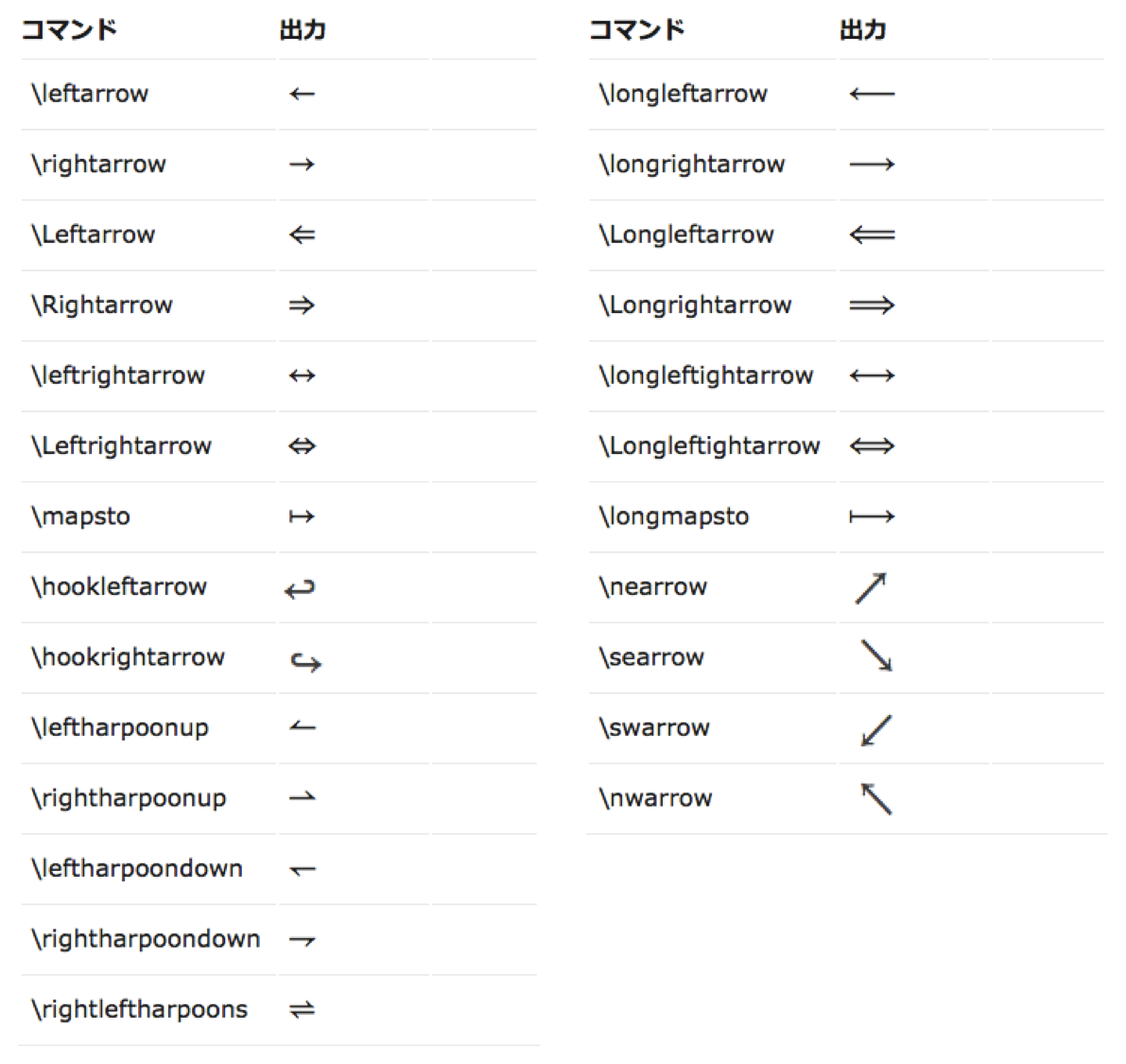
矢印記号
```math
\begin{align}
\qquad &ax^2+bx+c = 0 \\
\Leftrightarrow &\quad x^2 + \frac{b}{a}x = - \frac{c}{a} \\
\Leftrightarrow &\quad x^2 + \frac{b}{a} x + \frac{b^2}{4a^2} = \frac{b^2}{4a^2} - \frac{c}{a} \
\Leftrightarrow &\quad (x + \frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2} \\
\Leftrightarrow &\quad x + \frac{b}{2a} = \pm \frac{\sqrt{b^2-4ac}}{2a} \\
\therefore &x = \frac{-b \pm \sqrt{b^2-4ac} }{2a}
\end{align}
```
\begin{align}
\qquad &ax^2+bx+c = 0 \\
\Leftrightarrow &\quad x^2 + \frac{b}{a}x = - \frac{c}{a} \\
\Leftrightarrow &\quad x^2 + \frac{b}{a} x + \frac{b^2}{4a^2} = \frac{b^2}{4a^2} - \frac{c}{a} \\
\Leftrightarrow &\quad (x + \frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2} \\
\Leftrightarrow &\quad x + \frac{b}{2a} = \pm \frac{\sqrt{b^2-4ac}}{2a} \\
\therefore &x = \frac{-b \pm \sqrt{b^2-4ac} }{2a}
\end{align}
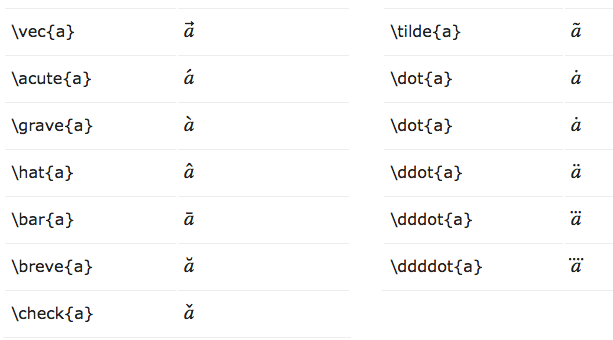
アクセント記号(ベクトルなど)
```math
\vec{A} = \vec{B} + \vec{C} \\
F = m\ddot{x}
```
\vec{A} = \vec{B} + \vec{C} \\
F = m\ddot{x}
ドット(3点リーダー)
```math
\left(
\begin{array}{ccccc}
a_{11} & \cdots & a_{1i} & \cdots & a_{1n} \\
\vdots & \ddots & & & \vdots \\
a_{i1} & & a_{ii} & & a_{in} \\
\vdots & & & \ddots & \vdots \\
a_{n1} & \cdots & a_{ni} & \cdots & a_{nn}
\end{array}
\right)
```
\left(
\begin{array}{ccccc}
a_{11} & \cdots & a_{1i} & \cdots & a_{1n}\\
\vdots & \ddots & & & \vdots \\
a_{i1} & & a_{ii} & & a_{in} \\
\vdots & & & \ddots & \vdots \\
a_{n1} & \cdots & a_{ni} & \cdots & a_{nn}
\end{array}
\right)
行列と行列式
```math
\begin{matrix}
a & b \\
c & d
\end{matrix}
```
\begin{matrix}
a & b \\
c & d
\end{matrix}
```math
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
```
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
```math
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
```
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
```math
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}
```
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}
```math
\begin{Vmatrix}
a & b \
c & d
\end{Vmatrix}
```
\begin{Vmatrix}
a & b \\
c & d
\end{Vmatrix}
```math
\begin{pmatrix}
a & b \
c & d
\end{pmatrix}
\times
\begin{vmatrix}
e & f \
g & h
\end{vmatrix}
```
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\times
\begin{vmatrix}
e & f \\
g & h
\end{vmatrix}
場合分け
```math
f(x) = \left\{
\begin{array}{ll}
1 & (x \geq 0) \
0 & (x \lt 0)
\end{array}
\right.
```
f(x) = \left\{
\begin{array}{ll}
1 & (x \geq 0)\\
0 & (x \lt 0)
\end{array}
\right.