背景・目的
私は、現在データエンジニアリングを生業としています。普段は、データ基盤の構築や、パフォーマンスチューニングなどビックデータに関する業務に従事しています。
ビックデータの収集や、蓄積、分析などの環境構築の経験はそこそこありますが、機械学習による予測や分類などのスキルは持ち合わせていませんでした。
今まで機械学習を避け続けてきましたが、一念発起し学ぼうと思います。
学び方としては、AWS Certified Machine Learning – Specialty(以降、ML試験という。)の勉強を通して、理解を深めていきます。ML試験のガイドの第2分野に、探索的データ解析が登場しましたのでそこから学びたいと思います。
今回は、以下のうちデータのビニングについて学びたいと思います。
特徴エンジニアリングの概念を分析/評価する (データのビニング、トークナイゼーション、外れ値、合成的特徴、One-Hot エンコーディング、次元低減)
なお、過去の機械学習の調べてみたシリースは下記にまとめています。
-
2.探索的データ分析
-
2.1.モデリング用のデータをサニタイズおよび準備する
-
2.2.特徴エンジニアリングを実行する
-
機械学習プロセス
まとめ
- データのビニングとは、値を並べ一定の数で分割します。
- Pandasを利用することで簡単に実装できます。
- 値で分割するcutと要素数で分割するqcutをしようすることで、実現できます。
概要
データのビニング
Wikipediaによると、
「対象物をある集合(「ビン」)に分配、集約する作業手順を指す。」とのこと。
より一般的なデータ処理におけるビニングは、離散化とも言い、データの濃度を減らすための前処理手法の一つである[2]。ビニングを行うことで、データに含まれる誤差や分散といった「雑音」を排して適切な値を補完し、見通しを良くすることで、データから構成するモデルの質を向上させる可能性がある[7][2]。
- データのビニングを離散化ともいう。
- 前処理で実施する手法の一つ。ビニングを行うことで誤差などの雑音を除き適切な値を保管する。その結果、モデルの質が向上するようです。
手法
ビニングは、規則的に並んでいるデータの値を、隣接する値との間で評価し、適当な値で置換することで、データの局所的な平滑化を実現し、モデルの構成を容易にすることを狙う。規則的に並ぶデータは、いくつかの区間・階層、即ち「ビン」に配分され、各ビンの中で適当な値により平滑化する[7]。ビンの区切り方には、標本数を一定にする分位数で区切る方法、値の範囲を一定にする固定幅を用いる方法がある。値の置換方法としては、ビンの中の平均値や中央値を採用する方法、ビンの中の標本のうち最大値・最小値を「境界値」として近い方の境界値を採用する方法、などがある[7]。ビニングは、データを集約してデータ数を減らし高次の階層とすることで、概念階層を構築する手法としても用いることができる。この手続きは、決定木のような機械学習のアルゴリズムにも必要なものである[7]。
- 規則的に並ぶデータを隣接する値との間で評価して、適当な値で置換する。
- ビンに配分する方法は、いくつかの区間、階層に配分し、ビンの中で適当な値により平準化する。
- ビンの区切り方は、以下のようなものがある。
- 標本数を一定にする分位数
- 相対の範囲を一定にする固定幅
- 価の置換方法は、以下のようなものがある。
- ビンの中の平均値、中央値を採用する
- ビンの中の標本内のうち最大値、最小値を境界値として近い方の境界値を採用する
- データを集約してデータ数を減らし、高次の階層とすることで概念階層を構築する手法としても用いることができる。(これはイメージがつかない。。)
実践
こちらのブログを参考に手を動かして、確認します。(わかりやすいです。ありがとうございます!)
pandasでビニング処理を行うには、pandasを使用するとのことです。
- 値を元にビン分割する。
cut() - 量を元にビン分割する。
qcut()
使用方法を以下に整理します。
| 目的 | サブカテゴリ | 関数 |
|---|---|---|
| 等分割または任意の境界値を指定してビニング処理をする。 | 最大値と最小値の間を等間隔で分割 | cut() |
| 境界値を指定して分割 | cut() | |
| 境界値のリストを取得: 引数 | retbins | |
| 左右どちらのエッジを含めるか指定: 引数 | right | |
| ラベルを指定: 引数 | labels | |
| 境界値の精度(小数点以下の桁数)を指定: 引数 | precision | |
| ビンに含まれる要素数を等しくビニング処理 | 分割数を指定して分割 | qcut() |
| 値が重複している場合の注意 | qcut() | |
| ビンに含まれる要素数をカウント: | - | value_counts() |
事前準備
- ここでは、PandasのSeriesを使用します。
- Series
- シリーズ
- 1次元のデータ構造を操作します。
- DataFrame
- データフレーム
- 2次元のデータ構造を操作します。
コード
# ライブラリのインポート
import pandas as pd
# 11回のループを回し、1^2、2^2、3^2・・・のように2乗した値と、abcd・・・のインデックスを設定しています。
s = pd.Series(data=[x**2 for x in range(11)],
index=list('abcdefghijk'))
print(s)
結果
- 0から10までの値をそれぞれ二乗されたものが,
- 一次元のデータ構造として格納されたのが分かります。
| インデックス | 元の値 | 格納された値 | 備考 |
|---|---|---|---|
| a | 0 | 0 | |
| b | 1 | 1 | |
| c | 2 | 4 | |
| d | 3 | 9 | |
| e | 4 | 16 | |
| f | 5 | 25 | |
| g | 6 | 36 | |
| h | 7 | 49 | |
| i | 8 | 64 | |
| j | 9 | 81 | |
| k | 10 | 100 |
等分割または任意の境界値を指定してビニング処理: cut()
- pandas.cut()関数では、以下の引数を指定します。
- 第一引数xに元データとなる一次元配列(Pythonのリストやnumpy.ndarray, pandas.Series)
- 第二引数binsにビン分割
最大値と最小値の間を等間隔で分割
第二引数binsに整数値を指定すると分割数(ビン数)の指定になります。
- 最大値と最小値の間を等間隔で分割します。
- pandas.Seriesを元データとした場合、pandas.Seriesが返ります。
コード
- 以下は、4分割している例
# sは、事前準備したコード、4は分割数。
s_cut = pd.cut(s, 4)
print(s_cut)
print(type(s_cut))
結果
結果は、以下のとおりです。
- (a, b]はa < x <=bの意味です。
- デフォルトでは左側(小さい方)のエッジの値は含まれません。
- 最小の境界値は最大値の0.1%分小さい値になります。
以下のようにビニングされました。
| インデックス | 値 | ビン |
|---|---|---|
| a | 0 | 0から25 |
| b | 1 | 0から25 |
| c | 4 | 0から25 |
| d | 9 | 0から25 |
| e | 16 | 0から25 |
| f | 25 | 0から25 |
| g | 36 | 26から50 |
| h | 49 | 26から50 |
| i | 64 | 51から75 |
| j | 81 | 76から100 |
| k | 100 | 76から100 |
※ 大雑把に表現したいため、小数点は省略しています。
境界値を指定して分割
第二引数binsにリストを指定すると、リストの要素を境界値として分割されます。範囲外の値はNaNとなります。
コード
- 0から10、11から50、51から100でビニングされます。
print(pd.cut(s, [0, 10, 50, 100]))
結果
以下のようにビニングされました。
0,10,50,100と指定してますが、最初の0から10では、0 < 値 <= 10となるため、インデックス0はNaNになっています。
上述した、等間隔で分割では、最小の境界値は-0.1されるとのことでしたが、値を指定した場合では挙動が変わるようです。
| インデックス | 値 | ビン |
|---|---|---|
| a | 0 | NaN |
| b | 1 | 0から10 |
| c | 4 | 0から10 |
| d | 9 | 0から10 |
| e | 16 | 10から50 |
| f | 25 | 10から50 |
| g | 36 | 10から50 |
| h | 49 | 10から50 |
| i | 64 | 50から100 |
| j | 81 | 50から100 |
| k | 100 | 50から100 |
※ 大雑把に表現したいため、小数点は省略しています。
境界値のリストを取得: 引数retbins
引数retbins=Trueとすると、ビン分割されたデータと境界値のリストを同時に取得できます。
境界値のリストはnumpy.ndarray形式でリターンされます。
コード
以下の例では、戻り値の左のs_cutでは、従来どおり分割された範囲が返されます。右側のbinsでは
# 4分割、第3引数にretbins=Trueを指定
s_cut, bins = pd.cut(s, 4, retbins=True)
print("-- s_cut --")
print(s_cut)
print("-- bins --")
print(bins)
print("-- type --")
print(type(bins))
結果
左右どちらのエッジを含めるか指定: 引数right
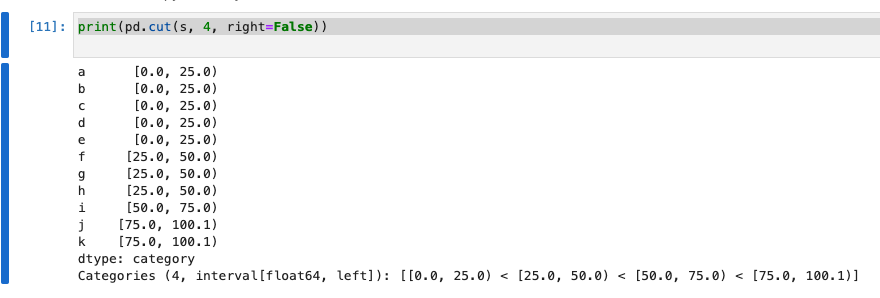
- デフォルトでは右のエッジがビンに含まれ左のエッジがビンに含まれないが、引数right=Falseとすると、逆に右のエッジがビンに含まれなくなる。
- つまり、(a, b]はa <= x <=bになるということ。
コード
print(pd.cut(s, 4, right=False))
結果
以下のようにビニングされました。また、right=Falseによって、今度は、最大値のほうが+0.1されることが分かります。
| インデックス | 値 | ビン | 備考 |
|---|---|---|---|
| a | 0 | 0から24 | |
| b | 1 | 0から24 | |
| c | 4 | 0から24 | |
| d | 9 | 0から24 | |
| e | 16 | 0から24 | |
| f | 25 | 25から49 | ※変更点。さきほどは1つのビンに入っていました。 |
| g | 36 | 25から49 | |
| h | 49 | 25から49 | |
| i | 64 | 25から49 | |
| j | 81 | 76から100 | |
| k | 100 | 76から100 |
ラベルを指定: 引数labels
引数labelsでラベルを指定できます。デフォルトはlabels=Noneで、これまでの例の通り(a, b]となります。
labels=Falseにすることで、整数値のインデックス(0始まりの連番)になります。
コード
print(pd.cut(s, 4, labels=False))
結果
- ビンのレンジが何番目のビンか表示されました。
| インデックス | 値 | ビン(実際は表示されていません。) | ビンのラベル |
|---|---|---|---|
| a | 0 | 0から25 | 0 |
| b | 1 | 0から25 | 0 |
| c | 4 | 0から25 | 0 |
| d | 9 | 0から25 | 0 |
| e | 16 | 0から25 | 0 |
| f | 25 | 0から25 | 0 |
| g | 36 | 26から50 | 1 |
| h | 49 | 26から50 | 1 |
| i | 64 | 51から75 | 2 |
| j | 81 | 76から100 | 3 |
| k | 100 | 76から100 | 3 |
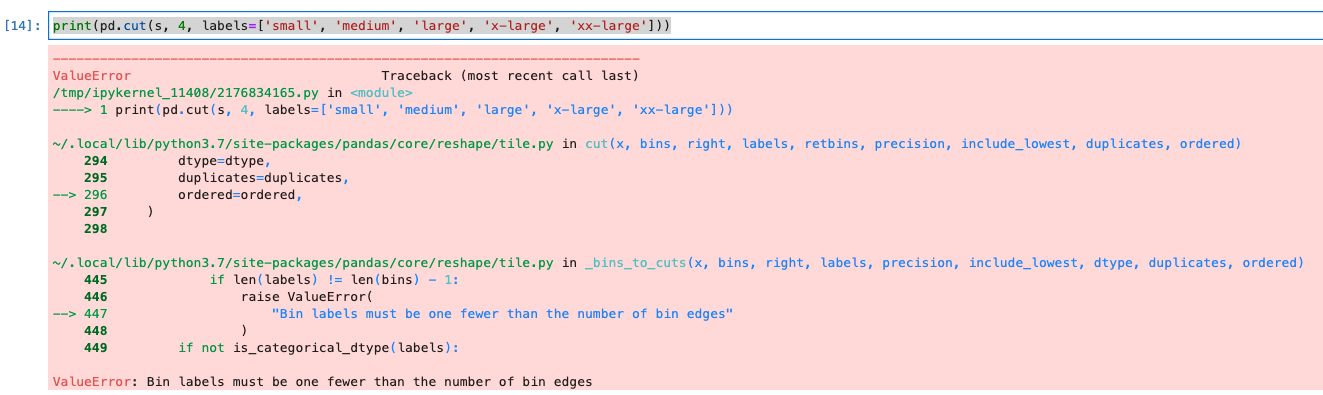
ラベルを指定: 引数labels(ラベル名の指定)
ラベル名もリストで指定ができます。このとき、ラベルの数とビンの数が一致していないとエラーになります。
コード(一致する場合)
print(pd.cut(s, 4, labels=['small', 'medium', 'large', 'x-large']))
結果(一致する場合)
コード(一致しない場合)
print(pd.cut(s, 4, labels=['small', 'medium', 'large', 'x-large', 'xx-large']))
結果(一致しない場合)
境界値の精度(小数点以下の桁数)を指定: 引数precision
引数precisionを使用することで、境界値の精度(小数点以下の桁数)を指定できます。
コード
print(pd.cut(s, 3))
# 小数点1桁の精度
print(pd.cut(s, 3, precision=1))
結果
以下のように、ビニングされました。
| インデックス | 値 | ビンの範囲(デフォルト) | ビンの範囲(精度指定あり) |
|---|---|---|---|
| a | 0 | -0.1から33.333 | -0.1から33.3 |
| b | 1 | -0.1から33.333 | -0.1から33.3 |
| c | 4 | -0.1から33.333 | -0.1から33.3 |
| d | 9 | -0.1から33.333 | -0.1から33.3 |
| e | 16 | -0.1から33.333 | -0.1から33.3 |
| f | 25 | -0.1から33.333 | -0.1から33.3 |
| g | 36 | 33.333から66.667 | 33.3から66.7 |
| h | 49 | 33.333から66.667 | 33.3から66.7 |
| i | 64 | 33.333から66.667 | 33.3から66.7 |
| j | 81 | 66.667から100.0 | 66.7から100.0 |
| k | 100 | 66.667から100.0 | 66.7から100.0 |
ビンに含まれる個数(要素数)を等しくビニング処理: qcut()
qcut()はcut()のように値に対して等分割したり境界値を指定するのではありません。各ビンに含まれる個数(要素数)が等しくなるようにビニング処理(ビン分割)する関数です。
以下の引数を渡します。
- 第一引数xに元データとなる一次元配列(Pythonのリストやnumpy.ndarray, pandas.Series)を指定
- 第二引数qに分割数を指定
なお、cut()と同じ引数としてlabels, retbinsがあります。
分割数を指定して分割
第二引数qに分割数を指定します。q=2とすると中央値で分割されます。
コード
print(pd.qcut(s, 2))
結果
cutの場合は?
print(pd.cut(s,2))
| インデックス | 値 | ビン(qcut:要素数を元に分割) | ビン(cut:最小値、最大値をもとに値で分割) | 備考 |
|---|---|---|---|---|
| a | 0 | -0.001から25.0 | -0.1から50.0 | |
| b | 1 | -0.001から25.0 | -0.1から50.0 | |
| c | 4 | -0.001から25.0 | -0.1から50.0 | |
| d | 9 | -0.001から25.0 | -0.1から50.0 | |
| e | 16 | -0.001から25.0 | -0.1から50.0 | |
| f | 25 | -0.001から25.0 | -0.1から50.0 | |
| g | 36 | 25.0から100.0 | -0.1から50.0 | |
| h | 49 | 25.0から100.0 | -0.1から50.0 | |
| i | 64 | 25.0から100.0 | 50.0から100.0 | |
| j | 81 | 25.0から100.0 | 50.0から100.0 | |
| k | 100 | 25.0から100.0 | 50.0から100.0 |
- 上記から、以下のことが分かります。(qcut、cutの違いがわかりました。)
- qcutは、11個の要素があり、0番目から5番目、6番目から10番目まで2分割されている。
- cutは、最小値と最大値をもとに、0番目から7番目、8番目から9番目まで2分割されている。
四分位
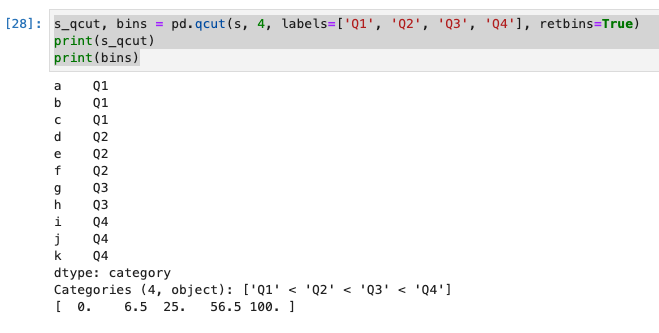
q=4とすると四分位数ごとに分割される。上述のようにcut()と同じ引数としてlabels, retbinsが使えます
コード
s_qcut, bins = pd.qcut(s, 4, labels=['Q1', 'Q2', 'Q3', 'Q4'], retbins=True)
print(s_qcut)
print(bins)
結果
値が重複している場合の注意
元データの要素の値が重複している場合は注意が必要とのことです。例えば中央値までが重複した値である場合では、以下のようになります。
コード
s_duplicate = pd.Series(data=[0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6],
index=list('abcdefghijk'))
print(s_duplicate)
結果
コード
print(pd.qcut(s_duplicate, 2))
print(pd.qcut(s_duplicate, 4))
結果
- 最小値、1/4分位数(25%)、中央値(50%)、3/4分位数(75%)、最大値が境界値として設定されるが、例のように重複した要素が多いと、最小値と1/4分位数が同じ値になってしまうのがエラーの原因とのことです。
重複を除去して分割すると解消される
コード
print(pd.qcut(s_duplicate, 4, duplicates='drop'))
結果
ビンに含まれる個数(要素数)をカウント: value_counts()
- cut()やqcut()で取得できるビン分割してラベル付けされたpandas.Seriesからvalue_counts()メソッドを使用することで、ビンに含まれる個数(要素数)が取得できます。
コード
counts = pd.cut(s, 3, labels=['S', 'M', 'L']).value_counts()
print(type(counts))
print(counts['M'])
結果
考察
今回は、ビニング処理を試してみました。ビニング処理は四分位やパーセンタイルなどに利用できることが分かった気がします。
ただし、これを機械学習でどの様に活用していくかは、まだ想像がつきません。引き続き理解を深めていきたいと思います。
参考