【Python演算処理】冪算(Exponentiation/Logarithmicion)と乗除算(Multiplying and Dividing)の関係について。

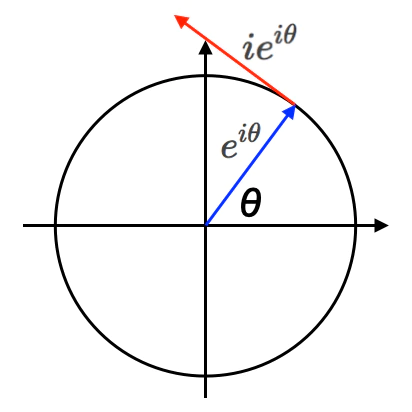
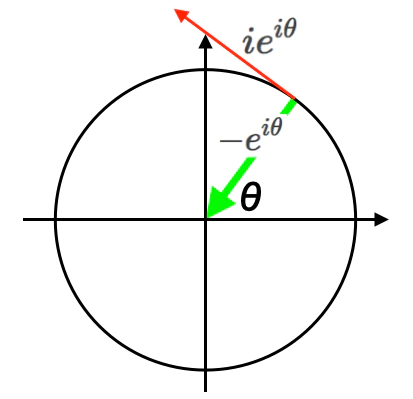
まずは基本中の基本たる関数概念(Function Concept)そのものの定義について振り返っておきましょう。
関数 (数学) - Wikipedia

二つの数の集合X,Yがあって、Xの要素xに対してYの要素yがただ一つ定まる時、この対応を関数(Function)と呼びy=f(x)などと書き表す(fはfunctionの略だが、複数の関数への言及が不可避となる状況ではそれをy=g(x),y=h(x)などと呼び分ける)。

• この時xを独立変数(Independent Variable)、yを従属変数(Dependent Variable)と呼ぶ。
• また集合Xを関数fの定義域(Domain)、集合Yの部分集合$(y|y=f(x),x \in X)$をこの関数の値域(Range)という。

関数y=fxの変化の様子はxの値を横座標、yの値を縦座標としxを定義域内で変化させた時の点P(x,y)の軌跡を描くと一目瞭然となる。これが関数y=f(x)のグラフである。

【Pyrhon演算処理】同心集合③環概念と指数/対数写像概念の導入

①群論でいう加法実数群(Additive Real Group)だと、主に加法単位元(Additive Identity)0を中心に+∞から-∞の範囲かけての均等尺(Even Scale)が定義域や値域に指定される。
【Pyrhon演算処理】同心集合②加法的同心集合とは？

②同じくその指数写像(Exponential Map)たる乗法実数群(Multiplicative Real Group)だと、主に乗法単位元(Multiplicative Identity)1を中心に0から∞の範囲にかけての対数尺(Logarithmic Scale)が定義域や値域に指定される。
【Pyrhon演算処理】同心集合①乗法的同心集合とは？

群同型 Wikipedia

加法実数群$(\mathbb{R},+)$は、すべての正の実数が乗法についてなす群$(\mathbb {R}^+,×)$に、同型写像$f(x)=e^x(x \in \mathbb{R})$によって同型である：

(\mathbb {R},+) \cong (\mathbb{R}^{+},×)

• この定義により加法実数群と乗法実数群は群同型(Group Isomorphism)と見做されるので理論上実数環(Real Ring)として統合的に扱う事も可能とされる。
  【Python演算処理】環論に立脚した全体像再構築①空環と実数環

③極座標系(Polar Coordinate System)$(r,φ),(r,φ,θ),e^{iθ}=cos(θ)+sin(θ)i$などでは、主に2πラジアンを1周期とする半径rの角度空間(Angle Space)が定義域や値域に指定される。

群同型 Wikipedia

加法整数群$(\mathbb {Z},+)$は加法実数群$(\mathbb{R},+)$の部分群であり、商群$\frac{\mathbb{R}}{\mathbb{Z}}$は、同型写像$f(x+\mathbb {Z})=e^{2πxi}(x \in \mathbb{R})$(x=0→2π)によって絶対値1の乗法複素数群$S^1$に同型である：

\frac{(\mathbb{R},+)}{(\mathbb{Z},+)} \cong S^1

• この定義により角度空間概念も実数環の有する性質の一つとして統合的に扱える様になるが、関数の対象としてはそれがしばしば見せる多価性(Multivalued)が問題となる。複素解析論（Complex Analysis Theory）において方便として「分岐截断(Branch Point Cut)」の概念が導入されたのはこの問題に対応する為であった(その経緯上、リーマン球面概念同様、群論的には乗法群にのみに関わってくるとも考えられそうである)。
  分岐点 (数学) - Wikipedia

• 群論では、ここでいう絶対値1の乗法複素数群=1次元球面(半径1の単位円)にリー群$S^1$(1次元トーラス)、円周群(Circle Group)$\mathbb{T}$、特殊直交群(Special Orthogonal Group)SO(2)、複素1次ユニタリ群(Unitary Group)U(1)といった様々な名前を与え、それぞれの発展形を展開する。
  リー群 - Wikipedia
  円周群 - Wikipedia
  直交群 - Wikipedia
  ユニタリ群 - Wikipedia

\mathbb{T}=SO(2)=U(1)=S^1=(z \in \mathbb{T}:|z|=1)

• また実数環を垂直軸z(高さh)に加法実数群、水平軸xy(半径rの極座標系)に乗法実数群を配した円筒座標系(Cylindrical Coordinate System)としてイメージする場合、そこに配された球表面の指数写像の取り方に「(地図投影法におけるメルカトル図法に対応する)側面射影法」と「(地図投影法における正距方位図法に対応する)底面射影法」の2種類が存在する事に留意しなければならない。前者の写像は「高さπ、幅2πの矩形」、後者の写像は「半径πの円盤」となり、関数ではこれが定義域や値域に指定される。
  【Python画像処理】メルカトル図法と正距方位図法
  
  
  
  
  
  

④統計学（Statistics）の世界では「面積の合計が1となる矩形」を想定し、そのx軸に平均値0を中心に＋∞から-∞の範囲で均等尺を振った説明変数(Explanatory Variable)、y軸に指定した範囲の面積計算がそのままその区画の分布確率=p値となる目的変数(Response Variable)を配したグラフが良く使われ、それがそのままそれらを扱う関数の定義域や値域に指定される事が多い。
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間

なるほど、全体像を俯瞰するとこんな感じに繋がってたんですね。

#冪算(Exponentiation/Logarithmicion)と乗除算(Multiplying and Dividing)の関係

冪算(Exponentiation/Logarithmicion)$y=x^n$および$y=x^{\frac{1}{n}}$と乗算(Multiplying)$y=nx$および除算(Dividing)$\frac{x}{n}$の関係は以下となっています。

##勾配概念(Gradient Concept)の導入

傾き (数学) - Wikipedia

傾きmは傾斜角θによりm=tan(θ)と定義される。また平面上の直線の傾きは、垂直移動距離Δy($y_2-y_1$)を水平移動距離Δx($x_2-x_1$)で割ったm=Δy/Δxで定義される。

これらの等式が示す様に鉛直線（y軸に平行な直線）の傾きは、零除算となり、定義されない。

• $y=\lim_{n \to ∞}\frac{±x}{n^n}=0$の場合…一次関数(Linear Function)y=±axの勾配(Gradient)aが1から0にかけて推移するイメージ。

①n=1の時、奇関数y=±xとなる。

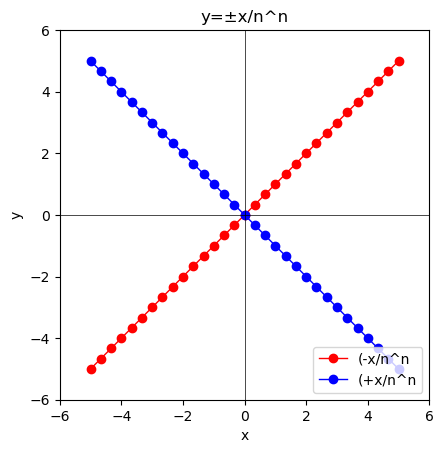
②これがnの増大につれ偶関数y=0に限りなく近付いていく。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#放物線x
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    yp= x/Time_Code[n]**Time_Code[n]
    ym= -x/Time_Code[n]**Time_Code[n]
    #描画
    plt.plot(x,yp,color="red",marker="o",lw=1,label="(-x/n^n")
    plt.plot(x,ym,color="blue",marker="o",lw=1,label="(+x/n^n")
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=±x/n^n")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(0)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin001.gif", writer="pillow")

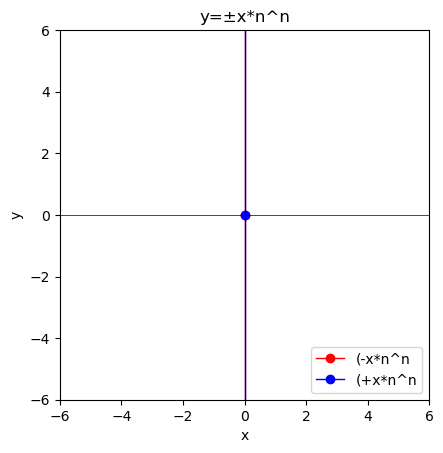
• $y=\lim_{n \to ∞}±x*n^n=∞$の場合…一次関数(Linear Function)y=±axの勾配(Gradient)aが1から∞にかけて推移するイメージ。

①n=1の時はやはり奇関数y=±xとなる。

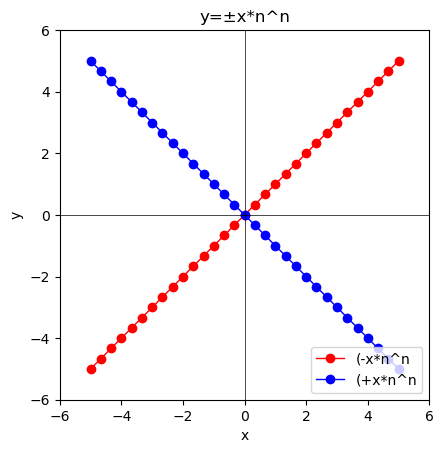
②これがnの増大につれ偶関数x=0に限りなく近付いていくイメージ。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#放物線x
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    yp= x*Time_Code[n]**Time_Code[n]
    ym= -x*Time_Code[n]**Time_Code[n]
    #描画
    plt.plot(x,yp,color="red",marker="o",lw=1,label="(-x*n^n")
    plt.plot(x,ym,color="blue",marker="o",lw=1,label="(+x*n^n")
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=±x*n^n")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(0)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin501.gif", writer="pillow")

ここには2種類の関数(Function)の射映(Projection)が重なって現れてきます。

###乗除算(Multiplying and Dividing)の射映
デカルト座標系(Cartesian Coordinate System)(x,y)上に描かれる同心円は、上掲の勾配概念(Gradient Concept)の制約故にそれぞれ対角線上に位置する(第一象限,第三象限)上と(第二象限,第四象限)上の展開が切り離されている。

	関数y=f(x)	任意の定義域xに対する値域y
0	y=±x/±∞	0
1	y=±x	座標(x,y)=(1,1)(-1,-1),(-1,1)(1,-1),
2	y=x*±∞	座標(x,y)=(∞,∞)(-∞,-∞),(-∞,∞)(∞,-∞)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["y=±x/±∞","y=±x","y=x*±∞"],
    ["0","座標(x,y)=(1,1)(-1,-1),(-1,1)(1,-1),","座標(x,y)=(∞,∞)(-∞,-∞),(-∞,∞)(∞,-∞)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['関数y=f(x)', '任意の定義域xに対する値域y'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

この辺りの四象限との関係は、おそらく線形代数(Linear Algebra)における行列演算(Matrix Aperation)の概念と関係してくるのです。
【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 1\\1 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}\left(a + b\right)^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 1\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 0\\1 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 0\\0 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}b^{2}\end{matrix}\right]

###冪算(Exponentiation/Logarithmicion)の射映
極座標系(Polar Coordinate System)(r,θ)上に同心円を描く。

	関数y=f(x)	任意の定義域±xに対する値域y
0	y=x^-∞=x/∞	0
1	y=x^0	1
2	y=x^∞	∞

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["y=x^-∞=x/∞","y=x^0","y=x^∞"],
    ["0","1","∞"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['関数y=f(x)', '任意の定義域±xに対する値域y'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

冒頭の定義に従うなら乗法実数群そのものに対応。

##指数関数(Exponential Function)と対数関数(Logarithmic Function)概念の導入

不思議にも以下の計算がpythonの冪乗算＊＊では実現出来ないのです。
np.arrayの累乗でRuntime warningが発生する
それでここでは複素数演算$xi^n$の実数部だけ取り出す形で計算しています。
【Rで球面幾何学】そもそも複素数Xi（x*(0+1i)）はどう振る舞う？

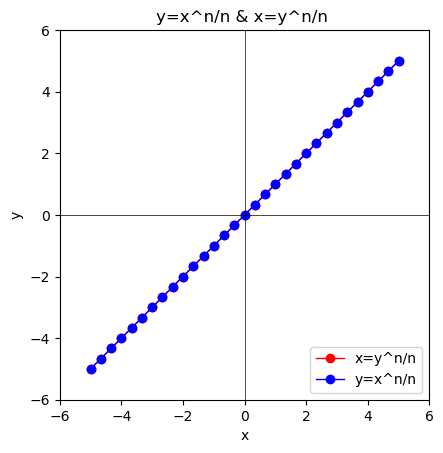
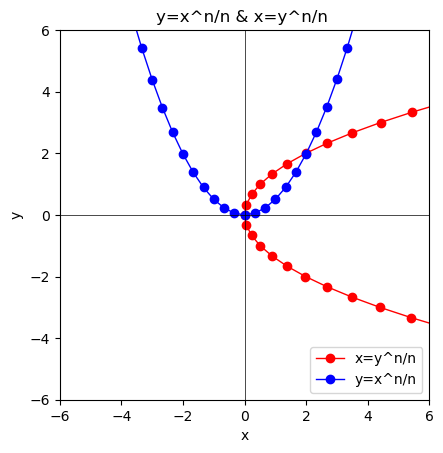
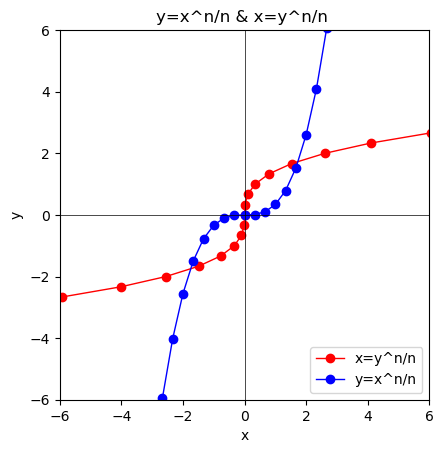
• $y=\lim_{n \to ∞}\frac{x^n}{n}$あるいは$x=\lim_{n \to ∞}\frac{y^n}{n}$の場合…前者が指数関数(Exponential Function)$y=x^n$、後者が対数関数(Logarithmic Function)$x=y^n(\log_{x}(n))$に対応します。

y=\lim_{n \to ∞}\frac{x^n}{n} = \left\{
\begin{array}{ll}
0 & (-1 \leqq x \leqq 1)  \\
∞ & (x>1)  \\
±∞ & (x<-1)
\end{array}
\right.\\
x=\lim_{n \to ∞}\frac{y^n}{n} = \left\{
\begin{array}{ll}
0 & (-1 \leqq y \leqq 1)  \\
∞ & (y>1)\\
±∞ & (y<-1)\\
\end{array}
\right.\\

①n=1の時、y=xとx=yが重なる。

②n=2の時、偶関数系の$y=\frac{x^2}{2}$ないしは$x=\frac{y^2}{2}$となり、両者は座標(x,y)=(2,2)で交わる。

③n=3の時、奇関数系の$y=\frac{x^3}{3}$ないしは$x=\frac{y^3}{3}$となり、この調子で両者の交点は座標(x,y)=(1,1)(-1,-1)に近づき続ける。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#複素数
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    #c1=(-x*(1+0j))**Time_Code[n]/Time_Code[n]
    #y1=c1.real
    c2=((x*(1+0j))**Time_Code[n])/Time_Code[n]
    y2=c2.real
    #yp= np.power(x, Time_Code[n])/Time_Code[n]
    #ym=np.power(-x, Time_Code[n])/Time_Code[n]
    #yp= (np.power(abs(x), Time_Code[n]) * np.sign(x))/Time_Code[n]
    #ym= (np.power(abs(-x), Time_Code[n]) * np.sign(-x))/Time_Code[n]
    #ym= -x**Time_Code[n]/Time_Code[n]
    #描画
    plt.plot(y2,x,color="red",marker="o",lw=1,label="x=y^n/n")
    plt.plot(x,y2,color="blue",marker="o",lw=1,label="y=x^n/n")
    #plt.plot(-x,ym,color="red",marker="o",lw=1)
    #plt.plot(x,yp,color="blue",marker="o",lw=1,label="x^n/n")
    #plt.plot(-x,yp,color="blue",marker="o",lw=1)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=x^n/n & x=y^n/n ")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(0)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin006.gif", writer="pillow")

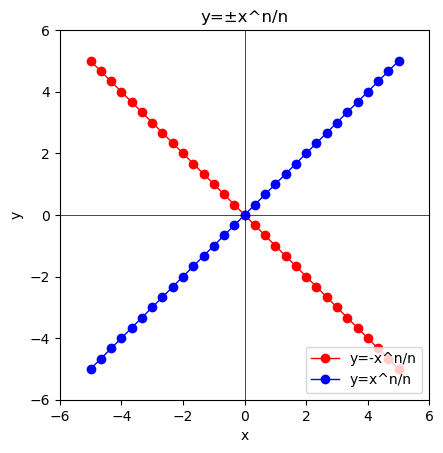
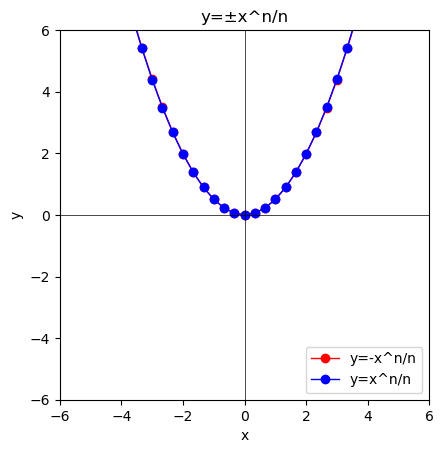
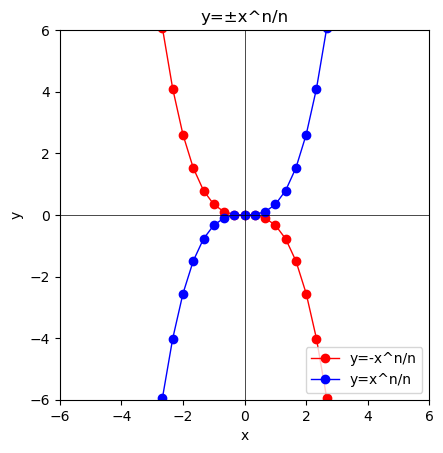
この0と±∞の峻別は$y=\lim_{n \to ∞}\frac{±x^n}{n}$の形で眺めても興味深いです。

y=\lim_{n \to ∞}\frac{x^n}{n} = \left\{
\begin{array}{ll}
0 & (-1 \leqq x \leqq 1)  \\
∞ & (x>1)  \\
±∞ & (x<-1)
\end{array}
\right.\\
y=\lim_{n \to ∞}\frac{-x^n}{n} = \left\{
\begin{array}{ll}
0 & (-1 \leqq y \leqq 1)  \\
∞ & (x<-1)\\
\mp ∞ & (x>1)\\
\end{array}
\right.\\

①n=1の時、y=±xとなる。

②n=2の時、偶関数系の$y=\frac{±x^2}{2}$が重なる。

③n=3の時、奇関数系の$y=\frac{±x^3}{3}$となり、この繰り返しで両者がそれぞれ上掲の極限に到達する。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#複素数
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    #c1=(-x*(1+0j))**Time_Code[n]/Time_Code[n]
    #y1=c1.real
    c2=((x*(1+0j))**Time_Code[n])/Time_Code[n]
    y2=c2.real
    #yp= np.power(x, Time_Code[n])/Time_Code[n]
    #ym=np.power(-x, Time_Code[n])/Time_Code[n]
    #yp= (np.power(abs(x), Time_Code[n]) * np.sign(x))/Time_Code[n]
    #ym= (np.power(abs(-x), Time_Code[n]) * np.sign(-x))/Time_Code[n]
    #ym= -x**Time_Code[n]/Time_Code[n]
    #描画
    plt.plot(-x,y2,color="red",marker="o",lw=1,label="y=-x^n/n")
    plt.plot(x,y2,color="blue",marker="o",lw=1,label="y=x^n/n")
    #plt.plot(-x,ym,color="red",marker="o",lw=1)
    #plt.plot(x,yp,color="blue",marker="o",lw=1,label="x^n/n")
    #plt.plot(-x,yp,color="blue",marker="o",lw=1)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=±x^n/n")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(0)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin601.gif", writer="pillow")

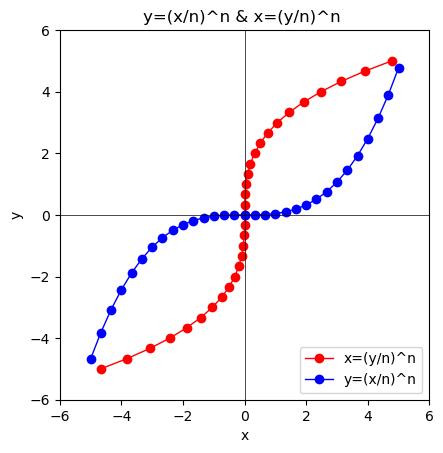
• $y=\lim_{n \to ∞}(\frac{x}{n})^n=0$あるいは$x=\lim_{n \to ∞}(\frac{y}{n})^n=0$の場合…そう、前者はy=0、後者はx=0に向けて収束するのです。

①n=1の時、y=xとx=yが重なる。

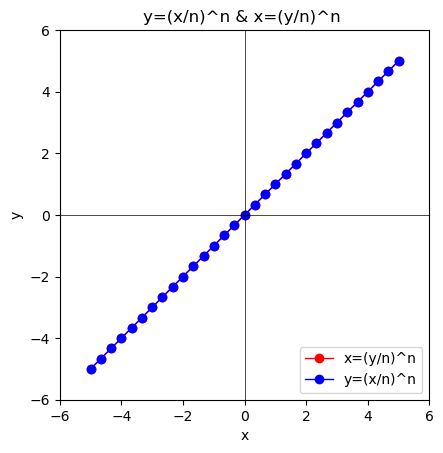
②n=2の時、偶関数系の$y=(\frac{x}{2})^2$ないしは$x=(\frac{y}{2})^2$となり、両者は座標(x,y)=(4,4)で交わる。

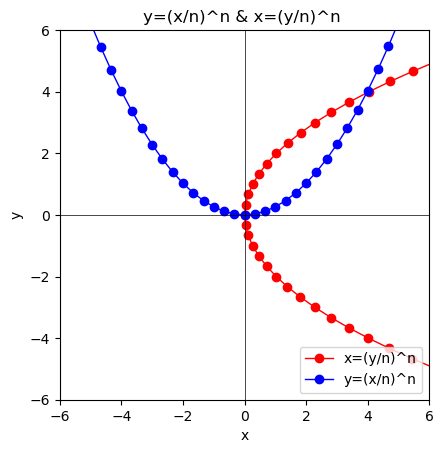
③n=3の時、奇関数系の$y=(\frac{x}{3}$)^3ないしは$x=(\frac{y}{3}^3)$となる。この調子で両者の交差座標(x,y)はどんどん無限遠点にに近づき続け、かつその値は原点から0へと近付き続ける。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#複素数
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    #c1=(-x*(1+0j))**Time_Code[n]/Time_Code[n]
    #y1=c1.real
    c2=((x*(1+0j))/Time_Code[n])**Time_Code[n]
    y2=c2.real
    #yp= np.power(x, Time_Code[n])/Time_Code[n]
    #ym=np.power(-x, Time_Code[n])/Time_Code[n]
    #yp= (np.power(abs(x), Time_Code[n]) * np.sign(x))/Time_Code[n]
    #ym= (np.power(abs(-x), Time_Code[n]) * np.sign(-x))/Time_Code[n]
    #ym= -x**Time_Code[n]/Time_Code[n]
    #描画
    plt.plot(y2,x,color="red",marker="o",lw=1,label="x=(y/n)^n")
    plt.plot(x,y2,color="blue",marker="o",lw=1,label="y=(x/n)^n")
    #plt.plot(-x,ym,color="red",marker="o",lw=1)
    #plt.plot(x,yp,color="blue",marker="o",lw=1,label="x^n/n")
    #plt.plot(-x,yp,color="blue",marker="o",lw=1)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=(x/n)^n & x=(y/n)^n ")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(4)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin102.gif", writer="pillow")

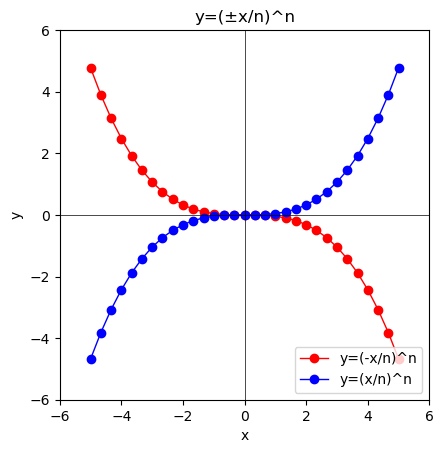
この様な形で原点に接近する様子は$y=\lim_{n \to ∞}(\frac{±x}{n})^n$の形で眺めても興味深いです。

①n=1の時はy=±xとなる。

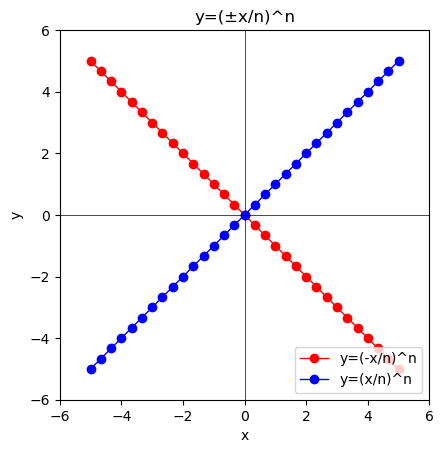
②n=2の時は偶関数$y=(\frac{±x}{2})^2$となりぴったりと重なり合う。

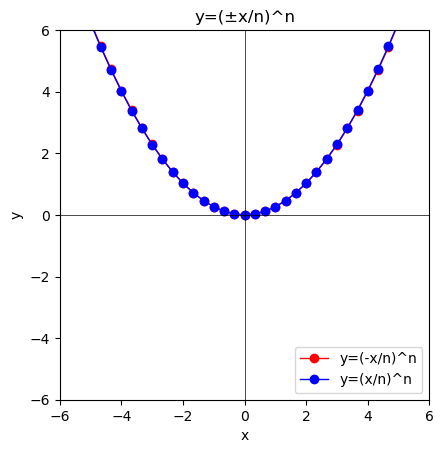
③n=3の時は奇関数$y=(\frac{±x}{3})^3$となり、この繰り返しでその値が原点から0に合流し続けていく。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#複素数
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    #c1=(-x*(1+0j))**Time_Code[n]/Time_Code[n]
    #y1=c1.real
    c2=((x*(1+0j))/Time_Code[n])**Time_Code[n]
    y2=c2.real
    #yp= np.power(x, Time_Code[n])/Time_Code[n]
    #ym=np.power(-x, Time_Code[n])/Time_Code[n]
    #yp= (np.power(abs(x), Time_Code[n]) * np.sign(x))/Time_Code[n]
    #ym= (np.power(abs(-x), Time_Code[n]) * np.sign(-x))/Time_Code[n]
    #ym= -x**Time_Code[n]/Time_Code[n]
    #描画
    plt.plot(-x,y2,color="red",marker="o",lw=1,label="y=(-x/n)^n")
    plt.plot(x,y2,color="blue",marker="o",lw=1,label="y=(x/n)^n")
    #plt.plot(-x,ym,color="red",marker="o",lw=1)
    #plt.plot(x,yp,color="blue",marker="o",lw=1,label="x^n/n")
    #plt.plot(-x,yp,color="blue",marker="o",lw=1)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=(±x/n)^n")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(4)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin203.gif", writer="pillow")

##自然指数関数(Natural Exponential Function)と自然対数関数(Natural Logarithm Function)の導入

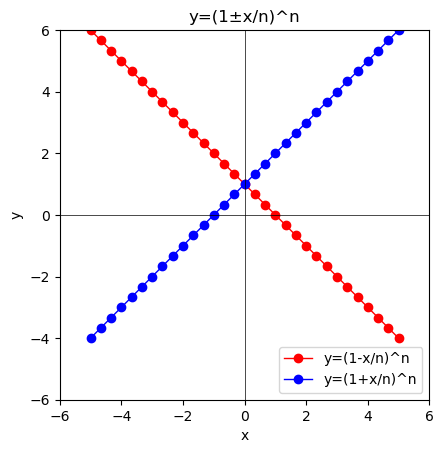
ここまで辿り着けたなら、ネイピア数exp(1)(2.718282)を求める式$y=\lim_{n \to ∞}(1+\frac{x}{n})^n$やネイピア数exp(-1)(0.3678794)を求める式$y=\lim_{n \to ∞}(1-\frac{x}{n})^n$は目前です。
【Pyrhon演算処理】同心集合①乗法的同心集合とは？

全ての指数関数(Exponential Function)$a^n$は$a^n=e^{n\log{a}}$の変換式を用いて自然指数関数(Natural Exponential Function)$e^n$へと変換可能です

その結果こに現れる曲線は自然指数関数(Natural Exponential Function)そのもの。それぞれx=1のところに現れるのがexp(1)およびexp(-1)となり、両者を掛け合わせると乗法単位元exp(0)=1となります。

①n=1の時には1次方程式y=1±xが現れる。

②n=2の時は2次方程式$y=(1+\frac{x}{2})^2$が現れる。まだまだ放物線にしか見えない。

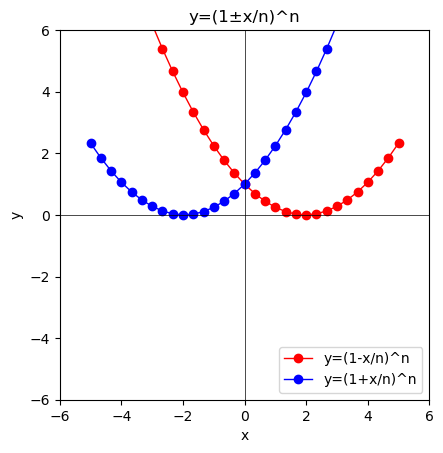
③n=3の時は3次方程式$y=(1+\frac{x}{3})^3$が現れる。おや、様子が…

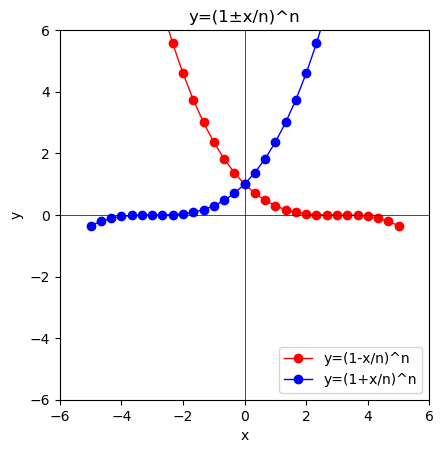
④n=4の時は4次方程式$y=(1+\frac{x}{4})^4$が現れる。随分とそれっぽく見えてきた。

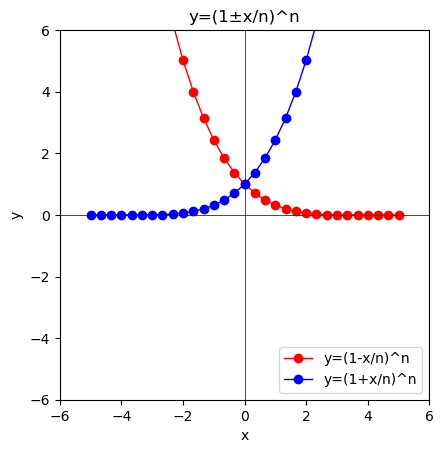
import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#複素数
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    c1=(1-(x*(1+0j))/Time_Code[n])**Time_Code[n]
    y1=c1.real
    c2=(1+(x*(1+0j))/Time_Code[n])**Time_Code[n]
    y2=c2.real
    #yp= np.power(x, Time_Code[n])/Time_Code[n]
    #ym=np.power(-x, Time_Code[n])/Time_Code[n]
    #yp= (np.power(abs(x), Time_Code[n]) * np.sign(x))/Time_Code[n]
    #ym= (np.power(abs(-x), Time_Code[n]) * np.sign(-x))/Time_Code[n]
    #ym= -x**Time_Code[n]/Time_Code[n]
    #描画
    plt.plot(x,y1,color="red",marker="o",lw=1,label="y=(1-x/n)^n")
    plt.plot(x,y2,color="blue",marker="o",lw=1,label="y=(1+x/n)^n")
    #plt.plot(-x,ym,color="red",marker="o",lw=1)
    #plt.plot(x,yp,color="blue",marker="o",lw=1,label="x^n/n")
    #plt.plot(-x,yp,color="blue",marker="o",lw=1)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=(1±x/n)^n")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(0)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin302.gif", writer="pillow")

そして指数関数$y=\lim_{n \to ∞}(1+\frac{x}{n})^n$に対して$x=\lim_{n \to ∞}(1+\frac{y}{n})^n$を考えた場合が対数関数となります。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#複素数
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def liner01(n): 
    plt.cla()
    #関数計算
    c1=(1-(x*(1+0j))/Time_Code[n])**Time_Code[n]
    y1=c1.real
    c2=(1+(x*(1+0j))/Time_Code[n])**Time_Code[n]
    y2=c2.real
    #yp= np.power(x, Time_Code[n])/Time_Code[n]
    #ym=np.power(-x, Time_Code[n])/Time_Code[n]
    #yp= (np.power(abs(x), Time_Code[n]) * np.sign(x))/Time_Code[n]
    #ym= (np.power(abs(-x), Time_Code[n]) * np.sign(-x))/Time_Code[n]
    #ym= -x**Time_Code[n]/Time_Code[n]
    #描画
    plt.plot(x,y2,color="red",marker="o",lw=1,label="y=(1+x/n)^n")
    plt.plot(y2,x,color="blue",marker="o",lw=1,label="x=(1+y/n)^n")
    #plt.plot(-x,ym,color="red",marker="o",lw=1)
    #plt.plot(x,yp,color="blue",marker="o",lw=1,label="x^n/n")
    #plt.plot(-x,yp,color="blue",marker="o",lw=1)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("y=(1+x/n)^n & x=(1+y/n)^n ")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#liner01(0)
#plt.show()

ani = animation.FuncAnimation(fig, liner01, interval=50,frames=len(Time_Code))
ani.save("lin401.gif", writer="pillow")

【初心者向け】指数・対数関数の発見とそれ以降の発展について。

	自然指数関数	自然対数関数
0	y=exp(x)	y=log(x)
1	y=exp(-x)	y=log(-x)
2	y=-exp(x)	y=-log(x)
3	y=-exp(-x)	y=-log(-x)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["y=exp(x)","y=exp(-x)","y=-exp(x)","y=-exp(-x)"],
    ["y=log(x)","y=log(-x)","y=-log(x)","y=-log(-x)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['自然指数関数', '自然対数関数'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

【初心者向け】自然指数関数と自然対数関数の交点について。

#実数冪(Real Exponentiation)と虚数冪(Imaginal Exponentiation)の使い分け?

ここで急浮上してくるのが自然指数関数/自然対数関数には「実冪系」か「虚冪系」によって振る舞いがかなり変わってくるという問題。

##虚数冪(Imaginal Exponentiation)の世界

なんだかんだいってオイラーの公式(Eulerian Formula)$e^{iθ}=cos(θ)+sin(θ)i$が著名なせいで、こちらの方が断然代表格と認識されているのです。それで三角関数とセットで用いられる「回転関数」というイメージがすっかり定着してしまいました。

【Python演算】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」？

三角関数の微分（それぞれが+90度の変遷に対応）

\cos(θ)\frac{d^n}{dθ^n}=(-\sin(θ),-\cos(θ),\sin(θ),\cos(θ),…)\\
\sin(θ)\frac{d^n}{dθ^n}=(\cos(θ),-\sin(θ),-\cos(θ),\sin(θ),…)

三角関数の積分（それぞれが-90度の変遷に対応）

\int \int \int … \int \cos(θ)(dθ)=(\sin(θ),-\cos(θ),-\sin(θ),\cos(θ),…)\\
\int \int \int … \int \sin(θ)(dθ)=(-\cos(θ),-\sin(θ),\cos(θ),\sin(θ),…)

【Python演算処理】等速円運動についての物理学と数学の立場の違い?

• $\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}$
• $\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}$

• $e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log ix),-e^{ix},-i e^{i x}(\log ix),e^{ix},…)$
• $\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log ix),- e^{i x},i e^{i x}(-\log ix),e^{ix},…)$

まぁこの全部が虚冪の説明という有様…

##実数冪(Real Exponentiation)の世界

統計学(Statistics)の分野では「平均0を中心に-∞から+∞の範囲に広がる総面積1の分布」、機械学習(Machine Learning)分野では神経エミュレーションの中核たる「0と1の間を滑らかにつなぐ曲線」を生成するのに使われていたりします。人類文明への貢献度、決して低くはないですよね？

###正規分布(Normal Distribution)
【初心者向け】正規分布(Normal Distribution)とは何か？

{\displaystyle f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\quad (x\in \mathbb {R} )}

ここではその中枢部たる$e^{-x^2}$の部分の再現のみに集中するものとします。

\lim_{n \to ∞} \int_{x=-∞}^{+∞} ±(1 \pm \frac{-x^2}{n})^n

①N=1の時$y=±(1-x^2)。正負のグラフの交点は自明の場合(Trival Case)として(1,0)(-1,0)となる。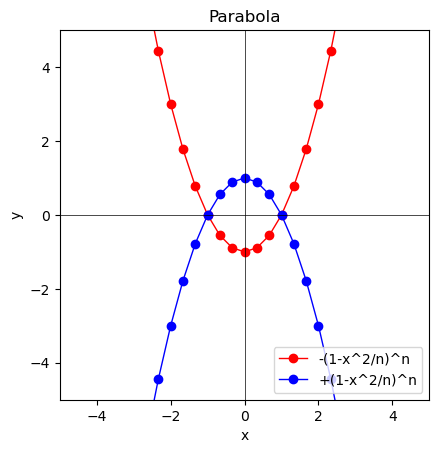

②N=2の時$±(1-\frac{x^2}{2})^2$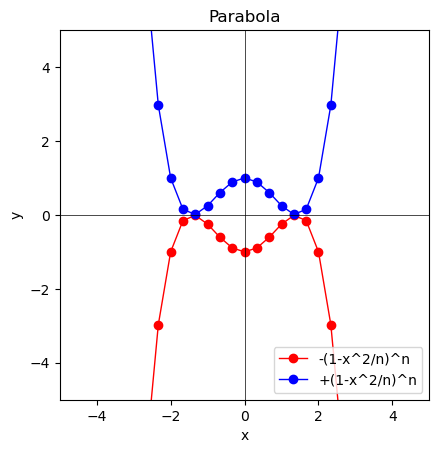

④N=3の時$±(1-\frac{x^2}{3})^3$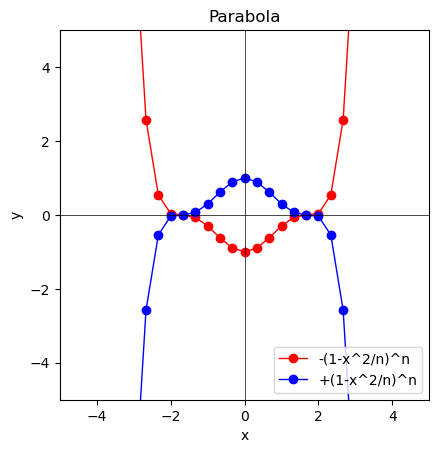

⑤以降はこの繰り返しで裾野が-∞および+∞に向けてひたすら拡張し続ける。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#放物線x
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def parabola01(n): 
    plt.cla()
    #関数計算
    y= (1+(-x**2)/Time_Code[n])**Time_Code[n]
    #描画
    plt.plot(x,-y,color="red",marker="o",lw=1,label="-(1-x^2/n)^n")
    plt.plot(x,y,color="blue",marker="o",lw=1,label="+(1-x^2/n)^n")
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-5,5])
    plt.ylim([-5,5])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("Parabola")
    ax.legend(loc='lower right')
    
Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14]

#parabola01(0)
#plt.show()

ani = animation.FuncAnimation(fig, parabola01, interval=100,frames=len(Time_Code))
ani.save("parabola06.gif", writer="pillow")

###シグモイド関数（Sigmoid Function）
シグモイド関数 - Wikipedia

{\displaystyle \varsigma _{a}(x)={\frac {1}{1+e^{-ax}}}={\frac {\tanh(ax/2)+1}{2}}}

ここでは簡略化の為に狭義のシグモイド関数、すなわちゲインを1とした標準シグモイド関数(Standard Sigmoid Function)の再現のみに集中するものとします。

\lim_{n \to ∞} \int_{x=-∞}^{+∞} \frac{1}{1+(1 \pm \frac{-x}{n})^n}

計算上x=-5→5と置いてみます。

\lim_{n=1 \to 16} \int_{x=-5}^{+5} \frac{1}{1+(1 \pm \frac{-x}{n})^n}

①n=1の時、1次関数$\int_{x=-5}^{+5} \frac{1}{2 \mp x}$。これは反比例関数y=1/xをX軸沿いに+2ズラした内容に他なりません。そう、この式自体は$e^0=1$の時に原点の値が丁度$\frac{1}{2}$を通る様に調整されているのです。

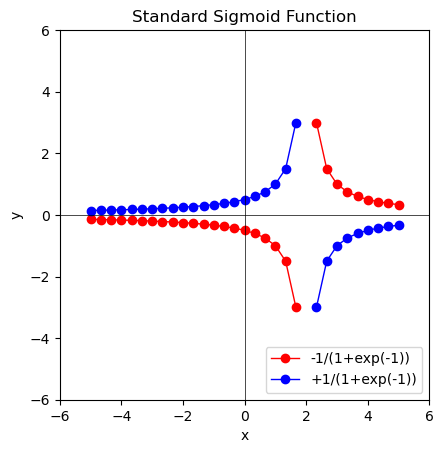
②n=2の時、2次関数$\int_{x=-5}^{+5} \frac{1}{2 \mp x^2/4}$　となります。まだまだ放物線の面影が著しいですね。

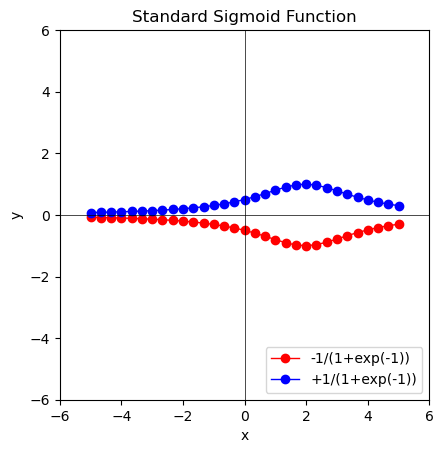
③n=3の時、3次関数$\int_{x=-5}^{+5} \frac{1}{2 \mp x^3/9}$。おや、様子が…

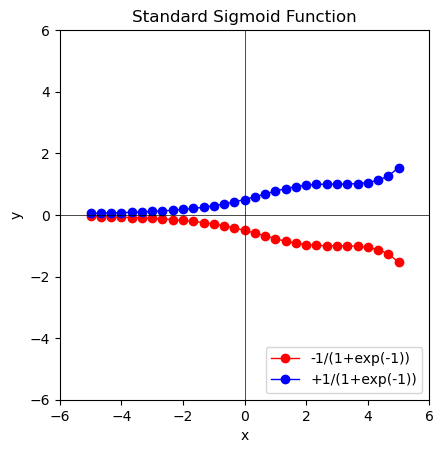
④n=4の時、、2次関数$\int_{x=-5}^{+5} \frac{1}{2 \mp x^2/4}$。大体4分割以降は安定期に入る模様。

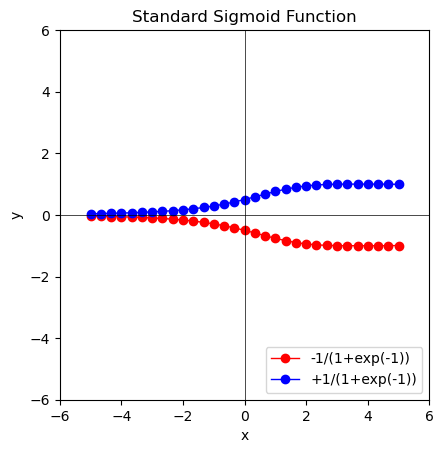
import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#放物線x
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def sigmoid01(n): 
    plt.cla()
    #関数計算
    c0=(1+(-x*(1+0j))/Time_Code[n])**Time_Code[n]
    y0=c0.real
    y=1/(1+y0)
    #描画
    plt.plot(x,-y,color="red",marker="o",lw=1,label="-1/(1+exp(-1))")
    plt.plot(x,y,color="blue",marker="o",lw=1,label="+1/(1+exp(-1))")
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-6,6])
    plt.ylim([-6,6])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("Standard Sigmoid Function")
    ax.legend(loc='lower right')

#Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]
Time_Code=np.linspace(1,16,32,endpoint = True)

#sigmoid01(0)
#plt.show()

ani = animation.FuncAnimation(fig, sigmoid01, interval=50,frames=len(Time_Code))
ani.save("sig804.gif", writer="pillow")

全体としてネイピア数計算の精度が上がれば上がるほど「有効な曲線の端」が伸びていく印象。同じ傾向は虚冪の場合にも見て取れます。
【Rで球面幾何学】「世界で一番美しい公式」オイラーの等式の罠？

そんな感じで、以下続報…