【初心者向け】自然指数関数(Natural Exponential Function)と自然対数関数(Natural Logarithmic Function)の交点について。

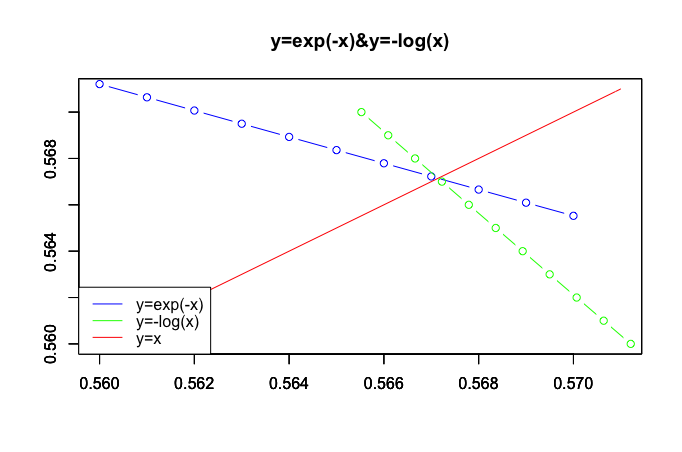
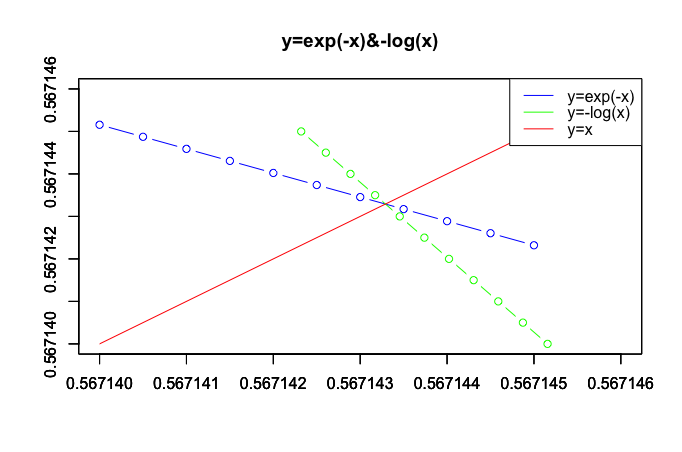
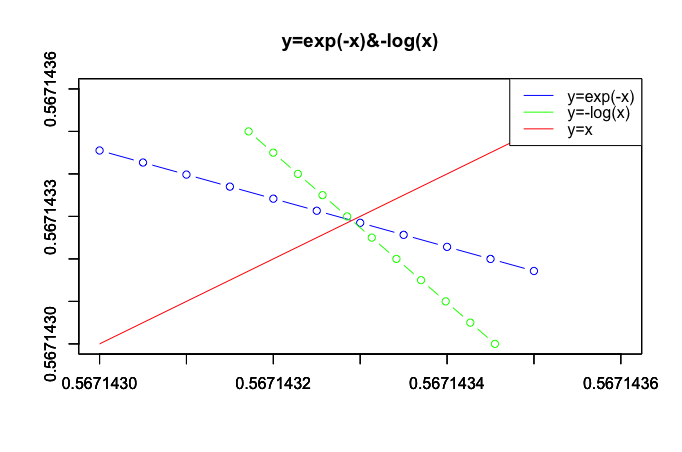
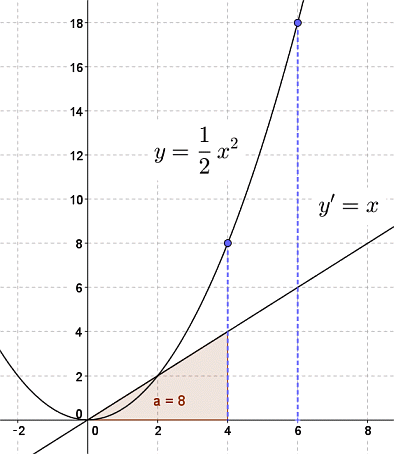
以前の投稿でこんな図を作成しました。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。

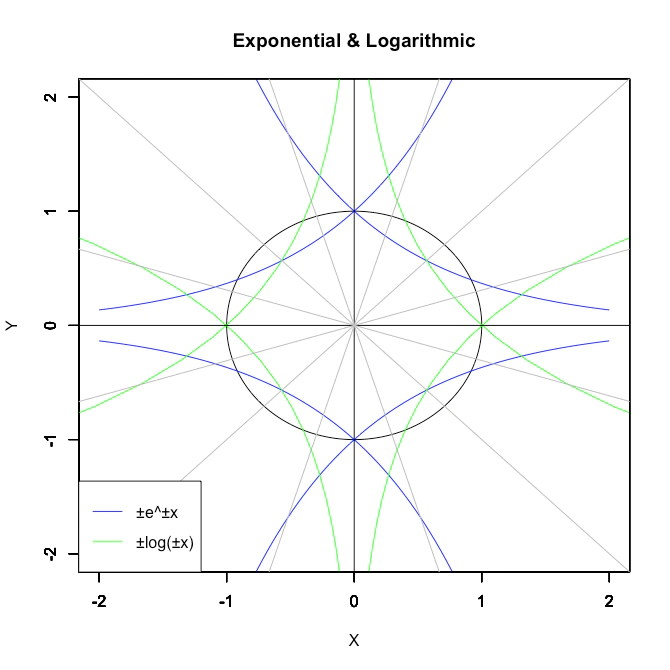
ここで気になるのが自然指数関数(Natural Exponential Function)と自然対数関数(Natural Logarithmic Function)の交点α。全部で{α,α}{-α,α}{α,-α}{-α,-α}と4個ありますが{α,α}の場合を調べれば、残りは自明の場合(Trival Case)として定まります。

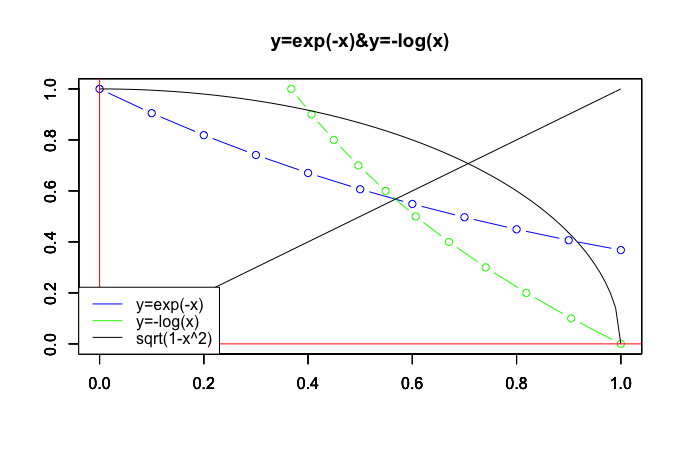
統計原義Rでの検証例

min<-0
max<-1
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
crc<-function(x)sqrt(1-x^2)
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max),ylim=c(min,max),main="y=exp(-x)&y=-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max),ylim=c(min,max),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(crc,type="l",xlim=c(min,max),ylim=c(min,max),main="",xlab="",ylab="")

par(new=T) 

plot(lf,type="l",xlim=c(min,max),ylim=c(min,max),main="",xlab="",ylab="")
abline(v=0,col=rgb(1,0,0))
abline(h=0,col=rgb(1,0,0))
legend("bottomleft", legend=c("y=exp(-x)","y=-log(x)",y="sqrt(1-x^2)"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))

#exp(-x)の範囲は0.5と0.6の間
> cex[6:7]
[1] 0.5 0.6

#log(exp(-1))の範囲は0.5488116と0.6065307の間
> clx[6:7]
[1] 0.6065307 0.5488116

観測精度(Observation Accuracy)をもう一桁引き上げてみましょう。

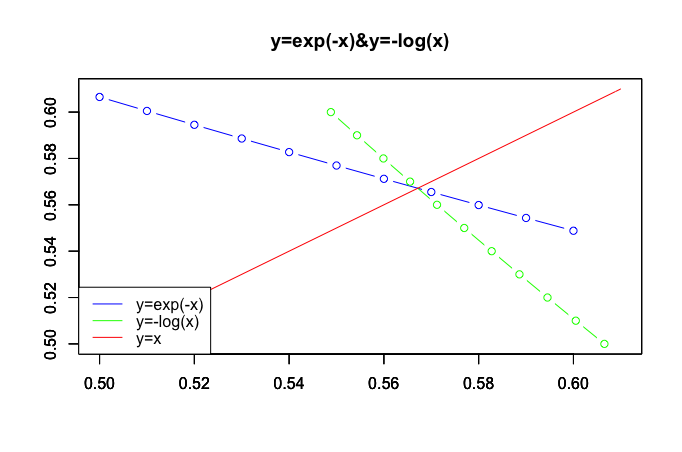
統計原義Rでの検証例

unit<-0.01
min<-0.5
max<-0.6
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="y=exp(-x)&y=-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(lf,type="l",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("bottomleft", legend=c("y=exp(-x)","y=-log(x)","y=x"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

#exp(-x)の範囲は0.56と0.57の間
> cex[7:8]
[1] 0.56 0.57
#log(exp(-1))の範囲は0.5769498と0.5827483の間
> clx[5:6]
[1] 0.5827483 0.5769498

さらにもう一桁。

統計原義Rでの検証例

unit<-0.001
min<-0.56
max<-0.57
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="y=exp(-x)&y=-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(lf,type="l",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("bottomleft", legend=c("y=exp(-x)","y=-log(x)","y=x"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

#exp(-x)の範囲は0.566と0.567の間
> cex[8:7]
[1] 0.567 0.566

> exp(-0.566)
[1] 0.5677921
> exp(-0.567)
[1] 0.5672246
#log(exp(-1))の範囲は0.5689288と 0.5694980の間
> clx[3:4]
[1] 0.5700678 0.5694980
> log(exp(-0.566))
[1] -0.566
> log(exp(-0.567))
[1] -0.567

さらにもう一桁…おや、接していない!?

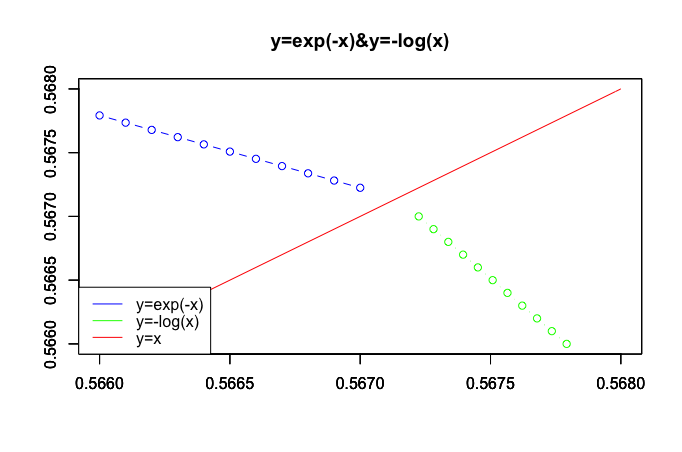
統計原義Rでの検証例

unit<-0.001
min<-0.566
max<-0.567
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="y=exp(-x)&y=-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(lf,type="l",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("bottomleft", legend=c("y=exp(-x)","y=-log(x)","y=x"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

どうしてそんな展開に…よく分からないまま、グラフに導かれるまま観測範囲を0.5670-0.5675に切り替えてみます。ついでに凡例の位置も左下から右上に変更。

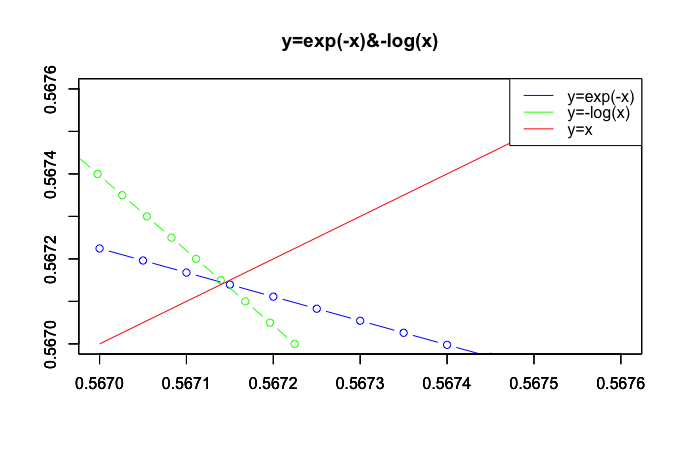
統計原義Rでの検証例

unit<-0.0001
min<-0.5670
max<-0.5675
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="y=exp(-x)&-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(lf,type="l",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("topright", legend=c("y=exp(-x)","y=-log(x)","y=x"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

#exp(-x)の範囲は0.56710と0.56715の間
> cex[3:4]
[1] 0.56710 0.56715
> exp(-0.5671)
[1] 0.5671678
> exp(-0.56715)
[1] 0.5671395

#log(exp(-x))の範囲は0.5670261と 0.5670544の間
> clx[7:8]
[1] 0.5670544 0.5670261
> log(0.5670544)
[1] -0.5673
> log(0.5670261)
[1] -0.5673499

さらにもう1回。以降はピッチが0.5単位に。

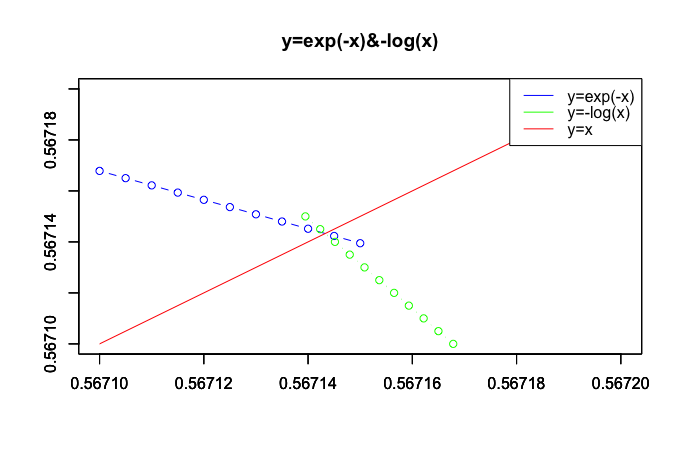
統計原義Rでの検証例

unit<-0.00005
min<-0.56710
max<-0.56715
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="y=exp(-x)&-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(lf,type="l",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("topright", legend=c("y=exp(-x)","y=-log(x)","y=x"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

#exp(-x)の範囲は0.567140と0.567145の間
> cex[9:10]
[1] 0.567140 0.567145
> exp(-0.567140)
[1] 0.5671452
> exp(-0.567145)
[1] 0.5671423

#log(exp(-x))の範囲は0.5670261と 0.5670544の間
> clx[2:3]
[1] 0.5671650 0.5671622
> log(0.5671650)
[1] -0.567105
> log(0.5671622)
[1] -0.5671099

さらにもう1回。

統計原義Rでの検証例

unit<-0.000001
min<-0.567140
max<-0.567145
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="y=exp(-x)&-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(lf,type="l",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("topright", legend=c("y=exp(-x)","y=-log(x)","y=x"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

#exp(-x)の範囲は0.5671430と0.5671435の間
> cex[7:8]
[1] 0.5671430 0.5671435
> exp(-0.5671430)
[1] 0.5671435
> exp(-0.5671435)
[1] 0.5671432

#log(exp(-x))の範囲は0.5671440と0.5671443の間
> clx[4:5]
[1] 0.5671443 0.5671440
> log(0.5671440)
[1] -0.567142
> log(0.5671443)
[1] -0.5671415

さらにもう1回。

統計原義Rでの検証例

unit<-0.0000001
min<-0.5671430
max<-0.5671435
cx<-seq(min,max,length=11)
f0<-function(x)exp(-x)
cy<-f0(cx)
cex<-cx
cey<-cy
clx<-cy
cly<-cx
lf<-function(x)x

plot(cex,cey,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="y=exp(-x)&-log(x)",xlab="",ylab="",col=rgb(0,0,1))

par(new=T) 

plot(clx,cly,type="b",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(0,1,0))

par(new=T) 

plot(lf,type="l",xlim=c(min,max+unit),ylim=c(min,max+unit),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("topright", legend=c("y=exp(-x)","y=-log(x)","y=x"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

#exp(-x)の範囲は0.5671432と0.5671433の間
> cex[6:7]
[1] 0.5671432 0.5671433
> exp(-0.5671432)
[1] 0.5671433
> exp(-0.5671433)
[1] 0.5671433

#log(exp(-x))の範囲は0.5671433
> clx[5:6]
[1] 0.5671433 0.5671433
> log(0.5671433)
[1] -0.5671433

どうやら0.5671433が手持ち環境で到達可能な精度での極限となる模様。この数字にどんな意味があるか、早速ネットで検索してみましょう。
newtonsys function | R Documentation
ああ何という事でしょう。統計言語Rのニュートン=ラプソン法関数(Newton-Raphson Method Function) のサンプルコードくらいしか検索に引っ掛かってきません。
統計原義Rでの検証例

library(pracma)
F3 <- function(x)
c(2*x[1] - x[2] - exp(-x[1]), -x[1] + 2*x[2] - exp(-x[2]))
newtonsys(F3, c(0, 0))
# $zero 0.5671433 0.5671433
# $fnorm 0
# $niter 4

この関数自体の詳細は不明ながら、ニュートンラプソン法だと関数y=exp(-x)と関数y=-log(x)の差が0になる交点を求める形になると分かりました。
統計原義Rでの検証例

> f2<-function(x)-log(x)-exp(-x)
> uniroot(f2, c(0, 1))
$root
[1] 0.5671401
$f.root
[1] 3.821394e-06
$iter
[1] 5
$init.it
[1] NA
$estim.prec
[1] 6.103516e-05

#反復計算過程の表示
f2<-function(x){print(x);-log(x)-exp(-x)}
uniroot(f2, c(0, 1))
[1] 0
[1] 1
[1] 0.5
[1] 0.5952885
[1] 0.5691769
[1] 0.5671401
[1] 0.5672011
[1] 0.5671401

ところで…

• exp(-α)=x
• log(exp(-α))=-α=log(x)
• α=-log(x)

従って実は関数y=exp(-x)や関数y=log(exp(-x))と関数y=xの交点0を求めるのと同じ事です。

統計原義Rでの検証例

#y=exp(-x)と関数y=xの交点
f0<-function(x)exp(-x)-x
uniroot(f0, c(0, 1))
$root
[1] 0.5671439
$f.root
[1] -9.448109e-07
$iter
[1] 3
$init.it
[1] NA
$estim.prec
[1] 7.424999e-05

#反復計算過程の表示
f0<-function(x){print(x);exp(-x)-x}
uniroot(f0, c(0, 1))
[1] 0
[1] 1
[1] 0.6126998
[1] 0.5670696
[1] 0.5671439
[1] 0.5671439

#関数y=-log(x)と関数y=xの交点

f1<-function(x)-log(x)-x
uniroot(f1, c(0, 1))
$root
[1] 0.5671433
$f.root
[1] -3.262866e-08
$iter
[1] 5
$init.it
[1] NA
$estim.prec
[1] 6.103516e-05

#反復計算過程の表示
f1<-function(x){print(x);-log(x)-x}
uniroot(f1, c(0, 1))
[1] 0
[1] 1
[1] 0.5
[1] 0.5809402
[1] 0.5676828
[1] 0.5671433
[1] 0.5670823
[1] 0.5671433

そもそもニュートン・ラフソン法（Newton-Raphson method）とはどういう方法論なのでしょう？
ニュートン法 - Wikipedia

f(x)=0となるxを求める場合、xの付近に適当な値X0をとり、次の漸化式によってxに収束する数列Xnが得られる場合が多い。

X(n+1)=Xn-f(Xn)/'f(Xn)

関数f(x)を微分した結果得られる導関数(Derivative Function)'f(x)が登場してくるという事は、ニュートンラプソン法の概念理解には微分(Differential)の知識が必須という事です。
導関数の意味といろいろな例
というより、ある意味ここに出てくる考え方こそが微分概念そのもの？

【積分】原始関数と導関数の関係

導関数がＸ軸とY軸の間に間に作る面積は原始関数の値と一致する。

落下運動
運動エネルギーの基本式

自由落下運動(Free Fall Movement)とは以下の様な運動を指す。
①重力加速度0.98(=:1,単位m/s^2)の力のかかる向きが進行方向と完全に一致する。
②初速0(m/s)で時間t=0(s)の時の位置y=0(m)とする。
この時、
①時間t=x(s)時点の速度v=gt(m/s)となる。

②時間t=x(s)時点の位置y=1/2×gt^2(m)となる。

③1/2なる数字は(三角形の面積(h(高さ)+v(幅))/2を求める要領で)時間t=0時点の速度v=0(m/s)から時間x(s)時点までの速度v=gt(m/s)までの平均速度(m/s)を求める過程で現れる。
従ってv^2=2gyが成立。

このv^2=2gyこそが微積分概念(Calculus Concept)の根幹であり、半径rの円(円周長2πr)の面積がπr^2で求められる事とも密接に関わってくる訳ですね。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

統計原義Rでの検証例

#例えばsqrt(2)を求める計算。
#関数y=x^2とy=2の交点0を求める計算はこうなる。
#x^2-2=0
#再帰演算で考える場合、まずこれを微分する。
> f0<-expression(x^2-2) 
> D(f0,"x")
2 * x

#そしてx-(x^2-2)/2x=(x+2/x)/2
nr01<-function(x)(x+2/x)/2
>nr01(1)
[1] 1.5
> nr01(1.5)
[1] 1.416667
> nr01(1.416667)
[1] 1.414216
> nr01(1.414216)
[1] 1.414214
> nr01(1.414214)
[1] 1.414214

#uniroot関数の演算結果
f1<-function(x){print(x);x^2-2}
uniroot(f1, c(1, 2))
$root
[1] 1.414213
$f.root
[1] -6.855473e-07
$iter
[1] 5
$init.it
[1] NA
$estim.prec
[1] 6.103516e-05

[1] 1
[1] 2
[1] 1.333333
[1] 1.419048
[1] 1.414072
[1] 1.414213
[1] 1.414274
[1] 1.414213

exp(-x)-xと置いた場合の解き方。
統計原義Rでの検証例

#まず関数exp(-x)-xを微分する。
> f1<-expression(exp(-x)-x) 
> D(f1,"x")
-(exp(-x)+1)

#この式を'f(x)に代入。
nr02<-function(x){x-(exp(-x)-x)/(-(exp(-x)+1))}

> nr02(0)
[1] 0.5
> nr02(0.5)
[1] 0.566311
nr02(0.566311)
> nr02(0.566311)
[1] 0.5671432
> nr02(0.5671432)
[1] 0.5671433
> nr02(0.5671433)
[1] 0.5671433

-log(x)-x=0と置いた場合の解き方。
統計原義Rでの検証例

#まず関数-log(x)-xを微分する。
> f2<-expression(-log(x)-x) 
> D(f2,"x")
-(1/x + 1)

#この式を'f(x)に代入。
nr03<-function(x){x-(-log(x)-x)/(-(1/x + 1))}

#0は代入出来ないので0.1より出発。
> nr03(0.1)
[1] 0.300235
> nr03(0.300235)
[1] 0.5087347
> nr03(0.5087347)
[1] 0.5650776
> nr03(0.5650776)
[1] 0.5671409
> nr03(0.5671409)
[1] 0.5671433
nr03(0.5671433)
> nr03(0.5671433)
[1] 0.5671433

-log(x)-exp(-x)=0と置いた場合の解き方。
統計原義Rでの検証例

#まず関数-log(x)-exp(-x)を微分する。
> f3<-expression(-log(x)-exp(-x)) 
> D(f3,"x")
-(1/x - exp(-x))

#この式を'f(x)に代入。
nr04<-function(x){x-(-log(x)-exp(-x))/(-(1/x - exp(-x)))}

#0は代入出来ないので0.1より出発。
> nr04(0.1)
[1] 0.2536803
> nr04(0.2536803)
[1] 0.4418468
> nr04(0.4418468)
[1] 0.5491944
> nr04(0.5491944)
[1] 0.5667973
> nr04(0.5667973)
[1] 0.5671432
> nr04(0.5671432)
[1] 0.5671433
nr04(0.5671433)
> nr04(0.5671433)
[1] 0.5671433

どう計算しても答えは概ね0.5671433。ところで肝心の疑問の答えが得られてません。この数にどんな意味が？　
指数関数と対数関数の交わる点
無限べき乗a^a^a^...の収束と発散との境目が気になる
一般に無限冪乗や指数関数と対数関数の交点の極限は1/2と考えられてますが、それとはズレてるんですね。