(2021年4月03日)投稿。
(2021年4月12日)回転方向を反時計回りで統一。
【数理考古学】冪乗算(Exponentiation)の微積分
冪乗算(Exponentiation)の微積分定理は以下となります。
- $\frac{1}{β+1}x^{β+1}$を微分すると$x^β$となる。
- $x^β$を積分すると$\frac{1}{β+1}x^{β+1}+C$となる(不定積分)。
- ただしβ=-1の時は分母が0となり計算出来ない。
等差数列(Arithmetic Sequence=算術数列)や等比数列(Geometric Sequence=幾何数列)との関係からこの現象を追っていくと以下となります。
【数理考古学】とある実数列の規定例②等比数列から乗法群へ
- 初項1、公差1の時に添字と演算結果集合が一致する等差数列は、公比1,公差0の時に公比1,公差1の等比数列と重なる(Y=1)。ラップ級数(Rap Series)$N_n(n=-\infty→0→)=(1,…,1,1,1,…,1)$を生成する演算たる1の冪乗$y=1^n$同様、Xの値によらずYの値が1に定まるのである。
【Python演算処理】単位円筒を巡る数理 - 等比数列は理論上初項0,公比0の時にy=0に到達するがコンピューターは負数の場合それをちゃんと計算しない($n\geqq0$の時は0、$n<0$の時はNaNを返す)。一方冪乗算$y=0^n$は正数$(n>0)$に対して0,0$(n=0)$に対して1、負数$(n<0)$の時に無限大$\infty$を返す。
- この反応のズレは$n\geqq0$で等比数列と冪乗算の添字が一つズレる事と密接な関係があると目される。

この様な形で現れる到達不可能地点を数学の世界では特異点(Singularity)と呼びます。
特異点 - Wikipedia
正負概念導入に伴う特異点の発生
ピタゴラスの定理$y=±\sqrt{1-x^2}$も半円ずつしか描けません($Y=0$の場合が特異点)。$x=±\sqrt{1-y^2}$も同様($x=0$の場合が特異点)。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?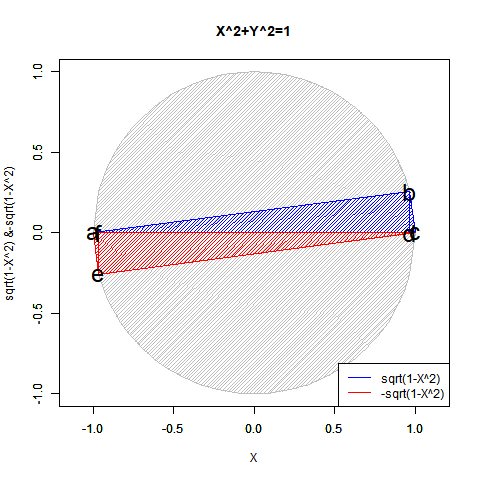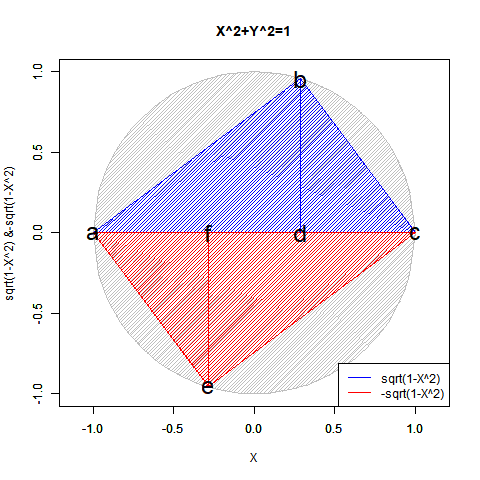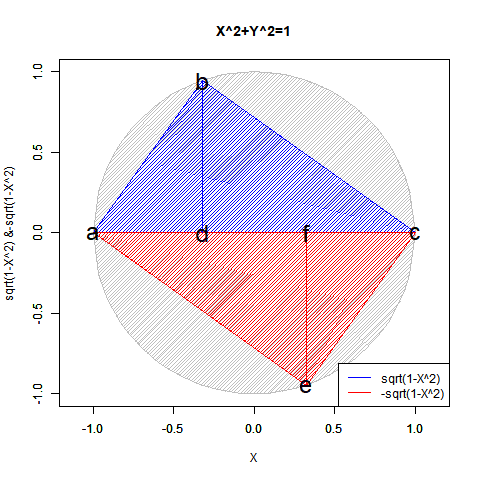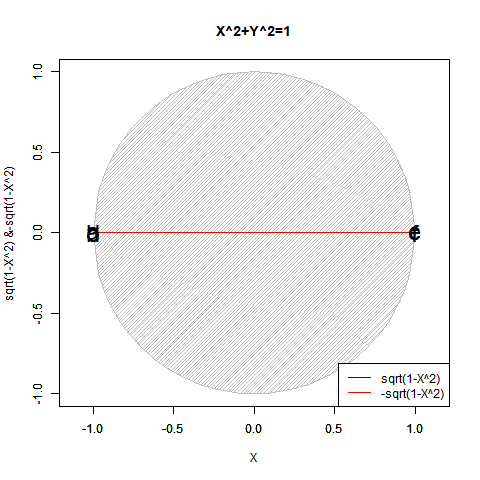
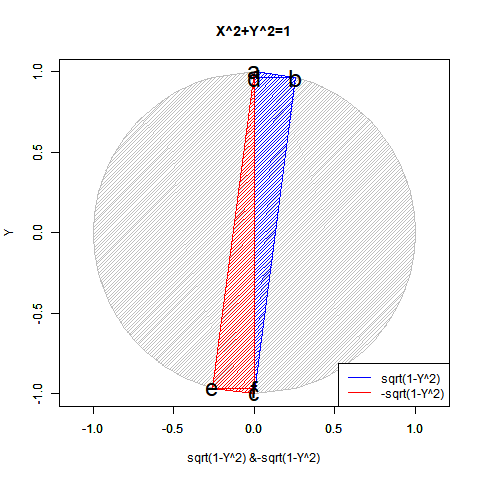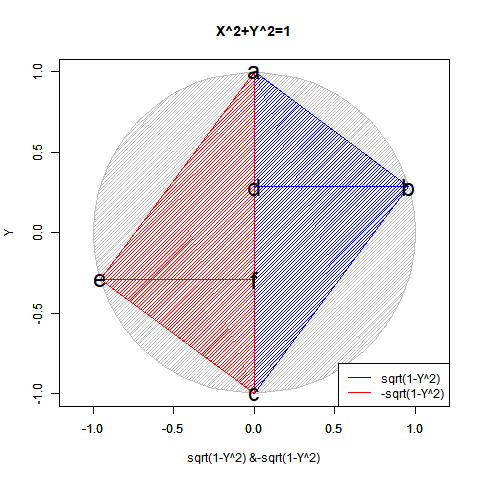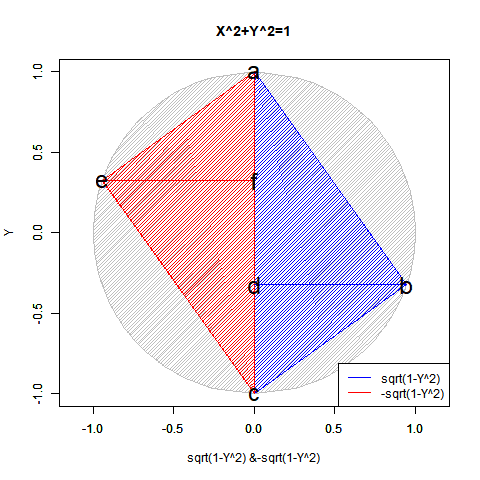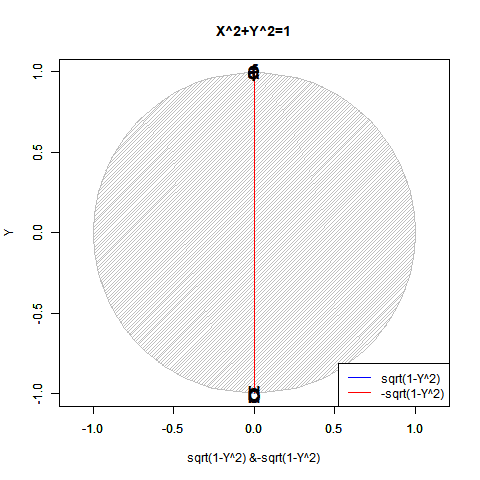
かかる特異点は「正負の概念導入に伴う円弧概念の二分」に由来し、偶奇性(Parity)や「対蹠間を結ぶ円弧状に2つ、球表面上には無数に存在する経路」複素共益(Complex Conjugate)の概念と同時発生する訳です。
【Python演算処理】単位円筒を巡る数理


【初心者向け】複素共役のアニメーション表示について。
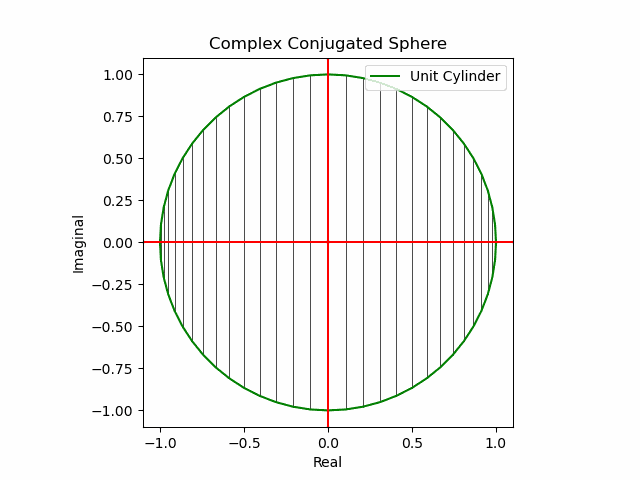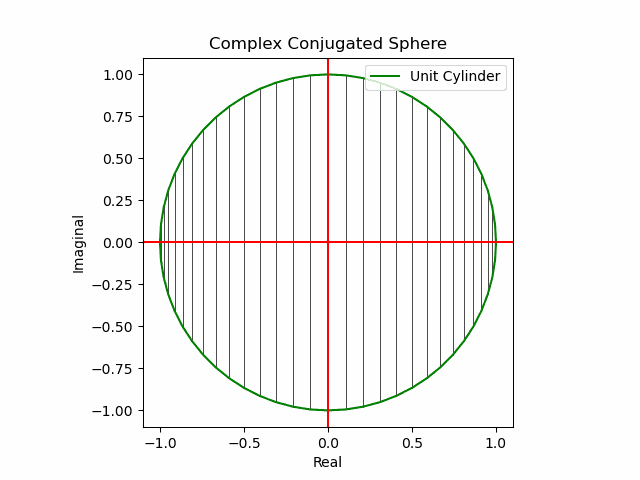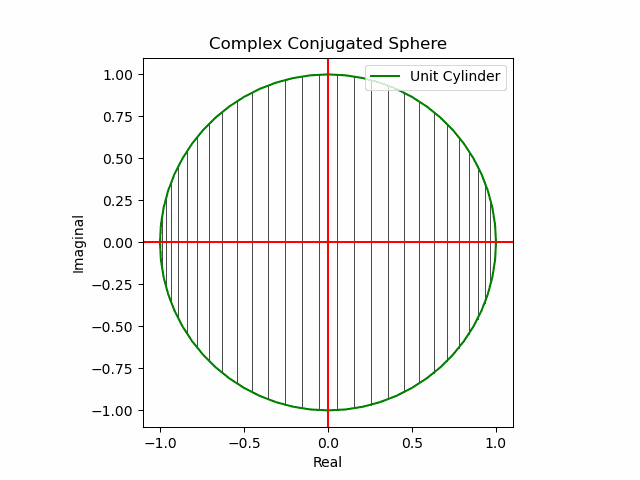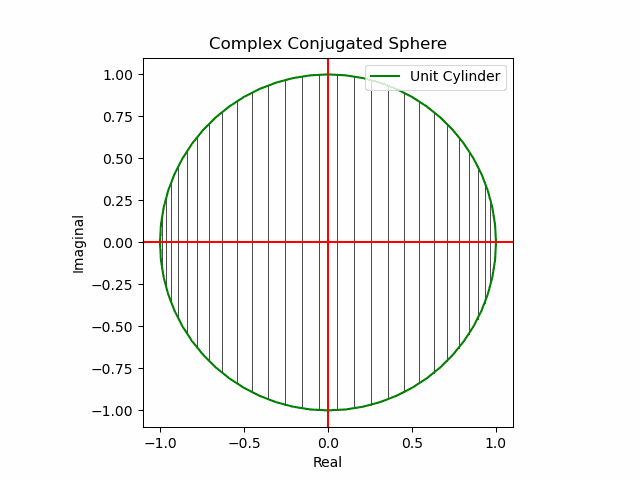
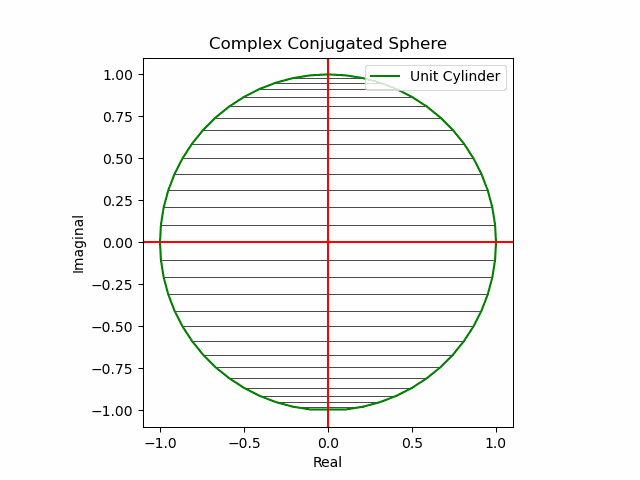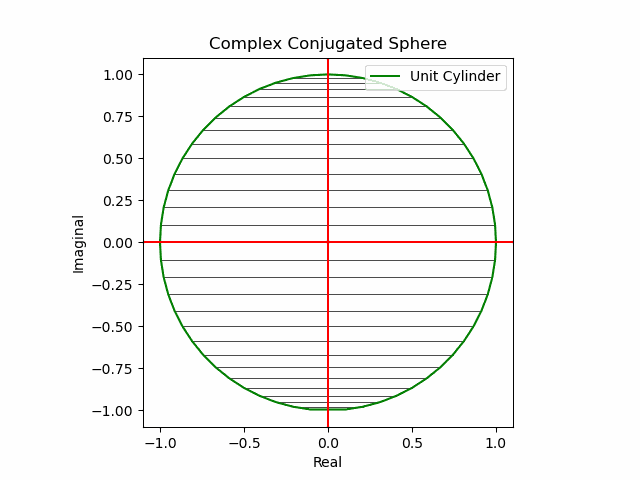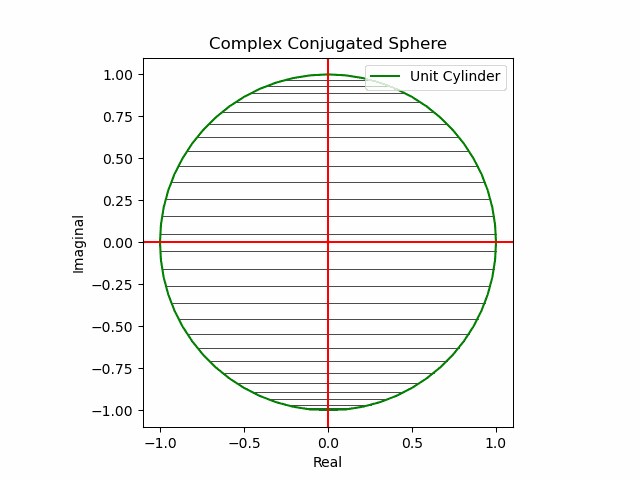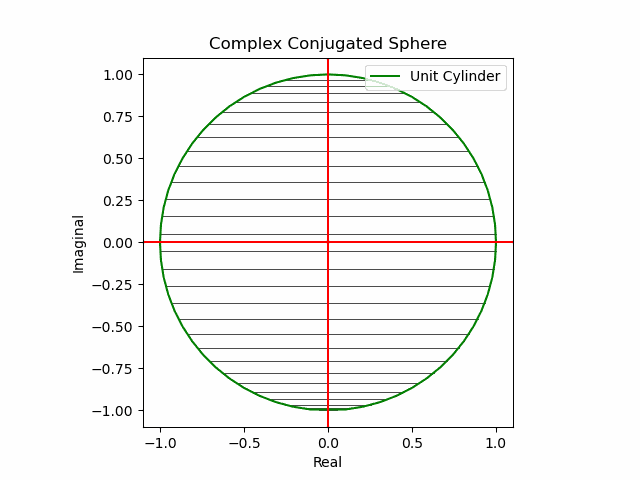
【Python演算処理】単位円筒(Unit Cylinder)を巡る数理


まさしく「騙し絵版画家」エッシャー(Maurits Cornelis Escher, 1898年~1972年)「版画画廊(Print Gallery,1956年)」における中央空白部のイメージ。
エッシャーはどのようにして「奇想の版画家」になったのか?
『版画の画廊』における「ミーズ・アン・ナビーム」

エッシャーの騙し絵については以前「正四面体の空間充填性(単独では備えず、正八面体と組み合わせる必要がある)」でも触れました。人間の空間認識能力はかくも騙されやすいのです。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

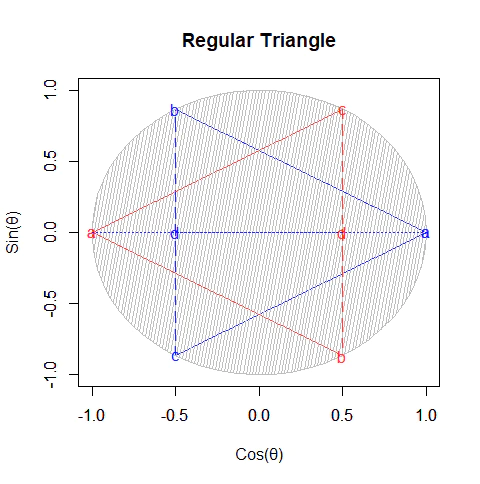




上掲の複素共益アニメーションが観察者の認識によって進行方向を変える様に(カンブリア爆発期以降一部の生物が備える様になった視覚とその情報を処理する脊髄に由来する)人間の空間認識能力(およびその発展形たる数理処理能力)は欠陥だらけ。おそらく負数や虚数の概念はそれを補う為に発明されたと考えるべきなのです。
物理学における等速円運動の解釈
等速円運動についての物理学と数学の立場の違い?
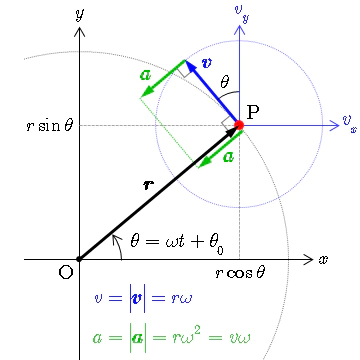
物理学の世界は等速円運動を円軌道上の直線運動として捉え様としますが、この考え方だけでは「X方向に1進もうとしてY方向にも1進んでしまう過程において移動距離が伸びる」主観的体験を説明し尽くす事が出来ません。移動距離に注目するなら等速円運動は1動くのに$\frac{π}{2}$、2動くのにπ進まねばならない運動でもある訳で、それがどういう条件でどれだけズレるか数理的に明らかにするのが距離関数(Metric Function)の課題設定。この場合は曲率が0の場合、あるいは+∞の場合が特異点として追加される事になります。
【初心者向け】方形描画関数②距離空間との関係。
おや、特異点が増えてしまいました!! かかる状況を説明する為、座標系における視界(Visibility)なる概念を導入したいと思います。
- 実軸が1本も設定されてない時、視界は片側無限数列(One-sided Infinite Sequence)で表現可能な範囲で無制限と映る。平面状極座標系(Planar Polar Coordinates System=二次元)では…
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
同じく片側無限数列に立脚する球状極座標系(Spheroidal Polar Coordinates System=三次元)では…
【初心者向け】「単位円筒」から「単位球面」へ
ただし両側無限数列(Both-sided Infinite Sequence)に立脚する円柱状極座標系(Cylindrical Polar Coordinates System=三次元)は、この段階では以下の不完全な形でしか表現し得ない。
【Python演算処理】単位円筒(Unit Cylinder)を巡る数理
- 正負の概念を導入すると(実軸を1本だけ導入すると)、今度は平面状極座標系上において半円しか描けなくなる。視界$\frac{1}{2}$(x=1→-1,y=0→±1)のy=±$\sqrt{1-x^2}$と同じく視界$\frac{1}{2}$(x=0→±1,y=-1→1)のx=±$\sqrt{1-y^2}$の対称式一対…
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ

かかる制限を撤廃すべく、複素平面(Complex Plane)はこれらの対称式をそれぞれ$\cos(θ)+\sin(θ)i$(初期位相0ラジアン,反時計回り)と$\sin(θ)+\cos(θ)i$(初期位相π/2ラジアン,時計回り)と表す様になった訳である。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ

一方、円柱状極座標系はやっと完全な形で表現可能となるが…
【Python演算処理】単位円筒(Unit Cylinder)を巡る数理
複素平面上での判断の反映させ方に(分枝切断点を1つだけ置いて)周期を1に取る方法と(分枝切断点を2つ置いて)2に取る方法の2通りがあり、後者を選ぶと偶奇の概念が導入される。
【Python演算処理】単位円筒(Unit Cylinder)を巡る数理



こうした考え方の延長線上において実数軸を2本導入する方法は2通りあります。
- いわゆるデカルト座標系(Cartesian Coordinate System)をそのまま単純に導入し、横軸(X軸)の視界$\frac{1}{2}$と縦軸(Y軸)の視界$\frac{1}{2}$を合算すると$\frac{3}{4}$となってしまうので、全体像を視界$\frac{3}{4}(-i→-(i^2)=1→-(-i)=i)$の実軸(Real Axis)と虚軸(Imaginal Axis)の交代と捉えて「死角」を封じたのが複素数表現となる。それ自体は実軸を1本導入しただけの一次元表現である点に注意。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?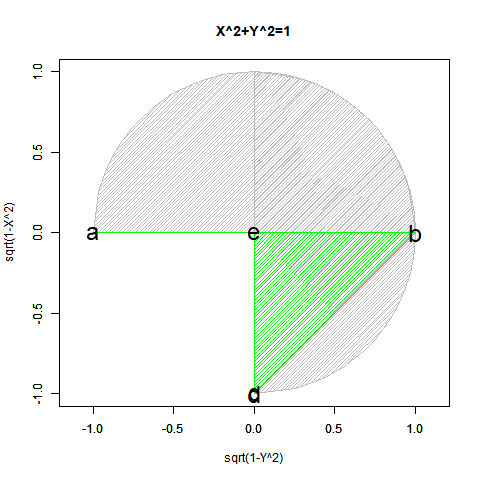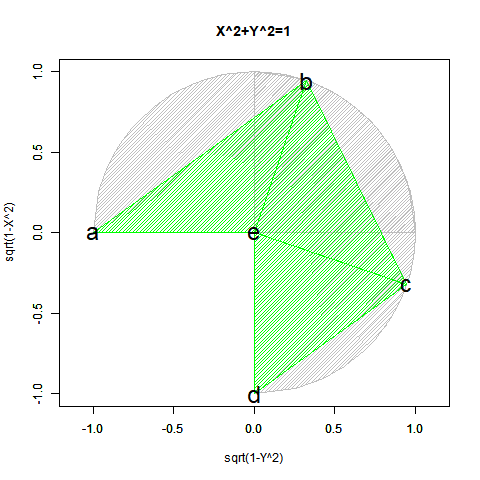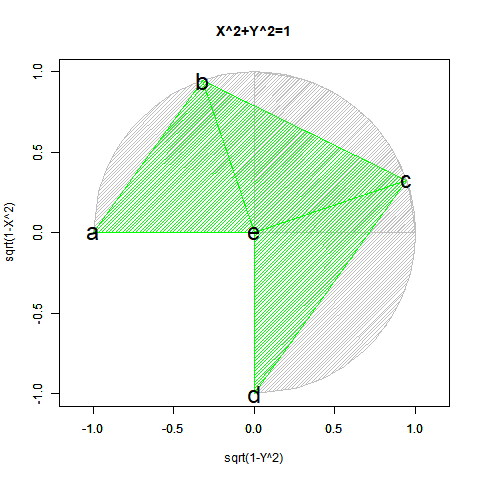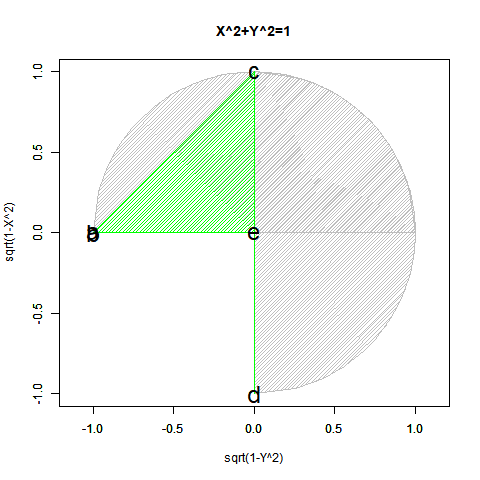
ところで、実軸を2本導入した時点で$\frac{1}{4}$となる「死角」は理論上、導入する実軸を無限に増やし続ける事で限りなく0ラジアンに近づけていける(それに応じて視界は全周=2πラジアンに接近する)が、これを求めるベルヌーイ試行「N回の試行で確率p/Nの事象が1度も起らない確率」の計算式$(1-\frac{1}{n})^n$は、実は$e^{-1}$(ネイピア数の逆数)を求める計算式そのものなのである。その事を式で表したのがオイラーの等式$e^{πi}=(1±\frac{πi}{N})^N=(0±1i)^{2x}=-1$となり、共益複素数(Conjugate Complex Number)が「1から-1に向かう(平面上は2つ、球表面上には無数にある)経路」として把握される展開を迎える。
ベルヌーイ試行 - Wikipedia
【初心者向け】指数・対数関数の発見とそれ以降の発展について。
そして特異点に到達不可能だという事は、視界が常に開空間としてのみ存在する(すなわち観測結果集合も開集合としてのみ存在する)事を意味します。
近傍 (位相空間論) - Wikipedia
Γ関数の登場
ところで円の面積を求める公式$πr^2$を半径rで微分すると円周を求める公式$2πr$になりますが、πを変数に見立て、これで微分すると$\frac{\sqrt{π}}{2}r^2$となります。そしてこの見慣れない$\frac{\sqrt{π}}{2}$なる数字、Γ関数に1/2(すなわち1と2の中間値)を与えた場合の返り値としても登場してくるのです。
【Python演算処理】階乗と順列と組み合わせ

import numpy as num
from scipy.special import gamma
# [Γ(1) Γ(1.5) Γ(2)]
a=gamma([1, 1.5, 2])
a=num.round(a, 8)
print("Γ(1,1.5,2)=",a)
# sqrt(π)/2
b=num.sqrt(num.pi)/2
b=num.round(b, 8)
print("sqrt(π)/2=",b)
# 出力結果
Γ(1,1.5,2)= [1. 0.88622693 1. ]
sqrt(π)/2= 0.88622693
- 階乗計算を小数点下の添字にも対応させたΓ関数はガウス関数$e^{-x^2}$を実数域全体で広義積分したガウス積分(Gaussian integral)$\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{π}$と密接な関係がある。
- 被積分関数が偶関数なので$\int_{-\infty}^{\infty}e^{-x^2}dx=2\int_{0}^{\infty }e^{-x^2}dx$が成立。計算が単純化される。
- ここで変数変換$x=t^{\frac{1}{2}}$を行えばオイラー積分が可能となり、半整数値の階乗が$\sqrt{π}$の有理数倍となる事が示される。
2\int_{0}^{\infty }e^{-x^2}dx=2\int_{0}^{\infty }\frac{1}{2}e^{-t}t^{\frac{1}{2}}dt=2Γ(\frac{1}{2})=\sqrt{π}
- これを一般すれば$\int_{0}^{\infty }e^{-ax^b}dx=\frac{1}{b}a^{\frac{-1}{b}}Γ(\frac{1}{b})$となる。
このΓ関数の概念を用いると円概念、すなわち半径/直径/円弧/球面/体積それぞれの計算式の往復をスッキリ一つの体系に統合する事が出来ます。
【Python演算処理】「N次球概念導入による円/球関係の数理の統合」?
かかる円概念統合において「円弧と面積の計算式の往復」や「球面と体積の計算式の往復」と関連してくるので、重積分を用いた証明も示しておきましょう。
Pythonで数学の勉強:微分積分学
- 半球D、すなわち$z=\sqrt{1-x^2-y^2}$と$z=0$に囲まれた部分の体積Vを求める。
v=\iint_{D}\sqrt{1-x^2-y^2}dxdy
- Dの第一象限は$y=\sqrt{1-x^2}$なので以下となる。
v=4\int_{0}^{1}\int_{0}^{\sqrt{1-x^2}}\sqrt{1-x^2-y^2}dydx
この積分は普通に求まらないから数値積分してみる。
import sympy as sym
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
oo = sym.oo # 無限大
# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from scipy import integrate
print(2*np.pi/3) # 理論値
integrate.dblquad(lambda x, y: 4*np.sqrt(1-x**2-y**2), 0, 1, lambda x: 0, lambda x: np.sqrt(1-x**2))
2.0943951023931953
(2.0943951023931957, 3.5335157022586827𝑒−10)
- ここで$x=r\cosθ,y=r\sinθ$とおく。
V=\int_{0}^{2π}\int_{0}^{1}\sqrt{1−r^2}\begin{vmatrix}
\frac{∂x}{∂r} & \frac{∂x}{∂θ} \\
\frac{∂y}{∂r} & \frac{∂y}{∂θ}
\end{vmatrix} drdθ
import sympy as sym
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
oo = sym.oo # 無限大
# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from scipy import integrate
X = r * sym.cos(t)
Y = r * sym.sin(t)
Z = sym.sqrt(1-x**2-y**2).subs([(x, X), (y, Y)]).trigsimp() # 簡略化は必要(1行ずつやった方がいい)
Jacobian = sym.Matrix([[sym.diff(X, r), sym.diff(X, t)], [sym.diff(Y, r), sym.diff(Y, t)]])
sym.integrate(sym.integrate(Z * Jacobian.det().trigsimp(), (r, 0, 1)), (t, 0, 2*Pi))
\frac{2π}{3}
見方を変えればVの全領域を1で重積分しても同じ結果となる。
v=\iint_{V}dxdydz
これも$x=r\sinθ\cosφ,y=r\sinθ\sinφ,z=r\cosθ$とおく。
V=2\int_{0}^{\frac{π}{2}}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix}
\frac{∂x}{∂r} & \frac{∂x}{∂θ} & \frac{∂x}{∂φ}\\
\frac{∂y}{∂r} & \frac{∂y}{∂θ} & \frac{∂y}{∂φ}\\
\frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ}
\end{vmatrix} drdθdφ
import sympy as sym
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
oo = sym.oo # 無限大
# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from scipy import integrate
X = r * sym.sin(t) * sym.cos(u)
Y = r * sym.sin(t) * sym.sin(u)
Z = r * sym.cos(t)
Jacobian = sym.Matrix([
[sym.diff(X, r), sym.diff(X, t), sym.diff(X, u)],
[sym.diff(Y, r), sym.diff(Y, t), sym.diff(Y, u)],
[sym.diff(Z, r), sym.diff(Z, t), sym.diff(Z, u)]
])
2*sym.integrate(sym.integrate(sym.integrate(Jacobian.det().trigsimp(), (r, 0, 1)), (t, 0, Pi)), (u, 0, Pi/2))
\frac{2π}{3}
とりあえず現状では転記が精一杯。ちなみに線績分(Line Integral)・面積分(Surface Integral)・体積分(Volume Integral)を追求する過程でヤコビアン(Jacobian=ヤコビ数列)が登場する過程については以下が詳しい。
EMANの物理学>物理数学>線積分
EMANの物理学>物理数学>面積分と体積分
EMANの物理学>物理数学>ヤコビアン
\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\
=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix}
\frac{∂x}{∂r} & \frac{∂x}{∂θ} & \frac{∂x}{∂φ}\\
\frac{∂y}{∂r} & \frac{∂y}{∂θ} & \frac{∂y}{∂φ}\\
\frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ}
\end{vmatrix} drdθdφ
import sympy as sym
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
oo = sym.oo # 無限大
# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from scipy import integrate
X = r * sym.sin(t) * sym.cos(u)
Y = r * sym.sin(t) * sym.sin(u)
Z = r * sym.cos(t)
Jacobian = sym.Matrix([
[sym.diff(X, r), sym.diff(X, t), sym.diff(X, u)],
[sym.diff(Y, r), sym.diff(Y, t), sym.diff(Y, u)],
[sym.diff(Z, r), sym.diff(Z, t), sym.diff(Z, u)]
])
sym.integrate(sym.integrate(sym.integrate(Jacobian.det().trigsimp(), (r, 0, 1)), (t, 0, Pi)), (u, 0, 2*Pi))
\frac{4π}{3}
- 初等関数としての不定積分$\int e^{-x^2}dx$は存在しないが、定積分$\int_{-\infty}^{\infty} e^{-x^2}dx$は評価可能である。
- 極座標を用いてガウス積分を求めるアイデアはポアソン(1781年~1840年)まで遡る。
①平面$\mathbb {R}^2$上の函数$e^{−(x2+y2)} = e^{−r^2}$を考え、これを2通りの方法で計算する。
- 直交座標系に関する二重積分として計算し、その値は求める値の平方になることを確かめる。
- 極座標系に関する二重積分(いわゆるバウムクーヘン積分)として計算し、その値が π となることを確かめる。
②広義積分が現れることに注意して、これら2つの計算を比較して積分の値が求まる。即ち、面積要素$dA$が xy-直交座標系では$dA=dxdy$, rθ-極座標系では$dA=rdrdθ$で与えられることに注意すれば、前者と後者はそれぞれ以下の様に計算される。
\int _{\mathbb {R}^2}e^{-(x^2+y^2)}dA=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-(x^2+y^2)}dxdy=(\int_{-\infty }^{\infty }e^{-t^2}dt)^2
および
\int _{\mathbb {R}^2}e^{-(x^2+y^2)}dA=\int_{0}^{2π}\int_{0}^{π}e^{-r^2}rdrdθ\\
=2π\int_{0}^{\infty }r e^{-r^2}dr=π\int_{-\infty }^{0}e^sds=π
③後者では$s=−r^2$なる置換を行って、$ds=−2rdr$となることを用いた。これらの結果から以下となる。
(\int_{-\infty }^{\infty }e^{-x^2}dx)^2=π
④符号を考慮して以下となる。
\int_{-\infty }^{\infty }e^{-x^2}dx=\sqrt{π}
- 直交座標を用いてガウス積分を求めるアイディアはラプラス(1812年)にまで遡れる。
①$y=xs,dy=xds$と置くと、yを±∞へ近づけるときsの極限はxの符号で決まる。そして$e^{-x^2}$は偶函数なので実数全体にわたる積分が正の実数全体にわたる積分の2倍になる事から以下の様な形で計算を簡単にする事が出来る。
\int_{-\infty}^{\infty}e^{-x^2}dx=2\int_{0}^{\infty }e^{-x^2}dx
②すなわち積分範囲を x ≥ 0 に限れば、変数 y と s とは同じ極限を持ち以下が成立する。
I^2=4\int_{0}^{\infty}\int_{0}^{\infty }e^{-(x^{2}+y^{2})}dydx
③そこから以下の展開で所期の$I=\sqrt{π}$を得る。
\frac{I^2}{4}=\int _{0}^{\infty}(\int_{0}^{\infty}e^{-(x^2+y^2)}dy)dx=\int_{0}^{\infty}(\int_{0}^{\infty}e^{-x^2}(1+s^{2})xds)dx\\
=\int_{0}^{\infty}(\int_{0}^{\infty}e^{-x^2}(1+s^{2})xdx)ds=\frac{1}{2}\int_{0}^{\infty}{\frac{ds}{1+s^2}}\\
={\frac{1}{2}}\arctan s|_{0}^{\infty }={\frac {\pi }{4}}
ところで、ガウス関数の正体は「対数尺に放り込む事によって発散の方向をX軸に歪めた放物線」に他なりません。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。

この何処に円要素が? 実は正規分布(Normal Distribution)として知られるベルカーブ$y=e^{-(x^2+y^2)}$は、3次元的には以下の様に同心円的堆積を構成するのです。
【初心者向け】正規分布(Normal Distribution)とは何か?
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib.animation as animation
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x = y = np.arange(-15, 15, 0.5)
X, Y = np.meshgrid(x, y)
def dg(n):
plt.cla()
sigma = 4
Z = np.exp(-(X**2 + Y**2)/(2*sigma**2)) / (2*np.pi*sigma**2)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,cmap="summer")
# グラフを回転
ax.view_init(elev=45, azim=Time_code[n])
Time_code=num.arange(0,360,6)
ani = animation.FuncAnimation(fig, dg, interval=50,frames=len(Time_code))
ani.save("output400.gif", writer="pillow")
という事はつまり…そんな感じで以下続報。

