微分積分学
数の扱い方
数式と関数
グラフを描く (本文中のplot関数はここで作ってます)
と進めてきてようやく数学的らしいことを議論できる土台が整ったので微積をやってみる。
import
import sympy as sym
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
oo = sym.oo # 無限大
# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
極限
sympyでは無限大としてoo = sym.ooが使われる。
右側極限
$$\lim_{n\to +0}\frac{1}{n} = \infty$$
sym.limit(1/x, x, 0)
左側極限
$$\lim_{n\to -0}\frac{1}{n} = -\infty$$
sym.limit(1/x, x, 0, dir='-')
2変数関数
sym.limit((x**3+y**3)/(x-y), x, y)
$\infty$sign$(y^3)$
これはおそらく$x\to y+0$を計算している。
問
次の極限を計算せよ。
$$\lim_{x\to \infty}\frac{2^{(3x-1)}}{(x^4e^{x})^2}$$
Y = x**4 * E**x
sym.limit(2**(3*x-1)/(Y**2), x, oo)
$$\infty$$
plot(2**(3*x-1)/(Y**2), (650, 730, 1), (0, 100), close=True)
テイラー展開
関数$f(x)$の$x=a$でのテイラー展開は
$$\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$$
$f(x)=\frac{\sin(x)}{x}$をテイラー展開してみる。
sym.series(sym.sin(x)/x, x, x0=0, n=15)
$$1 - \frac{x^{2}}{6} + \frac{x^{4}}{120} - \frac{x^{6}}{5040} + \frac{x^{8}}{362880} - \frac{x^{10}}{39916800} + \frac{x^{12}}{6227020800} - \frac{x^{14}}{1307674368000} + \mathcal{O}\left(x^{15}\right)$$
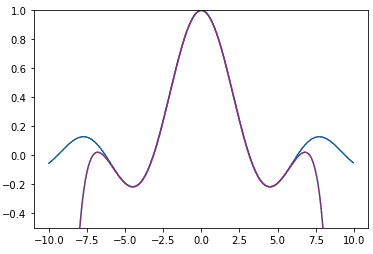
plot(sym.sin(x)/x, (-10, 10, 0.05), (-0.5, 1), cn=10)
plot(1 - x**2/6 + x**4/120 - x**6/5040 + x**8/362880
- x**10/39916800 + x**12/6227020800 - x**14/1307674368000, (-10, 10, 0.05), (-0.5, 1), close=True)
微分
微分とは微小な変分を調べるもので接戦の傾きなど関数の計量に役立つ。
sym.diff(関数, 微分するシンボル(いくつでも))で求められる。
sym.diff((sym.tan(x)*x)/(x+sym.log(x)), x)
$$\frac{x \left(-1 - \frac{1}{x}\right) \tan{\left (x \right )}}{\left(x + \log{\left (x \right )}\right)^{2}} + \frac{x \left(\tan^{2}{\left (x \right )} + 1\right)}{x + \log{\left (x \right )}} + \frac{\tan{\left (x \right )}}{x + \log{\left (x \right )}}$$
微分は積、分数、合成関数の微分なども公式で計算できるので、
微分できる関数の組み合わせだと微分可能だと思っていい。
sym.diff(x**4+sym.exp(2*x), x, 4) # 4階微分
$$8(2e^{2x}+3)$$
sym.diff(x**3 * y**5 * z, x, y, 2, z) # xで微分→yで2階微分→zで微分
$$60x^2y^3$$
偏微分の記号のまま残す
XX = sym.Derivative((x**5 * y**2 * z**4), x, y, z)
XX
$$\frac{\partial^{3}}{\partial x\partial y\partial z} \left(x^{5} y^{2} z^{4}\right)$$
sympyでは大文字の関数は遅延評価用。(数式表示用)
遅延評価
XX.doit()
$$40x^4yz^3$$
積分
積分とは面積や体積を計量するもの。
不定積分
sym.integrate(y/x, x)
$$y\log(x)$$
定積分
$$\int_1^{\infty}\frac{1}{x^2}dx$$
sym.integrate(1/x**2, (x, 1, oo))
1
積分は微分と違って求まるとは限らない。
sym.integrate(sym.sin(x)/(1+sym.exp(x)), (x, 0, Pi))
$$\int_{0}^{\pi} \frac{\sin{\left (x \right )}}{e^{x} + 1}\, dx$$
そこで数値積分する。
X = lambda x: np.sin(x)/(1+np.exp(x))
from scipy import integrate
print(integrate.quad(X, 0, np.pi))
(0.38522681353410615, 1.0755139989210769e-14) # 2つ目は推定誤差
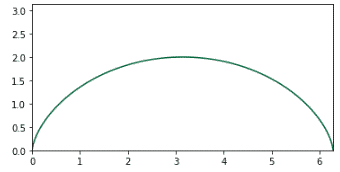
サイクロイドの面積
X = (t-sym.sin(t))
Y = (1-sym.cos(t))
plotp([X, Y], (0, 2* np.pi, 400), [0, 2 * np.pi, 0, np.pi], figs=(6, 3), close=True)
sym.integrate(Y * sym.diff(X, t), (t, 0, 2*Pi))
$3\pi$
特殊関数
ディラックのデルタ関数
D = sym.DiracDelta(x)
D
$$\delta(x)$$
sym.integrate(D, (x, -1, 1))
$1$
$x=0$以外では0だが0を含む区間で積分すると1になる。
$x=0$の1点に面積1が集中しているイメージ。
ヘヴィサイドのステップ関数
H = sym.Heaviside(x)
plot(H,(-1, 1, 0.01), (-0.5, 1.5), close=True)
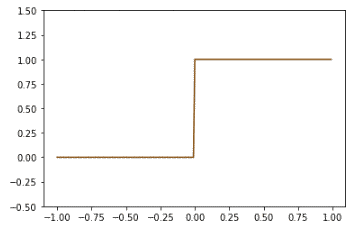
デルタの積分がステップ、ステップの微分がデルタである。
$x<0$を考えたくないからステップかけるとか…。
重積分
$z=\sqrt{1-x^2-y^2}$と$z=0$で囲まれる部分の体積を求めてみよう。
言わずと知れた半球である。
V=\int\!\!\!\int_D \!\sqrt{1-x^2-y^2} dxdy
$D$の第一象限は$y=\sqrt{1-x^2}$だから、
V=4\int_0^1\!\!\!\int_0^{\sqrt{1-x^2}} \!\!\!\sqrt{1-x^2-y^2} dydx
この積分は普通に求まらないから数値積分してみる。
print(2*np.pi/3) # 理論値
integrate.dblquad(lambda x, y: 4*np.sqrt(1-x**2-y**2), 0, 1, lambda x: 0, lambda x: np.sqrt(1-x**2))
2.0943951023931953
(2.0943951023931957,3.5335157022586827e−10)
さて$x=r\cos{\theta}, y=r\sin{\theta}$とおくと、
V=\int_0^{2\pi} \!\!\! \int_0^1 \!\!\sqrt{1-r^2}\ \begin{vmatrix}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \\
\end{vmatrix} drd\theta
X = r * sym.cos(t)
Y = r * sym.sin(t)
Z = sym.sqrt(1-x**2-y**2).subs([(x, X), (y, Y)]).trigsimp() # 簡略化は必要(1行ずつやった方がいい)
Jacobian = sym.Matrix([[sym.diff(X, r), sym.diff(X, t)], [sym.diff(Y, r), sym.diff(Y, t)]])
sym.integrate(sym.integrate(Z * Jacobian.det().trigsimp(), (r, 0, 1)), (t, 0, 2*Pi))
$$\frac{2\pi}{3}$$
見方を変えれば$V$の全領域を$1$で重積分しても同じだから
$$V=\int_V dxdydz$$
$x=r\sin{\theta}\cos{\varphi}, y=r\sin{\theta}\sin{\varphi}, z=r\cos{\theta}$とおくと、
V=2\int_0^{\!\frac{\pi}{2}}\!\!\!\int_0^{\pi}\!\!\!\int_0^1
\begin{vmatrix}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \varphi} \\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \varphi} \\
\frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \varphi} \\
\end{vmatrix}
dr d\theta d\varphi
X = r * sym.sin(t) * sym.cos(u)
Y = r * sym.sin(t) * sym.sin(u)
Z = r * sym.cos(t)
Jacobian = sym.Matrix([
[sym.diff(X, r), sym.diff(X, t), sym.diff(X, u)],
[sym.diff(Y, r), sym.diff(Y, t), sym.diff(Y, u)],
[sym.diff(Z, r), sym.diff(Z, t), sym.diff(Z, u)]
])
2*sym.integrate(sym.integrate(sym.integrate(Jacobian.det().trigsimp(), (r, 0, 1)), (t, 0, Pi)), (u, 0, Pi/2))
$$\frac{2\pi}{3}$$
線積分
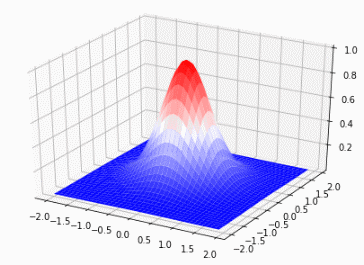
$$z=\frac{e^{-(x^2+y^2)}}{1+x^2+y^2}$$
を考える。
Z = sym.exp(-(x**2+y**2)) / (1+ x**2 + y**2)
plot3D(Z, (-2, 2, 0.1), (-2, 2, 0.1), 'surface')
X = r * sym.cos(t)
Y = r * sym.sin(t)
Z2 = Z.subs([(x, X), (y, Y)]).trigsimp()
Jacobian = sym.Matrix([[sym.diff(X, r), sym.diff(X, t)], [sym.diff(Y, r), sym.diff(Y, t)]])
result = sym.integrate(sym.integrate(Z2 * Jacobian.det().trigsimp(), (r, 0, oo)), (t, 0, 2*Pi))
sym.N(result, 30)
$1.87348049246219715751632002664$
半径1の円周上で線積分すると、
C = sym.Curve([sym.cos(t), sym.sin(t)], (t, 0, 2*Pi)) # 経路を媒介変数表示で与える
sym.line_integrate(Z, C, [x, y])
$$\frac{\pi}{e}$$
これを線積分の定義通りにやってみる。
媒介変数をそのまま代入して、
微分の自乗和の平方根を乗じて積分する。
X = sym.cos(t)
Y = sym.sin(t)
dX = sym.diff(X, t)
dY = sym.diff(Y, t)
sym.integrate(Z.subs([(x, X), (y, Y)])*sym.sqrt(dX**2 + dY**2), (t, 0, 2*Pi))
$$\frac{\pi}{e}$$