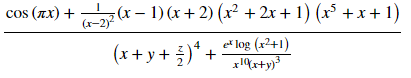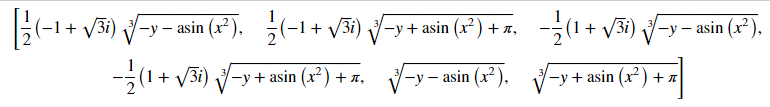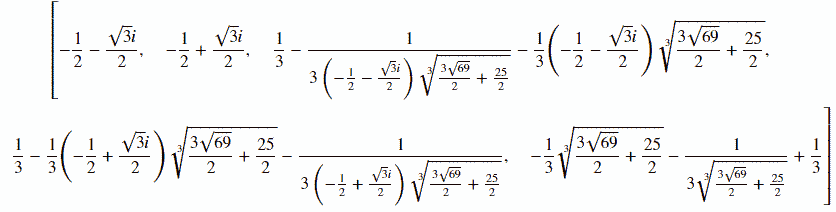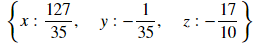数式と関数
目的など
- よくわからなかった大学の数学をPythonを使って再勉強する。(今ならMathematica並のことができるぜ)
- 数学自体が目的ではなく現実の問題を解くために数学の知識を利用したい。
- なるべく例題を入れつつ、解答は例題に特化したものではなく汎用的なものにする。
- どこがsympyの領域なのかを明確にすべくfrom sympy import *とはしない。
import sympy as sym
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')
式の定義
F1 = x * x + 2 * x + 1 # 普通にシンボルを演算するだけ
F2 = x ** 5 + x + 1 # 高次式
F3 = (x + 2) * (x - 1) / ((x - 2) * (x - 2)) # 有理関数
F4 = sym.cos(Pi * x) # 三角関数
F5 = sym.exp(x) / sym.Pow(x, 10) # 指数関数とべき乗
F6 = sym.log(x * x + 1) # 対数関数
F7 = (x + y) ** 3 # 2変数関数
F8 = (x + y + z / 2) ** 4 # 多変数関数
$x^{2} + 2 x + 1$
$x^{5} + x + 1$
$\frac{\left(x - 1\right) \left(x + 2\right)}{\left(x - 2\right)^{2}}$
$\cos{\left (\pi x \right )}$
$\frac{e^{x}}{x^{10}}$
$\log{\left (x^{2} + 1 \right )}$
$\left(x + y\right)^{3}$
$\left(x + y + \frac{z}{2}\right)^{4}$
式の展開
sym.expand(F8)
$x^{4} + 4 x^{3} y + 2 x^{3} z + 6 x^{2} y^{2} + 6 x^{2} y z + \frac{3 x^{2}}{2} z^{2} + 4 x y^{3} + 6 x y^{2} z + 3 x y z^{2} + \frac{x z^{3}}{2} + y^{4} + 2 y^{3} z + \frac{3 y^{2}}{2} z^{2} + \frac{y z^{3}}{2} + \frac{z^{4}}{16}$
因数分解
sym.factor(F1)
$(x+1)^2$
式への代入
F4.subs([(x, sym.Rational(1, 4))])
F6.subs([(x, 5)])
F8.subs([(x, 1), (y, -1), (z, 3)])
$\frac{\sqrt{2}}{2}$
$\log (26)$
$\frac{81}{16}$
式の簡略化
- powsimp (指数の簡略化),
- trigsimp (三角関数を含む式の簡略化),
- logcombine (対数関数を含む式の簡略化)
- radsimp (複素数を含む式の簡略化)
sym.radsimp((2+3*I)/(3-4*I))
$\frac{1}{25}(-6+17i)$
浮動小数への変換
print(sym.N(sym.sin(1), 30)) # 桁数を指定
print(sym.N(Pi, 50))
print(float(sym.N(Pi, 50))) # Python標準の形式に戻す
0.841470984807896506652502321630
3.1415926535897932384626433832795028841971693993751
3.141592653589793
LaTex式の出力
(F1*F2*F3+F4)/(F5*F6/F7+F8)
sym.latex((F1*F2*F3+F4)/(F5*F6/F7+F8))
\\frac{\\cos{\\left (\\pi x \\right )} + \\frac{1}{\\left(x - 2\\right)^{2}} \\left(x - 1\\right) \\left(x + 2\\right) \\left(x^{2} + 2 x + 1\\right) \\left(x^{5} + x + 1\\right)}{\\left(x + y + \\frac{z}{2}\\right)^{4} + \\frac{e^{x} \\log{\\left (x^{2} + 1 \\right )}}{x^{10} \\left(x + y\\right)^{3}}}
論文書くのに便利機能すぎる。
特定の変数について解く
F9 = x * x + sym.sin(y + z ** 3)
sym.solve(F9, z)
$F_9=0$を$z$について解いている。
まず$\sin$の逆関数で$\pm$、さらに三乗根で3倍されて計6個の解がある。
方程式を解く
sym.solve(F2, x) # F2 = x ** 5 + x + 1
解けるんかい。
解を見ると1の3乗根2つがうまく打ち消しあって
これで割れば残りは3次式というわけか。
ちなみに$x^5 + 2x + 1$だと解析的な解は求まりません。
連立方程式を解く
F10 = 2*x + 2*y + 6*z + 3
F11 = x + y - 2*z - 7
F12 = 5*x - 9*y + 2*z - 15
sym.solve([F10, F11, F12], [x, y, z])
リストを渡すだけ。簡単。
演習
-
$x=\frac{2+5i}{3-i}, y=\frac{i-2}{3i+1}$ のとき次の式の値を計算せよ。
$$\frac{1}{x^2 + 3xy - y^2}$$ -
次の式を展開せよ。
$$(a+b+c)^2-(b+c-a)^2+(c+a-b)^2-(a+b-c)^2$$ -
次の式を因数分解せよ。
$$a^2(y-b)-(a-b)xy+ab(x+y)+b^2(x-a)$$ -
次の式をPythonの通常の方法とSympyを使った方法とで比較せよ。
$$\sum_{k=0}^{10000} \sin(\frac{k}{10000})$$ -
次の方程式の解を求めよ。
$$\sin^2{x}-\cos^2{x}=0$$ -
次の連立方程式を解け。
${x^2+y^2=1},\
{y=x+\frac{1}{2}}$
X = (2+5*I)/(3-I)
Y = (I-2)/(3*I+1)
F = 1/(x*x + 3*x*y - y*y)
sym.expand(sym.radsimp(F.subs([(x, X), (y, Y)])))
$$- \frac{594}{3613} - \frac{92 i}{3613}$$
sym.expand((a+b+c)**2-(b+c-a)**2+(c+a-b)**2-(a+b-c)**2)
$$8ac$$
sym.factor(a**2 *(y-b)-(a+b)*x*y+a*b*(x+y)+b**2 *(x-a))
$$−(−a+x)(a+b)(−b+y)$$
import math
print(math.fsum([math.sin(K/10000.0) for K in range(10000)])) # Python標準
4596.556201995385
# 10秒ぐらいかかります
r = 0
for K in range(10000):
r += sym.N(sym.sin(sym.Rational(K, 10000)), 50) # なるべく内側で浮動小数にする
r
4596.5562019953847593333362996376237160871901535447
Pythonのfsumが思った以上に優秀だった。
F = (sym.sin(x) * sym.sin(x) - sym.cos(x) * sym.cos(x))
sym.solve(F, x)
$$\left [ - \frac{3 \pi}{4}, \quad - \frac{\pi}{4}, \quad \frac{\pi}{4}, \quad \frac{3 \pi}{4}\right ]$$
X = x * x + y * y - 1
Y = x - y + sym.Rational(1, 2)
sym.solve([X, Y], [x, y])
$$\left [ \left ( - \frac{1}{4} + \frac{\sqrt{7}}{4}, \quad \frac{1}{4} + \frac{\sqrt{7}}{4}\right ), \quad \left ( - \frac{\sqrt{7}}{4} - \frac{1}{4}, \quad - \frac{\sqrt{7}}{4} + \frac{1}{4}\right )\right ]$$
円と直線の交点ですね。