はじめに
Kaggleタイタニックの挑戦その2です。
今回は前処理における特徴量の作成がメインです。
備忘録の意味合いが多いのでスコアが上がる上がらないに関わらずいろんなパターンを試しています。
また、いろいろ書きすぎて記事がとても長くなっています。
・Kaggle関係の記事
Kaggleのタイタニックに挑戦してみた(その1)
Kaggleのタイタニックに挑戦してみた(その2)(ここ)
Kaggleで書いたコードの備忘録その1~データ分析で使った手法一通り~
Kaggleで書いたコードの備忘録その2~自然言語処理まとめ~
KaggleタイタニックでNameだけで予測精度80%超えた話(BERT)
コード全体
作成したコードは以下です。
前処理について
前処理は大きく欠損値の補完と特徴量の加工があります。
これらはヒューリスティックな解法がメインなようで、仮説と検証の試行錯誤になるようです。
まずは仮説を立てますが仮説は主に、
- ドメイン知識より仮説を立てる
- データを可視化し、仮説を立てる
からなり、仮説を元に特徴量を作成または加工(特徴量エンジニアリング)します。
特徴量エンジニアリングで作成した特徴量は、実際に効果があるかを検証する必要があり、この検証もヒューリスティックな部分が大きいようです。
仮説の検証は、
- 可視化により仮説を確認
- 実際に学習し評価値で確認
という感じで検証し、このサイクルを回すことでスコアを上げていきます。
参考:Kaggleにおける「特徴量エンジニアリング」の位置づけ 〜『機械学習のための特徴量エンジニアリング』に寄せて〜
import
今回使っている外部ライブラリは以下です。
# sklearn
import sklearn.model_selection
import sklearn.metrics
import sklearn.ensemble
import sklearn.preprocessing
import sklearn.ensemble
# 回帰モデル
import statsmodels.api as sm
# 数値/データ解析
import pandas as pd
import numpy as np
import scipy.stats
# ハイパーパラメータ調整
import optuna
# 表示関係
from matplotlib import pyplot as plt
import seaborn as sns
# その他
from tqdm import tqdm
学習データとテストデータの結合
特徴量の加工は学習データとテストデータ両方に実施する必要があります。
2回書くのは冗長なので最初に結合して一括で処理しちゃいます。
ただ、注意点として特徴量を分析する場合にテストデータも含めて分析されてしまうので、そこは意識して結果を見る必要があります。
# データを読み込み
df_train = pd.read_csv(os.path.join(os.path.dirname(__file__), "./titanic/train.csv"))
df_test = pd.read_csv(os.path.join(os.path.dirname(__file__), "./titanic/test.csv"))
SEED = 1234
# データを結合
df_test["Survived"] = np.nan
df = pd.concat([df_train, df_test], ignore_index=True, sort=False)
Validationの構築
特徴量を加工した後に実際に、その加工がスコアにどれだけ貢献できるかを評価する必要があります。
評価で重要な点は学習データに対するスコアではなく、汎化性能を評価することです。
学習データに対してばかりスコアをあげるといわゆる過学習と呼ばれる状態になり、テストデータのスコアが逆に下がってしまいます。
今回はValidationの手法は以下としました。
| 手法 | |
|---|---|
| (学習の種類) | (2値分類) |
| モデル | ランダムフォレスト |
| 検証手法 | K分割交差検証 |
| 評価方法 | 正解率(accuracy) |
- ランダムフォレスト
前回は複数のモデルを使っていましたが、アンサンブル学習まで手が出せなかったので今回はランダムフォレストで統一したいと思います。
- KFold(K分割交差検証)
前回でも話しましたが、学習データをk分割し k-1 個を学習、1個を検証にすることで汎化性能を評価します。(K-分割交差検証)
K分割交差検証以外にも層状K分割交差検証などいくつか種類があるようです。
- 正解率(accuracy)
そのまま正解率を使います。
ただ、2値分類の評価で意外と気づかないのが片方の正解ラベルのみを学習した場合です。
(今回ですと、全部0を正解と予測するだけで61%の正解率になる)
ですので正解率以外のバランスも見てくれるF値も確認し、閾値以下なら警告を出すようにしました。
df_train = pd.read_csv(os.path.join(os.path.dirname(__file__), "./titanic/train.csv"))
true_y = df_train["Survived"]
# 全部0の正解ラベルを作成
pred_y = [0 for _ in range(len(df_train))]
# 正解率
print(sklearn.metrics.accuracy_score(true_y, pred_y)) # 0.6161616161616161
# F値
f1 = sklearn.metrics.f1_score(true_y, pred_y)
print(f1) # 0.0
# F値が20%以下なら警告
if f1 < 0.2:
print("Warning: F1 is below the threshold.")
Validationコード
出来かぎり手軽に検証できるように関数化します。
(けどそこまでお手軽じゃないのでまだ改善の余地はありますね・・・)
def validation(
df, # 全データ(DataFrame)
select_columns, # 説明変数のリスト
target_column, # 目的変数
model_cls, # モデル
params, # モデルのパラメータ
eval_func, # 評価関数
is_pred=False, # 予測までするか
):
# 学習用データを作成
# target_columnがnullじゃないデータ(学習データ)が対象
df_train = df[df[target_column].notnull()].copy()
# 交差検証
metrics = []
kf = sklearn.model_selection.KFold(n_splits=3, shuffle=True, random_state=SEED)
#kf = sklearn.model_selection.StratifiedKFold(n_splits=3, shuffle=True, random_state=SEED)
for train_idx, true_idx in kf.split(df_train):
df_train_sub = df_train.iloc[train_idx]
df_true_sub = df_train.iloc[true_idx]
train_x = df_train_sub[select_columns]
train_y = df_train_sub[target_column]
true_x = df_true_sub[select_columns]
true_y = df_true_sub[target_column]
# 学習
model = model_cls(**params)
model.fit(train_x, train_y)
pred_y = model.predict(true_x)
# 評価結果を保存
metrics.append(eval_func(true_y, pred_y))
# 交差検証の結果は平均を採用する
metrics_mean = np.mean(metrics, axis=0)
# 評価結果を返す
if is_pred:
train_x = df_train[select_columns]
train_y = df_train[target_column]
test_x = df[df[target_column].isnull()][select_columns]
model = model_cls(**params)
model.fit(train_x, train_y)
pred_y = model.predict(test_x)
return metrics_mean, pred_y
return metrics_mean
検証および追加で実際に予測した結果も返せるようにしています。
(ほぼ同じ処理ですからね)
実際に使う例は以下です。
df = 学習データとテストデータが入ったDataFranm
select_columns = 説明変数のカラム名のリスト
target_column = 目的変数のカラム名("Survived")
# モデル
model_cls = sklearn.ensemble.RandomForestClassifier
model_params = {"random_state": SEED}
# 評価方法(accuracyの場合)
def eval_func(true_y, pred_y):
return sklearn.metrics.accuracy_score(true_y, pred_y)
# 評価
metric = validation(df, select_columns, target_column, model_cls, model_params, eval_func)
ベースラインモデルの構築
評価方法が決まったので次は基準となるモデルを作成します。
ベースラインモデルは新しい特徴量を作成した場合にそれが良いのか悪いのかを比較する基準となるモデルです。
基準として性別のみで予測しているモデルを基準にしました。
# ダミー変数名を取得用
def generate_to_dummy_name(df, columns, dummy_columns):
names = []
for c in columns:
if c in dummy_columns:
for uniq in df[c].unique():
names.append("{}_{}".format(c, uniq))
else:
names.append(c)
return names
# ベースラインをもとに検証する
def valid_baseline_diff(
df, # 全データ(DataFrame)
remove_columns, # 削除する説明変数
add_colums, # 追加する説明変数
dummy_columns # ダミー化する変数
):
df = df.copy()
# 欠損値がある場合はなくす
df["Age"].fillna(df["Age"].median(), inplace=True)
df["Embarked"].fillna("S", inplace=True)
df["Cabin"].fillna('Unknown', inplace=True)
df["Fare"].fillna(df["Fare"].median(), inplace=True)
# 基本となる説明変数
select_columns = [
#"Age",
#"SibSp",
#"Parch",
#"Fare",
#"Pclass",
"Sex",
#"Embarked",
]
# 説明変数を除外
for c in remove_columns:
select_columns.remove(c)
# 説明変数を追加
select_columns.extend(add_colums)
select_columns = list(set(select_columns)) # 念のためuniq
# あるカラムのみ
dummy_columns = list(set(dummy_columns) & set(select_columns))
# カラム名をダミー名に
select_columns = generate_to_dummy_name(df, select_columns, dummy_columns)
# ダミー化
df = pd.get_dummies(df, columns=dummy_columns)
# モデル
model_cls = sklearn.ensemble.RandomForestClassifier
model_params = {"random_state": SEED}
# 評価
def eval_func(true_y, pred_y):
f1_threshold = 0.2 # f1閾値
# F1値の警告
f1 = sklearn.metrics.f1_score(true_y, pred_y)
if f1 < f1_threshold:
print("Warning: F1 is below the threshold.({} < {})".format(f1, f1_threshold))
return sklearn.metrics.accuracy_score(true_y, pred_y)
metric = validation(df, select_columns, "Survived", model_cls, model_params, eval_func)
s = "metric: {} ({}):{} ".format(metric, len(select_columns), sorted(select_columns))
print(s)
return s
# 実行
baseline_str = valid_baseline_diff(df, [], [], ["Sex"])
# metric: 0.78675645342312 (13):['Sex_female', 'Sex_male']
1.特徴量エンジニアリング
特徴量を加工していきます。
基本方針としては元データを保持したまま、新しい特徴量を追加していく形で実装しています。
分析に使う手法の関数化
いくつか関数化しておきます。
あるカラムと他のカラムの関係
あるカラムに対して他のカラムがどの程度影響しているかを見る関数を作成しておきます。
相関係数とランダムフォレストの重要度と重回帰分析の結果を見る関数です。
def compute_correlation_relationship(
df,
select_columns,
target_column,
pred_type,
):
df = df[df[target_column].notnull()].copy()
select_columns = list(select_columns)
if target_column in select_columns:
select_columns.remove(target_column)
# 教師データを作成
x = df[select_columns]
y = df[target_column]
df_result = pd.DataFrame(select_columns)
df_result.columns = ["name"]
df_result = df_result.set_index("name")
# 相関係数
corr = df.corr()[target_column]
df_result["corr"] = corr.drop([target_column], axis=0)
# ランダムフォレスト
if pred_type == "Classifier":
model = sklearn.ensemble.RandomForestClassifier(random_state=SEED)
elif pred_type == "Regressor":
model = sklearn.ensemble.RandomForestRegressor(random_state=SEED)
else:
raise ValueError()
model.fit(x, y)
df_result["RandomForest"] = model.feature_importances_
# 重回帰分析
model = sm.OLS(y, sm.add_constant(x))
fitted = model.fit()
if len(fitted.params) == len(select_columns):
df_result["OLS_val"] = list(fitted.params)
df_result["OLS_p"] = list(fitted.pvalues)
elif len(fitted.params) == len(select_columns)+1:
df_result["OLS_val"] = list(fitted.params)[1:]
df_result["OLS_p"] = list(fitted.pvalues)[1:]
return df_result
sns.countplotの拡張
あるカラムに関して目的変数との関係を集計して表示したい場合があります。
その時によく使われるのが sns.countplot ですが、hue で分割したカラムに対して元の割合だとどうだったかを比較したい場合がよくありました。
それっぽいのがなかったので作成してみました。
def plot_count_category(df, column, hue_column):
# 欠損値が入っているデータは除外する
df = df.dropna(subset=[column, hue_column]).copy()
# 型を変換
df[column] = df[column].astype(str)
df[hue_column] = df[hue_column].astype(str)
# マージンを設定
margin = 0.2
totoal_width = 1 - margin
# hue_data
hue_counts = df[hue_column].value_counts()
hue_keys = hue_counts.keys()
# clumn_data
column_keys = df[column].value_counts().keys()
hue_column_counts = {}
for k2 in hue_keys:
hue_column_counts[k2] = []
for k in column_keys:
c = df[df[column]==k][hue_column].value_counts()
# hue key毎に分けておく
for k2 in hue_keys:
if k2 in c:
hue_column_counts[k2].append(c[k2])
else:
hue_column_counts[k2].append(0)
column_counts = []
for k in column_keys:
c = len(df[df[column]==k])
column_counts.append(c)
# barの座標を計算
bar_count = len(hue_keys)
bar_width = totoal_width/bar_count
x_bar_pos = np.asarray(range(bar_count)) * bar_width
for i, k in enumerate(hue_keys):
counts = hue_column_counts[k]
# barを表示
x_pos = np.asarray(range(len(counts)))
x_pos = x_pos + x_bar_pos[i] - (bar_count * bar_width) / 2 + bar_width / 2
plt.bar(x_pos, counts, width=bar_width, label=hue_keys[i])
# 線を表示
p_all = (hue_counts[k] / hue_counts.sum())
c = np.asarray(column_counts) * p_all
plt.hlines(c, xmin=x_pos - bar_width/2, xmax=x_pos + bar_width/2, colors='r', linestyles='dashed')
plt.xticks(range(len(column_keys)), column_keys)
plt.xlabel(column)
plt.legend(title=hue_column)
plt.show()
# 性別と生存率の例
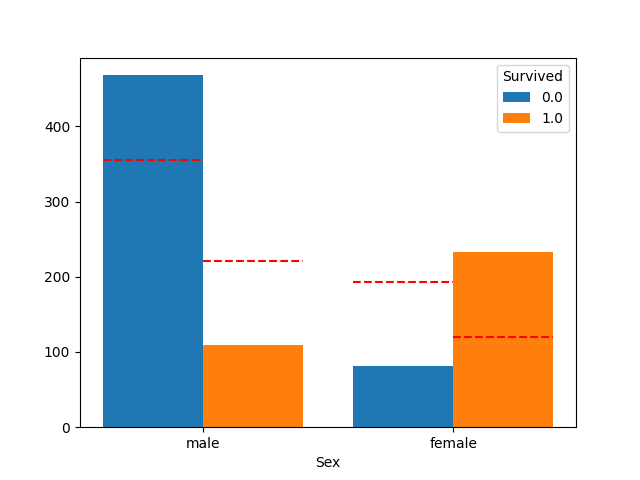
plot_count_category(df, "Sex", "Survived")
思ったより作成が大変でした…。
棒の部分は sns.countplot の結果と変わりません。
赤線の部分が追加箇所で、全体の生存率の比率のまま分割した場合の線となります。
その他plot関係
目的別に使うものは関数にしています。(逆引き的な)
# カテゴリ別に結果を表示したい場合
def plot_category_bar(df, column):
df[column].plot.barh()
plt.title(column)
plt.tight_layout()
plt.show()
# 小数データをヒストグラムで表示
def plot_float(df, column, bins=10):
sns.distplot(df[column], kde=True, rug=False, bins=bins)
plt.title(column)
plt.tight_layout()
plt.show()
# カテゴリデータに対する小数データを見たいとき
def plot_category_float(
df,
column1,
column2,
bins=10,
is_overlap=True,
write_line=None
):
for uniq in df[column1].unique():
if uniq is np.nan:
continue
sns.distplot(df[df[column1]==uniq][column2], kde=True, rug=False, bins=bins, label=uniq)
if write_line is not None:
plt.axvline(x=write_line, color="red")
if not is_overlap:
plt.legend()
plt.show()
if is_overlap:
plt.legend()
plt.show()
# 小数データに対するカテゴリを見たいとき
def plot_float_category(
df,
column1,
column2,
bins=10,
is_overlap=True,
write_line=None
):
plot_category_float(
df,
column2,
column1,
bins=10,
is_overlap=True,
write_line=None
)
候補変数とdummy変数の管理
ダミー化の工程がちょっと厄介でした。
管理しやすいようにダミー化する変数は別途保存しておきます。
# 特徴量を作成したら都度追加していく
dummy_columns = ["Pclass", "Sex", "Embarked"]
kouho_columns = ["Pclass", "Sex", "Embarked"]
1-1.Embarked 乗船港 (欠損値)
乗船港の欠損値を埋めます。
データは2件だけですので実際に見てみます。
print(df['Embarked'].unique())
# 見ずらくなるのでNameは除外
print(df[df["Embarked"].isnull()].drop(["Name"], axis=1).T)
['S' 'C' 'Q' nan]
61 829
PassengerId 62 830
Survived 1.0 1.0
Pclass 1 1
Sex female female
Age 38.0 62.0
SibSp 0 0
Parch 0 0
Ticket 113572 113572
Fare 80.0 80.0
Cabin B28 B28
Embarked NaN NaN
いくつか仮説を立ててみます。
- Ticketが同じなので、他に同じチケットがあれば同じ乗船港では?
- Pclass(チケットクラス)とFare(チケットの値段)が関係ありそう
まずはTicketから見ていきます。
print(len(df[df["Ticket"]=="113572"])) # 2
残念ながら同じチケットはこの2人しかいませんでした。
次に少し丁寧ですが、まずは Embarked と他のカラムとの相関関係を見てみます。
(Embarkedが[Pclass, Fare]と相関があるかを確認します)
# 比較に使うカラムを選択
df2 = df[[
#"PassengerId", # ユニークIDなので除外
#"Survived", # 目的変数なので除外
"Pclass",
"Sex",
"Age",
"SibSp",
"Parch",
#"Ticket", # よくわからない要素なので除外
"Fare",
#"Catbin", # 欠損値が多いので除外
"Embarked",
]].copy()
# 欠損値を仮保管
df2["Age"].fillna(df2["Age"].median(), inplace=True)
df2["Embarked"].fillna("S", inplace=True)
df2["Fare"].fillna(df2['Fare'].median(), inplace=True)
# 正規化(重回帰分析用)
df2["Age"] = sklearn.preprocessing.StandardScaler().fit_transform(df2["Age"].to_numpy().reshape((-1, 1)))
df2["Fare"] = sklearn.preprocessing.StandardScaler().fit_transform(df2["Fare"].to_numpy().reshape((-1, 1)))
# ダミー化
df2 = pd.get_dummies(df2, columns=["Pclass", "Sex"])
# ラベル化(対象をダミー化すると3パターン比較しないといけないので)
df2["Embarked"] = sklearn.preprocessing.LabelEncoder().fit_transform(df2["Embarked"])
# 相関結果を表示
cr = compute_correlation_relationship(df2, df2.columns, "Embarked", pred_type="Classifier")
print(cr)
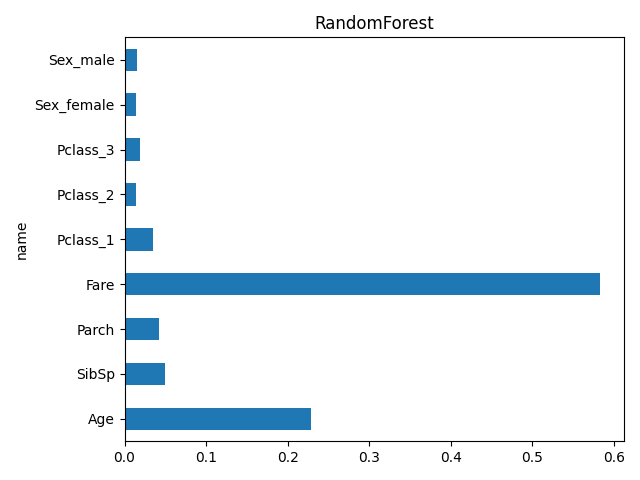
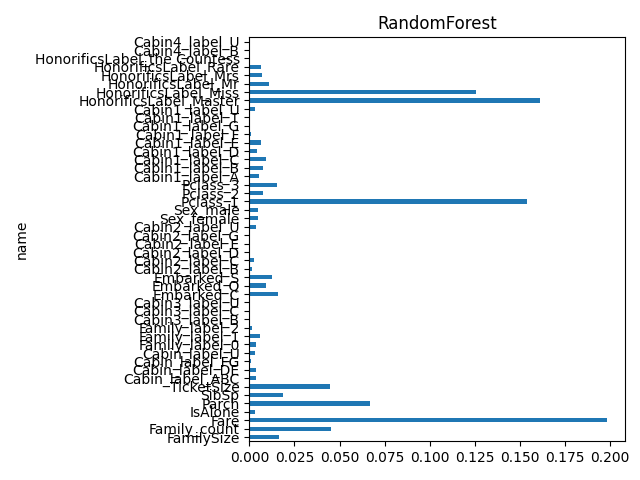
plot_category_bar(cr, "RandomForest")
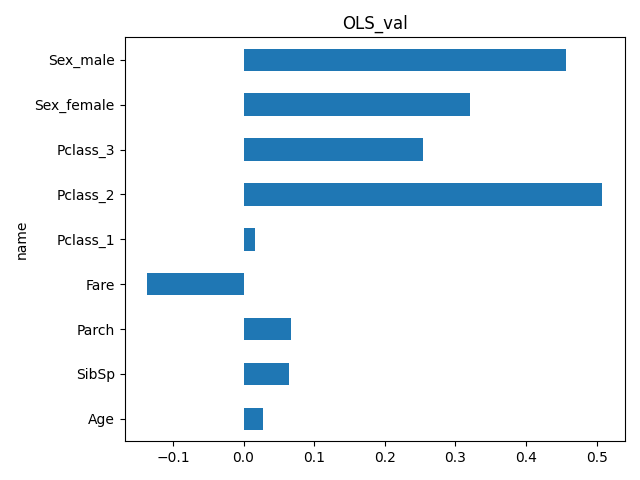
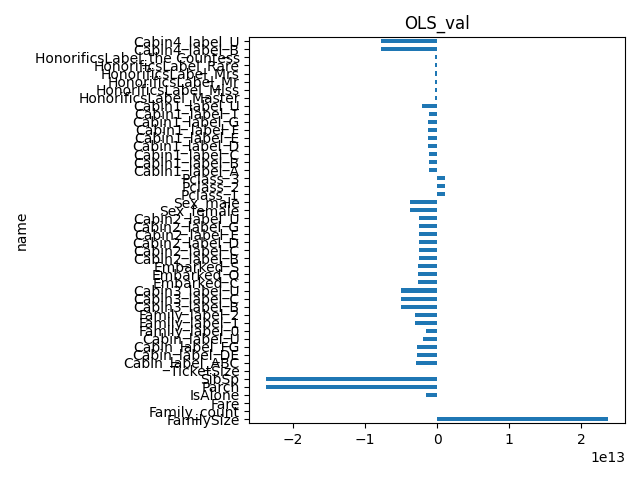
plot_category_bar(cr, "OLS_val")
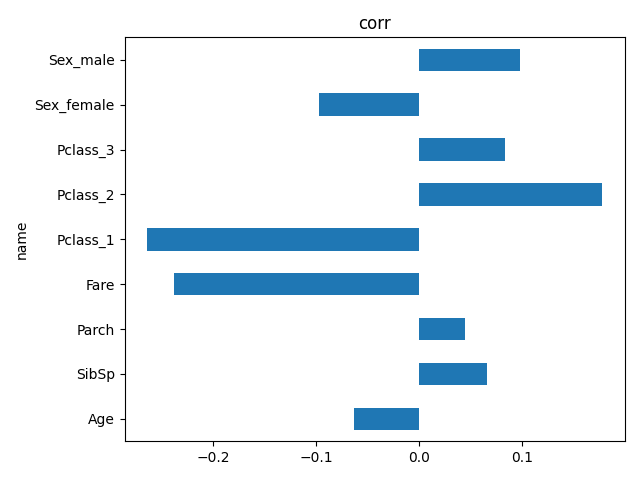
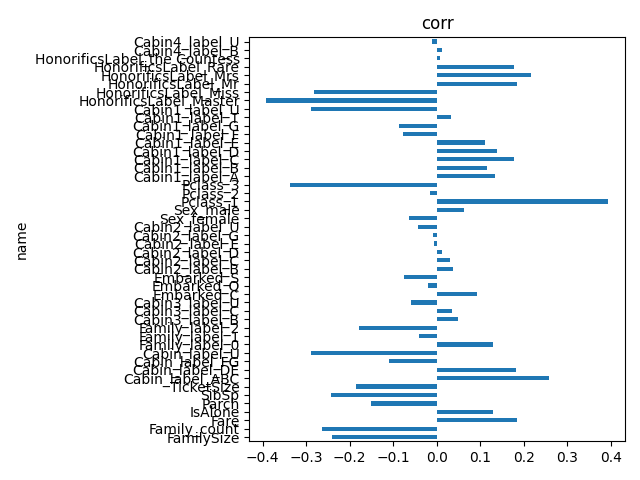
plot_category_bar(cr, "corr")
corr RandomForest OLS_val OLS_p
name
Age -0.063424 0.228185 0.027611 2.421174e-01
SibSp 0.065567 0.049574 0.065001 4.025903e-03
Parch 0.044772 0.041739 0.067426 1.479441e-02
Fare -0.238131 0.582912 -0.136273 1.582595e-06
Pclass_1 -0.264302 0.035125 0.015753 7.272290e-01
Pclass_2 0.177625 0.014007 0.507930 2.915941e-38
Pclass_3 0.083079 0.019057 0.254084 2.034077e-14
Sex_female -0.097960 0.014409 0.321258 9.255020e-33
Sex_male 0.097960 0.014993 0.456509 2.023067e-81
ランダムフォレストは Fare と Age が高め、OLS は Sex と Pclass_2 が高め、相関係数は Pclass_1 と Fare が高めですね。
Age は欠損値が多く、参考としては弱いので Fare,Pclass,Sex で Embarked を見てみます。
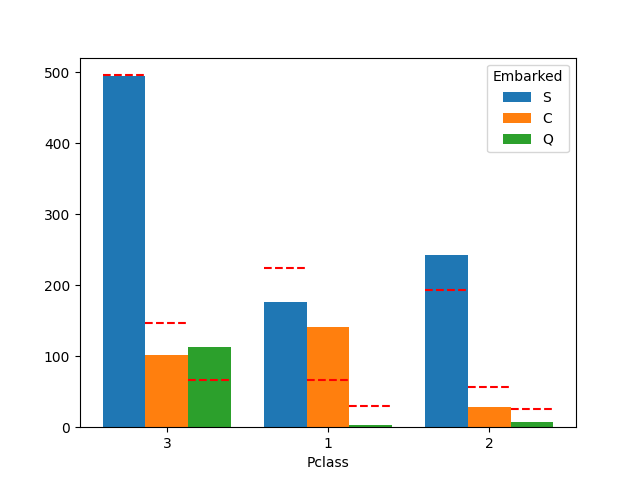
- Pclass毎のEmbarked
plot_count_category(df, "Pclass", "Embarked")
関係がありそうです。
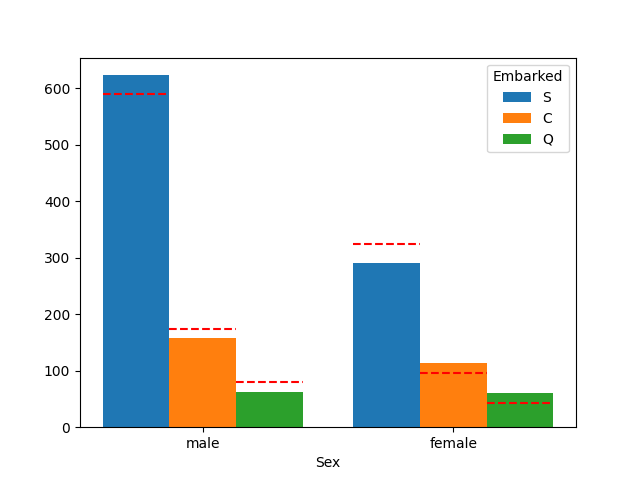
- Sex毎のEmbarked
plot_count_category(df, "Sex", "Embarked")
あまり関係なさそう?
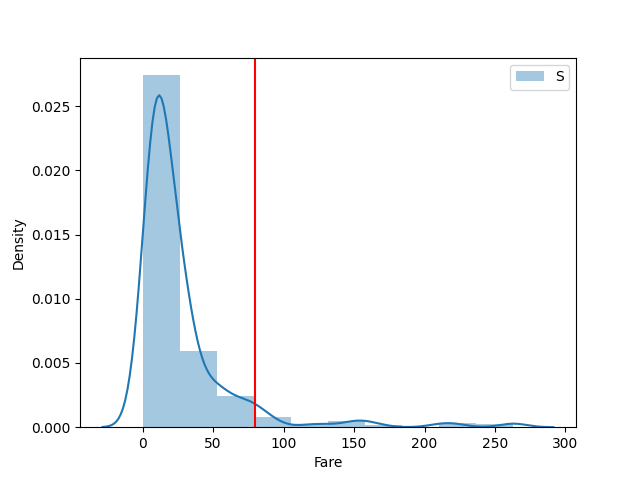
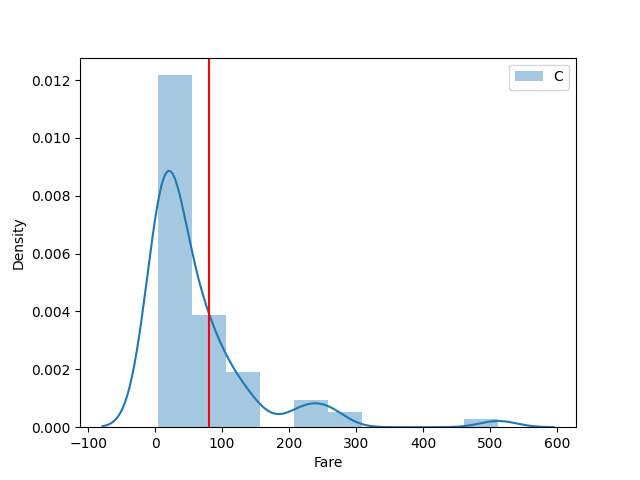
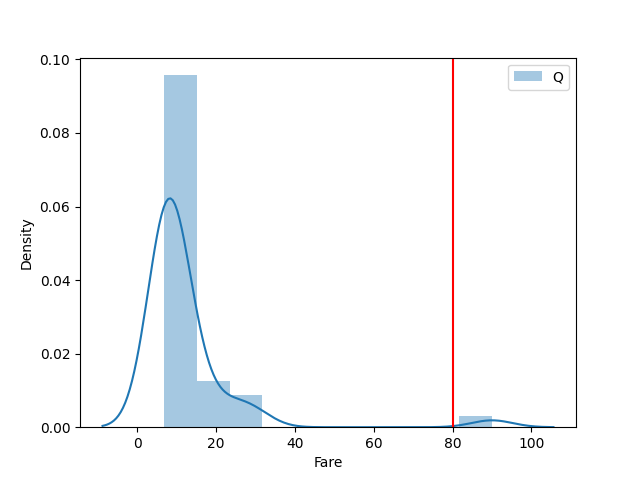
- EmbarkedとFareの関係
Fareは小数なので Embarked 毎に傾向を見てみます。
plot_category_float(df, "Embarked", "Fare", is_overlap=False, write_line=80)
Cが一番当てはまりそうですかね。
- 補完
Fareの結果よりCで補完しました。
多分使わないですが、補完フラグも追加しています。
df["Embarked_na"] = df["Embarked"].isnull().astype(np.int64)
df['Embarked'].fillna("C", inplace=True)
- おまけ
実際にこの2人の名前を検索すると情報が出てきて、Southampton(S)から乗船したようです。。。
今回はCのまま行きます。
1-2.Fare チケット料金 (欠損値)
欠損データが1件だけなので見てみます。
print(df[df["Fare"].isnull()].T)
1043
PassengerId 1044
Survived NaN
Pclass 3
Name Storey, Mr. Thomas
Sex male
Age 60.5
SibSp 0
Parch 0
Ticket 3701
Fare NaN
Cabin NaN
Embarked S
Embarked_na 0
Embarked は丁寧に見ましたが~~(疲れたので)~~1件だけですので、相関がありそうな Pclass と相関があった Embarked を元に決めます。
Pclass==3、Embarked==S のデータから中央値のデータで埋めます。
med = df[(df["Pclass"]==3) & (df["Embarked"]=="S")]['Fare'].median()
df["Fare_na"] = df["Fare"].isnull().astype(np.int64)
df["Fare"].fillna(med, inplace=True)
1-3.Fare チケット料金 (外れ値)
前回クックの距離でFareの外れ値があったので確認してみます。
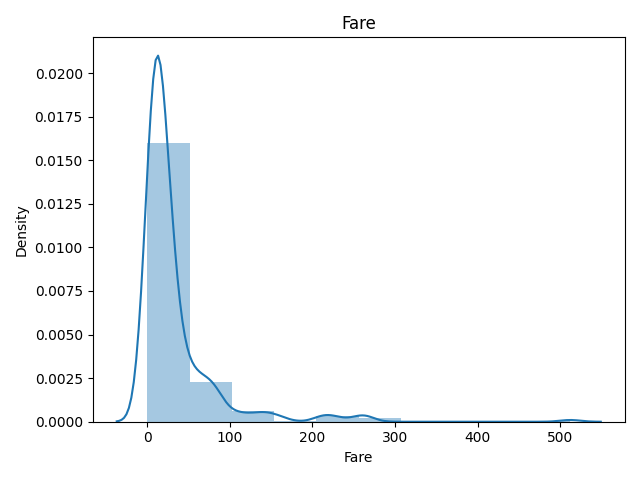
ヒストグラムは以下です。
plot_float(df, "Fare")
300や400付近はないですけど、500付近に値がありますね。
# Fareが300以上のデータ数を確認
print(len(df[df["Fare"] > 300])) # 4
データ数は4件です。
外れ値への対応は主に以下の方法があるそうです。
| 手法 | 概要 |
|---|---|
| winsorization | 下限と上限から外れる値を下限値・上限値に置き換える(1%~99%の範囲で丸めるのがいいらしい) |
| rank transformation | データに順位をつけ、順位をベースに値を置き換える方法。順位ベースなのでデータ間の間隔が等しくなる。 |
| log transformation | 対数変換 |
| square root transformation | 平方根変換 |
今回はシンプルな winsorization で外れ値に対処します。
df["Fare"] = scipy.stats.mstats.winsorize(df["Fare"], limits=[0.01, 0.01])
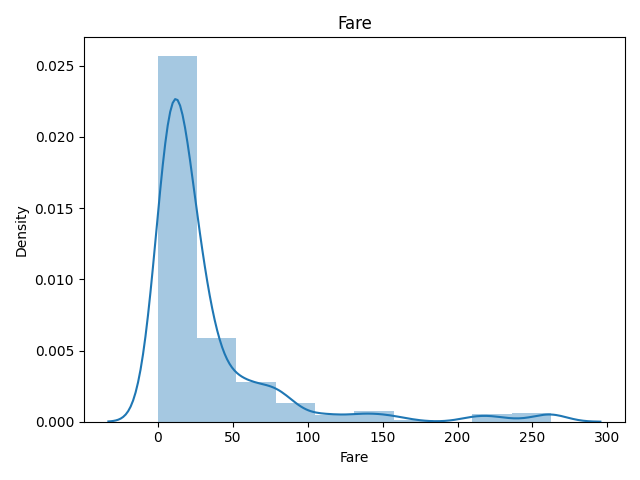
# 外れ値を除外した結果をplot
plot_float(df, "Fare")
1-4.Fareのラベル化 (新しい特徴量)
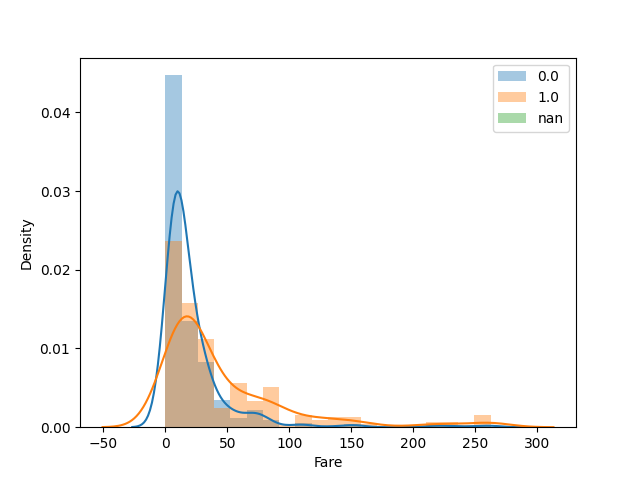
Fareについて生存率を見てみます。
plot_float_category(df, "Fare", "Survived", bins=20)
分割毎の生存率を見てみます。
print(pd.crosstab(pd.cut(df["Fare"], 20), df["Survived"], normalize='index'))
Survived 0.0 1.0
Fare
(-0.262, 13.119] 0.752336 0.247664
(13.119, 26.238] 0.577381 0.422619
(26.238, 39.356] 0.545455 0.454545
(39.356, 52.475] 0.694444 0.305556
(52.475, 65.594] 0.242424 0.757576
(65.594, 78.712] 0.516129 0.483871
(78.712, 91.831] 0.233333 0.766667
(91.831, 104.95] 0.000000 1.000000
(104.95, 118.069] 0.363636 0.636364
(118.069, 131.188] 0.000000 1.000000
(131.188, 144.306] 0.142857 0.857143
(144.306, 157.425] 0.333333 0.666667
(157.425, 170.544] 0.000000 1.000000
(209.9, 223.019] 0.400000 0.600000
(223.019, 236.138] 0.250000 0.750000
(236.138, 249.256] 0.500000 0.500000
(249.256, 262.375] 0.222222 0.777778
13以下、13~39、39以降で生存率に違いがありそうです。
ラベルとして特徴量を作っておきます。
def FareLabel(x):
if x < 13:
return 0
elif x < 39:
return 1
else:
return 2
df["Fare_label"] = df["Fare"].apply(FareLabel)
dummy_columns.append("Fare_label")
kouho_columns.append("Fare_label")
plotと評価してみます。
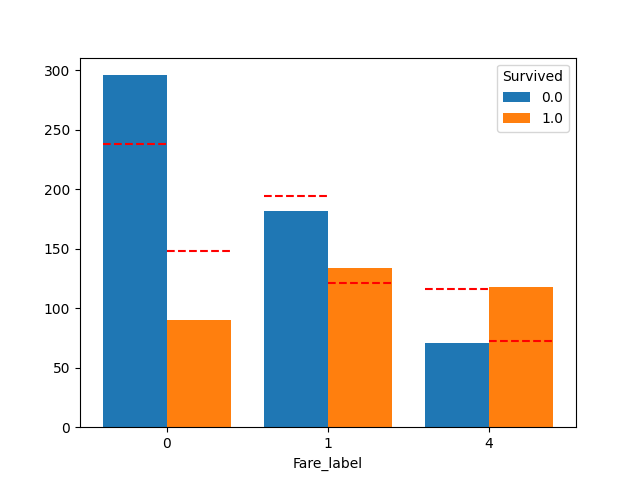
plot_count_category(df, "Fare_label", "Survived")
良い感じに分かれてそうです。
# 評価
print(baseline_str)
valid_baseline_diff(df, [], [ "Fare_label"], dummy_columns)
metric: 0.78675645342312 (2):['Sex_female', 'Sex_male']
metric: 0.78675645342312 (5):['Fare_label_0', 'Fare_label_1', 'Fare_label_2', 'Sex_female', 'Sex_male']
評価は変わりませんね…
1-5.Cabin 部屋番号 (欠損値)
Cabinのデータを見てみます。
print(df["Cabin"].isnull().sum())
print(df["Cabin"].value_counts())
1014 # 欠損データの数
C23 C25 C27 6
G6 5
B57 B59 B63 B66 5
B96 B98 4
F2 4
..
B101 1
C103 1
A21 1
D45 1
D22 1
欠損値がデータの大半を占めています。
また、データによってはスペース区切りになっていますね。
欠損値は Unknown で埋めたいと思います。
df['Cabin'] = df['Cabin'].fillna('Unknown')
1-6.Cabinの分析 (新しい特徴量)
Cabinは重要かどうかという議論があったのでリンクを張っておきます。
Is 'cabin' an important predictor?
Cabinは先頭の文字がデッキを表しているようです。
まずはスペースで分割し、その後先頭の文字を抜き出します。
df2 = df['Cabin'].str.split(" ", expand=True)
df2.columns = ["Cabin1", "Cabin2", "Cabin3", "Cabin4"]
df2 = df2.fillna('Unknown')
print(df2.head().T)
0 1 2 3 4
Cabin1 Unknown C85 Unknown C123 Unknown
Cabin2 Unknown Unknown Unknown Unknown Unknown
Cabin3 Unknown Unknown Unknown Unknown Unknown
Cabin4 Unknown Unknown Unknown Unknown Unknown
先頭の文字をラベルにしてラベル毎の生存率を見てみます。
df["Cabin1_label"] = df2['Cabin1'].str.get(0)
df["Cabin2_label"] = df2['Cabin2'].str.get(0)
df["Cabin3_label"] = df2['Cabin3'].str.get(0)
df["Cabin4_label"] = df2['Cabin4'].str.get(0)
dummy_columns.append("Cabin1_label")
dummy_columns.append("Cabin2_label")
dummy_columns.append("Cabin3_label")
dummy_columns.append("Cabin4_label")
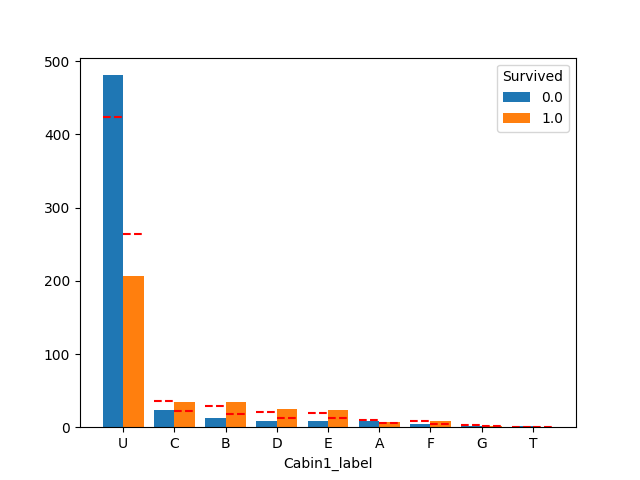
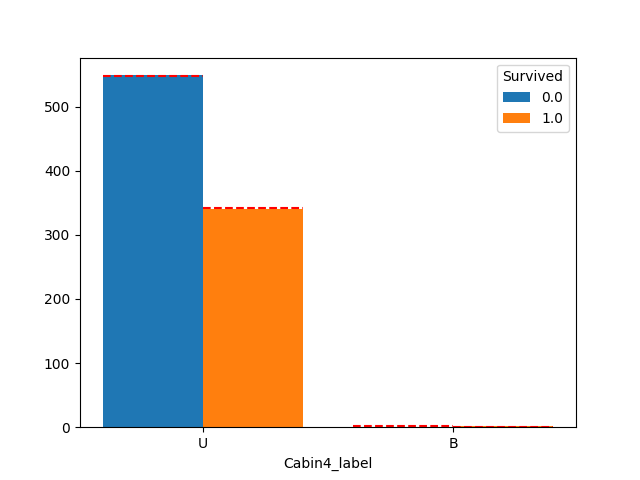
plot_count_category(df, "Cabin1_label", "Survived")
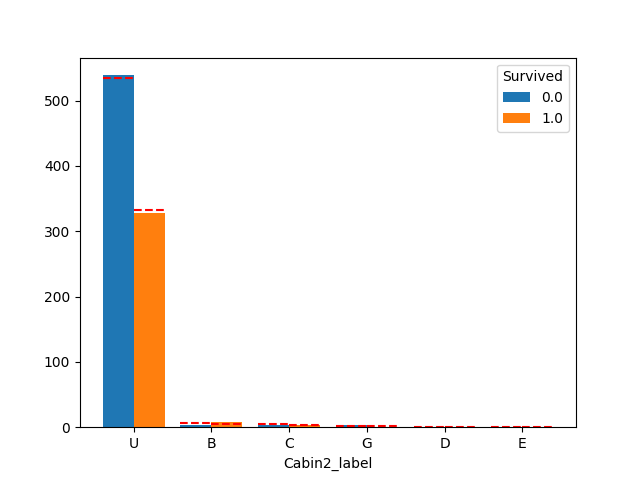
plot_count_category(df, "Cabin2_label", "Survived")
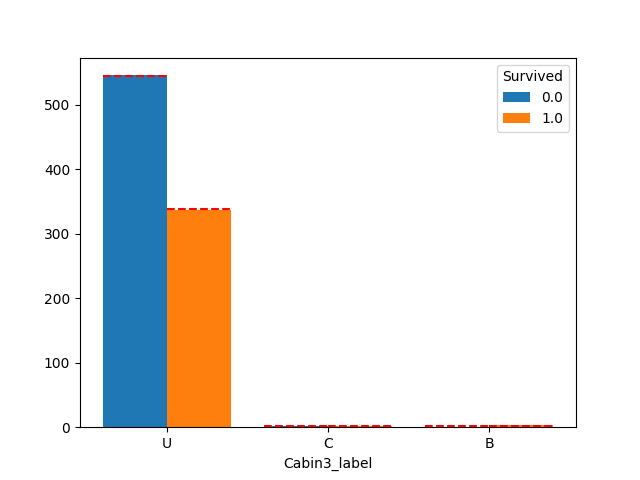
plot_count_category(df, "Cabin3_label", "Survived")
plot_count_category(df, "Cabin4_label", "Survived")
Cabin1_label は影響ありそうですが、2,3,4は生存率に影響なさそうです。
Pclassに対するCabinも見てみます。
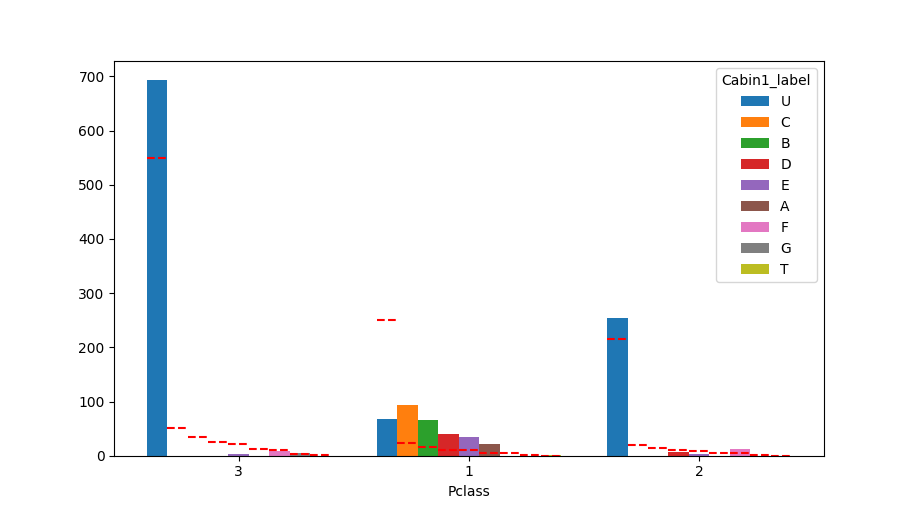
print(pd.crosstab(df["Pclass"], df["Cabin1_label"], normalize='index').T)
plot_count_category(df, "Pclass", "Cabin1_label")
Pclass 1 2 3
Cabin1_label
A 0.068111 0.000000 0.000000
B 0.201238 0.000000 0.000000
C 0.291022 0.000000 0.000000
D 0.123839 0.021661 0.000000
E 0.105263 0.014440 0.004231
F 0.000000 0.046931 0.011283
G 0.000000 0.000000 0.007052
T 0.003096 0.000000 0.000000
U 0.207430 0.916968 0.977433
ABCが1stクラスの客室だそうです。(Pclassが1しかいないですね)
DEが中流、FGが下流クラスといった感じでしょうか。
以下のようにラベリングしてみました。
def CabinLabel(x):
if x in ["A", "B", "C", "T"]:
return "ABC"
elif x in ["D", "E"]:
return "DE"
elif x in ["F", "G"]:
return "FG"
else:
return x
df['Cabin_label'] = df['Cabin1_label'].apply(CabinLabel)
dummy_columns.append("Cabin_label")
kouho_columns.append("Cabin_label")
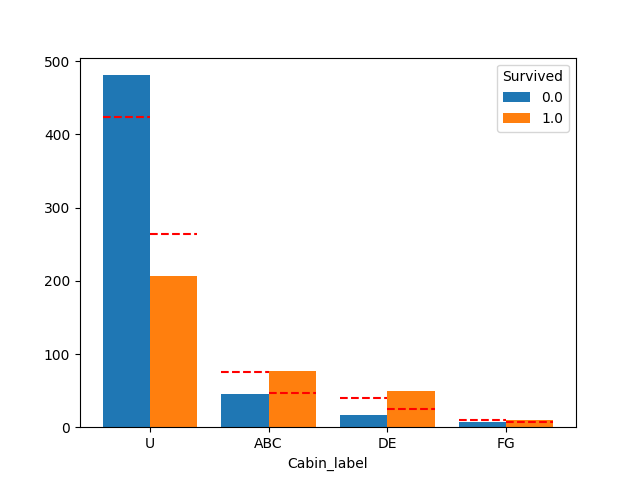
plot_count_category(df, "Cabin_label", "Survived")
良い感じに分かれてそうです。
# 評価
print(baseline_str)
valid_baseline_diff(df, [], ["Cabin1_label"], dummy_columns)
valid_baseline_diff(df, [], ["Cabin2_label"], dummy_columns)
valid_baseline_diff(df, [], ["Cabin3_label"], dummy_columns)
valid_baseline_diff(df, [], ["Cabin4_label"], dummy_columns)
valid_baseline_diff(df, [], ["Cabin_label"], dummy_columns)
etric: 0.78675645342312 (2):['Sex_female', 'Sex_male']
metric: 0.7845117845117845 (11):['Cabin1_label_A', 'Cabin1_label_B', 'Cabin1_label_C', 'Cabin1_label_D', 'Cabin1_label_E', 'Cabin1_label_F', 'Cabin1_label_G', 'Cabin1_label_T', 'Cabin1_label_U', 'Sex_female', 'Sex_male']
metric: 0.7833894500561168 (8):['Cabin2_label_B', 'Cabin2_label_C', 'Cabin2_label_D', 'Cabin2_label_E', 'Cabin2_label_G', 'Cabin2_label_U', 'Sex_female', 'Sex_male']
metric: 0.7856341189674523 (5):['Cabin3_label_B', 'Cabin3_label_C', 'Cabin3_label_U', 'Sex_female', 'Sex_male']
metric: 0.78675645342312 (4):['Cabin4_label_B', 'Cabin4_label_U', 'Sex_female', 'Sex_male']
metric: 0.7833894500561168 (6):['Cabin_label_ABC', 'Cabin_label_DE', 'Cabin_label_FG', 'Cabin_label_U', 'Sex_female', 'Sex_male']
評価があがりませんね…
1-7.家族人数 (新しい特徴量)
SibSpは同乗している兄弟/配偶者、Parchは同乗している親/子供の数を表します。
ですのでここから同乗した家族人数をだします。
また、一人とそれ以外も特徴量として出しておきます。
df["FamilySize"] = df["SibSp"] + df["Parch"] + 1
df['IsAlone'] = df["FamilySize"].apply(lambda x:x==1).astype(np.int64)
kouho_columns.append("FamilySize")
kouho_columns.append("IsAlone")
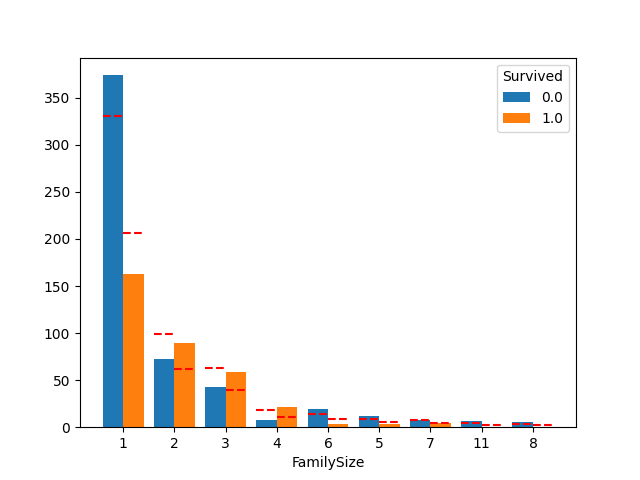
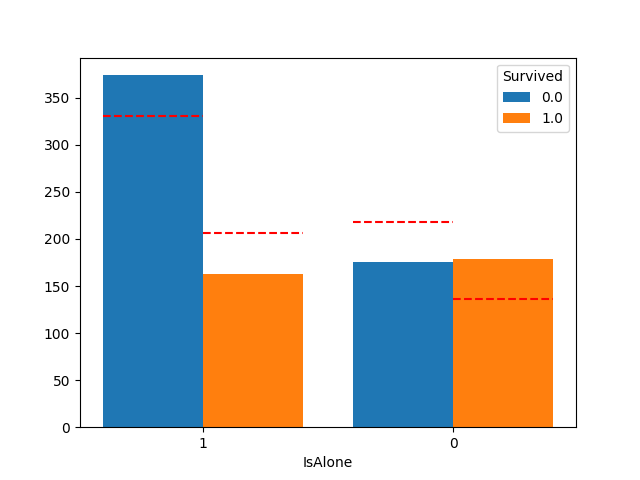
plot_count_category(df, "FamilySize", "Survived")
plot_count_category(df, "IsAlone", "Survived")
家族人数が2~4の時に生存率が逆転していますね。
これをラベルとして新しい特徴量にしておきます。
def FamilyLabel(x):
if x == 1:
return 0
elif 2 <= x and x <= 4:
return 1
else:
return 2
df["Family_label"] = df['FamilySize'].apply(FamilyLabel)
dummy_columns.append("Family_label")
kouho_columns.append("Family_label")
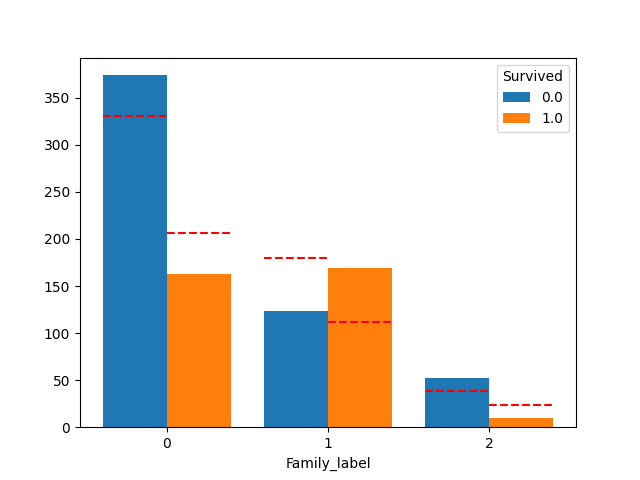
plot_count_category(df, "Family_label", "Survived")
print(baseline_str)
valid_baseline_diff(df, [], [ "FamilySize"], dummy_columns)
valid_baseline_diff(df, [], [ "IsAlone"], dummy_columns)
valid_baseline_diff(df, [], [ "Family_label"], dummy_columns)
metric: 0.78675645342312 (2):['Sex_female', 'Sex_male']
metric: 0.7957351290684623 (3):['FamilySize', 'Sex_female', 'Sex_male']
metric: 0.78675645342312 (3):['IsAlone', 'Sex_female', 'Sex_male']
metric: 0.8035914702581369 (5):['Family_label_0', 'Family_label_1', 'Family_label_2', 'Sex_female', 'Sex_male']
Family_labelでやっと評価が上がりましたね。
1-8.Nameの分析 敬称 (新しい特徴量)
名前は"苗字,敬称,名"という形で構成されているようです。
print(df["Name"].head())
0 Braund, Mr. Owen Harris
1 Cumings, Mrs. John Bradley (Florence Briggs Th...
2 Heikkinen, Miss. Laina
3 Futrelle, Mrs. Jacques Heath (Lily May Peel)
4 Allen, Mr. William Henry
Name: Name, dtype: object
まずは敬称を抜き出してみます。
df["Honorifics"] = df['Name'].apply(lambda x: x.split(",")[1].split(".")[0].strip())
print(pd.crosstab(df['Honorifics'], df['Survived'].isnull()))
Survived False True
Honorifics
Capt 1 0
Col 2 2
Don 1 0
Dona 0 1
Dr 7 1
Jonkheer 1 0
Lady 1 0
Major 2 0
Master 40 21
Miss 182 78
Mlle 2 0
Mme 1 0
Mr 517 240
Mrs 125 72
Ms 1 1
Rev 6 2
Sir 1 0
the Countess 1 0
左が学習データのみにある敬称の数、右がテストデータのみにある敬称の数です。
学習データのみにある敬称はテストデータの邪魔になるので学習データから除外するという方法を行っている人もいました。
少ないデータもあるので敬称の意味である程度まとめます。
"""敬称一覧
Mr:男 ,
Master:支配人,
Jonkheer:オランダ貴族(男),
Mlle:マドモワゼル (フランス未婚女性),
Miss:未婚女性、女の子,
Mme:マダム(フランス既婚女性),
Ms:女性(未婚・既婚問わず),
Mrs:既婚女性,
Don:貴族や聖職者に使われる尊称,
Sir:男(イギリス)または伯爵,
the Countess:伯爵夫人,
Dona:既婚女性(スペイン),
Lady:既婚女性(イギリス),
Capt:船長,
Col:大佐,
Major:軍人,
Dr:医者,
Rev:聖職者や牧師
"""
df["HonorificsLabel"] = df["Honorifics"]
df['HonorificsLabel'].replace(['Mr'], 'Mr', inplace=True)
df['HonorificsLabel'].replace(['Ms', "Mlle", "Miss"], 'Miss', inplace=True)
df['HonorificsLabel'].replace(['Mme', 'Mrs'], 'Mrs', inplace=True)
df['HonorificsLabel'].replace(['Lady', 'Countess','Capt', 'Col', 'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare', inplace=True)
dummy_columns.append("HonorificsLabel")
kouho_columns.append("Family_label")
plot_count_category(df, "HonorificsLabel", "Survived")
次に思いつきで結婚しているかどうかで見てみました。
def MaryApply(data):
if data["Honorifics"] in ["Mlle", "Miss"]:
return 0
elif data['Honorifics'] in ["Mme", "Mrs", "the Countess", "Dona", "Lady"]:
return 1
else:
return -1
df["IsMary"] = df.apply(MaryApply, axis=1)
kouho_columns.append("IsMary")
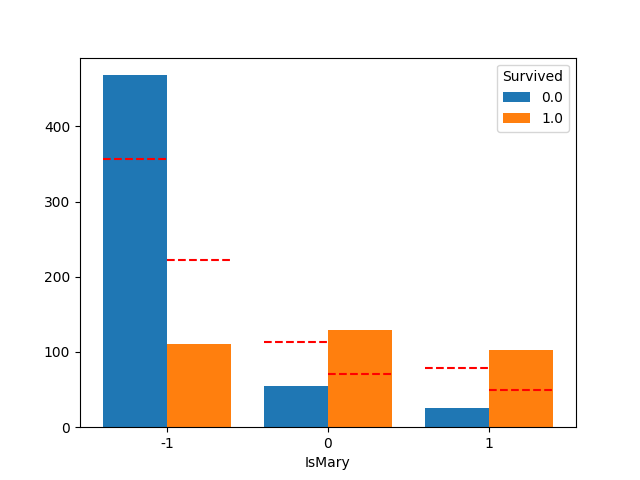
plot_count_category(df, "IsMary", "Survived")
不明な人が多くて役に立たなそうです。
# 評価
print(baseline_str)
valid_baseline_diff(df, [], [ "HonorificsLabel"], dummy_columns)
valid_baseline_diff(df, [], [ "IsMary"], dummy_columns)
metric: 0.78675645342312 (2):['Sex_female', 'Sex_male']
metric: 0.7934904601571269 (8):['HonorificsLabel_Master', ...]
metric: 0.78675645342312 (3):['IsMary', 'Sex_female', 'Sex_male']
敬称は効果がありそうですね。
1-9.Nameの分析 苗字 (新しい特徴量)
次は苗字に着目してみます。
苗字とPclass(チケットクラス)とEmbarked(乗船港)が同じ場合は家族としてカウントしてみます。
df['Surname'] = df['Name'].apply(lambda x:x.split(',')[0].strip())
df['Family_id'] = df['Surname'] + df["Pclass"].astype(str) + df["Embarked"]
Family_Count = dict(df['Family_id'].value_counts())
df['Family_count'] = df["Family_id"].apply(lambda x:Family_Count[x])
# 大人数の家族を見てみます。
for k in df[df["Family_count"] > 5]["Family_id"].unique():
# 見やすいように出力項目を決める
print(df[df["Family_id"]==k][["Pclass", "Sex", "Age", "Ticket", "Fare", "Embarked", "Cabin1_label", "FamilySize", "Honorifics", "Family_count"]].T)
break
8 172 302 597 719 869
Pclass 3 3 3 3 3 3
Sex female female male male male male
Age 27.0 1.0 19.0 49.0 33.0 4.0
Ticket 347742 347742 LINE LINE 347062 347742
Fare 11.1333 11.1333 0.0 0.0 7.775 11.1333
Embarked S S S S S S
Cabin1_label U U U U U U
FamilySize 3 3 1 1 1 3
Honorifics Mrs Miss Mr Mr Mr Master
Family_count 6 6 6 6 6 6
見てみるといくつか発見がありました。
- 同じTicketは同じ苗字の場合が多い、または同じチケットで苗字がバラバラ
- 同じチケットの値段(Fare)はほぼ同じ
- LINEというFareが0のチケットがある
まずはTicketとFareの関係を見てみます。
# 同じチケットでFareが違う人
for k in df["Ticket"].unique():
df2 = df[df["Ticket"]==k]
if df2["Fare"].min() != df2["Fare"].max():
print(df2.T)
※いらない情報は削除しています
138 876
Survived 0 0
Pclass 3 3
Sex male male
Age 16 20
Ticket 7534 7534
Fare 9.2167 9.8458
Fare_na 0 0
Cabin Unknown Unknown
Embarked S S
Fare_clip 9.2167 9.8458
FamilySize 1 1
Honorifics Mr Mr
IsRoyalty False False
Surname Osen Gustafsson
Family_id Osen3S Gustafsson3S
Family_count 1 4
2人しかいませんでした。(Fare_naが0なので、欠損値による影響というわけでもありません)
チケット番号毎にチケットは売られていると考えていいでしょう。
次にFareが0のTicketを見てみます。
print(df[df["Fare"]==0]["Ticket"].value_counts())
LINE 4
239853 3
112058 2
112059 1
112052 1
112050 1
112051 1
19972 1
239856 1
239855 1
239854 1
Name: Ticket, dtype: int64
いくつかあるようですね。
一応チケット人数毎の生存率も見ておきます。
Ticket_Count = dict(df['Ticket'].value_counts())
df['TicketSize'] = df["Ticket"].apply(lambda x:Ticket_Count[x])
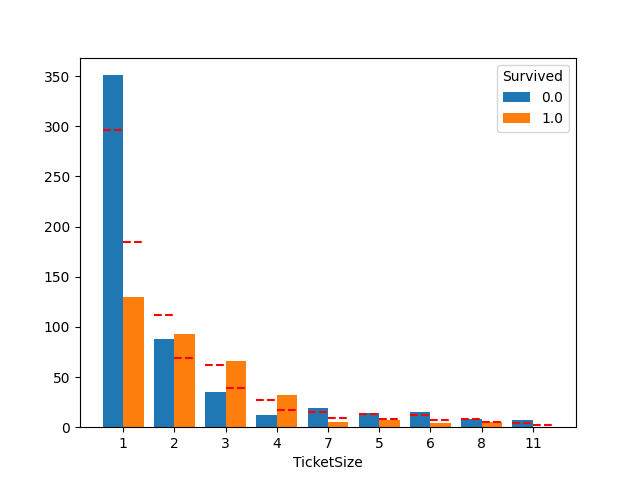
plot_count_category(df, "TicketSize", "Survived")
2~4人のグループで生存率が高く、FamilySize と似た傾向があります。
1-10.Age 年齢 (欠損値)
Age の欠損値を補完します。
Ageは回帰により予測します。
まずはどの変数がAgeに影響あるか見てみます。
# 比較するカラムを選択
df2 = df[[
"Age",
"Cabin_label",
"Cabin1_label",
"Cabin2_label",
"Cabin3_label",
"Cabin4_label",
"Embarked",
"Family_label",
"FamilySize",
"Family_count",
"Fare",
"HonorificsLabel",
"IsAlone",
"Parch",
"Pclass",
"Sex",
"SibSp",
"TicketSize",
]].copy()
# 正規化
df2["Fare"] = sklearn.preprocessing.StandardScaler().fit_transform(df2["Fare"].to_numpy().reshape((-1, 1)))
# ダミー化
df2 = pd.get_dummies(df2, columns=list(set(dummy_columns) & set(df2.columns)))
cr = compute_correlation_relationship(df2, df2.columns, "Age", pred_type="Regressor")
print(cr)
plot_category_bar(cr, "RandomForest")
plot_category_bar(cr, "OLS_val")
plot_category_bar(cr, "corr")
ざっくり以下の変数から予測します。
select_columns = ["Fare", "Pclass", "Cabin_label", "Parch", "SibSp"]
# ダミーカラム名を取得
select_columns = generate_to_dummy_name(df, select_columns, dummy_columns)
# 予測モデル
model_cls = sklearn.ensemble.RandomForestRegressor
params = {"random_state": SEED}
# 評価はRMSE
eval_func = lambda true_y, pred_y: np.sqrt(sklearn.metrics.mean_squared_error(true_y, pred_y))
# 評価・予測
# df2を引き続き使用
metric, pred_y = validation(df2, select_columns, "Age", model_cls, params, eval_func, is_pred=True)
print("RMSE: {} ({}){} ".format(metric, len(df.columns), df.columns))
# 予測結果を代入
df["Age_pred"] = df["Age"]
df.loc[df["Age_pred"].isnull(), "Age_pred"] = pred_y
kouho_columns.append("Age_pred")
# 中央値版も比較で作る
df["Age_na"] = df["Age"].isnull()
df["Age_med"] = df["Age"]
df["Age_med"].fillna(df["Age_med"].median(), inplace=True)
RMSE: 12.903842832611682 (31)Index(['PassengerId', ...
RMSEは単位がそのまま年齢になります。
なので13才ぐらい誤差がある予測結果です。
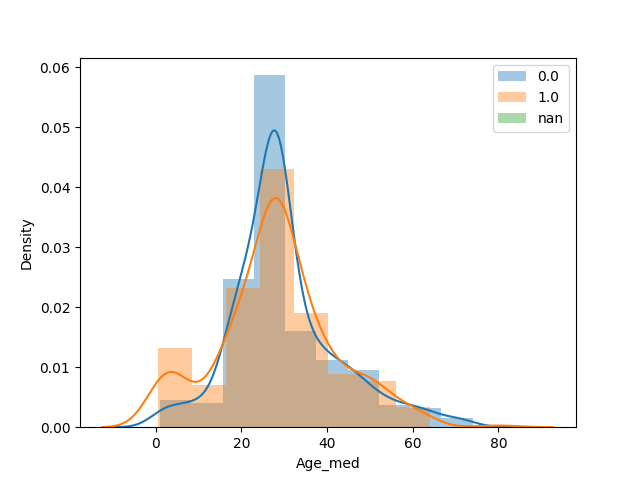
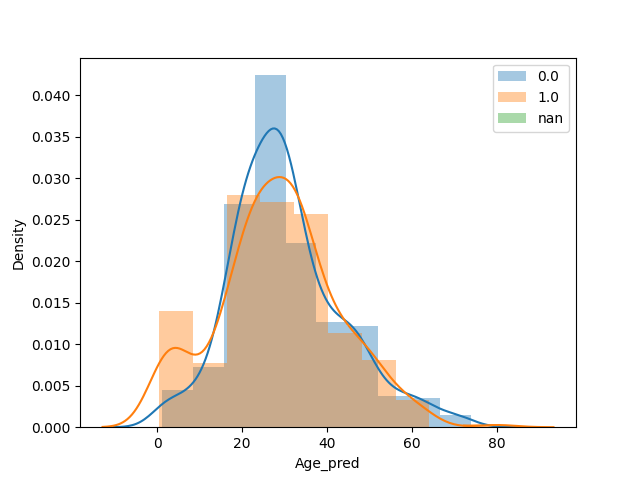
plot_float_category(df, "Age_med", "Survived")
plot_float_category(df, "Age_pred", "Survived")
少し自然な感じになったような?
評価も見てみます。
print(baseline_str)
valid_baseline_diff(df, [], [ "Age_med"], dummy_columns)
valid_baseline_diff(df, [], [ "Age_pred"], dummy_columns)
metric: 0.78675645342312 (2):['Sex_female', 'Sex_male']
metric: 0.7508417508417509 (3):['Age_med', 'Sex_female', 'Sex_male']
metric: 0.7609427609427609 (3):['Age_pred', 'Sex_female', 'Sex_male']
中央値よりは効果がありそうです。
2.特徴量抽出
今回作成した特徴量候補は以下です。
print(kouho_columns)
print(generate_to_dummy_name(df, kouho_columns, dummy_columns))
['Sex', 'Fare_label', 'Cabin_label', 'FamilySize', 'IsAlone', 'Family_label', 'HonorificsLabel', 'Age_pred']
['Sex_male', 'Sex_female', 'Fare_label_0', 'Fare_label_2', 'Fare_label_1', 'Cabin_label_U', 'Cabin_label_ABC', 'Cabin_label_DE', 'Cabin_label_FG', 'FamilySize', 'IsAlone', 'Family_label_1', 'Family_label_0', 'Family_label_2', 'HonorificsLabel_Mr', 'HonorificsLabel_Mrs', 'HonorificsLabel_Miss', 'HonorificsLabel_Master', 'HonorificsLabel_Rare', 'HonorificsLabel_the Countess', 'Age_pred']
この中から学習に使う特徴量を選びます。
参考: 特徴量選択のまとめ
いろいろありますが、今回は Forward Feature Selection (イテレーションごとに特徴量を1つずつ追加していく手法)を自作してみました。
# --- もう特徴量は追加しないのでダミー化します。
kouho_dummy_columns = generate_to_dummy_name(df, kouho_columns, dummy_columns)
df_dummy = pd.get_dummies(df, columns=list(set(dummy_columns) & set(kouho_columns)))
# ---------------------
# 評価モデル
model_cls = sklearn.ensemble.RandomForestClassifier
model_params = {"random_state": SEED}
# 評価は正解率
eval_func = lambda true_y, pred_y: sklearn.metrics.accuracy_score(true_y, pred_y)
# --- ここから探索
choice_columns = []
base_metric = 0
for _ in range(len(kouho_dummy_columns)):
# 全カラムを評価し、一番いい評価のカラムを特徴量として追加していく
metrics = []
for column in tqdm(kouho_dummy_columns):
if column in choice_columns:
continue
_c = choice_columns[:]
_c.append(column)
metric = validation(df_dummy, _c, "Survived", model_cls, model_params, eval_func)
metrics.append((column, metric))
# 最大評価を追加する、評価が更新できなかったらその時点で終了
metrics.sort(key=lambda x:x[1], reverse=True)
max_metric = metrics[0]
if base_metric < max_metric[1]:
base_metric = max_metric[1]
choice_columns.append(max_metric[0])
else:
break
# 結果
print(choice_columns)
['Sex_male', 'Family_label_2', 'Pclass_3', 'Fare_label_2', 'Embarked_S', 'IsMary']
まさかの適当に追加した IsMary が残ったのは意外でした。
3.ハイパーパラメータの調整
機械学習はハイパーパラメータにかなり敏感です。
今回はOptunaで調整してみました。
# 調整するハイパーパラメータを定義
def objective(trial):
# モデル
model_cls = sklearn.ensemble.RandomForestClassifier
model_params = {
"n_estimators": trial.suggest_int('n_estimators', 50, 1000),
"criterion": trial.suggest_categorical('criterion', ["gini", "entropy"]),
"max_depth": trial.suggest_int('max_depth', 1, 100),
"random_state": SEED,
}
# 評価方法
eval_func = lambda true_y, pred_y: sklearn.metrics.accuracy_score(true_y, pred_y)
# 評価
metric = validation(df_dummy, choice_columns, "Survived", model_cls, model_params, eval_func)
return metric
# 最大化で調整開始
study = optuna.create_study(direction="maximize")
study.optimize(objective, n_trials=100)
# optunaの結果を取得
print(study.best_params)
print(study.best_value)
model_params = study.best_params
{'n_estimators': 143, 'criterion': 'entropy', 'max_depth': 29}
0.8193041526374859
4.提出
# モデル
model_params = study.best_params
model_params["random_state"] = SEED
model_cls = sklearn.ensemble.RandomForestClassifier
# 評価方法
eval_func = lambda true_y, pred_y: sklearn.metrics.accuracy_score(true_y, pred_y)
# 予測+評価
metrics, pred_y = validation(df_dummy, choice_columns, "Survived", model_cls, params, eval_func, is_pred=True)
print(metrics)
# 整数に直す
pred_y = pred_y.astype(np.int64)
# 提出用にデータ加工
output = pd.DataFrame({'PassengerId': df_test["PassengerId"], 'Survived': pred_y})
output.to_csv("result.csv", header=True, index=False)
print("Your submission was successfully saved!")
0.8193041526374859
Your submission was successfully saved!
提出スコアは 0.77990 でした。
あとがき
まだ抜き出せる特徴量はたくさんありますが、きりがないのでここで一区切りです。
スコアは全然上がりませんでしたね。(一応女性だけのスコアを超えたのでよしとします)
ただ特徴量に対する分析はなんとなくわかった気がします。
タイタニックはこれでいったん終わりです。