はじめに
最近データサイエンスに関して勉強する機会があったので覚えた技術を忘れないように記事に書いておきます。
対象の事例としてKaggleチュートリアルのタイタニックを使います。
Kaggleみたいなちゃんとしたデータセットでデータ分析するのは初めてなので間違っている点は多々あると思います。
・Kaggle関係の記事
Kaggleのタイタニックに挑戦してみた(その1)(ここ)
Kaggleのタイタニックに挑戦してみた(その2)
Kaggleで書いたコードの備忘録その1~データ分析で使った手法一通り~
Kaggleで書いたコードの備忘録その2~自然言語処理まとめ~
KaggleタイタニックでNameだけで予測精度80%超えた話(BERT)
コード全体
作成したコードは以下です。
1.データの確認
タイタニックのデータセットは、各乗客の情報を元に生き残ったかどうかを学習するデータセットです。
以下の3個のファイルが提供されています。
- train.csv:学習用データ
- test.csv:予測データ
- gender_submission.csv:提出例
"gender_submission.csv" は女性=生存、男性=死亡で予測したファイルで、これを提出するとスコアは 0.76555 になります。(パーセントなので正解率77%ですね)
まずは、train.csv にどんなデータが入っているか確認してみます。
データの読み込みは以下です。
import pandas as pd
from matplotlib import pyplot as plt # グラフ表示用
import seaborn as sns # グラフ表示用
df_train = pd.read_csv(os.path.join(os.path.dirname(__file__), "./titanic/train.csv"))
df_test = pd.read_csv(os.path.join(os.path.dirname(__file__), "./titanic/test.csv"))
target_column = "Survived" # 目的変数
random_seed = 1234 # 乱数固定用
1-1.カラム一覧と欠損値の確認
まずはどんなカラムがあるかと欠損値を確認します。
# 総データ数
print(len(df_train))
print(len(df_test))
# 欠損値の数を表示
print(df_train.isnull().sum())
print(df_test.isnull().sum())
- 表示結果
891 # trainデータ数
418 # testデータ数
# train
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64
# test
PassengerId 0
Pclass 0
Name 0
Sex 0
Age 86
SibSp 0
Parch 0
Ticket 0
Fare 1
Cabin 327
Embarked 0
dtype: int64
AgeとCabinはやたら欠損値が多いですね。
Embarked と Fare の欠損値は数が少ないのでデータを見てもいいかもしれません。
# Fareのデータを見る例
print(df_test[df_test["Fare"].isnull()].T) # .Tは記事として見やすいように転置
# 出力結果
152
PassengerId 1044
Pclass 3
Name Storey, Mr. Thomas
Sex male
Age 60.5
SibSp 0
Parch 0
Ticket 3701
Fare NaN
Cabin NaN
Embarked S
1-2.各カラムの要約情報の確認
どういうデータが入っているか確認してみます。
# 要約情報
print(df_train.describe(include='all'))
print(df_test.describe(include='all'))
記事だと見づらくなるので表示は一部のみにしています。
print(df_train[["PassengerId", "Pclass", "Sex", "Age"]].describe(include='all'))
PassengerId Pclass Sex Age
count 891.000000 891.000000 891 714.000000
unique NaN NaN 2 NaN
top NaN NaN male NaN
freq NaN NaN 577 NaN
mean 446.000000 2.308642 NaN 29.699118
std 257.353842 0.836071 NaN 14.526497
min 1.000000 1.000000 NaN 0.420000
25% 223.500000 2.000000 NaN 20.125000
50% 446.000000 3.000000 NaN 28.000000
75% 668.500000 3.000000 NaN 38.000000
max 891.000000 3.000000 NaN 80.000000
なんとなく確認した箇所は以下です。
- (数字データ)外れ値がないか(meanに対するminとmaxらへんを確認)
- (数字データ)データの散らばり具合(meanに対する50%(中央値)がどれだけ離れているか)
- (文字データ)カテゴリデータかどうか(countとuniqueの数)
また合わせてuniqueな要素についても詳細を見ておきます。
for column in df_train.columns:
# uniq情報を取得
uniq = df_train[column].unique()
# 表示
print("{:20} unique:{:5} {}".format(
column,
len(uniq),
uniq[:5], # 多すぎる場合があるので5件に抑える
))
PassengerId unique: 891 [1 2 3 4 5]
Survived unique: 2 [0 1]
Pclass unique: 3 [3 1 2]
Name unique: 891 ['Braund, Mr. Owen Harris'
'Cumings, Mrs. John Bradley (Florence Briggs Thayer)'
'Heikkinen, Miss. Laina' 'Futrelle, Mrs. Jacques Heath (Lily May Peel)'
'Allen, Mr. William Henry']
Sex unique: 2 ['male' 'female']
Age unique: 89 [22. 38. 26. 35. nan]
SibSp unique: 7 [1 0 3 4 2]
Parch unique: 7 [0 1 2 5 3]
Ticket unique: 681 ['A/5 21171' 'PC 17599' 'STON/O2. 3101282' '113803' '373450']
Fare unique: 248 [ 7.25 71.2833 7.925 53.1 8.05 ]
Cabin unique: 148 [nan 'C85' 'C123' 'E46' 'G6']
Embarked unique: 4 ['S' 'C' 'Q' nan]
ここで確認したい点はunique数です。
count数とunique数が同じ場合は各データを区別するユニークIDな意味合いが強く、unique数が少ない場合はカテゴリなデータの可能性が高くなります。
ドメイン知識なしで各カラムを見た場合をまとめてみました。
| カラム名 | 予測データ形式 | どんなデータ? |
|---|---|---|
| PassengerId | ID | count数=unique数なのでIDっぽい |
| Survived | 目的変数です。(生存したか)(これだけドメイン知識あり) | |
| Pclass | カテゴリ | unique 3なのでカテゴリっぽい(intなので数字で分類していそう) |
| Name | ID | count数=unique数なのでIDっぽい |
| Sex | カテゴリ | unique 2、データタイプが文字列なのでカテゴリ |
| Age | 小数 | 平均29で中央値28とばらつきはなさそう |
| SibSp | カテゴリ? | unique 7と少し多いのでカテゴリかどうかは微妙 |
| Parch | カテゴリ? | unique 7と少し多いのでカテゴリかどうかは微妙 |
| Ticket | ? | unique 681 と全部違うわけでもない…。よくわからないですね |
| Fare | 小数 | 平均35、中央値31に対してmaxが512なので外れ値があるかも? |
| Cabin | ? | 欠損値が多く、unique 148とかなりバラバラ |
| Embarked | カテゴリ | unique 4、データタイプが文字列なのでカテゴリ |
1-3.各カラムと目的変数との関係
各カラムに対して目的変数との関係を見てみます。
カラムはすべて見るわけではなく、上記まとめから気になった項目のみ見ています。
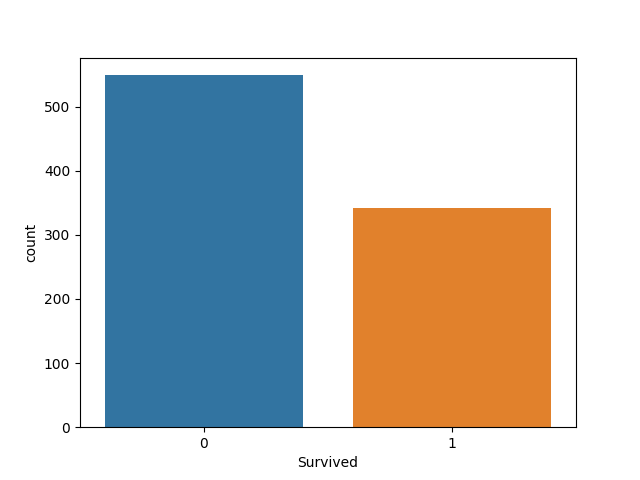
Survived
まずは目的変数です。
print(df_train['Survived'].value_counts()) # 数
print(df_train['Survived'].value_counts(normalize=True)) # 割合
sns.countplot(x="Survived", data=df_train)
plt.show()
0 549
1 342
Name: Survived, dtype: int64
0 0.616162
1 0.383838
Name: Survived, dtype: float64
カテゴリ系の表示
カテゴリ系は以下のようなコードで表示しています。(Pclassの例)
def plot_category(df, column, target_column):
# カウント情報
print(pd.crosstab(df[column],df[target_column]))
print("各クラス毎の生存率")
print(pd.crosstab(df[column],df[target_column], normalize='index'))
print("生存率に対する各クラスの割合")
print(pd.crosstab(df[column],df[target_column], normalize='columns'))
# plot
sns.countplot(df[column], hue=df[target_column])
plt.show()
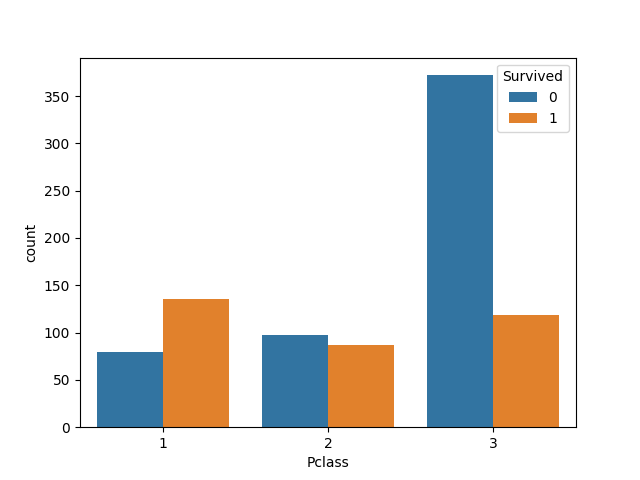
plot_count(df_train, "Pclass", "Survived")
Survived 0 1
Pclass
1 80 136
2 97 87
3 372 119
各クラス毎の生存率
Survived 0 1
Pclass
1 0.370370 0.629630
2 0.527174 0.472826
3 0.757637 0.242363
生存率に対する各クラスの割合
Survived 0 1
Pclass
1 0.145719 0.397661
2 0.176685 0.254386
3 0.677596 0.347953
以下画像のみ表示します。
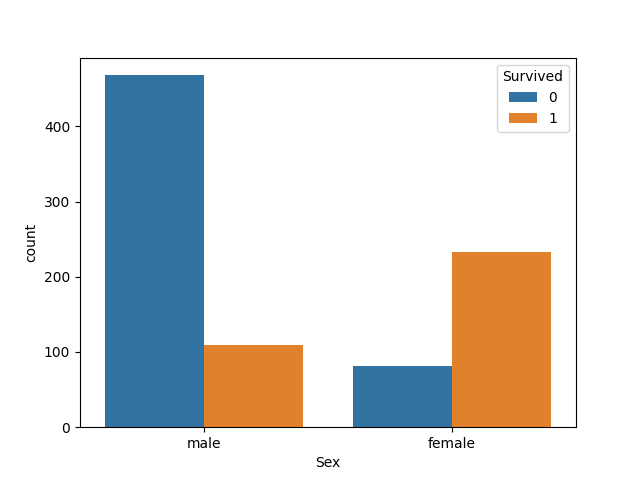
- Sex
男性の死亡率、女性の生存率がかなり高いですね。
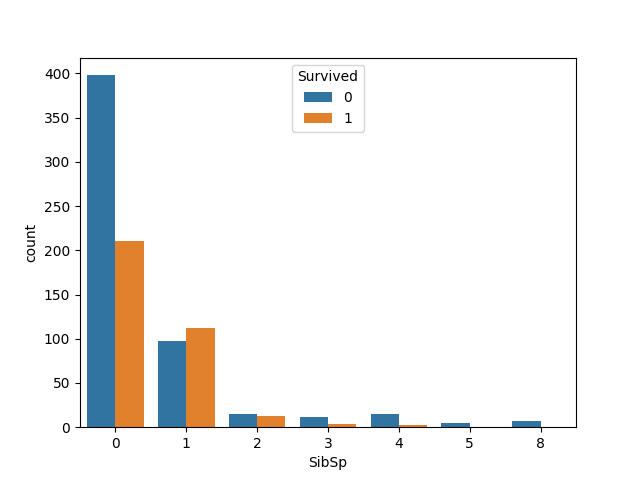
- SibSp
0と1がほとんどの割合を占めていますね。
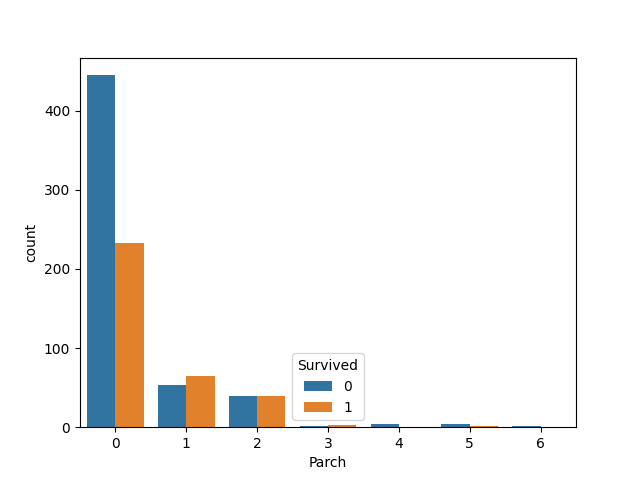
- Parch
同じく、0,1,2がほとんどの割合を占めていますね。
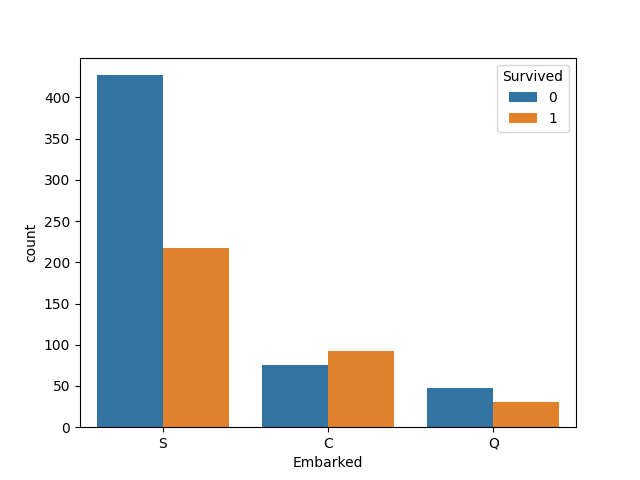
- Embarked
Sが多いですね。
小数系データの表示
ヒストグラムを表示しています。
なんとなく全体のヒストグラムと生存者毎のヒストグラムを表示しています。
def plot_float(df, column, target_column, bins=20):
# 全体plot
sns.distplot(df[column], kde=True, rug=False, bins=bins)
plt.show()
# 目的変数毎のplot
sns.distplot(df[df[target_column]==1][column], kde=True, rug=False, bins=bins, label=1)
sns.distplot(df[df[target_column]==0][column], kde=True, rug=False, bins=bins, label=0)
plt.legend()
plt.show()
# Age出力例
plot_float(df_train, "Age", target_name)
kdeはカーネル密度推定というものらしく、ざっくりいうとヒストグラムを連続値にした場合のグラフです。
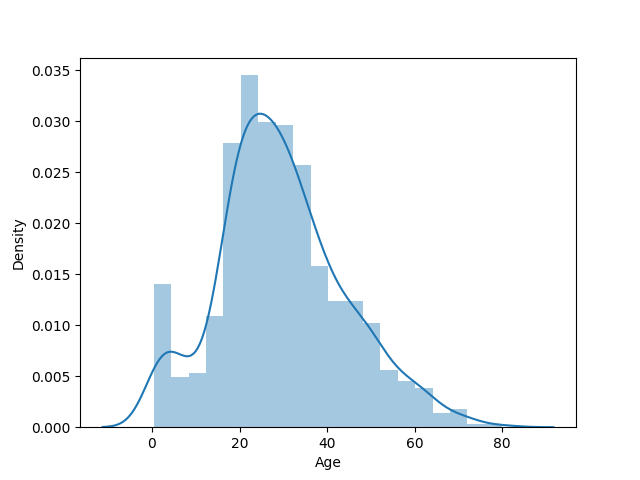
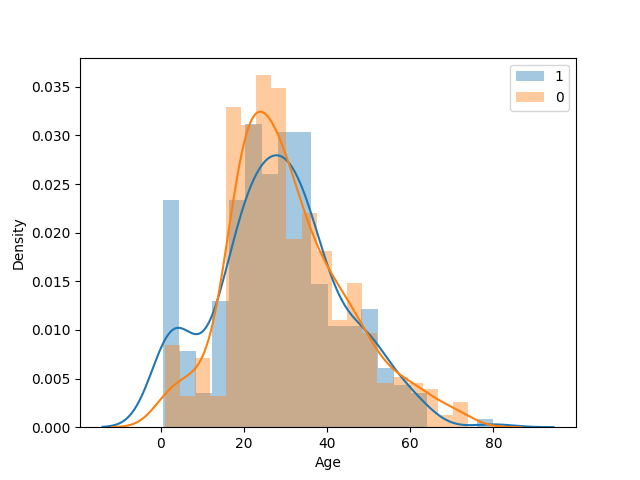
- Age
10才以下あたりで生存率が高い点が気になりますね。
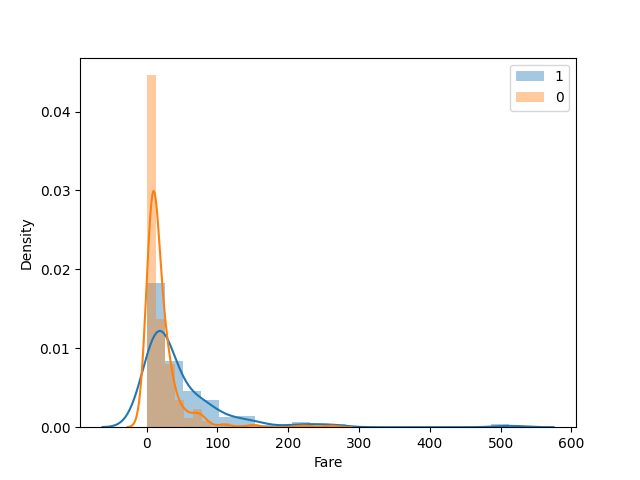
- Fare
生存率毎のグラフのみ表示しています。
低いと死亡率が高く、高いと死亡率が低そうです。
2.学習データの作成(前処理)
データが確認できたので次は学習用データを作成します。
まずは最低限の処理のみを実装し、改善は後回しにします。(とりあえず一連のフローを作ることを優先しています)
また、この最低限の状態のスコアをベースとすることで改善されているかを比較する目的もあります。
2-1.欠損値の補填
欠損値の埋め方は、平均値や中央値がよく使われるようです。
また、Cabinは欠損値の割合が多いので今回は説明変数に含めない方向で対処します。
- Age
とりあえず中央値で埋めます。
また、欠損値を埋めたことを表すフラグを新規に作っています。
def missing_value(df):
# 欠損値フラグ
df["Age_na"] = df["Age"].isnull().astype(np.int64)
# 欠損値を中央値で埋める
df["Age"].fillna(df["Age"].median(), inplace=True)
missing_value(df_train) # trainデータ
missing_value(df_test) # testデータ
- Embarked
2件だけですので一番多かった S で補完します。
df_train["Embarked"].fillna("S", inplace=True)
- Fare
こちらも1件だけですので中央値で補完します。
df_test["Fare"].fillna(df_test['Fare'].median(), inplace=True)
2-2.(正規化)
データの単位を揃えて学習しやすくする方法です。
今回は正規化しませんがコードのみ書いておきます。
def normalization(df, name):
# 正規化(不偏分散)
df[name] = (df[name] - df[name].mean()) / df[name].std()
# normalization(df_train, "Age")
# normalization(df_train, "Fare")
# normalization(df_test, "Age")
# normalization(df_test, "Fare")
2-3.ダミー化
カテゴリなカラムに対してカテゴリ別にカラムを増やします。
(Onehot化と同じ変換です)
例えば以下の表をダミー化すると以下になります。
| Sex | |
|---|---|
| 1 | male |
| 2 | female |
| 3 | male |
↓ ダミー化
| Sex_male | Sex_female | |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
SibSpとParchのダミー化はとりあえずおいておきます。
def dummy(df):
df = pd.get_dummies(df, columns=[
"Pclass",
"Sex",
#"SibSp",
#"Parch",
"Embarked",
])
return df
df_train = dummy(df_train)
df_test = dummy(df_test)
2-4.説明変数の選択
ここまで実行した後のカラムは以下です。
print(list(df_train.columns))
# ['PassengerId', 'Survived', 'Name', 'Age', 'SibSp', 'Parch', 'Ticket', 'Fare', 'Cabin', 'Age_na', 'Pclass_1', 'Pclass_2', 'Pclass_3', 'Sex_female', 'Sex_male', 'Embarked_C', 'Embarked_Q', 'Embarked_S']
この中から実際に学習で使う説明変数を選択します。
とりあえずデータが数字で表されている要素をすべて使ってみます。
またDummy化した変数ですが、1つだけは情報がかぶっており不要なので最後のDummy変数を除外しておきます。
select_columns = [
"Age",
"Age_na",
"SibSp",
"Parch",
"Fare",
"Pclass_1",
"Pclass_2",
#"Pclass_3", # dummy除外
"Sex_male",
#"Sex_female", # dummy除外
"Embarked_C",
"Embarked_Q",
#"Embarked_S", # dummy除外
]
3.ローカルで学習
まずはローカルで学習して評価してみます。
今後変わるかもしれませんが、今回は以下の方針で学習してみます。
- 複数のモデルで性能を比較(前処理方法の妥当性検証がメインになりそうなので)
- 交差検証で検証(未知のデータの正答率を上げたいので、複数の学習パターンで学習し平均をとる)
3-1.学習モデル
複数のモデルで比較しています。
モデルは参考のサイトから持ってきています。
参考:クレジットカード不正利用予測モデルを作成・評価してみた
import sklearn.ensemble
import sklearn.gaussian_process
import sklearn.naive_bayes
import sklearn.linear_model
import sklearn.neighbors
import sklearn.tree
import sklearn.discriminant_analysis
import xgboost as xgb
import lightgbm as lgb
def create_models(random_seed):
models = [
#Ensemble Methods
sklearn.ensemble.AdaBoostClassifier(random_state=random_seed),
sklearn.ensemble.BaggingClassifier(random_state=random_seed),
sklearn.ensemble.ExtraTreesClassifier(random_state=random_seed),
sklearn.ensemble.GradientBoostingClassifier(random_state=random_seed),
sklearn.ensemble.RandomForestClassifier(random_state=random_seed),
#Gaussian Processes
sklearn.gaussian_process.GaussianProcessClassifier(random_state=random_seed),
#GLM
sklearn.linear_model.LogisticRegressionCV(random_state=random_seed),
sklearn.linear_model.RidgeClassifierCV(),
#Navies Bayes
sklearn.naive_bayes.BernoulliNB(),
sklearn.naive_bayes.GaussianNB(),
#Nearest Neighbor
sklearn.neighbors.KNeighborsClassifier(),
#Trees
sklearn.tree.DecisionTreeClassifier(random_state=random_seed),
sklearn.tree.ExtraTreeClassifier(random_state=random_seed),
#Discriminant Analysis
sklearn.discriminant_analysis.LinearDiscriminantAnalysis(),
sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis(),
#xgboost
xgb.XGBClassifier(eval_metric="logloss", use_label_encoder=False, random_state=random_seed),
# light bgm
lgb.LGBMClassifier(random_state=random_seed),
]
return models
3-2.(サンプリング)
目的変数のデータに差がある場合データ数を調整します。(いわゆる不均衡データ)
Survived の個数を見てみます。
sns.countplot(x="Survived", data=df_train)
plt.show()
死亡者の人数が多いのでアンダーサンプリング(死亡者の人数を減らして数を合わせる)してもいい気はしますが、今回は何もしません。
3-3.k-分割交差検証
k-分割交差検証(KFold)はデータをk個に分割し、k-1個のデータを学習用、1個のデータを検証用にして学習する方法です。
評価は正解率、適合率、再現率、F値とすべて見てみました。
コードは以下です。
def fit(df, columns, target_column, random_seed):
# 教師データを作成
x = df[columns].to_numpy()
y = df[target_name].to_numpy()
# 交叉検証
model_scores = {}
kf = sklearn.model_selection.KFold(n_splits=3, shuffle=True, random_state=random_seed)
for train_idx, true_idx in kf.split(x, y):
# 各学習データとテストデータ
x_train = x[train_idx]
y_train = y[train_idx]
x_true = x[true_idx]
y_true = y[true_idx]
# 各モデル毎に学習
for model in create_models(random_seed):
name = model.__class__.__name__
if name not in model_scores:
model_scores[name] = []
# モデルの学習と評価
model.fit(x_train, y_train)
pred_y = model.predict(x_true)
# 結果を評価
model_scores[name].append((
sklearn.metrics.accuracy_score(y_true, pred_y),
sklearn.metrics.precision_score(y_true, pred_y),
sklearn.metrics.recall_score(y_true, pred_y),
sklearn.metrics.f1_score(y_true, pred_y),
))
accs = []
for k, scores in model_scores.items():
scores = np.mean(scores, axis=0)
# モデル毎の平均
print("正解率 {:.3f}, 適合率 {:.3f}, 再現率 {:.3f}, F値 {:.3f} : {}".format(
scores[0],
scores[1],
scores[2],
scores[3],
k,
))
accs.append(scores)
# 全モデルの中央値
accs = np.median(accs, axis=0) # 中央値
print("正解率 {:.3f}, 適合率 {:.3f}, 再現率 {:.3f}, F値 {:.3f}".format(accs[0], accs[1], accs[2], accs[3]))
# 実行
fit(df_train, select_columns, target_column, random_seed)
実行結果
正解率 0.806, 適合率 0.762, 再現率 0.720, F値 0.740 : AdaBoostClassifier
正解率 0.811, 適合率 0.786, 再現率 0.699, F値 0.740 : BaggingClassifier
正解率 0.801, 適合率 0.743, 再現率 0.737, F値 0.740 : ExtraTreesClassifier
正解率 0.818, 適合率 0.796, 再現率 0.708, F値 0.749 : GradientBoostingClassifier
正解率 0.807, 適合率 0.764, 再現率 0.720, F値 0.741 : RandomForestClassifier
正解率 0.707, 適合率 0.639, 再現率 0.547, F値 0.589 : GaussianProcessClassifier
正解率 0.805, 適合率 0.782, 再現率 0.684, F値 0.729 : LogisticRegressionCV
正解率 0.799, 適合率 0.767, 再現率 0.687, F値 0.724 : RidgeClassifierCV
正解率 0.774, 適合率 0.711, 再現率 0.696, F値 0.703 : BernoulliNB
正解率 0.774, 適合率 0.722, 再現率 0.673, F値 0.696 : GaussianNB
正解率 0.686, 適合率 0.600, 再現率 0.531, F値 0.564 : KNeighborsClassifier
正解率 0.773, 適合率 0.699, 再現率 0.719, F値 0.709 : DecisionTreeClassifier
正解率 0.777, 適合率 0.718, 再現率 0.690, F値 0.704 : ExtraTreeClassifier
正解率 0.799, 適合率 0.767, 再現率 0.687, F値 0.724 : LinearDiscriminantAnalysis
正解率 0.800, 適合率 0.763, 再現率 0.698, F値 0.728 : QuadraticDiscriminantAnalysis
正解率 0.817, 適合率 0.783, 再現率 0.726, F値 0.753 : XGBClassifier
正解率 0.824, 適合率 0.796, 再現率 0.728, F値 0.760 : LGBMClassifier
正解率 0.800, 適合率 0.763, 再現率 0.698, F値 0.728
モデル全て見る必要はなさそうですね。
最後の行が全モデルの中央値になり、これだけ見ればよさそうです。
最初から正解率80%とかなり高い結果になりましたね…。
4.提出用データの学習
提出用データはとりあえずランダムフォレストを採用してハイパーパラメータはデフォルトのままでいきます。
4-1.(ハイパーパラメータの調整)
ハイパーパラメータの調整ですが、今回は実施しません。
まだモデルが決まっていないのと調整に時間がかかりそうなので、前処理の方針が決まった後に実施する予定です。
4-2.ランダムフォレスト
学習コードです。
# 学習データを作成
x = df_train[select_columns].to_numpy()
y = df_train[target_column].to_numpy()
# 出力用データ
x_test = df_test[select_columns].to_numpy()
# ランダムフォレストで学習し、評価する
model = sklearn.ensemble.RandomForestClassifier(random_state=random_seed)
model.fit(x, y)
pred_y = model.predict(x_test)
# 提出用にデータ加工
output = pd.DataFrame({'PassengerId': df_test["PassengerId"], 'Survived': pred_y})
output.to_csv("result.csv", header=True, index=False)
print("Your submission was successfully saved!")
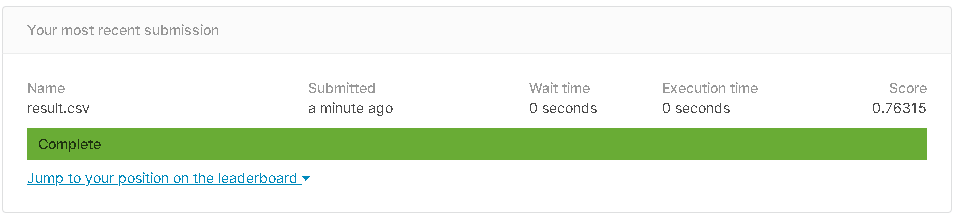
提出結果
結果は 0.76315 でした。
gender_submission.csv より低いですね…
5.その他の分析
ここまでで一連の流れはできましたが、説明変数に対してもうちょっと分析手法を取り入れてみます。
5-1.説明変数の影響度
いくつかのモデルは説明変数に対して目的変数をどの程度説明できているかを見ることができます。
RandomForestClassifier と XGBClassifier と LGBMClassifier で見てみます。
def print_feature_importance(df, columns, target_column, random_seed):
x = df[columns]
y = df[target_column]
print("--- RandomForestClassifier")
model = sklearn.ensemble.RandomForestClassifier(random_state=random_seed)
model.fit(x, y)
fti1 = model.feature_importances_
for i, column in enumerate(columns):
print('{:20s} : {:>.6f}'.format(column, fti1[i]))
print("--- XGBClassifier")
model = xgb.XGBClassifier(eval_metric="logloss", use_label_encoder=False)
model.fit(x, y)
fti2 = model.feature_importances_
for i, column in enumerate(columns):
print('{:20s} : {:>.6f}'.format(column, fti2[i]))
print("--- LGBMClassifier")
model = lgb.LGBMClassifier(random_state=random_seed)
model.fit(x, y)
fti3 = model.feature_importances_
for i, column in enumerate(columns):
print('{:20s} : {:>.2f}'.format(column, fti3[i]))
#--- 結果をplot
fig = plt.figure()
ax1 = fig.add_subplot(3, 1, 1, title="RandomForestClassifier(Feature Importance)")
ax2 = fig.add_subplot(3, 1, 2, title="XGBClassifier(Feature Importance)")
ax3 = fig.add_subplot(3, 1, 3, title="LGBMClassifier(Feature Importance)")
ax1.barh(columns, fti1)
ax2.barh(columns, fti2)
ax3.barh(columns, fti3)
fig.tight_layout()
plt.show()
# 実行
print_feature_importance(df_train, select_columns, target_column, random_seed)
実行結果
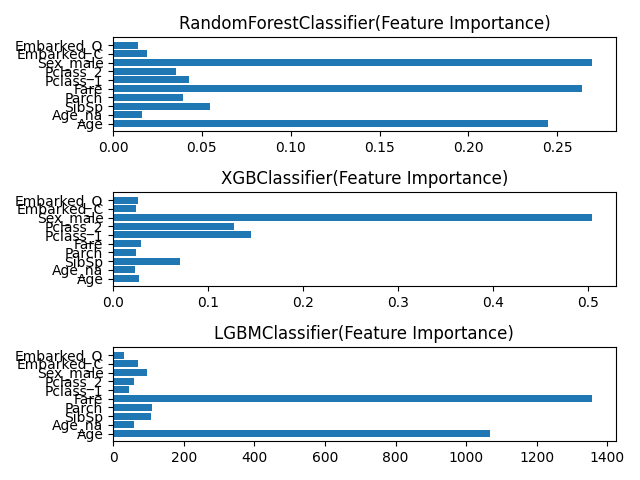
--- RandomForestClassifier
Age : 0.244622
Age_na : 0.016238
SibSp : 0.054778
Parch : 0.039426
Fare : 0.264062
Pclass_1 : 0.042784
Pclass_2 : 0.035545
Sex_male : 0.269452
Embarked_C : 0.019326
Embarked_Q : 0.013766
--- XGBClassifier
Age : 0.026774
Age_na : 0.022875
SibSp : 0.070061
Parch : 0.023662
Fare : 0.029577
Pclass_1 : 0.145431
Pclass_2 : 0.127607
Sex_male : 0.503674
Embarked_C : 0.023957
Embarked_Q : 0.026382
--- LGBMClassifier
Age : 1069.00
Age_na : 59.00
SibSp : 106.00
Parch : 109.00
Fare : 1356.00
Pclass_1 : 44.00
Pclass_2 : 58.00
Sex_male : 97.00
Embarked_C : 70.00
Embarked_Q : 31.00
Sex,Fare,Age が高い値をだしていますね。
割と重要(生存率にかなり影響がある)ようです。
5-2.回帰分析
回帰分析による分析結果を乗せます。
回帰分析では各説明変数の重要度だけではなく外れ値かどうかも見ることができます。
from statsmodels.stats.outliers_influence import OLSInfluence
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.api as sm
def print_statsmodels(df, columns, target_column):
# 重回帰分析
X1_train = sm.add_constant(df[columns])
y = df[target_column]
model = sm.OLS(y, X1_train)
fitted = model.fit()
# summary見方の参考
# https://self-development.info/%E3%80%90%E5%88%9D%E5%BF%83%E8%80%85%E8%84%B1%E5%87%BA%E3%80%91statsmodels%E3%81%AB%E3%82%88%E3%82%8B%E9%87%8D%E5%9B%9E%E5%B8%B0%E5%88%86%E6%9E%90%E7%B5%90%E6%9E%9C%E3%81%AE%E8%A6%8B%E6%96%B9/
#print('summary = \n', fitted.summary())
print("--- 重回帰分析の決定係数")
for i, column in enumerate(columns):
print('\t{:15s} : {:7.4f}(coef) {:5.1f}%(P>|t|)'.format(
column,
fitted.params[i+1],
fitted.pvalues[i]*100
))
print("")
# 各columnにおけるクック距離をだす
print("--- 外れ値(cook_distance threshold:0.5)")
for column in columns:
# 単回帰分析
X1_train = sm.add_constant(df[column])
model = sm.OLS(y, X1_train)
fitted = model.fit()
cook_distance, p_value = OLSInfluence(fitted).cooks_distance
kouho = np.where(cook_distance > 0.5)[0]
if len(kouho) == 0:
print("{:20s} cook_distance is 0(max: {:.4f})".format(column, np.max(cook_distance)))
else:
for index in kouho:
print("{:20s} cook_distance: {}, index: {}".format(column, cook_distance[index], index))
print("")
# 実行
print_statsmodels(df_train, select_columns, target_column)
重回帰分析
--- 重回帰分析の回帰係数(P値:5%以上の場合は結果が怪しい)
Age : -0.0058(coef) 0.0%(P>|t|)
Age_na : -0.0456(coef) 0.0%(P>|t|)
SibSp : -0.0399(coef) 19.0%(P>|t|)
Parch : -0.0186(coef) 0.2%(P>|t|)
Fare : 0.0003(coef) 31.0%(P>|t|)
Pclass_1 : 0.3328(coef) 32.3%(P>|t|)
Pclass_2 : 0.1852(coef) 0.0%(P>|t|)
Sex_male : -0.5023(coef) 0.0%(P>|t|)
Embarked_C : 0.0718(coef) 0.0%(P>|t|)
Embarked_Q : 0.0827(coef) 4.1%(P>|t|)
出力を分けています。
まずは重回帰分析時の結果ですが、各説明変数の回帰係数(coef)は5-1.の影響度と同じく、目的変数にどれだけ影響があるかの度合いになります。
またP値(有意確率)ですが、低いと有意性が高いと言えます。
0.05以上になると有意性が低くなり、回帰係数が実際には0の可能性があります。(P値はなかなか難しい話なので間違った言い回しになっているかも)
今回ですと、SibSp,Fare,Pclass_1,Embarked_QはP値が高いので外したほうが良いかもしれません。
また、回帰係数では Sex_male が高いので性別は影響度が高そうなことが分かります。
クックの距離
クックの距離ですが、簡単に言うと回帰分析において各データがどれだけ回帰係数に影響あるかを表した指標となります。
影響度が大きいデータは外れ値と考えることもできます。(あくまで回帰分析における影響度です)
コードは全説明変数に対して(重回帰分析)でクックの距離を出してしまうとど説明変数の影響かが分からないので、各説明変数に対して(単回帰分析)結果を出しています。
--- 外れ値(cook_distance threshold:0.1)
Age cook_distance is 0(max: 0.0217)
Age_na cook_distance is 0(max: 0.0061)
SibSp cook_distance is 0(max: 0.0120)
Parch cook_distance is 0(max: 0.0579)
Fare cook_distance: 0.10554792163598595, index: 258
Fare cook_distance: 0.10554792163598595, index: 679
Fare cook_distance: 0.10554792163598595, index: 737
Pclass_1 cook_distance is 0(max: 0.0043)
Pclass_2 cook_distance is 0(max: 0.0032)
Sex_male cook_distance is 0(max: 0.0053)
Embarked_C cook_distance is 0(max: 0.0040)
Embarked_Q cook_distance is 0(max: 0.0105)
閾値は正直よくわかっていません。
今回ですと、Fare に対してクックの距離0.1を超えるデータが3個ありました。
5-3.説明変数同士の相関
説明変数同士に強い相関がある場合、片方だけを採用すればよくなります。
その相関を見てみました。
コードは以下です。
def print_correlation(df, columns):
# 相関係数1:1
print("--- 相関係数1:1 (threshold: 0.5)")
cor = df[columns].corr()
count = 0
for i in range(len(columns)):
for j in range(i+1, len(columns)):
val = cor[columns[i]][j]
if abs(val) > 0.5:
print("{} {}: {:.2f}".format(columns[i], columns[j], val))
count += 1
if count == 0:
print("empty")
print("")
# heatmap
plt.figure(figsize=(12,9))
sns.heatmap(df[columns].corr(), annot=True, vmax=1, vmin=-1, fmt='.1f', cmap='RdBu')
plt.show()
# 相関係数1:多
# 5以上だとあやしい、10だとかなり確定
print("--- VIF(5以上だと怪しい)")
vif = pd.DataFrame()
x = df[columns]
vif["VIF Factor"] = [
variance_inflation_factor(x.values, i) for i in range(x.shape[1])
]
vif["features"] = columns
print(vif)
plt.barh(columns, vif["VIF Factor"])
plt.vlines([5], 0, len(columns), "blue", linestyles='dashed')
plt.vlines([10], 0, len(columns), "red", linestyles='dashed')
plt.title("VIF")
plt.tight_layout()
plt.show()
# 実行
print_correlation(df_train, select_columns)
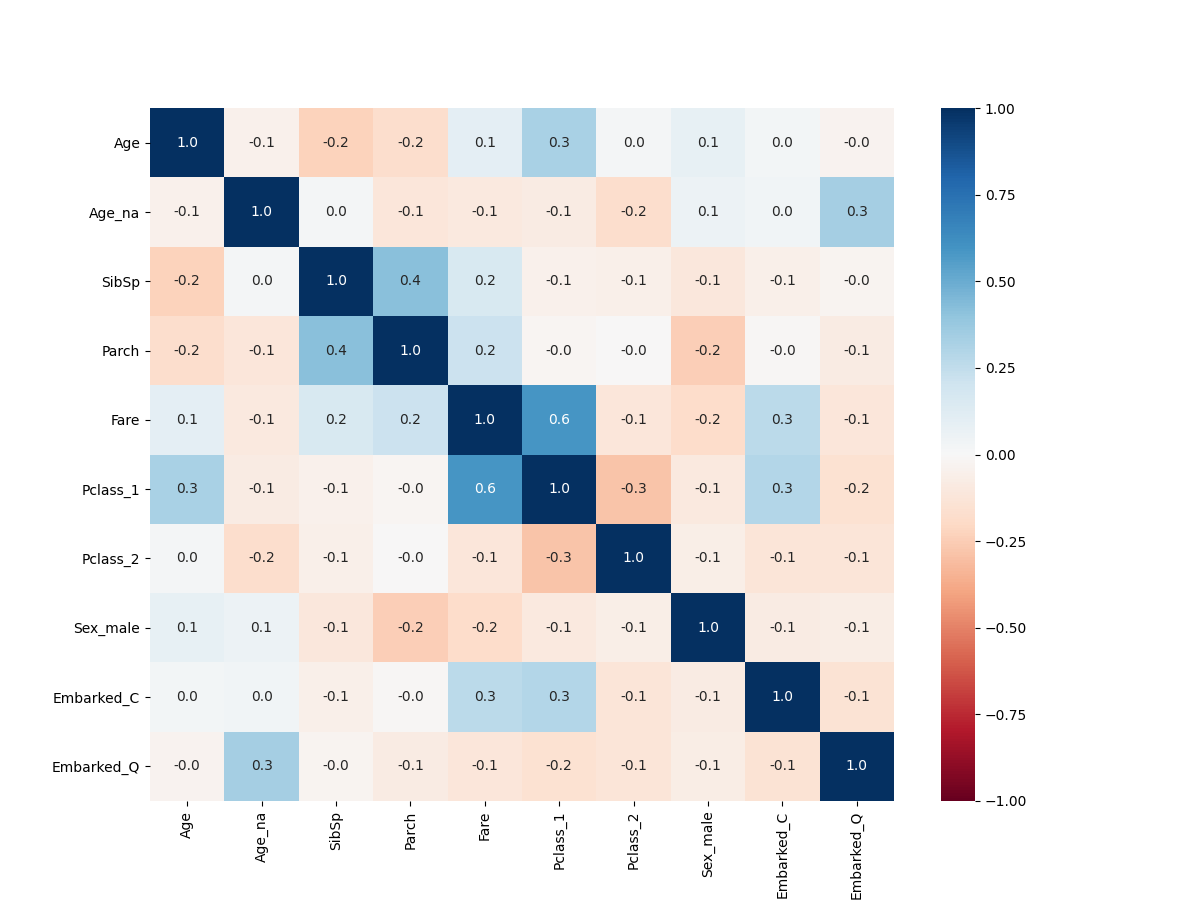
相関係数
相関係数は-1~1の値を取り、0が関係なしとなります。
表示としては、相関係数の絶対値が0.5以上のものを表示しています。
--- 相関係数1:1 (threshold: 0.5)
Fare Pclass_1: 0.59
FareとPclass_1の相関が高そうですね。
ヒートマップで表すと以下です。
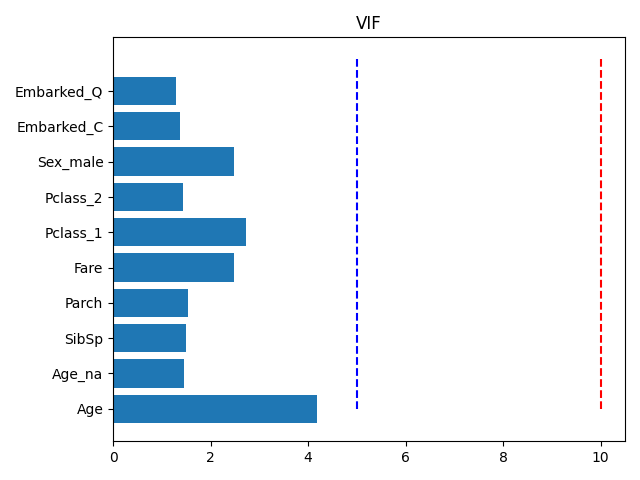
VIF
相関係数は1対1の関係を表す指標でした。
VIFは1対多で相関があるかを測る指標らしいです。
--- VIF(5以上だと怪しい)
VIF Factor features
0 4.174449 Age
1 1.453804 Age_na
2 1.504096 SibSp
3 1.543488 Parch
4 2.484896 Fare
5 2.717305 Pclass_1
6 1.428871 Pclass_2
7 2.484806 Sex_male
8 1.381078 Embarked_C
9 1.298479 Embarked_Q
5と10の地点に線を入れています。
Ageがかなり高そうですね、Pclass_1やFareも少し高そうです。
あとがき
一旦手法をまとめたかったのでまとめてみました。
次回は実際に前処理をしてスコアを上げていきたいと思います。