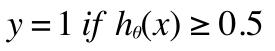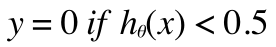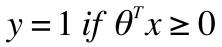7日目
Coursera でStanford が提供しているMachine Learning のWEEK 5 にながらく苦戦していたのですが、復習に復習をかさね、講座のビデオも何度も見直し、ようやく完璧に理解しました。そのおかげで、WEEK 5 の修了テストもようやく合格し、週明けからはWEEK 6 に入れそうです。
WEEK 11 まであるのでこれで折り返し。
スケジュールが少し押してしまっているので、クリスマスの3連休を使って少しずつ挽回を図ります。
過去記事一覧
- 1日目 とっかかり編
- 2日目 オンライン講座
- 3日目 Octave チュートリアル
- 4日目 機械学習の第一歩、線形回帰から
- 5日目 線形回帰をOctave で実装する
- 6日目 Octave によるVectorial implementation
- 7日目 ロジスティック回帰 (分類問題) その1
- 8日目 ロジスティック回帰 (分類問題) その2
- 9日目 オーバーフィッティング
- 10日目 正規化
- [11日目 ニューラルネットワーク #1] (http://qiita.com/junichiro/items/7794cedf834a4f6ef52c)
- [12日目 ニューラルネットワーク #2] (http://qiita.com/junichiro/items/b522ea41c02f90d23aa5)
- 13日目 機械学習に必要な最急降下法の実装に必要な知識まとめ
- 14日目 機械学習で精度が出ない時にやることまとめ
- 最終日 機械学習をゼロから1ヵ月間勉強し続けた結果
ロジスティック回帰
さて、実際の講座の進捗とこちらの日々のレポートは乖離したままですが、今日はロジスティック回帰(講座でいうところのだいたいWEEK 3 くらい)を説明したいと思います。
二値分類
腫瘍の大きさと、それが良性か悪性かどうか(二値)のトレーニングデータがあるとします。大きさをx軸に、それが悪性かどうかをy軸にプロットして、次のようなグラフが得られたとします。
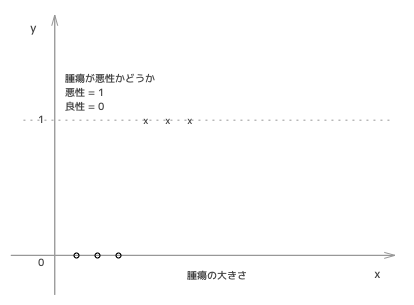
まずこれにいままでのように線形回帰を適用させてみましょう。そうすると、次のようなh(x) が引けるかと思います。
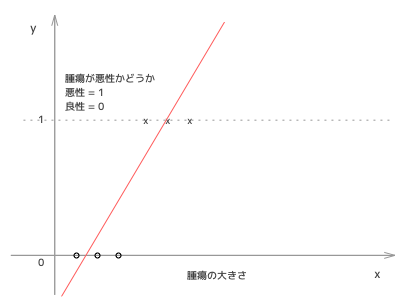
これで、もし、h(x) が0.5以上なら悪性、h(x) が0.5 未満なら良性と予測してみましょう。一見これでもうまくいきそうに見えますが、トレーニングデータに大きな腫瘍のデータが追加されたとします。すると...
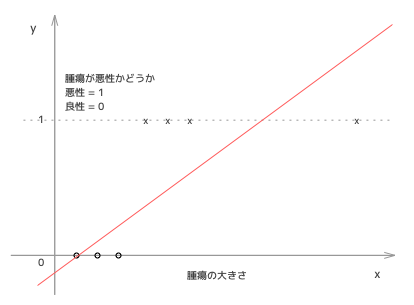
そうすると、h(x) はこのような直線になってしまい、本来悪性と予測すべきサイズでも良性と判断されかねないものとなってしまいます。そのため、こういった分類は線形回帰ではうまく表現できないということがわかるかと思います。
シグモイド関数
また、線形回帰ではh(x) が1より大きい値もとれてしまいますし、0より小さい値もとれてしまいます。しかし、二値分類におけるh(x) は0以上1以下の値域におさめたいです。そのため、シグモイド関数というものを導入します。
線形回帰におけるh(x) は  でしたが
でしたが
ロジスティック回帰ではこれにシグモイド関数(g)を適用し
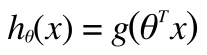
と表現されます。
ここでシグモイド関数は以下で定義された関数です。
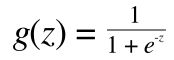
グラフの形状は次のようになります。

(y をg(z) x をz と読み替えてください)
h(x) はシグモイド関数なので、上記をシグモイド関数で考えると、
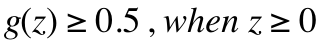
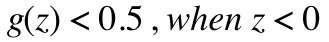
z が0以上か0未満かで境界がわかれるのがわかります。
具体例
具体例をひとつあげておきます。

このような分布のデータがあったとすると、
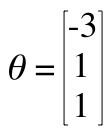
このθ を
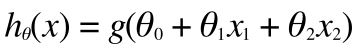
この定義に代入して、さきほどの境界を決定する式にあてはめて考えると
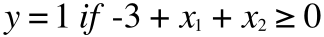
このようになり、結局
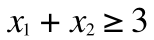
という、図の直線となります。
θの選び方
ロジスティック回帰でも線形回帰と同じようにコストを考えてみましょう。つまり、仮説関数h(x) とトレーニングデータの値y の差がコストとなります。
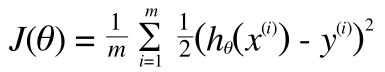
しかし、線形回帰ではこのコスト関数が凸関数(局所最小 = グローバル最小)ということが知られていましたが、ロジスティック回帰では凸関数になりません。これはh(x) がシグモイド関数であるためですが、理由などは解析的に難しい話になるのはここでは割愛し、ともかく、コスト関数をこのまま使うと、最急降下法のような局所最小を求める手順では、最小値を導くことができなくなってしまいます。
ここで、コスト関数のうち、実際のコストの部分(∑の中身)を下記のように定義しなおします。
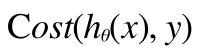
線形回帰の場合は
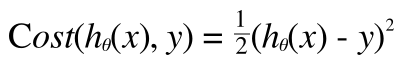
ということです。次回は、ロジスティック回帰用にこのCost(h(x), y) を定義しなおし、そのコスト関数を最小にするθを求めることで、機械学習による分類を完成させます。
講座リスケ
ちなみにオンライン講座のほうはWEEK 5 で苦戦してしまったので下記のようにリスケしています。
- 12/24(土) WEEK 6 前半 (5h46m)
- 12/25(日) WEEK 6 後半 (5h46m)
- 12/26(月) WEEK 7 (4h57m), WEEK 8 前半 (5h26m)
- 12/27(火) WEEK 8 後半 (6h9m), WEEK 9 前半 (6h9m)
- 12/28(水) WEEK 9 後半 (6h9m) WEEK 10
- 12/29(木) WEEK 11 (2h39m), WEEK 6 〜 WEEK 11 のReview とやり残し
クリスマス三連休含め、年内フル稼働でございます。