9日目
Coursera でStanford が提供しているMachine Learning ですが、今日も順調にWEEK 8 を終えました。
教師なし学習は少し後回しでいいかななんて思っていましたが、PCA による次元削減など、教師あり学習にも適用できるアルゴリズムがでてきて大変参考になりました。これもいつか紹介したいと思います。
過去記事一覧
- 1日目 とっかかり編
- 2日目 オンライン講座
- 3日目 Octave チュートリアル
- 4日目 機械学習の第一歩、線形回帰から
- 5日目 線形回帰をOctave で実装する
- 6日目 Octave によるVectorial implementation
- 7日目 ロジスティック回帰 (分類問題) その1
- 8日目 ロジスティック回帰 (分類問題) その2
- 9日目 オーバーフィッティング
- 10日目 正規化
- 11日目 ニューラルネットワーク #1
- 12日目 ニューラルネットワーク #2
- 13日目 機械学習に必要な最急降下法の実装に必要な知識まとめ
- 14日目 機械学習で精度が出ない時にやることまとめ
- 最終日 機械学習をゼロから1ヵ月間勉強し続けた結果
正規化
今日はオーバフィッティングのお話をします。相変わらず英語で講座を受けているため、日本語訳の用語がわからなかったのですが、オーバーフィッティングは日本語でいうところの「過学習」に該当するようです。過学習という言葉は以前にも少し聞いたことがあり、その時は「機械学習がなにやら学び過ぎておかしなことになっているんだな」というふうな感覚的理解を得ましたが、よく見てみると「過学習」よりはオーバーフィッティングのほうがしっくりくる現象だと感じました。
例
いきなりオーバーフィッティングの例から行きましょう。例を見るのが早いです。
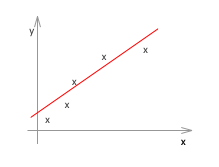
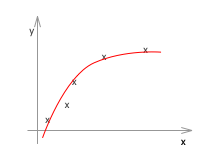
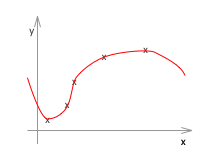
線形回帰の場合の例です。左から順にアンダーフィッティング、ちょうどよい、オーバーフィッティングです。
次にロジスティック回帰の例です。
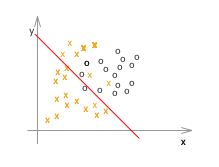
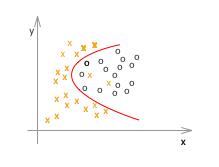
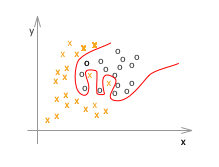
ここで、x や o はすべてトレーニングデータです。
アンダーフィッティング(左)の例は、仮説(h(x))がシンプル過ぎて、適切なθを選んだところで、トレーニングデータでさえもうまくフィットしません。一方、オーバーフィッティング(右)の例は、トレーニングデータにフィットすることに拘り過ぎて、確かに最適にフィットしている例よりもトレーニングデータに関しては完璧(誤差、エラー、コストと呼ばれるものがほぼゼロ)なのですが、未知のデータの推定や分類には適していなさそうなのが見て取れます。
これがオーバー(もしくはアンダー)フィッティングの問題です。
原因と対策
ここからはオーバーフィッティングの原因と対策を見ていきます。アンダーフィッティングについては、だいたいその逆なので省略します。
オーバーフィッティングの例はグラフや境界線が複雑な形をしているので、とても高次の関数であることが想像されます。実際、特徴量(n) が大きいときや、高次の特徴があるときにこのような問題が起きます。
また、トレーニングデータ数(サンプル数)が少ない場合にもおきてしまいます。n に対して十分に mが大きければ、それら m 個の点をすべて通るような線はn 次では表現できませんから、必然的にオーバーフィッティングしなくなることはわかるかと思います。
なので、対策としてはその逆を行うことになります。主な対策は次の2つです。
特徴(n)を減らす。
人間が見ても意味のない特徴などを減らします。例えば、家の価格の予測をするときの特徴量として、「家の広さ(平方メートル)」という特徴と「家の広さ(平方フィート)」という特徴があったとします。これは極端な例ですが、この2つには強い相関もありますから、両方を特徴として採用する意味はあまりなさそうです。こういったものは特徴から外していきます。
影響力の高い特徴の影響を減らす、正規化を施す
影響力の高い項にペナルティを課すことで、その影響の度合いを小さくする手法があります。これを正規化といいます。
正規化は次回説明します。
オーバー(アンダー)フィッティング問題まとめ
| オーバーフィッティング | アンダーフィッティング | |
|---|---|---|
| 事象 | トレーニングデータにフィットし過ぎ | トレーニングデータにすらフィットしない |
| 検定で誤差が大きい | 検定で誤差が大きい | |
| High Varians | High bias | |
| 原因 | トレーニングデータ数 m が小さい | トレーニングデータ数 m が大きい |
| 特徴量(種類) n が多い | 特徴量(種類) n が少ない | |
| 対策 | 正規化パラメタλを大きくする | 正規化パラメタλを小さくする |
| SVMの場合パラメタCを小さくする | SVMの場合パラメタCを大きくする | |
| 特徴を減らす(手動) | 特徴を増やす / 高次元の特徴を導入する |