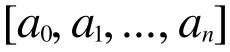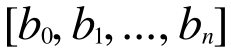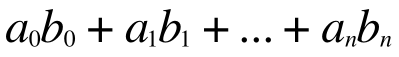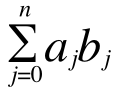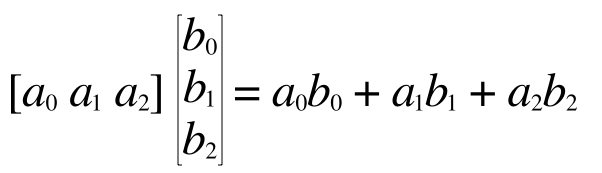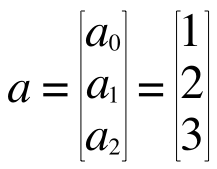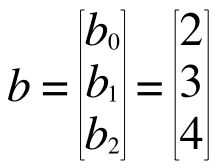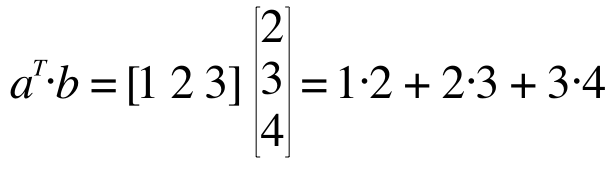More than 5 years have passed since last update.

機械学習を1ヵ月で実践レベルにする #6 (Octave 実践編)

Last updated at 2018-02-20Posted at 2016-12-21

6日目

理論を理解しても、それをOctave で実装するときにつまづくことが結構ありました。特に実数(スカラー)での定義をベクトルや行列に拡張するときに、式では理解できても、Octave で表現するときにつまづくことが多かったです。

Vectorial implementation という考え方があると少し理解しやすくなると思いましたので、ここで1日使って、このVectorial implementation を説明したいと思います。

例によって、英語しかみていないので「Vectorial implementation」日本語の該当する用語がわかりません。Google によると「ベクトル化実装」らしいです。どうもピンと来ませんが、Octave で数値計算するときに大事な考えかたなので、さっとまとめておきます。

このように要素数が同じ配列が2つあったとします。そこでいま

これを計算したいと思います。∑ を使って書くとこうなります。


a = [1, 2, 3]
b = [2, 3, 4]
ans = 0
for i, v in enumerate(a):
    ans = ans + a[i] * b[i]
print(ans)

a = [1;2;3]
b = [2;3;4]
ans = 0
for j = 1:length(a)
    ans = ans + a(j) * b(j);
end
display(ans)

∑ の計算はfor ループで書くのは直感的かと思います。

しかし、

この形は行列の積で表すこともできます。

Octave は行列の計算に長けていますから、さきほどのコードにあるa やb は行列としても扱えます。Octave の場合、配列はベクトルで、要素nのベクトルというのは n x 1 の行列に過ぎませんから、a, b はそれぞれこうなっています。

両方 3 x 1 では行列の積が作れませんので、片方を転置(T)して

このようにも表現できることがわかります。これをOctave のコードに落とすと

a = [1;2;3]
b = [2;3;4]
ans = a' * b
display(ans)

実際に計算している部分はa を転置してb に掛けるだけ。

a` * b

これでできます。これがベクトル化実装です。
コード自体がすっきりかけるだけでなく、Octave の内部で効率の良い行列計算がなされますから、実行効率もよくなります。機械学習では∑ の計算は結構でてきますので、効率の良いベクトル化実装がすぐに思い浮かぶようになるといいですね。