More than 3 years have passed since last update.

機械学習に必要な最急降下法の実装に必要な知識まとめ

Last updated at 2020-01-31Posted at 2017-01-05

機械学習を1ヵ月で実践レベルにする 13日目

この記事は「機械学習を機械学習を1ヵ月で実践レベルにする」シリーズの13日目の記事です。

初日の記事はこちら
機械学習を1ヵ月で実践レベルにする #1 (とっかかり編)

その他の記事は、本記事の末尾にインデックスをつけています。
それでは本題へ。

最急降下法

最急降下法 - Wikipedia

関数（ポテンシャル面）の傾き（一階微分）のみから、関数の最小値を探索する連続最適化問題の勾配法のアルゴリズムの一つ。

機械学習というものが何をするかざっくり説明すると、大抵は目的関数(コスト関数)を定義して、その目的関数が最小になるパラメータを決定するという流れで問題を解決します。その、目的関数を最小化するときにこの最急降下法が活躍します。英語では、Gradient descent といいます。

まず絵で考える

例えば、$ f(x) = (x-3)^2 $ という関数があったとします。この $ f(x) $ を最小化する $ x $ はなにかというと、

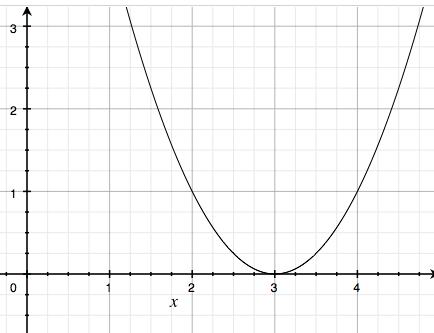
このグラフの最小値を求める問題ということになりますから、その最小値は $ 0 $ で、そのとき　$ x = 3 $ です。これは視覚的にはグラフの凸の底にあたります。

同様に $ f(x,y) = \frac{1}{5} (\frac{2}{3}x-3)^2 + \frac{1}{10}(y-1)^2 $ という関数を最小化するというのは、次の図でいう、ボウル型の底の点の値と、そのときの $ x, y $ がいくつかを求めるということになります。

いまの $ f(x,y) = \frac{1}{5} (\frac{2}{3}x-3)^2 + \frac{1}{10}(y-1)^2 $ というのは、もう少し機械学習っぽく表現すると $ x $, $y$ をそれぞれ $ x_1 $, $x_2$ と表現して次のように書き直せます。
$$ f(x_1,x_2) = \frac{1}{5} (\frac{2}{3}x_1-3)^2 + \frac{1}{10}(x_2-1)^2 $$
さらに、 $ (x_1,x_2) $ をベクトル $\mathbf{ \theta }$ と表現し、$ f(x_1,x_2) $ を $ J(\mathbf{ \theta }) $ と書くとだいぶ機械学習の目的関数っぽくなります。

$$ J(\mathbf{ \theta }) = \frac{1}{5} (\frac{2}{3}\theta_1-3)^2 + \frac{1}{10}(\theta_2-1)^2 $$

このベクトル $ \theta $ の次元数が特徴の種類の数になりますので、実際には上記のような視覚的に表現できる範囲(2次元まで)を超えてしまいますが、いまは最急降下法の説明をしたいので、上記のボウル型の図で説明します。

最急降下法による最小値発見のステップ

ランダムなスタート地点 $ \mathbf{ \theta } = ( \theta_0, \theta_1 ) $ を設定する
斜面を下る方向に少し点を進めて、$ ( \theta_0, \theta_1 ) $ をその値に更新する
2 を繰り返して、底に到達する。 -> 最小値及び、その時の $ \mathbf{ \theta } $ が決まる

先程の図でいうと、例えば $ (x, y) = (10, 8) $ みたいなところからスタートします。これはボウル型の結構上のほうの点で、そのときの $ f(x,y) = 7.58 $ くらいです。ここから斜面方向に少し動かして、$ (x, y) = (8, 6) $ あたりの位置にしますと、今度は $ f(x,y) = 3.58 $ くらいになります。だいぶ底に近づいてきていますね。これをさらに繰り返していきますと最終的には、 $ (x,y) = (4.5, 1) $ のときに $f(x,y) = 0$ とうい最小値に到達します。

斜面方向とは

今の説明における、斜面方向 というのが、このアルゴリズムの名前にもなっている最急降下 という意味になります。具体的にどういうことかというと、先程はなんとなく斜面方向といういことで、図でもあきらかでしたから、適当に $ (x, y) $ を動かしていましたが、これを正確にもっとも急斜面の方向に動かすのが最急降下法のポイントです。

そしてこの斜面方向(勾配)を求めるのが偏微分です。いまの例で言うと、 $ x $ で偏微分すれば $ x $ 方向の斜面が、 $ y $ で偏微分すれば $ y $ 方向の斜面がわかりますので、それぞれを計算することで斜面方向というものがわかります。つまり、先程の2番目のステップ「斜面を下る方向に少し点を進めて、$ ( x, y ) $ をその値に更新する」を数式で表現すると次のようになります。

x := x - \frac{\partial}{\partial x}J(x, y) \\
y := y - \frac{\partial}{\partial y}J(x, y) \\

:= はその値で更新する(代入する)という意味で使っています。
これを機械学習風の変数たちで書き直すと

\theta_1 := \theta_1 - \frac{\partial}{\partial \theta_1}J(\theta_1, \theta_2) \\
\theta_2 := \theta_2 - \frac{\partial}{\partial \theta_2}J(\theta_1, \theta_2) \\

こうなります。この偏微分の項が斜面方向を表しているというわけです。ただし、この偏微分項はあくまでも方向しか表していませんので、このままだとその大きさを表現できていません。小さく下り降りるのか、大きく下り降りるのかを表現するために、係数(機械学習では学習率と呼ばれる) $ \alpha $ を導入して、

\theta_1 := \theta_1 - \alpha\frac{\partial}{\partial \theta_1}J(\theta_1, \theta_2) \\
\theta_2 := \theta_2 - \alpha\frac{\partial}{\partial \theta_2}J(\theta_1, \theta_2) \\

このような形になります。$ \alpha $ が大きいと、一歩一歩が大きく斜面を下るイメージです。あまり大きくすると、底を行き過ぎて、少し登ってしまうので、あまり大きくはできません。かといって、小さすぎると今度は何歩も何歩も歩かないと底にたどりつかない(計算回数 = イテレーションが多い)といういことになってしまうので、適切な値が必要になります。

自分で最適な$ \alpha $を見つける場合には、いくつかの$ \alpha $を試して、値が収束するかどうかを見ながら調整することになりますが、最急降下法を解くためのライブラリなどはこの$ \alpha $の最適化もしてくれることが多いので、実際にはあまり気にする必要はありません。ただ、$ \alpha $ がなんなのか、どういう意味があるかは、最急降下法を理解する上で知っておいて損はないと思います。

まとめ

つまり、最急降下法に必要なものは次の2点だけです。

最小値を求めたい目的の関数、目的関数(コスト関数)
その全成分の偏微分項(=勾配)

そして、ほとんどの場合、実際に最小値を求めるのはライブラリに任せることになりますので(そのほうが効率が良いため)、ライブラリにはこれらの値を渡します。

実装例(擬似コードです)

J = 目的関数
grad = 目的関数の偏微分項
% fmincg は最急降下法を解くライブラリ
[theta, cost] = fmincg([J_theta, grad], initial_theta)

このように、目的関数と勾配項、それから初期値を与えると、その目的関数を最小にする、theta とそのときの目的関数の値を返してくれます。

拡張(unrolling)

ただし、上記の例でいう、theta やinitial_theta はベクトルであり、行列ではありません。行列というのは (m x n) で表現されるもので、ベクトルというのは(n x 1)で表現されるものです。線形回帰やロジスティック回帰では、特徴量はベクトルですから、その重み付けであるtheta も必然的にベクトルになります。ですからこのままで問題ないのですが、ニューラルネットワークでは、その重み付けも行列になりますから、そのままではこれらの最小化ライブラリを利用できません。そこで、行列とベクトルを相互に変換する必要があります。

unrolling

行列をベクトルに変換する

\begin{bmatrix}
a & c & e\\
b & d & f
\end{bmatrix}
=>
\begin{bmatrix}
a \\
b \\
c \\
d \\
e \\
f
\end{bmatrix}

reshape

unrolling されたベクトルを行列に戻す

\begin{bmatrix}
a \\
b \\
c \\
d \\
e \\
f
\end{bmatrix}
=>
\begin{bmatrix}
a & c & e\\
b & d & f
\end{bmatrix}

octave 実装

コードで書くとこのようになります。

A = [1 3 5; 2 4 6];
% unrolling
A = A(:)
ans =

   1
   2
   3
   4
   5
   6

% reshape
A = reshape(A, 2, 3)
>> reshape(A, 2, 3)
ans =

   1   2   3
   4   5   6

参考

ここで説明したものは、以下の記事中で使っています。主に5日目、１２日目あたりで。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up