More than 5 years have passed since last update.

機械学習を1ヵ月で実践レベルにする #11 (ニューラルネットワーク #1)

Last updated at 2017-01-10Posted at 2016-12-31

11日目

Qiita での進捗報告が2日ほど遅れてしまいましたが、粛々と進めていた Coursera でStanford が提供しているMachine Learning をとうとう修了しました。とても良い講座だったので、寄付およびモチベーション継続の目的で修了証を頂くようにしていました。

12/14にはじめて、約2週間かけて12/30 にコースを修了しました。
→ 修了証
会社から頂いている自由研究の前半の目的は達成できたと思います。

過去記事一覧

ニューラルネットワーク

1日あたりの講義の内容が厚すぎるので、こちらでは同じペースで紹介していくことはできず、かなり遅れての内容となっておりますが、今日からはニューラルネットワークの話をしたいと思います。僕にとっては、ここが最難関でした。ニューラルネットワークは、11週ある講座のうち、WEEK 4 とWEEK 5の内容に該当します。

概要

ロジスティック回帰では、線形の分類はうまくできましたが、非線形の分類にはあまりむいていませんでした。ニューラルネットワークは非線形の分類に向いており、また、二値分類ではない複数のクラスタへの分類もone-vs-all のような複雑な手順をふまず一発で行えるというメリットがあります。

例えばこのような図があるとします。

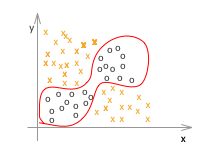
これをロジスティック回帰でモデルを作ろうとすると、おそらくたくさんの特徴(n)がでてきて、その境界のグラフはかなり高次になることが予想されます。これは計算量的にも大きな問題となります。

そういった問題にも対応できるのがニューラルネットワークです。ニューラルネットワークという言葉は「脳のニューロンの動きと同じように学習する」というところからきています。

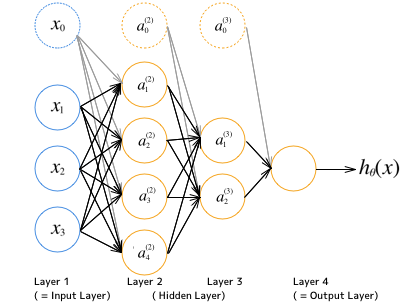
ニューラルネットワークの模式図

いきなり図を書きましたが、入力 $ X $ (特徴ベクトル)があり、そこになんらかの作用を及ぼして、最終的に仮説を出力するといういままでの構図と変わりはありません。ニューラルネットワークの場合、それが複数回の処理に及んでおり、それぞれの処理ステップをレイヤーと呼んでいます。

上記の例は、Input レイヤーとOutput レイヤーを含めて４つのレイヤーを持ちます。また、各レイヤーの要素はユニットと呼ばれています。レイヤー１のユニットはその特徴に対応しています。レイヤー２には4つのユニットがあり、レイヤー3には2つのユニットがあるという形です。

また、それぞれのレイヤーはバイアス項を持ちます。$ \theta_0 $ に対応する項として用意していた、値が1に固定されている要素です。上記例で言う、$ x_0, a_0^{(2)}, a_0^{(3)} $ がそれに当たります。

計算の流れとしては、

Layer 1(入力レイヤー)のユニットにバイアス項を追加してから Layer 2 のユニットを計算
Layer 2 のユニットにバイアス項を追加してからLayer 3 のユニットを計算
Layer 3 のユニットにバイアス項を追加してからLayer 4(出力レイヤー)を計算

となります。レイヤーから次のレイヤーに変換するための $ \theta $ が、各レイヤー間にそれぞれ必要になります。

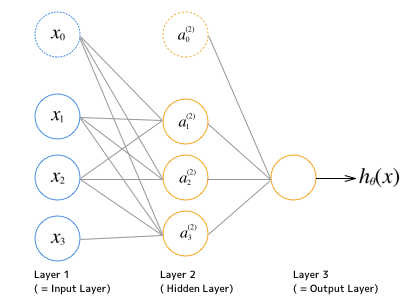
ビデオの後半で教授入っていましたが、実際には隠しレイヤーがひとつあれば十分に複雑な非線形の分類に対応できることが多いということでした。その場合、レイヤーは3つということになります。

ロジスティック回帰もこれのシンプルなものと考えることができます。その場合レイヤーは２つとなります。input レイヤーとoutput レイヤーだけで、隠しレイヤーはありません。

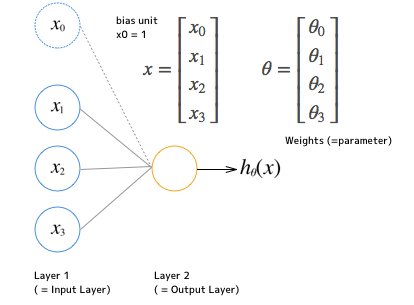
これの $ x $ と $ \theta $ を下記のようにしたロジスティック回帰です。

x = 
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 
\end{bmatrix}
 ,
\theta = 
\begin{bmatrix}
\theta_0 \\
\theta_1 \\
\theta_2 \\
\theta_3 
\end{bmatrix}

実際には $ x_0 $ のバイアス項を入れた下記の形となり、

x = 
\begin{bmatrix}
x_0 \\
x_1 \\
x_2 \\
x_3 
\end{bmatrix}
 ,
\theta = 
\begin{bmatrix}
\theta_0 \\
\theta_1 \\
\theta_2 \\
\theta_3 
\end{bmatrix}
,
x_0 = 1

$ h_\theta(x) $ は次のように表現されます。

h_\theta(x) = g(\theta^Tx)

ここで $ g(z) $ はactivation 関数と呼ばれるものですが、sigmoid 関数と全く同じものなので、これはすなわち、ロジスティック回帰の仮説関数となります。(sigmoid 関数はニューラルネットワークではactivation 関数と呼びます)

g(z) = \frac{1}{1+e^{-z}}

ニューラルネットワークはこの入力と出力の間に隠しレイヤーを持ちます。入力を受け取って、それに $ \theta_1 $を適用させ、中間出力にあたるLayer 2 のVector を返し、さらにそれに$ \theta_2 $を適用させて、最終出力を得ます。おおざっぱにいうと、ロジスティック回帰をn回実行するイメージです(この例では2回)

次の様な図のニューラルネットワークがあるとします。

ここで
$ a_i^{(j)} = $ 「j番目のレイヤー(Layer j)のi番目のユニット」で、
$ \Theta^{(j)} $ = 「j番目からj+1番目のレイヤーに対する重み付け行列」です。
各レイヤーのユニット数を $ s_j $ とすると、$ \Theta^{(j)} $の次元は
$ 「s_{j+1} \times s_j + 1 $」となります。

$$ \Theta^{(j)} \in \mathbf{R}^{s_{j+1} \times s_j+1} $$

そしてこれを式で表すと以下のようになります。

a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \\
a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \\
a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \\
h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)})

そしてこの $ h_\Theta(x) $ を最小化する $ \Theta $ たちを決定することでニューラルネットワークを解いていきます。それは次回やります。

ニューラルネットワークの分類例

さて、冒頭であげたこのような分布のデータセットがあるとします。人間の目としてはシンプルかもしれませんが、式で表すとなると線形ではないため、ロジスティック回帰では複雑なものになります。こういったものをニューラルネットワークでは簡単に表現することができます。

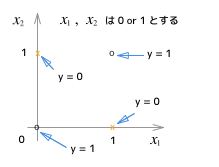
簡単に考えるために4つの点で考えて見ます。

$ x_1 $ と $ x_2 $ は 0 または1 しか値に取らないとします。

$ y = 1 $ if $ x_1 = 0 $ and $ x_2 = 0 $
$ y = 0 $ if $ x_1 = 0 $ and $ x_2 = 1 $
$ y = 0 $ if $ x_1 = 1 $ and $ x_2 = 0 $
$ y = 1 $ if $ x_1 = 1 $ and $ x_2 = 1 $

つまりこういうことです。これをロジスティック回帰の $ \theta $ で表現するのは大変だと思いますが、ニューラルネットワークであれば、隠しレイヤーをひとつ用意するだけで、下記のように簡単に表現できます。

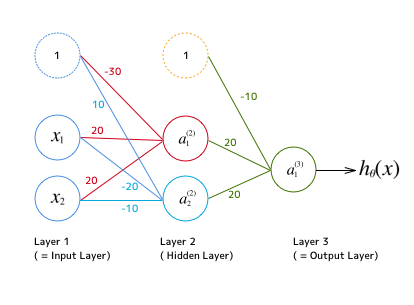
これで上記のXOR を表現できています。確かめるためにはわかっている値を代入して実際に計算してみればOKです。

\Theta^{(1)} = 
\begin{bmatrix}
-30 & 10\\
20 & -20 \\
20 & -10
\end{bmatrix}
,
\Theta^{(2)} = 
\begin{bmatrix}
-10 \\
20 \\
20
\end{bmatrix}

これを式で表すと

a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2) \\
a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2) \\
h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)})

わかっているところの値を代入して

a_1^{(2)} = g(-30 + 20x_1 + 20x_2) \\
a_2^{(2)} = g(10 - 20x_1 - 10x_2) \\
h_\Theta(x) = a_1^{(3)} = g(-10 + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)})

sigmoid 関数 $ g(z) $ の性質として $ z = 0 $ のときに $ 0.5 $ となり、$ z >= 4.6 $ でほぼ $ 1 $ となり、 $ z <= -4.6 $ でほぼ $ 0 $ となることから、 $ x_1 $ や$ x_2 $ に 0 や 1 を代入して、y が想定した値になることを確認できます。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up