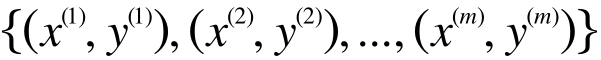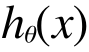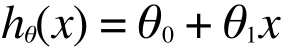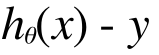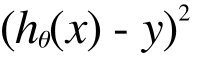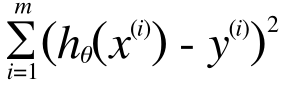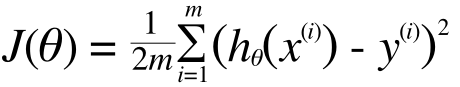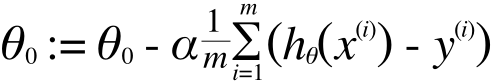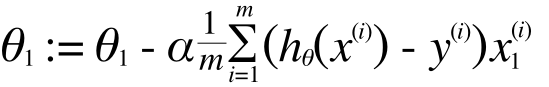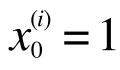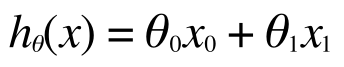5日目です
今日でCoursera でStanford が提供しているMachine Learning のWEEK 5 までが終わる予定だったのですが、WEEK 5 が手強かったです。時間的には結構余裕があって、しっかり講座を聞いたのですが、最後のテスト(講義内容をOctave で実装)が、難易度的にできませんでした。
これは悔しいですね。Forum で聞く英語力もないので、大学ノート片手に、もう一度講座のWEEK 1 から振り返り、理解している内容をアナログなノートにまとめました。明日もう一度挑戦します。
過去記事一覧
- 1日目 とっかかり編
- 2日目 オンライン講座
- 3日目 Octave チュートリアル
- 4日目 機械学習の第一歩、線形回帰から
- 5日目 線形回帰をOctave で実装する
- 6日目 Octave によるVectorial implementation
- 7日目 ロジスティック回帰 (分類問題) その1
- 8日目 ロジスティック回帰 (分類問題) その2
- 9日目 オーバーフィッティング
- 10日目 正規化
- 11日目 ニューラルネットワーク #1
- 12日目 ニューラルネットワーク #2
- 13日目 機械学習に必要な最急降下法の実装に必要な知識まとめ
- 14日目 機械学習で精度が出ない時にやることまとめ
- 最終日 機械学習をゼロから1ヵ月間勉強し続けた結果
線形回帰をOctave で
とはいえ、まだここに書いていない機械学習知識がいくつかたまっているので、記事は引き続き進めて行こうと思います。昨日は、線形回帰で土地の広さから家の売価を求めるところを、数学的にお話しました。あの内容を理解したうえで、それをどうプログラミングに落としていくか、Octave を利用して見ていきたいと思います。
線形回帰の復習
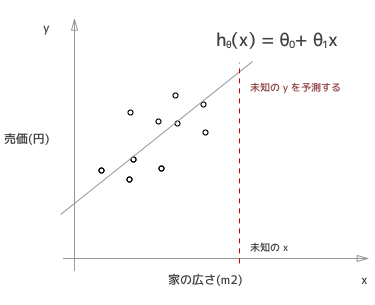
前回同様、家の広さから家の売価を予測するということをやっていきます。
このグラフの中で「o」で示されているのが、実際に売れた家の広さと売価をプロットしたものです。広さをx 軸にとり、売価をy軸にとっているので、これらの点は下記のようにあらわされます。
m はトレーニングデータの個数で、今の場合は「o」の点が10個あるので m = 10 です。変数のままだとわかりにくいというかたも多いと思いますが、この数字がかっこで上に付いているものは、あたえられたトレーニングデータなので、実際の数字です。(75, 7200万), (68, 4500万), ... , という風に、75平米で7200万で売れたとか、68平米の家が4500万円で売れたとかそういうデータの集合です。
そして、これらのデータから、未知のx つまり、新しい例えば100平米のこの家がいくらで売れるか(予測したい未知のy)を予測したいのです。
そのために、この予測の線を引きました。これを仮説関数(英語の講義なので技術用語の日本語訳がわからないw) Hypothesis function といいまして、h(x) で表します。
で、これを直線であると仮定してこのように表現します。
ここで、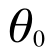
はh(x) の切片(y軸との交点)で、
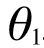はこの直線の傾きを表します。
そして、この直線が、まずはトレーニングデータにもっともフィットするようにθを決めていきます。
最急降下法 (これも日本語訳はわからん)
さて、どのようなθにするのが、もっともよくトレーニングデータたちにフィットするでしょうか。それは、このh(x) が予測する値と実際のトレーニングデータとの乖離が小さくなればよいので、すべてのトレーニングデータのx(家の広さ)に対して、h(x) で予測した場合に出る売価と、実際の売価(y) の差が小さくなればよいということになります。
つまりこれが小さく慣ればいいのです。トレーニングデータはたくさん(今の例では10個)ありますから、これらの差の合計が小さくなると嬉しいですね。差には、正の差と負の差があるので、二乗して、差の向き(高すぎるか安すぎるか)を無視して、差の大きさだけに着目できるようにします。この差をコストと呼びますね。
これをすべてのトレーニングデータに対して計算して、その総和が小さくなれば良いので、この総和を出します。
∑とかが出てくると急にわかりにくいと思ってしまうかもしれませんが、これは簡単です。i = 1 から i = m までの、コストの合計を意味します。今の場合m = 10 ですから、つまりこれで、トレーニングデータすべてのコストの合計をあらわしています。
これに今後の数値計算が楽になるように、便宜上の係数(1/2m)をかけて(θに依存しない係数であればなにを掛けても総和を小さくするθには影響がない)、次のような式を定義します。
これをコスト関数と呼びます。コスト関数はθの関数です。
コスト関数を最小にするθを探す
「最小値を求めるのは微分」と、高校生のときに習ったことを思い出してください。これはもう昔から決まっていることなので、ここでも同様です。
今回の場合、θは実際には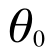と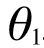ですから、それぞれに対して偏微分が必要になります。高校生の時に習った微分とは少し違うかもしれませんが、あまり気にしなくていいでしょう。
微分すれば、その点における傾きがわかりますので、その傾き方向に向かって少しずつθを変化させていき、収束したところが最小というわけです。
ここは少し難しいので結果だけ書いておきます。
:= というのはプログラミング言語でいう「=」と同じで、代入を表します。この計算を繰り返すことで、θは、J(θ) を最小化する方向に収束していきます。いま、θはθ0とθ1だけでしたからこのように2つにわけて書きましたが、
とうい定義を導入すると、
これを
と書き直すことが出来、ゼロ番目の項と1番目の項が同じように書けましたので、場合分けなしで一般化して下記のように書き直せます。
あとはこれをOctave で表現して、実行させれば最適なh(x) を作り出すことができます。ひとたびh(x) を作り出せれば、あとは未知のx に対してこれを適用していくだけで、価格の予測ができるようになるわけです。
Octave 実装
コスト関数
Octave
function J = computeCost(X, y, theta)
m = length(y);
J = 1/2/m * sum((X * theta - y).^2);
end
最急降下法
Repeat {
}
Octave
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
m = length(y);
for iter = 1:num_iters
theta = theta - alpha / m * X' * (X * theta -y);
end
end
おわりに
数式を理解しても、それをOctave で実装するときに、行列やベクトルがどういう形をして、それらの積の演算などがどういう結果になるかをイメージしながら、転置させたり、掛け算の向きを変えたりするのがとても苦労します。そこに対しての説明を少し省いてありますので、そのあたりは上記の結果を参考にしてみてください。とりあえず (m x n 行列) x (n x o 行列) = (m x o 行列)ということを理解していれば、まず、できない掛け算をしないようになりますし、それから、結果的にどういう次元の行列が欲しいかというところから、何を転置させればいいかなどの想像がつくようになります。
いつか機会があれば実例で示そうと思いまます。例えば、最後の最急降下法のところなんかは、数式には∑があるのに、Octave 実装ではsum もでてきません。これは行列の積を使えばsum が不要になることもあるからです。
詳しくはこちらに追記しました。
Octave によるVectorial implementation
(機械学習を1ヵ月で実践レベルにする #6 (Octave 実践編))