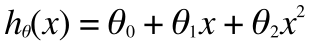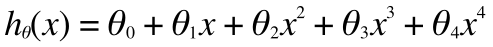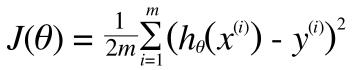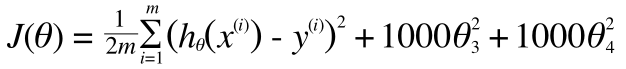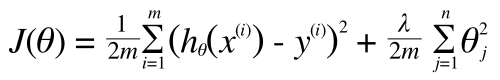More than 5 years have passed since last update.

機械学習を1ヵ月で実践レベルにする #10 (正則化)

Last updated at 2018-03-07Posted at 2016-12-29

10日目

Coursera でStanford が提供しているMachine Learning ですが、今日も順調にWEEK 9 を終えました。

過去記事一覧

正則化

昨日、オーバーフィッティングの問題の例を見ましたが、今日はオーバーフィッティングを是正する、正則化についての話です。

正則化についての僕の考え

僕は個人的に、この正則化ってやつは機械学習の肝のひとつだと思っています。例えば最急降下法は、式は難しくても内容としては「予測と実測の差を小さくする方法」というように直感的にわかりやすいです。しかし正則化はこれらに比べると直感的な理解が得にくいです。それにも関わらず、また、一見重要性も理解しにくい割に、実際にはとても重要であるからです。

あとのほうの講座でも正則化にはたびたび触れることになりますので、ここでしっかり理解しておかないと後がきつくなります。

考え方

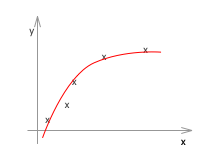
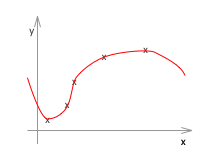
もう一度、ジャストフィットした例と、オーバーフィッティングした例を見てみます。

右のグラフを左のようなグラフの形状に近づけるのが目的で、それこそが正則化です。
いま、左のグラフは、その形状から類推すると、おそらく2次くらいの関数なので次のような式で表すことができるかと思います。

次に右のグラフですが、こちらは左に比べて複雑なのでおそらく高次の項があり、それは例えば4次くらいの関数であり、次のような式で表すことができます。

この2つの式を比べるとわかると思いますが、右(下)のグラフの式の高次の項の影響が少なくなれば、左(上)のグラフ(の式)に近づきます。これを踏まえた上で、もう一度、コスト関数を最小化することに立ち返ってみます。

技巧的ですが、ここに高次の項のペナルティを課してみます。

そうすると、最急降下法などで上記のコストを最小にするためのθを選ぼうとすると、必然的にθ3やθ4は0に近い小さい数字となります。その結果、右のグラフはより左のグラフに近づきます。いまのように掛ける数字を大きくすると、θ３やθ4は小さくなり、右のグラフに近づき、掛ける数字を小さくすると、右のオーバーフィットしたグラフになることがわかります。

これを一般化して正則化項を導入したコスト関数は以下のようになります。

追加された第2項が正則化のための項です。これで、λ を調整することで適合度を、オーバーフィッティングしないようにコントロールできるようになります。

オーバーフィットしている場合 -> λ を大きくしてグラフを滑らかにする
アンダーフィットしている場合 -> λ を小さくしてグラフをもう少し複雑にする

正則化項付きの最急降下法

コスト関数

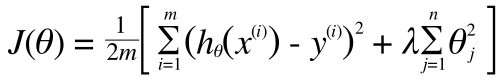
(正則化は切片項のθ0には適用しないため、ｊ = 1 からの和をとります)

最急降下法はやはり偏微分です。

Repeat {

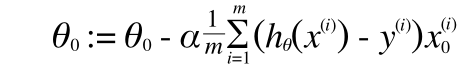
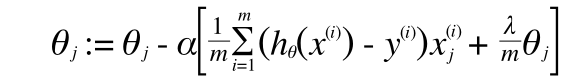
(j=1, 2, 3, ..., n)
}

正則化あり線形回帰のoctave 実装

2018/03/07 に修正しました。

コスト関数

hx = X * theta;
cost = hx - y;
theta = [0; theta(2:end, :)];
J = ((cost' * cost) + lambda * (theta' * theta)) / (2 * m);

最急降下法の偏微分項

grad = (X' * cost + lambda * theta) / m;

あとはこれを計算ライブラリに渡せばモデルを得られます。

2018/03/07 の修正ここまで。

正則化ありロジスティック回帰のoctave 実装

J = -1/m * sum(y .* log(sigmoid(X * theta)) + (1 - y) .* log(1 - sigmoid(X * theta))) + lambda / 2 /m * sum(theta(2:end,:).^2);

最急降下法の偏微分項

grad = 1/m * (X' * (sigmoid(X * theta) - y)) + lambda / m * [0 ; theta(2:size(theta), :)];;

以上。

最適なλやαを決定する話はまた機会があればします。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up