More than 5 years have passed since last update.

機械学習を1ヵ月で実践レベルにする #4 (線形回帰編)

Last updated at 2017-01-10Posted at 2016-12-19

4日目です

週末に挽回して、今日でCoursera でStanford が提供しているMachine Learning のWEEK 4 まで終わらせました。WEEK 4 というと、なんとすでにニューラルネットワークの入門にまで差し掛かっていて、教授がいうには、シリコンバレーで機械学習エンジニアとして活躍している人のほとんどよりは、あなたのほうがすでに上であろう、ということです。ほんまかいなｗ

過去記事一覧

そういえば講義の進め方など

4日目修了の図

この講義は各週にだいたい2〜3回くらい小テスト(Quiz)があって、それは80%以上の正答率を出さないと次に進めません。Retake は8時間で3回までなので、3回失敗すると、しばらく先に進めなくなります。僕のように毎日1週分をやるという高速性が必要な場合には致命的となりますから、かなり慎重になりますし、3回目のチャレンジにまでなってしまった場合には、相当復習をして背水の陣でのぞむことになります。

結果的にとても身につきます。

それから各週の最後には「Programming Assignment」という、所要時間3時間くらいのOctave のテストがあります。学んだことをOctave で実装せよという内容です。こちらは正答率100% にならないと次に進めませんが、Retake は何度でも可能です。

ちなみにQuiz もProgramming Assignment も、他かからのコピペはしないという誓約をさせられますし、それを違反してバレた場合には、本コースから追放されることになります。

特にProgramming Assignment は難しいことも多く、英語ができる方であればForum の力を借りながらやるのも良いと思います。僕はForum で英語コミュニケーションを頑張るくらいなら、Octave のマニュアルや、それまでの講義の内容を何度も復習するほうを選びましたが。でも、本当に難しいです。まだ1/3 ですが、ここまで止まらずに来れている自分を褒めたいです。

線形回帰

毎回その講義内容をレポートしようと思っていましたが、週末の挽回でだいぶ進んでしまったうえに、週末はQiita を書く元気までは残っていなかったので、復習も兼ねて、線形回帰から順に要約していきたいと思います。

家の売価予測

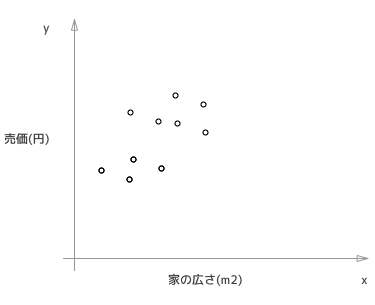
抽象的な話を理解するのは難しいので、具体例で示して行きたいと思います。ここに(家の広さ, その家の価格)というデータセットがいくつかあるとし、それをプロットしたものが次の図です。

これを予めわかっている(事実)データとして、いわゆる機械学習でいうところの「トレーニングセット」とします。こういう前提のもとで、新たに「家の広さ = x」の物件がでてきたときに、その売価を予測するのが、線形回帰の問題です。これはこういう事実(=教師データ)があるので「教師あり学習」に分類される問題です。

線形回帰

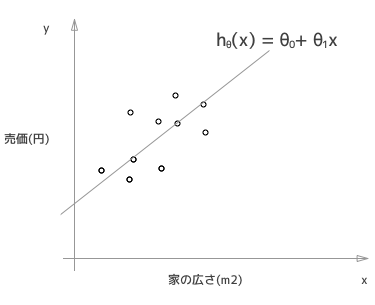
これらのトレーニングデータから、家の広さと売価には下記の様な直線(関数)の関係があるのではないかと仮説(hypothesis)を立てます。なのでその関係を表す関数をhypothesis function といい、h(x) と表します。

θを決定する

このh(x) を最適化するθというのを決定しなければなりません。どのように決めるかといいますと、h(x) と y(トレーニングデータの値 = つまり図中のo点)の距離が小さければ、それは良いθだと言えるのは直感的であると思います。

数式をきれいに書けないので、距離を小さくするということを感覚的な形で言い換えますと、つまり、「h(x) - y」の二乗が小さくするということになります。

ですから、トレーニングデータ全ての点に関して「h(x) - y」の二乗の総和が最も小さくなるように、θを決めれよいわけです。(ここでθというのはθゼロとθワンのこと)

θを求めるアルゴリズム

前述の、二乗の総和をコスト関数と呼びます。

コスト関数(θ) = 総和(h(x)-y)^2

コストが0になるようなθであれば、完全にトレーニングデータにフィットしているということになりますが、そういうケースはめったにありませんから、何らかの最小値を求めることになります。

コスト関数はh(x) の中身がθゼロとθワンに依存することを考えると、結局その2変数(二元)の二次関数になりますから、それは3次元空間のなかで、ボウル(お料理に使うボウル)のような形状になります。ここでは解析的な詳細ははぶきますが、そのボウルは極小値 = 最小値となる、局所最適解がグローバル最適解になることが保証されています。

ですから、コスト関数を最小化するθを、求めるのに最急降下法が使えます。

最急降下法

きれいな絵がないので、ここからはみなさんのイメージを膨らませて頂きたいのですが、とってもカラダが小さくなって、ボウルのどこか好きな一点に立っているところを想像してください。そこから周囲を見渡し、もっとも急斜面の方向に少し降りてください。それからまた、周囲を見渡し、もっとも急斜面の方向に少し降りてください。それを繰り返すと、ボウルのそこ、つまり最小値にたどりつけるということになります。

上記でいう、最も急斜面の方向というのが、θに対する微分(微分というのはその点における接線の傾き)ということになりますから、0ゼロについてはθゼロで偏微分し、θワンについてはθワンで偏微分して、その方向に少しずつθを変化させていきます。

ボウルの例をもう一度イメージして頂くとわかると思いますが、初期値はなんでも大丈夫です。どこからスタートしても、ある程度のステップを繰り返せば必ずそこにたどり着きますから。

追記：最急降下法の説明を別の記事で書きました。
機械学習に必要な最急降下法の実装に必要な知識まとめ

学習係数

最急降下法にはもう一つ重要な「学習係数：(α)」というパラメタがあります。先程のボウルの例でいうと、降りる時の歩幅にあたります。あまり大きな歩幅で降りようとすると、底を通りこして、逆側の斜面に足を運んでしまうことになります。こうなると悪いときにはいつまでたっても底にたどり着かなくなってしまいます(= 収束しなくなる)

一方で、あまりにも小さな歩幅では、なんどもなんども歩かなければ底にたどりつきません。これは大量の計算回数を必要としてしまうということを意味しています。αは適宜決めて、データの収束の仕方などを見て、経験的に出すのが一番手っ取り早いと言っていました。

まとめ

こうして機械学習のもっともシンプルにして、他への応用の基礎にもあたる線形回帰を理解することができました。今後はこれを多変量に発展させ(いまは家の広さという単一変数でした)、さらには予測ではなく分類(ロジスティック回帰)に発展させ、さらにそれを非線形のデータに応用できるようにと進化していきます。

またこれらをOctave で実装できるようにもなっていきます。

本当に機械学習の知識ゼロからでもここまでたどり着けます！

お詫び

数式をほとんど書いていないのでわかりにくいと思いますが、少なくとも僕はここまでは100%完璧に理解しています。質問があったらコメントでなんでも聞いてください！必要があれば手書きででも、適宜数式や説明の補足は追記するつもりです。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up