More than 5 years have passed since last update.

機械学習を1ヵ月で実践レベルにする #12 (ニューラルネットワーク #2)

Last updated at 2017-01-10Posted at 2017-01-04

12日目

あけましておめでとうございます。年をまたいでしまいましたが、今日は前回の続き、ニューラルネットワークの解決編です。

過去記事一覧

ニューラルネットワークでモデル化する

前回はニューラルネットワークとはどういうものか、それからその表現の仕方を、図とベクトルと式とで見てきました。今日はその仮説関数から導出されるコストを最小にすべく、どのように $ \Theta $ を決定するかを見ていきます。

二値分類から複数の分類への一般化

前回の例では、出力レイヤーのユニット数を1としていました。これを分類の問題に当てはめて考えると、出力が $ y = 1 $ or $ 0 $ という形になります。

複数の値への分類を考える場合は、$ y $ は分類の種類、つまり出力レイヤーのユニット数と同じ次元を持つベクトルとなります。例えば「ある記事を金融、政治、テクノロジーの3つのどれかに分類する」という問題を考えましょう。その場合、図はこのようになります。

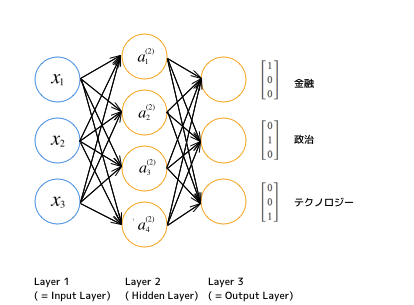
そして、二値分類のときに 0 or 1 という実数だった $ y $ の値は、K種類に分類するマルチクラス分類の場合、

 y \in \mathbf{R}^K \\
E.g.
\begin{bmatrix} 
1 \\
0 \\
0
\end{bmatrix}
,
\begin{bmatrix}
0 \\
1 \\
0
\end{bmatrix}
,
\begin{bmatrix}
0 \\
0 \\
1
\end{bmatrix}

となります。例は、3クラス分類の場合です。

コスト関数

コスト関数の考え方は基本的にはロジスティック回帰のときと同様です。

ロジスティック回帰のコスト関数(再掲)

J(\theta) = -\frac{1}{m} \Bigl[\sum_{i=1}^m y^{(i)}\log h_\theta(x^{(i)}) + (1 - y^{(i)})\log(1 - h_\theta(x^{(i)}))\Bigr] + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2

ニューラルネットワークのコスト関数

ニューラルネットワークの場合、K個の出力ユニットにわかれているので、それらの和をとったものがそのコストになります。つまり、下記のようになります。

J(\Theta) = -\frac{1}{m} \Bigl[\sum_{i=1}^m\sum_{k=1}^K y_k^{(i)}\log(h_\Theta(x^{(i)}))_k + (1 - y_k^{(i)})\log(1 - (h_\Theta(x^{(i)}))_k)\Bigr] + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_{j+1}}(\Theta_{ji}^{(l)})^2

第二項(正規化項)は、全レイヤー間の全 $ \Theta $ の全要素の二乗の総計に$ \frac{\lambda}{2m} $ を乗じたものです。それから、このコストを最小にするための$ \Theta $を決定します。方法としてはいままでと同様に、$ \Theta $ の各レイヤーの各要素における偏微分を計算して、最急降下法を適用していきます。

フォワードプロパゲーション

まず、あるひとつのトレーニングサンプル $ (x, y) $で考えてみます。 $ x $ を仮説関数に入れて、レイヤーを進める方向(フォワード)に計算していきます。

\begin{align}
a^{ (1) } &= x \\
z^{ (2) } &= \Theta^{ (1) }a^{ (1) } \\
a^{ (2) } &= g(z^{ (2) }) \quad (add \quad a_0^{(2)}) \\
z^{ (3) } &= \Theta^{ (2) }a^{ (2) } \\
a^{ (3) } &= h_\Theta(x) = g(z^{ (4) })
\end{align}

バックプロパゲーション

次に、これを遡るように(バック)計算していき、差分と偏微分を求めます。
ここでまず、レイヤー $ l $ における、ノード $ j $ の誤差を $ \delta $ とします。
$$ \delta_j^{(l)} = 「レイヤー\quad l \quadにおけるノード \quad j \quad の誤差」 $$

\begin{align}
\delta_j^{ (3) } &= a_j^{ (3) } - y_j
\end{align}

これは、各ノード $ j $ について表現したものですが、ノードをまとめてベクトルで表現しても同様ですので、 $ j $ をとります。

\begin{align}
\delta^{ (3) } &= a^{ (3) } - y
\end{align}

ここで $ a_j^{ (3) } $ は仮説関数の出力 $ (h_\Theta(x))_j $ です。この出力レイヤーの $ \delta $ からレイヤーをさかのぼって、順次手前のレイヤーの $ \delta $ を求めていきます。

バックプロパゲーションについては解析的な説明(証明)を省略しますが、以下、 $ \delta $ を遡る式です。

\begin{align}
\delta^{(2)} = (\Theta^{ (2) })^T \delta^{ (3) }.*g'(z^{ (2) })
\end{align}

隠しレイヤーがひとつしかないので、今回の例ではこれでバックプロパゲーションは終わりますが、隠しレイヤーがもっとあれば、その分さかのぼって計算することになります($ \delta^{ (1) } $ は入力における誤差という意味になり、入力時は誤差がないのでこれは存在しません)。

ちなみに、

g'(z^{(l)}) = a^{(l)}.*(1-a^{(l)})

ですので、これも証明は省略しますが、Octave で実装するときなどはお使いください。
それでは、次に、このバックプロパゲーションを m 個のトレーニングセットに拡張します。擬似コードとして書いていくのでわかりにくく見えるかもしれませんが、これが一番わかりやすいと思います。

m 個のトレーニングセット: $ \Bigl[\hspace{3pt}(x^{(1)}, y^{(1)}),\ldots,(x^{(m)}, y^{(m)})\hspace{3pt}\Bigr] $
誤差行列を初期化: $ \Delta_{ ij }^{ (l) } = 0 \quad (for \hspace{3pt} all \hspace{3pt} l, i, j). $
For $ i = 1 $ to $ m $ (つまりすべてのトレーニングセットについて)
$ \quad $ Set $ a^{(1)} = x^{(i)}$
$ \quad $ フォワードプロパゲーションを計算していく: $ a^{(l)} $ for $ l = 2, 3, \ldots, L $
$ \quad y^{(i)} $ を使って $ \delta^{(L)} = a^{(L)} - y^{(i)} $ を計算する。
$ \quad $ そこからさかのぼって $ \delta^{(L-1)}, \delta^{(L-2)},\ldots,\delta^{(2)} $ を計算する。($ \delta^{(1)} $ は不要)
$ \quad \Delta_{ij}^{(l)} := \Delta_{ij}^{(l)} + a_j^{(l)}\delta_i^{(l+1)} $
$ \quad $ ベクトル表記で書けば $ ij $ をとりのぞけますので、
$ \quad \Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T $
$ \quad $ となります。

$ D_{ij}^{(l)} := \frac{ 1 }{ m }\Delta_{ ij }^{ (l) } + \lambda \Theta_{ ij }^{ (l) } \hspace{3pt} if \hspace{3pt} j \neq 0 $
$ D_{ij}^{(l)} := \frac{ 1 }{ m }\Delta_{ ij }^{ (l) } \hspace{31pt} if \hspace{3pt} j = 0 $

こうして、勾配項が得られました。

そして、このコスト関数と勾配項から、最急降下法を使ってコストを最小化する $ \Theta $ が求められます。

Octave での実装

下記のOctave での実装では、unrolling(行列をnx1ベクトルに変換) を行って計算効率をあげています。

追記: unrolling について下記の記事で少し補足しました。
機械学習に必要な最急降下法の実装に必要な知識まとめ

function [J grad] = nnCostFunction(nn_params, input_layer_size, hidden_layer_size, num_labels, X, y, lambda)

% reshape
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), num_labels, (hidden_layer_size + 1));

m = size(X, 1);

J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));

Y = zeros(m, num_labels);
for i = 1:size(y)
  Y(i,y(i)) = 1;
end

a1 = X;
a1 = [ones(m, 1) a1];
z2 = a1 * Theta1';
a2 = sigmoid(z2);
a2 = [ones(m, 1) a2];
z3 = a2 * Theta2';
a3 = sigmoid(z3);
hx = a3;

J = -1/m * sum(sum(Y .* log(hx) + (1 - Y) .* log(1 - hx)));
J = J + lambda / 2 / m * (sum(sum(Theta1(:,2:end).^2)) + sum(sum(Theta2(:,2:end).^2)));

d3 = a3 - Y;
d2 = (d3*Theta2) .* sigmoidGradient([ones(size(z2, 1), 1) z2]);
d2 = d2(:, 2:end);

r2 = lambda / m * [zeros(size(Theta2, 1), 1) Theta2(:, 2:end)];
r1 = lambda / m * [zeros(size(Theta1, 1), 1) Theta1(:, 2:end)];

Theta2_grad = 1/m * (d3' * a2) + r2;
Theta1_grad = 1/m * (d2' * a1) + r1;

% unrolling
grad = [Theta1_grad(:) ; Theta2_grad(:)];

end

これで得られた $ J $ や $ grad $ を最急降下法を実行するライブラリに渡して、コストを最小化する $ \Theta $ を決定して完了です。

具体的な事例がないとわかりづらいですが、それはまた機会があれば。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up