More than 5 years have passed since last update.

機械学習を1ヵ月で実践レベルにする #2 (オンライン講座)

Last updated at 2017-01-10Posted at 2016-12-15

2日目です

今日の目標は、Coursera でStanford が提供しているMachine Learning の講座のWEEK 2 とWEEK 3 をやるということでした。

過去記事一覧

時間を見逃してた

毎日2WEEK ずつやるという目標でしたが、1WEEK あたりの時間がマチマチであることに気が付きました。そして特にこのWEEK 2, WEEK 3 は山場で、合わせると13時間以上かかることがわかります。

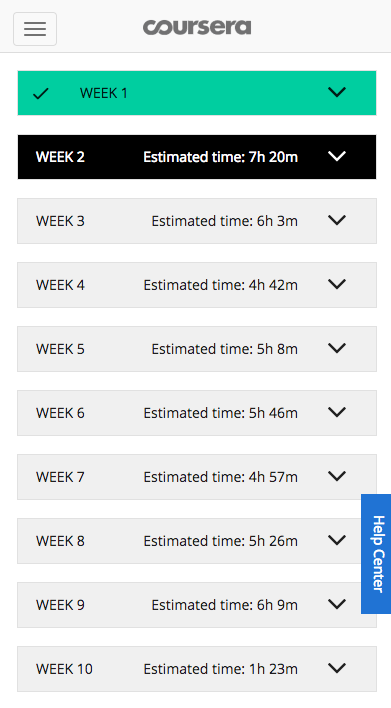
ということで早速目標の下方修正ですが、今日はWEEK2 を終わらせます。

Machine Learning (Coursera) WEEK 2

WEEK 2 のタイトル

Linear Regression with Multiple Variables
Octave/Matlab Tutorial

ということで、直訳すると「多変量の線形回帰」と「Octave/Matlab のチュートリアル」でしょうか。楽しみですね。ちなみにWEEK 1 の内容はまだどこにも書いていませんが、単一変数の線形回帰をひたすらやりました。線形回帰は誤解をおそれずにいうと、最小二乗法です。

最小二乗法は直感とも反しないので、割と簡単に理解できますし、少し難しいなと感じても、この講座がめちゃくちゃわかりやすいと思いますので大変おすすめです。

それではWEEK 2 のレポートです。

はじめに

まずはじめに、WEEK 1 でも絶賛していたOctave とMatlab 環境を用意するところから始まります。講座の中にインストールのチュートリアルまでついているので安心です。Ng 先生はやさしいです(講座の講師の方はAndrew Ng といいます)。Matlab は普通に手に入れようとすると結構高価だと聞いたことがあるのですが(本当？)、この講座経由で入れると、この講座での勉強用途に限られますが、無償で使わせていただけます。嬉しい！

Octave のインストールも丁寧に説明してくれているのですが、最後のほうに1行だけ

もしあなたがHomeBrew などのPackage Manager を使っているのなら、それらのPackage Manager からインストールすることをオススメします。
って書いてあるので要注意。完全にワナです。

なのでbrew でいれます。

brew cask install xquartz
brew tap homebrew/science
brew install octave

Octave などはいれるだけ入れて講義に戻ります

多変量による線形回帰
- 家の広さ、部屋数、階数などの多変量から、その家の売価予測をする
- WEEK 1 では家の広さからだけその家の売価予測をした
- 今回は多変量になるので、行列の計算が必要になる
多変量になっても基本的には「最急降下法」を使って目的関数を求める
- 学習係数αの取り方が重要
- αが小さいと、計算量(イテレーション数)が増えてしまう。
- αが大きいと、収束せずに発散してしまうことがある
- αを0.001 -> 0.003 -> 0.01 -> 0.03 -> 0.1 ... と変えて確認する
- (↑これはNg の経験則だが大抵うまくいくとのこと)
- 結果を画面にプロットしながら確認することで、Debug にもなるし他の示唆も得られる
- より効率よく計算するために、特徴量の数字のスケールを揃える(スケールフィッティングする)とよい
  - 最大値で割って0〜1の範囲に変換するのが簡単
  - 特徴量の平均との差をとって、範囲で割って、-1 〜 1の範囲に変換する方法も有効
一方、代数的に直接計算で求めることもできる
- octave であれば1行で計算できる
- しかし、特徴量 n が一般的に逆行列の計算が大変になり、遅くなる
- 特徴量 n の個数が1000個くらいなら十分に逆行列による計算でいける
- n が10,000を超えるようになると、最急降下法のほうが優れてくる
- また、他のアルゴリズムなどへの適用も最急降下法のほうが応用範囲が広い
- ごく限定された状態でのみ、代数的なアプローチが有効
- 代数的なアプローチの場合、特徴量のスケールフィッティングも不要
- 特徴量同士の間に線形な関係があると、計算過程ででてくる行列が非正則となり逆行列が計算出来ない場合がある。
- その場合、特徴量を正規化して、本来は特徴数を下げる必要があるが...
- これでも octave のpinv 関数であれば気にせず計算できる
Octave の使い方のレクチャー
- いろいろな言語で機械学習の講義を試してきた
  - C++, Java, Python, NumPy, R ...
  - その中でもOctave を使った場合が圧倒的に理解が速かった
  - 学習用としてはOctave (or Matlab)一択
- 業務の現場でも試作をOctave のような高級言語で行い
- 問題の本質を解くところに集中できるようにし
- 解決してから、プロダクトに載せるときに、もう少し低級な言語(java 等)にするのが良い
- プログラミングにかける時間は課題解決に掛ける時間としては無駄なので、まとまってから最後にJava で実装すればよい
- 結果的に時間の節約になる
- 試作用の言語として優れている
- MATLAB も良いが、少々高い
- R も悪くはない
- この講義の動画自体がOctave のチュートリアルとして優れている
- ともかく Octave 面白い。

レクチャービデオの途中に理解度を確認するための小クイズがあり、それに正解できると、自分が理解できているということがわかり安心できます。また、各章の最後にはちゃんとしたテストがあり、80% 以上の正答率を出さなければパスできません。8時間以内に3回しかチャレンジできないですし、チャレンジ毎に微妙に問題が変わるので、あてずっぽうで当たったところは同じ回答をして、間違えたところだけ直せば通るなんてこともできません。割としっかりと理解度を測れますし、ドキドキもします。

明日以降の目標

まず、Coursera の時間がある程度読めることがわかったので、Coursera 修了の目標を立ててしまいます。

12/16(金) WEEK 3 (6h3m)
12/17(土) WEEK 1 〜 WEEK 3 のReview とやり残し
12/19(月) WEEK 4 (4h42m)
12/20(火) WEEK 5 (5h8m)
12/21(水) WEEK 6 (5h46m)
12/22(木) WEEK 7 (4h57m)
12/23(金) WEEK 4 〜 WEEK 7 のReview とやり残し
12/26(月) WEEK 8 (5h26m)
12/27(火) WEEK 9 (6h9m)
12/28(水) WEEK 10, WEEK 11 (2h39m)
12/29(木) WEEK 8 〜 WEEK 11 のReview とやり残し

年内ギリギリですね...

また、 Coursera を1日1WEEK ずつにすると逆に少し時間に余裕が出てくるので、Cousera 以外の時間は機械学習でできることのアイデア出しや、実際にコードを書いて実践する練習などに当てる予定です。本格的なプロダクト改善に着手するのはちょうど年が明けてからになりそうです。

しばらくはこちらの連載(?)も、Coursera の Machine Learning の内容レポートになりそうです。

余談ですが、Coursera のコースは受講は無料で、受講後の修了証の発行に$79 がかかる仕組みでした。「修了証とかいらねーしwww」って思っていましたが、これだけ大変になると、ありがたみというか、御守り代わりに修了証ももらってもいいかもしれないなって思いました。この費目であれば、会社が出してくれる研修費で、大手を振って経費精算してくれそうですし。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up