対象者
活性化関数について、どんなものがあるのかまとめました。
最新のSwishとMish、さらにtanhExpも載せています!
一覧探してもなかなか良いの見つからないな〜という層をターゲットにしてます。
新しいのは見つけ次第追加します。
新しい関数の情報や、下記のTODOリストにある関数の情報をお持ちの方はぜひ教えてください!
勾配降下法もこちらでまとめています。
何かの役に立てばぜひLGTMやストック、コメントしていただけると励みになります!
更新履歴(2020/9/22~)
- 2020/9/22
- softmax関数の微分の修正
- softmin関数の微分の訂正とグラフの差し替え
- logSoftmax関数の微分の訂正
- バッチ法、ミニバッチ法に対応したコードに差し替え
メモリを犠牲に計算回数を削減する工夫をしてみました。有効かは未検証です。
- 2020/9/23
- 効果がほぼなかったので修正
- 2020/9/27
- hardSwish関数を追加
-
_act_dicとget_act関数の実装を少し修正し、入力の自由度を向上させました。
- 2020/10/20
- ACON関数の情報を追加
- 実装はしばしお待ちください...
- 2020/10/21
- ACON関数の情報をちょっと修正
- ACON関数の実装を追加
- ただしハイパーパラメータの学習については実装してみましたが動作未確認です。
- いずれ動くかどうか確認します。
TODOリスト
- hardShrink関数の補足情報を調べる
- softShrink関数の補足情報を調べる
- Threshold関数の補足情報を調べる
- logSigmoid関数の補足情報を調べる
- tanhShrink関数の補足情報を調べる
- hardtanh関数の補足情報を調べる
- ReLU6関数の補足情報を調べる
- CELU関数の補足情報を調べる
- softmin関数の補足情報を調べる
- logSoftmax関数の補足情報を調べる
- 未実装のいくつかの関数について調べる
- Pytorch
- MultiheadAttention関数とは
- PReLU関数の学習メソッド
- RReLU関数の実装
- GELU関数に出てくる累積分布関数とは?
- GELU関数の実装
- Softmax2d関数の実装
- Pytorch
目次
- ステップ関数(step)
- 恒等関数(identity)
- Bent Identity関数
- hardShrink関数
- softShrink関数
- Threshold関数
- シグモイド関数(sigmoid)
- hardSigmoid関数
- logSigmoid関数
- tanh関数
- tanhShrink関数
- hardtanh関数
- ReLU関数
- ReLU6関数
- leaky-ReLU関数
- ELU関数
- SELU関数
- CELU関数
- ソフトマックス関数(softmax)
- softmin関数
- logSoftmax関数
- softplus関数
- softsign関数
- Swish関数
- hardSwish関数
- ACON関数
- Mish関数
- tanhExp関数
- コード例
ステップ関数(step)
まずはステップ関数から。もっとも歴史ある活性化関数でしょう。
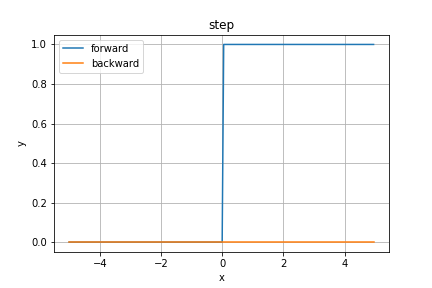
当時はパーセプトロンの実装に用いられていましたが、昨今の深層学習ではまず見かけません。
その理由は微分が($x \ne 0$の)全ての実数で$0$となるため、誤差逆伝播によるパラメータの最適化ができないためですね。
順伝播の数式は
y = \left\{
\begin{array}{cc}
1 & (x \gt 0) \\
0 & (x \le 0)
\end{array}
\right.
こんな感じで、逆伝播の数式は当然ですが
\cfrac{\partial y}{\partial x} = 0 \quad (x \ne 0)
となり、これを流れてきた誤差に乗算します。つまり何も流しません。
このため、誤差逆伝播法を適用できず、深層学習においては日陰に追いやられることになりました。
恒等関数(Identity)
恒等関数は入力をそのまま出力します。回帰分析の出力層の活性化関数に使われますね。中間層での出番はありません。
わざわざこのような活性化関数を使うのは一意的に実装するためです。一意的な実装とは、ここでは条件分岐などで処理をわけないことを意図しています。
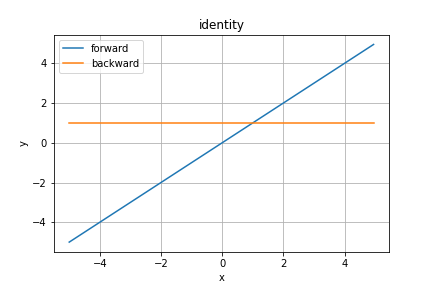
微分値は$1$なので誤差がそのまま前の層へ伝播します。誤差計算は二乗誤差を用いるので次の層への伝播は$y - t$になりますね〜
順伝播の数式は
y = x
で、逆伝播は
\cfrac{\partial y}{\partial x} = 1
となります。流れてきたそのままの値を流すことになることが確認できますね!
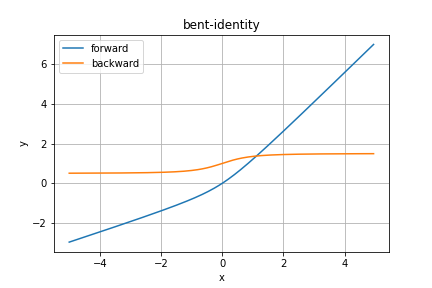
Bent Identity関数
Identity関数と類似の関数です。
ただし直線的ではなく少し曲がっているのが特徴です。
順伝播の数式は
y = \cfrac{1}{2}(\sqrt{x^2 + 1} - 1) + x
こんな感じで、逆伝播は
\cfrac{\partial y}{\partial x} = \cfrac{x}{2 \sqrt{x^2 + 1}} + 1
となります。なんとなくReLU関数っぽい(個人の感想です)。
日本語で紹介してる記事はぱっと見で探したところ見つからなかったのでマイナーな活性化関数なのかなと思います。
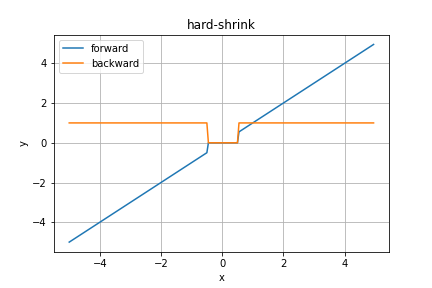
hardShrink関数
Pytorchより、とりあえず紹介だけです。
TODO 補足情報を調べる
順伝播の数式は
y = \left\{
\begin{array}{cc}
x & (x \lt -\lambda \quad \textrm{or} \quad \lambda \lt x) \\
0 & (\textrm{otherwise})
\end{array}
\right.
で、逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
1 & (x \lt -\lambda \quad \textrm{or} \quad \lambda \lt x) \\
0 & (\textrm{otherwise})
\end{array}
\right.
となります。$\lambda$のデフォルト値は$0.5$です。
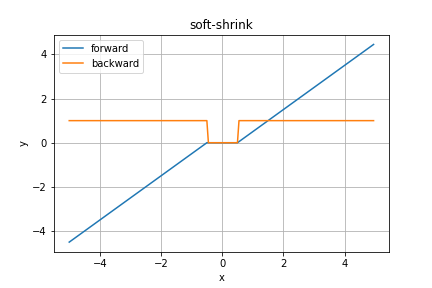
softShrink関数
Pytorchより、こちらも紹介だけ。
TODO 補足情報を調べる
順伝播の数式は
y = \left\{
\begin{array}{cc}
x + \lambda & (x \lt -\lambda) \\
x - \lambda & (x \gt \lambda) \\
0 & (\textrm{otherwise})
\end{array}
\right.
で、逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
1 & (x \lt -\lambda \quad \textrm{or} \quad \lambda \lt x) \\
0 & (\textrm{otherwise})
\end{array}
\right.
となります。こちらの$\lambda$の初期値も$0.5$ですね。
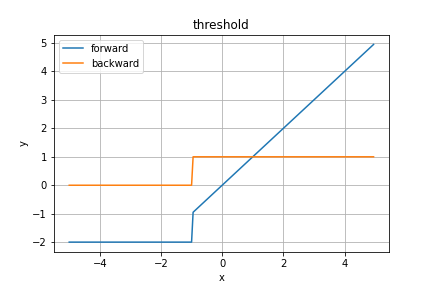
Threshold関数
Pytorchより、これまた紹介だけです。
TODO 補足情報を調べる
順伝播の数式は
y = \left\{
\begin{array}{cc}
x & (x \gt threshold) \\
value & (\textrm{otherwise})
\end{array}
\right.
で、逆伝播は
y = \left\{
\begin{array}{cc}
1 & (x \gt threshold) \\
0 & (\textrm{otherwise})
\end{array}
\right.
となります。ここで、変数$threshold$と$value$は事前に与えられるべき値です。グラフではとりあえず適当に
threshold = -1 \\
value = -2
としています。
シグモイド関数(sigmoid)
シグモイド関数は誤差逆伝播法が登場した頃によく使用されていた活性化関数ですね。しかし今は中間層に使われることは少なく、2値分類問題の出力層に使われることが多いですね。
理由は後述のデメリットのためです。
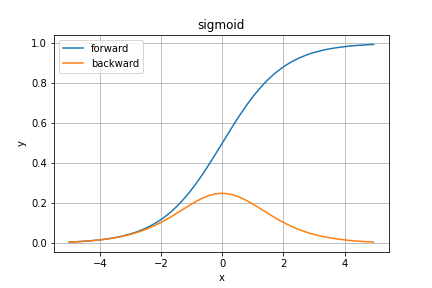
順伝播は
y = \cfrac{1}{1 + e^{-x}}
逆伝播は
\cfrac{\partial y}{\partial x} = y(1 - y)
のように書くことができます。
微分を出力から簡単に求められることが最大の特徴ですが、極端に大きい・小さい入力に対しての応答が悪いことや、微分の最大値が$0.25$であるために層を重ねると勾配消失の問題が起こるなどのデメリットもあります。
あと指数計算と割り算があるため、ReLU関数などのシンプルな関数と比べてどうしても計算負荷が高くなります。
hardSigmoid関数
シグモイド関数を1次関数などの直線で近似したものがhardSigmoid関数です。
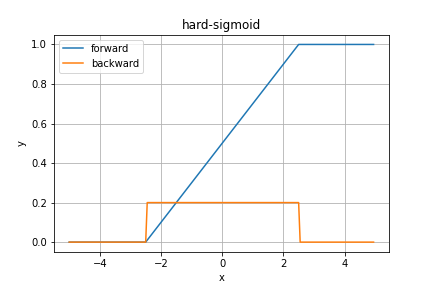
数式的には、順伝播は
y = \left\{
\begin{array}{cc}
1 & (x \gt 2.5) \\
0.2x + 0.5 & (-2.5 \le x \le 2.5) \\
0 & (x \lt -2.5)
\end{array}
\right.
逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
0.2 & (-2.5 \le x \le 2.5) \\
0 & (\textrm{otherwise})
\end{array}
\right.
のようになります。
詳しく検証している記事があるので、もっと知りたい方はそちらへどうぞ!
1次関数の係数が$0.2$であることにこんな複雑な理論的理由があるなんて...
読んだけどさっぱりわかりませんでした
logSigmoid関数
これもPytorchより、紹介だけです。sigmoid関数の対数を取ります。
TODO 補足情報を調べる
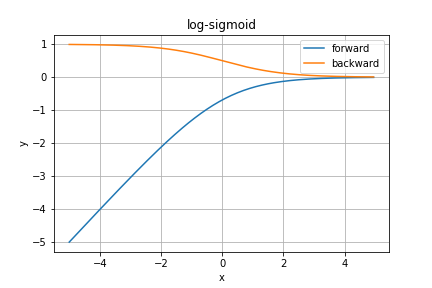
順伝播の数式は
y = \log \left( \cfrac{1}{1 + e^{-x}} \right)
となり、逆伝播は
\cfrac{\partial y}{\partial x} = \cfrac{1}{1 + e^x}
となります。逆伝播の分母は$-x$乗ではないので注意してください。
tanh関数
sigmoid関数の微分の最大値が$0.25$であるという弱点を解決する関数の一つとして提案されたのが双曲線関数の一つであるtanh関数です。
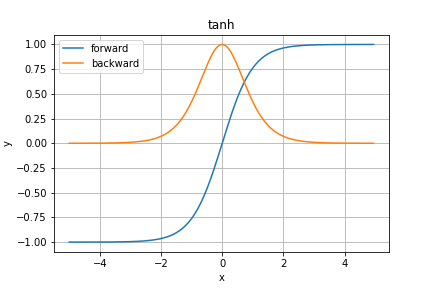
図を見ての通り、微分の最大値が$1$となり、勾配消失の原因を取り除くことができました。
しかし、依然として極端に大きい・小さい入力での微分が$0$となってしまう問題は残っています。
y = \tanh x = \cfrac{e^x - e^{-x}}{e^x + e^{-x}}
逆伝播は
\cfrac{\partial y}{\partial x} = \textrm{sech}^2 x = \cfrac{1}{\cosh^2 x} = \cfrac{4}{(e^x + e^{-x})^2}
となります。
最近Mish関数やtanhExp関数などの期待の新星に一部使われてますね〜注目度が高い関数みたいです。
tanhShrink関数
これもPytorchより。紹介だけです。
TODO 補足情報を調べる
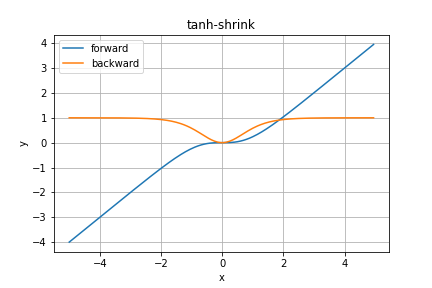
順伝播の数式は
y = x - \tanh x
で、逆伝播は
\cfrac{\partial y}{\partial x} = \tanh^2 x
となります。
hardtanh関数
これもPytorchです。紹介だけ...
TODO 補足情報を調べる
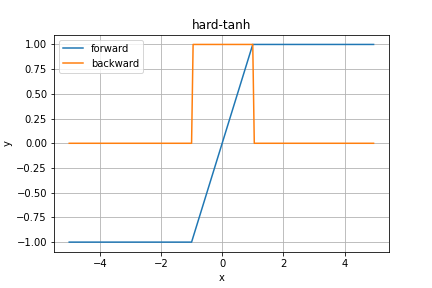
順伝播の数式は
y = \left\{
\begin{array}{cc}
1 & (x \gt 1) \\
-1 & (x \lt -1) \\
x & (\textrm{otherwise})
\end{array}
\right.
で、逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
0 & (x \lt -1 \quad \textrm{or} \quad 1 \le x) \\
1 & (\textrm{otherwise})
\end{array}
\right.
となります。
ReLU関数
ReLU関数(一般にランプ関数と呼ばれているそうです)は結構最近に提案されて覇権を握っている活性化関数です。その特徴はなんと言ってもそのシンプルで高速な演算ですね。
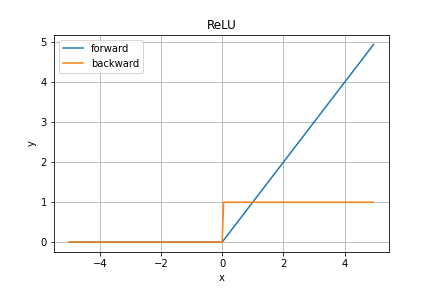
順伝播の数式は
y = \left\{
\begin{array}{cc}
x & (x \gt 0) \\
0 & (x \le 0)
\end{array}
\right.
逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
1 & (x \gt 0) \\
0 & (x \le 0)
\end{array}
\right.
となります。入力が正の値だと勾配は常に$1$となるので勾配消失が起こりにくく、層を重ねやすいというメリットがありますが、負の入力に対しては一切学習が進まないというデメリットもあります。
また、$x=0$で不連続微分不可能であることを基本的に無視しています。
誤差逆伝播法では連鎖律を用いた勾配の伝播を元に学習を進めるため、本来であれば活性化関数は全ての実数で微分可能であるべきですが、実際のところピッタリ$x=0$となる場合の方が少ない&どうせ$0$なので問題になっていません。
ReLU6関数
Pytorchより、紹介だけです。
TODO 補足情報を調べる
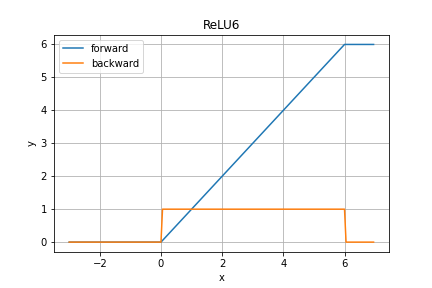
順伝播の数式は
y = \left\{
\begin{array}{cc}
0 & (x \le 0) \\
6 & (x \ge 6) \\
x & (\textrm{otherwise})
\end{array}
\right.
となり、逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
0 & (x \le 0 \quad \textrm{or} \quad 6 \le x) \\
1 & (\textrm{otherwise})
\end{array}
\right.
となります。
leaky-ReLU関数
leaky-ReLU関数はReLU関数の「負の入力に対しては学習が進まない」という欠点を補うべく、負の入力の時はごく小さな傾きの1次関数を出力するようにしたものです。
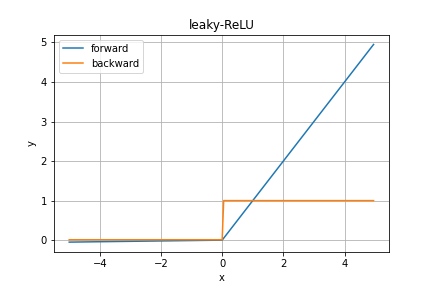
グラフではほとんど分かりませんが、数式では
y = \left\{
\begin{array}{cc}
x & (x \gt 0) \\
0.01x & (x \le 0)
\end{array}
\right.
のように、負の入力の時の出力が異なります。そのため、逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
1 & (x \gt 0) \\
0.01 & (x \le 0)
\end{array}
\right.
となります。これもやっぱり$x=0$で不連続微分不可能です。
また、調べてる中で色々なところで見かけたのですが、どうやらこの関数の命名者が「特にこれを使う意味はなかった」と言っているようです。ちょっと意外ですね。少しは改善されそうなのに...
ELU関数
ReLU関数とよく似た形をしたグラフで、$x=0$の時により滑らかな関数の一つにELU関数というものがあります。
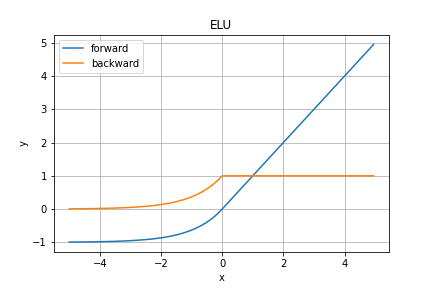
y = \left\{
\begin{array}{cc}
x & (x \ge 0) \\
\alpha (e^x - 1) & (x \lt 0)
\end{array}
\right.
となり、逆伝播は
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
1 & (x \ge 0) \\
\alpha e^x & (x \lt 0)
\end{array}
\right.
となります。
$\alpha$の値は次のSELU関数で理論的に適切な値を取ることが多いみたいです(多分)。
2020/6/2修正
$\alpha$のデフォルト値は大抵$1$のようです。$\alpha=1$のグラフに差し替えさせていただきます。
誤った情報を発信してしまい申し訳ありませんでした...
SELU関数
ELU関数の出力を$\lambda$倍したのがSELU関数です。
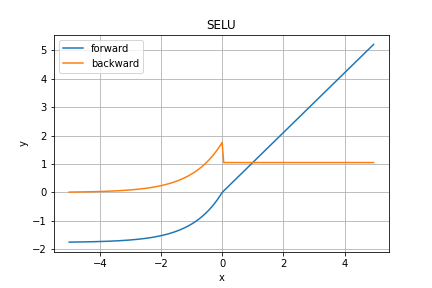
数式では
y = \left\{
\begin{array}{cc}
\lambda x & (x \ge 0) \\
\lambda \alpha (e^x - 1) & (x \lt 0)
\end{array}
\right.
であり、逆伝播も
\cfrac{\partial y}{\partial x} = \left\{
\begin{array}{cc}
\lambda & (x \ge 0) \\
\lambda \alpha e^x & (x \lt 0)
\end{array}
\right.
のように$\lambda$倍されます。
理論的に最適なパラメータ値が求まるらしく、その値が
\alpha = 1.67326\ldots, \quad \lambda = 1.0507\ldots
となるようです。そのうち論文読むかも...読んだら補足します。
CELU関数
こちらもPytorchより、紹介のみです。
TODO 補足情報を調べる
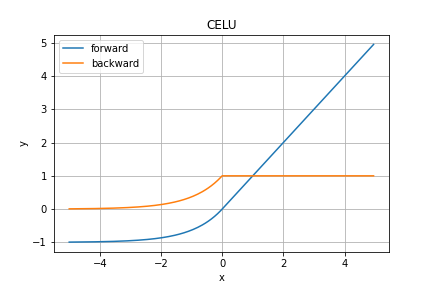
順伝播の数式は
y = \left\{
\begin{array}{cc}
x & (x \ge 0) \\
\alpha \left( e^{\frac{x}{\alpha}} - 1 \right) & (\textrm{otherwise})
\end{array}
\right.
で、逆伝播の数式は
y = \left\{
\begin{array}{cc}
1 & (x \ge 0) \\
e^{\frac{x}{\alpha}} & (\textrm{otherwise})
\end{array}
\right.
となります。
ソフトマックス関数(softmax)
ソフトマックス関数は多値分類問題の出力層の活性化関数として用いられます。
その計算の特性上出力を確率として見なすことが可能です。
また、sigmoid関数の拡張版の関数となっています。
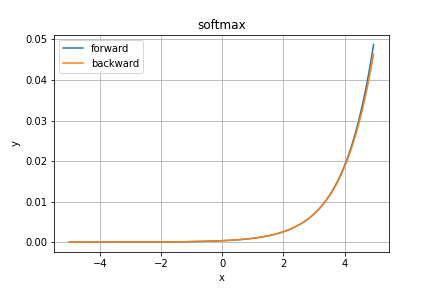
グラフの縦軸はあまり気にしないでOKです。重要なのは積分する(コンピュータは離散的なので総和を取る)と$1$になるということだけです。
数式的には
y_i = \cfrac{e^{x_i}}{\displaystyle\sum_{k=1}^{n}{e^{x_k}}} \quad (i = 1, 2, \ldots, n)
という感じですね。逆伝播は一応
\left( \cfrac{\partial y}{\partial x} \right)_i = \sum_{j=1}^{n}{\cfrac{\partial y_j}{\partial x_i}} = \sum_{j=1}^{n}{\left\{ \begin{align}
e^{x_i} \cfrac{\displaystyle\sum_{k=1}^{n}{e^{x_k}} - e^{x_j}}{\left( \displaystyle\sum_{k=1}^{n}{e^{x_k}} \right)^2} &= y_i (1 - y_j) & (j = i) \\
-\cfrac{e^{x_i} e^{x_j}}{\left( \displaystyle\sum_{k=1}^{n}{e^{x_k}} \right)^2} &= -y_i y_j & (j \ne i)
\end{align}\right\} } = y_i (1 - y_i) - \sum_{j=1, j \ne i}^{n}{y_i y_j} = \sum_{j=1}^{n}{y_i(\delta_{ij} - y_j)}
となります。$\delta_{ij}$はDiracのデルタ関数です。
こうしてみるとsigmoid関数の拡張系であるということに納得しやすいですね。
\delta_{ij} = \left\{ \begin{align}
1 && (i = j) \\
0 && (i \ne j)
\end{align} \right.
また、交差エントロピー誤差
Error = t \log y
を取ることで、出力層から中間層への逆伝播が
y - t
という非常にシンプルなものになります。
ちなみにこれは偶然ではなく、交差エントロピー誤差というものはsoftmax関数にフィッティングして、勾配が$y - t$となるようわざわざ設計された関数です。
いつか計算グラフで紹介するかもしれません。ここで紹介しています。
softmin関数
これもPytorchより。softmax関数の逆で、小さい値の確率が大きくなります。
TODO 補足情報を調べる
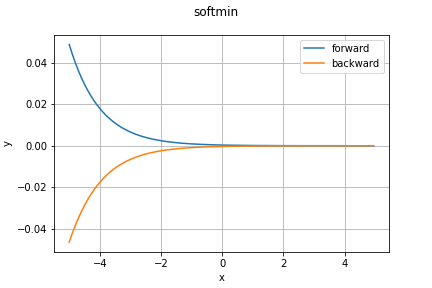
順伝播の数式は
y_i = \cfrac{e^{-x_i}}{\displaystyle\sum_{k=1}^{n}{e^{-x_k}}} \quad (i = 1, 2, \ldots, n)
で、逆伝播の数式は
\left( \cfrac{\partial y}{\partial x} \right)_i = \sum_{j=1}^{n}{\cfrac{\partial y_j}{\partial x_i}} = \sum_{j=1}^{n}{\left\{ \begin{align}
-e^{-x_i} \cfrac{\displaystyle\sum_{k=1}^{n}{e^{-x_k}} - e^{-x_j}}{\left( \displaystyle\sum_{k=1}^{n}{e^{-x_k}} \right)^2} &= - y_i (1 - y_j) & (j = i) \\
-\cfrac{e^{-x_i} \times (-e^{-x_j})}{\left( \displaystyle\sum_{k=1}^{n}{e^{-x_k}} \right)^2} &= y_i y_j & (j \ne i)
\end{align}\right\} } = - y_i (1 - y_i) + \sum_{j=1, j \ne i}^{n}{y_i y_j} = - \sum_{j=1}^{n}{y_i(\delta_{ij} - y_j)}
となります。こちらも交差エントロピー誤差を用いれば綺麗に誤差が逆伝播するんでしょうか...今度調べてみます。
logSoftmax関数
Pytorchより、こちらはsoftmax関数の対数をとったものです。
TODO 補足情報を調べる
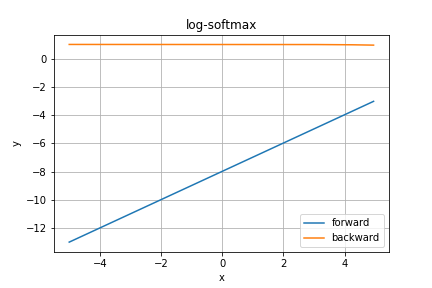
ほぼ直線に見えますね。合ってるんでしょうか...一応コードは合ってると思ってます。
順伝播の数式は
y_i = \log \left( \cfrac{e^{x_i}}{\displaystyle\sum_{k=1}^{n}{e^{x_k}}} \right)
で、逆伝播は
\left( \cfrac{\partial y}{\partial x} \right)_i = \sum_{j=1}^{n}{\cfrac{\partial y_j}{\partial x_i}} = \sum_{j=1}^{n}{\left\{ \begin{align}
\cfrac{e^{x_i}\cfrac{\displaystyle\sum_{k=1}^{n}{e^{x_k}} - e^{x_j}}{\left( \displaystyle\sum_{k=1}^{n}{e^{x_k}} \right)^2}}{\cfrac{e^{x_i}}{\displaystyle\sum_{k=1}^{n}{e^{x_k}}}} &= 1 - e^{y_j} & (j = i) \\
\cfrac{\cfrac{-e^{x_i}e^{x_j}}{\left( \displaystyle\sum_{k=1}^{n}{e^{x_k}} \right)^2}}{\cfrac{e^{x_i}}{\displaystyle\sum_{k=1}^{n}{e^{x_k}}}} &= - e^{y_j} & (j \ne i)
\end{align}\right\} } = 1 - e^{y_i} - \sum_{j=1, j \ne i}^{n}{e^{y_j}} = \sum_{j=1}^{n}{(\delta_{ij} - e^{y_j})}
となります。
softplus関数
softplus関数はsoftmax関数と似た名前ですが、本質はReLU関数に似ています。
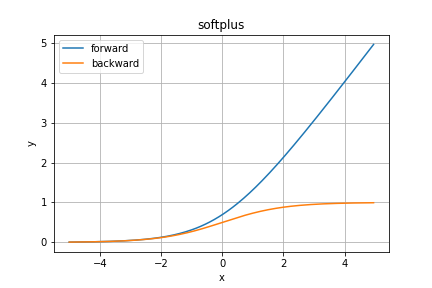
数式では
y = \log{(1 + e^x)} = \ln{(1 + e^x)}
と表され、逆伝播は
\cfrac{\partial y}{\partial x} = \cfrac{e^x}{1 + e^x} = \cfrac{1}{1 + e^{-x}}
のようになります。ReLU関数と微分も含めて見た目そっくりですね。
ちなみに、$\ln x$とは底がネイピア数の対数関数であることを明示するためのものです。つまり
\ln x = \log_ex
ということですね。
softsign関数
こちらも名前こそsoftmax関数と似ていますが、実際はtanh関数に似ています。
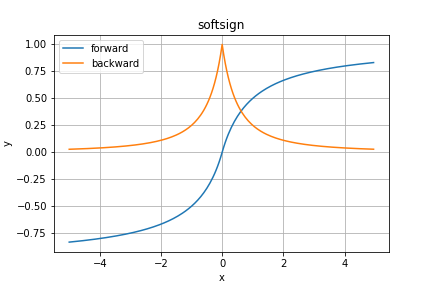
順伝播の見た目はtanh関数そっくりですが、逆伝播が全く異なりますね。すごく尖ってます。
順伝播を数式で見ると
y = \cfrac{x}{1 + |x|}
となり、逆伝播は
\cfrac{\partial y}{\partial x} = \cfrac{1}{(1 + |x|)^2}
となっています。$x=0$で微分が不連続関数になってしまっていますね。
2020/6/2修正
関数の連続性を勘違いしていました。正しくは不連続ではありません。微分不可能です。
\lim_{x \to \pm 0}{\cfrac{1}{(1 + |x|)^2}} = 1
\Leftrightarrow
\lim_{x \to 0}{\cfrac{1}{(1 + |x|)^2}} = 1
であり、
\cfrac{\partial y}{\partial x} = \cfrac{1}{(1 + |0|)^2} = 1 \quad (\because x = 0)
なので、
\lim_{x \to 0}{\cfrac{1}{(1 + |x|)^2}} = \cfrac{1}{(1 + |0|)^2}
となり、連続であることが示されます。
Swish関数
こちらは2017年登場の、ReLU関数の後継と期待されているSwish関数です。
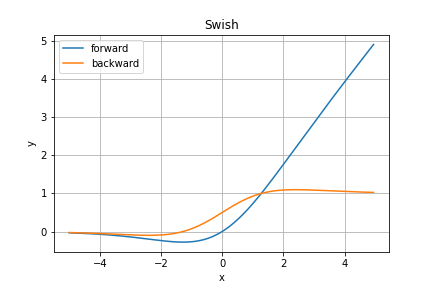
見た目もReLU関数とそっくりですが、ELU関数やSELU関数とは異なり、$x=0$でも連続な微分可能な関数となっています。
さらに$C^{\infty}$級の関数であるのも特徴です。
さらにさらに、負の入力に対して負の値をわずかに取ることも分かります。最小値ありの最大値なしというのが嬉しい点(らしい)です。
順伝播を数式で表すと
y = x \sigma_{sigmoid}(\beta x) = \cfrac{x}{1 + e^{-\beta x}}
という感じですね。上のグラフでは$\beta=1$と設定しています。
ちなみに$\beta$は誤差逆伝播法で最適化できるそうです(未実装)。
逆伝播は
\cfrac{\partial y}{\partial x} = \beta y + \sigma_{sigmoid}(\beta x)(1 - \beta y) = \beta y + \cfrac{1 - \beta y}{1 + e^{-\beta x}}
のように書けます。sigmoid関数の面影が垣間見える感じですね。
hardSwish関数
こちらは@tsubota-kougaさんより情報をいただいたhardSwish関数です!
論文はそのうち読みます...
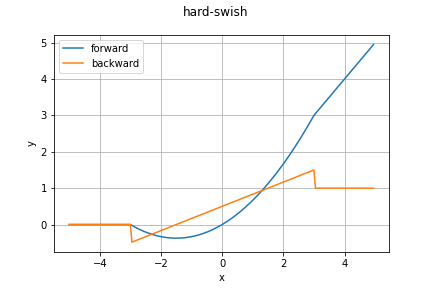
Swish関数はsigmoid関数が使用されているため、つまり指数計算があるため計算量が多くなっていましたが、こちらはReLU6関数を利用してsigmoid関数を$-3 \le x \le 3$の範囲で近似するようになっています。
y = x\cfrac{\sigma_{ReLU6}(x+3)}{6}
= \left\{ \begin{align}
0 && (x \le -3) \\
\cfrac{x(x+3)}{6} && (-3 \le x \le 3) \\
x && (3 \le x)
\end{align} \right.
ReLU6関数に投げる値が$+3$されているため、範囲が$-3 \le x \le 3$となっています。逆伝播は
\cfrac{\partial y}{\partial x} = \left\{ \begin{align}
0 && (x \le 3) \\
\cfrac{2x + 3}{6} && (-3 \le x \le 3) \\
1 && (3 \le x)
\end{align} \right.
で計算できます。
Swish関数と比べてみましょう。
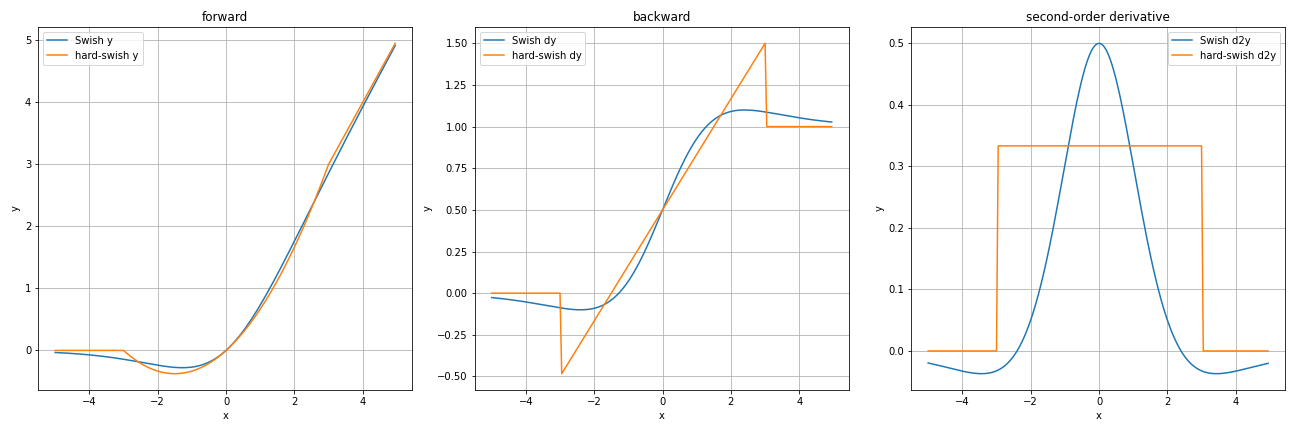
Swish関数をそれなりに近似できてる感はありますね。でももう少し近づけられそうな気がしないでもない...
ACON関数
こちらはhardSwish関数の情報をくださった@tsubota-kougaさんより情報をいただいたACON関数です!
簡単に論文をまとめていきます。それでも他の関数と比較すると圧倒的に長くなりますがご了承ください。
やっぱ長いので詳細は折り畳んでおきます。
論文詳細
ACON: ACtivate Or Notそのものは関数というよりアルゴリズムの方が近いかもしれません。というのも、ACONはその名の由来通りニューロンを活性化するかしないかを明示的に学習することを意図して導入された考え方だからです。論文の大筋としては
- Swish関数がReLUの自然な拡張であるとする
- ReLUファミリーをReLU-Swish拡張と同じように拡張し、ACONファミリーとして提案する
- 明示的にニューロンの活性/非活性スイッチを学習するmeta-ACON関数を提案する
S_{\max}(x_1, \ldots, x_n) = \cfrac{\displaystyle\sum_{i=1}^{n}{x_i e^{\beta x_i}}}{\displaystyle\sum_{i=1}^{n}{e^{\beta x_i}}}
\begin{align}
S_{\max}(\eta_l(x), \eta_r(x)) &= \eta_l(x) \cfrac{e^{\beta \eta_l(x)}}{e^{\beta \eta_l(x)} + e^{\beta \eta_r(x)}} + \eta_r(x) \cfrac{e^{\beta \eta_r(x)}}{e^{\beta \eta_l(x)} + e^{\beta \eta_r(x)}} = \eta_l(x) \cfrac{1}{1 + e^{- \beta (\eta_l(x)-\eta_r(x))}} + \eta_r(x) \cfrac{1}{1+e^{\beta (\eta_l(x)-\eta_r(x))}} \\
&= \eta_l(x) \sigma(\beta(\eta_l(x) - \eta_r(x))) + \eta_r(x) \left\{1 - \cfrac{1}{1+e^{-\beta (\eta_l(x)-\eta_r(x))}}\right\} \\
&= (\eta_l(x) - \eta_r(x))\sigma(\beta (\eta_l(x) - \eta_r(x))) + \eta_r(x)
\end{align}
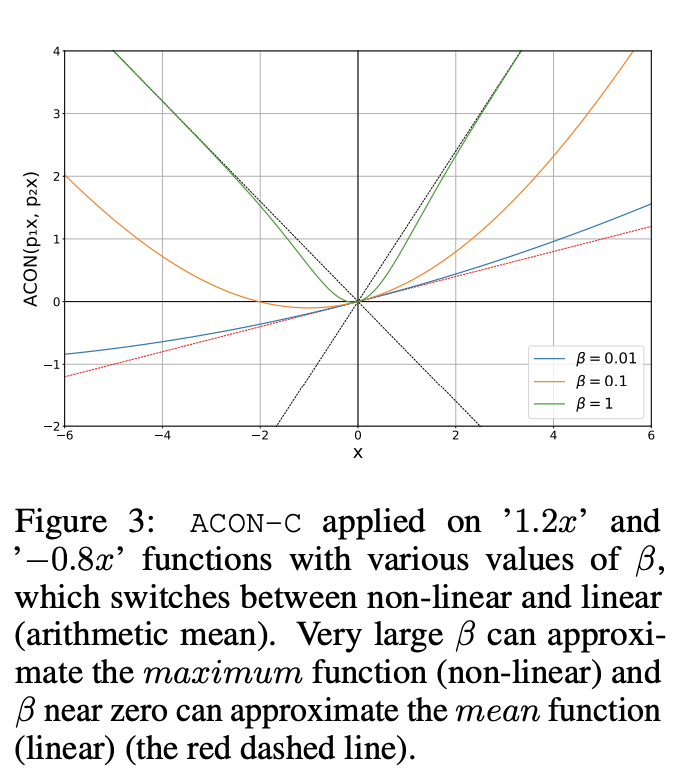
\sigma_{\textrm{ACON-B}}(x) = (1-p)x \sigma(\beta (1-p)x) + px
\sigma_{\textrm{ACON-C}}(x) = (p_1-p_2)x \sigma(\beta (p_1-p_2)x) + p_2 x
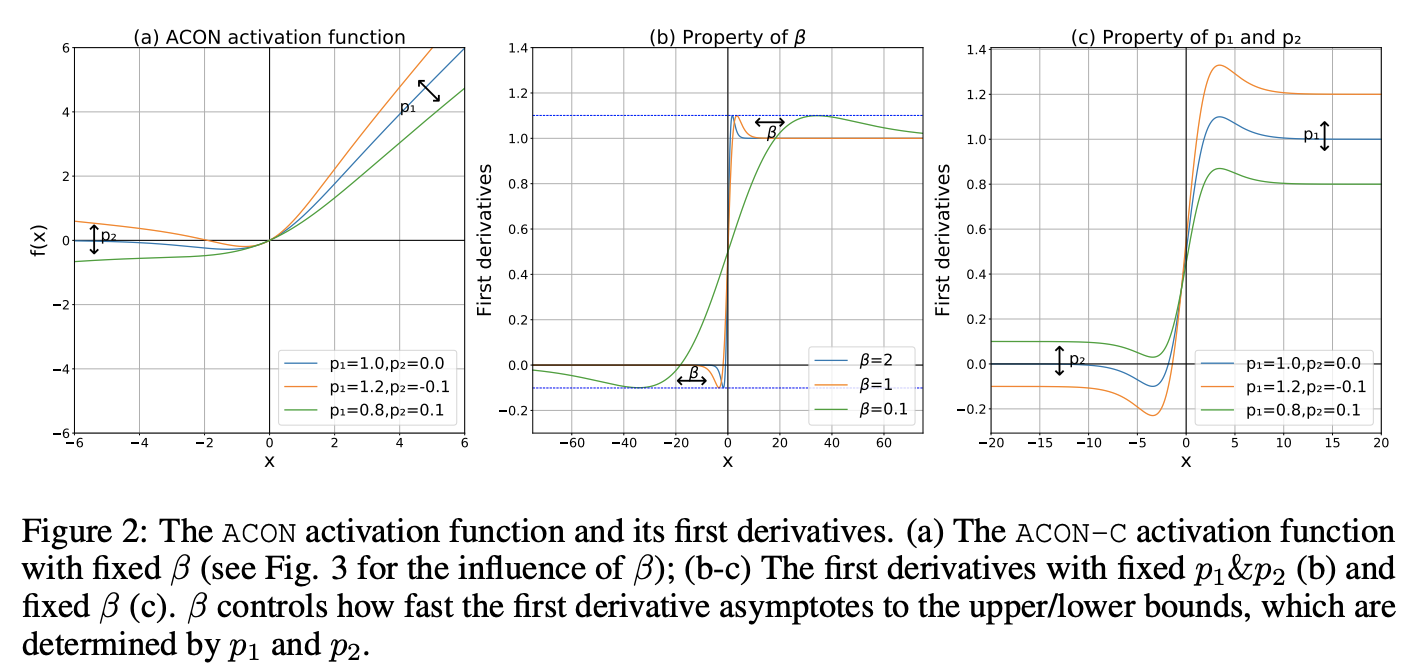
\cfrac{\partial \sigma_{\textrm{ACON-C}}(x)}{\partial x} = \cfrac{(p_1 - p_2)\left( 1 + e^{-\beta (p_1 - p_2)x} \right) + \beta (p_1-p_2)^2 e^{-\beta (p_1 - p_2)x}x}{\left(1 + e^{-\beta (p_1 - p_2)x} \right)^2} + p2 \\
\lim_{x \to \infty}{\cfrac{\partial \sigma_{\textrm{ACON-C}}(x)}{\partial x}} = p_1, \quad \lim_{x \to -\infty}{\cfrac{\partial \sigma_{\textrm{ACON-C}}(x)}{\partial x}} = p_2 \qquad (\beta \gt 0)
meta-ACON
\beta = G(x)
\begin{align}
\beta &= G(x) = \sigma \left( \sum_{c=1}^{C}{\sum_{h=1}^{H}{\sum_{w=1}^{W}{x_{c, h, w}}}} \right) = \sigma \left( \sum_{c=1}^{C}{HW\textrm{GAP}(x_c)} \right) && (\textrm{レイヤで共通のスイッチ}) \\
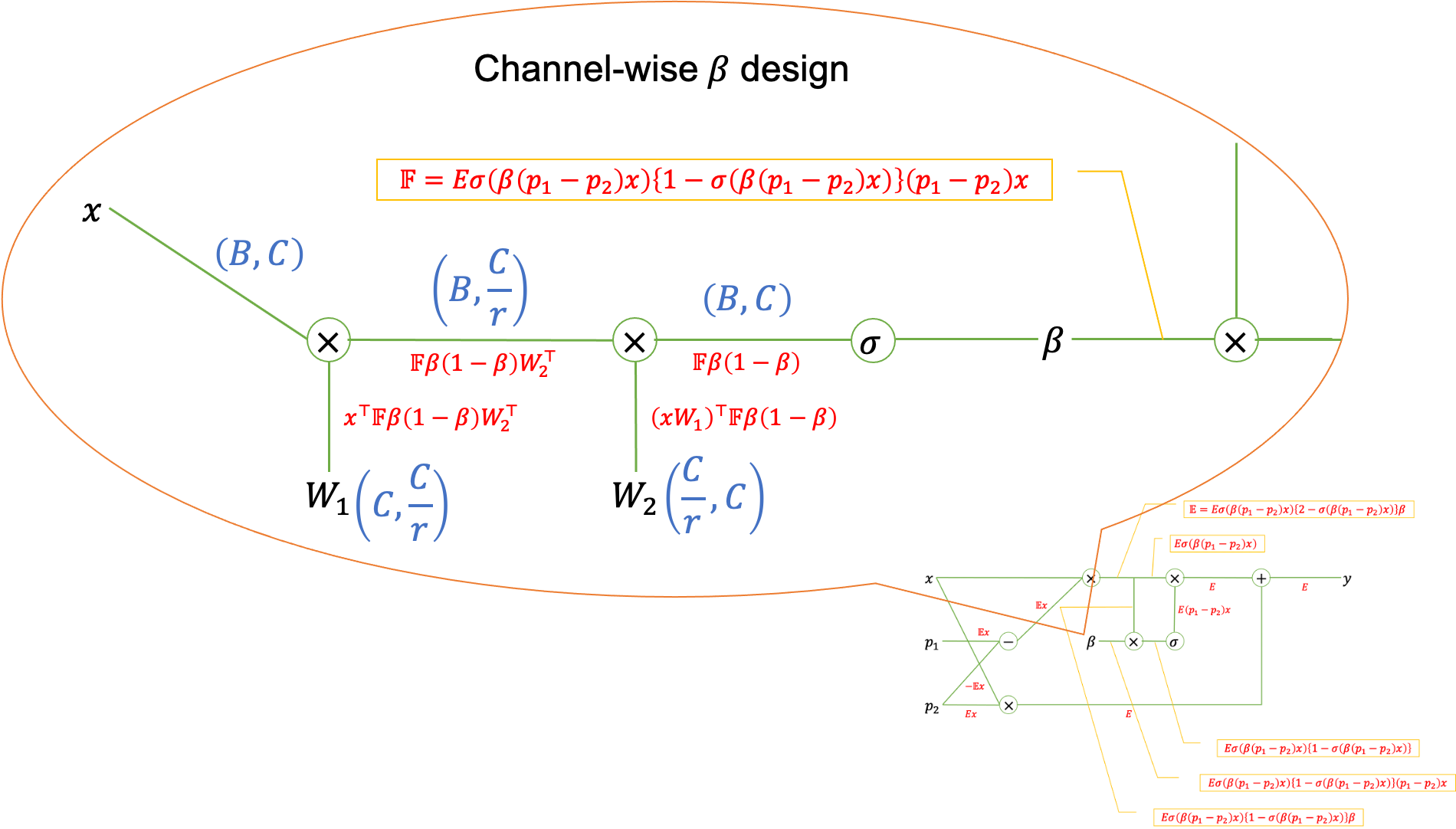
\beta_c &= G(x_c) = \sigma \left( W_1 W_2 \sum_{h=1}^{H}{\sum_{w=1}^{W}{x_{c, h, w}}} \right) = \sigma \left( fc[fc[HW\textrm{GAP}(x_c)]] \right) && (\textrm{チャンネルで共通のスイッチ}, W_1 \in \mathbb{R}^{C \times C/r}, W_2 \in \mathbb{R}^{C/r \times C}, fc[•]\textrm{は全結合層}) \\
\beta_{c, h, w} &= G(x_{c, h, w}) = \sigma (x_{c, h, w}) && (ニューロン固有のスイッチ)
\end{align}
必要なところだけ纏めると、順伝播は学習可能なハイパーパラメータ$\beta, p_1, p_2$を用いて
\sigma_{\textrm{ACON-C}}(x) = (p_1-p_2)x \sigma(\beta (p_1-p_2)x) + p_2 x
と表され、逆伝播は
\cfrac{\partial \sigma_{\textrm{ACON-C}}(x)}{\partial x} = \cfrac{(p_1 - p_2)\left( 1 + e^{-\beta (p_1 - p_2)x} \right) + \beta (p_1-p_2)^2 e^{-\beta (p_1 - p_2)x}x}{\left(1 + e^{-\beta (p_1 - p_2)x} \right)^2} + p2
と表されます。ちなみに$\beta$は
\begin{align}
\beta &= G(x) = \sigma \left( \sum_{c=1}^{C}{\sum_{h=1}^{H}{\sum_{w=1}^{W}{x_{c, h, w}}}} \right) = \sigma \left( \sum_{c=1}^{C}{HW\textrm{GAP}(x_c)} \right) && (\textrm{レイヤで共通のスイッチ}) \\
\beta_c &= G(x_c) = \sigma \left( W_1 W_2 \sum_{h=1}^{H}{\sum_{w=1}^{W}{x_{c, h, w}}} \right) = \sigma \left( fc[fc[HW\textrm{GAP}(x_c)]] \right) && (\textrm{チャンネルで共通のスイッチ}, W_1 \in \mathbb{R}^{C \times C/r}, W_2 \in \mathbb{R}^{C/r \times C}, fc[•]\textrm{は全結合層}) \\
\beta_{c, h, w} &= G(x_{c, h, w}) = \sigma (x_{c, h, w}) && (ニューロン固有のスイッチ)
\end{align}
が論文では提案されていますが、実際はデザイナブルです。
また、$\beta, p_1, p_2$への誤差の逆伝播は計算グラフを用いると次のように計算されることがわかります。
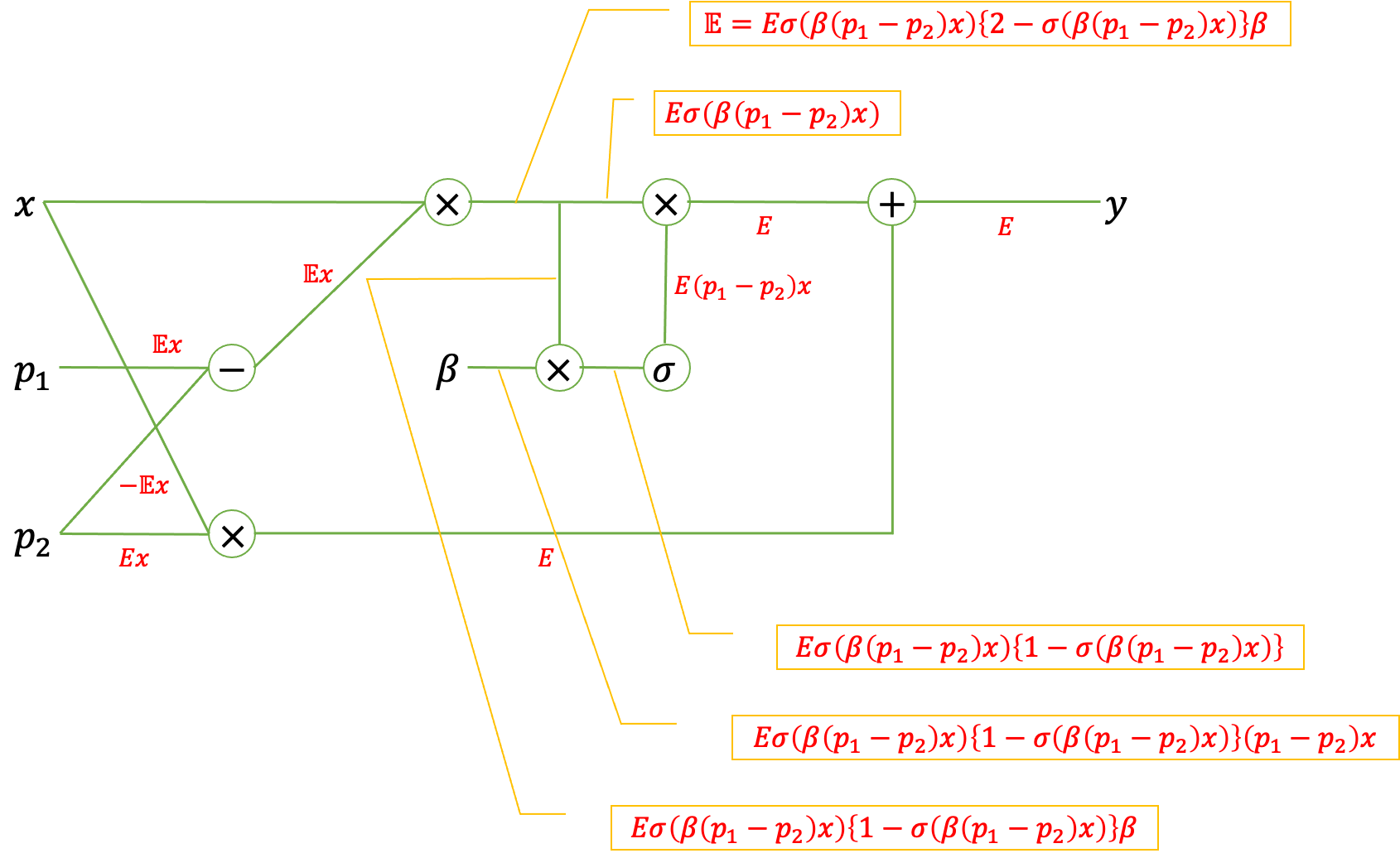
\begin{align}
\cfrac{\partial y}{\partial \beta} &= E \sigma \left( \beta (p_1-p_2)x \right) \left\{ 1 - \sigma \left( \beta (p_1-p_2)x \right) \right\} (p_1-p_2)x \\
\cfrac{\partial y}{\partial p_1} &= E \sigma \left( \beta (p_1-p_2)x \right) \left\{ 2 - \sigma \left( \beta (p_1-p_2)x \right) \right\} \beta x \\
\cfrac{\partial y}{\partial p_2} &= Ex - E \sigma \left( \beta (p_1-p_2)x \right) \left\{ 2 - \sigma \left( \beta (p_1-p_2)x \right) \right\} \beta x
\end{align}
さて、実装はちょっと時間ないので今度やります...しばしお待ちください。
2020/10/21追記:実装してみました。ただしハイパーパラメータの学習は動作未確認のため多分動きません。
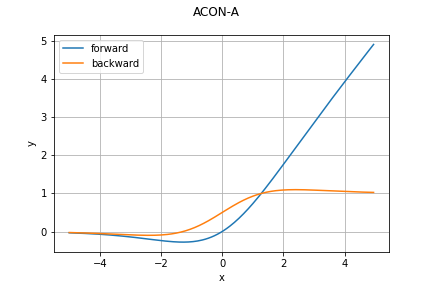
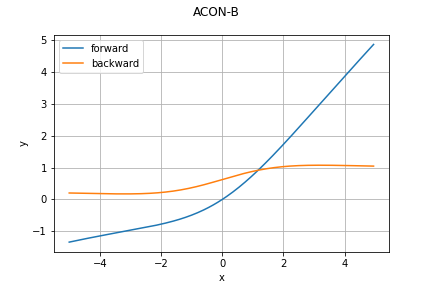
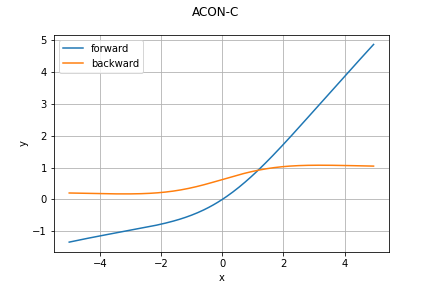
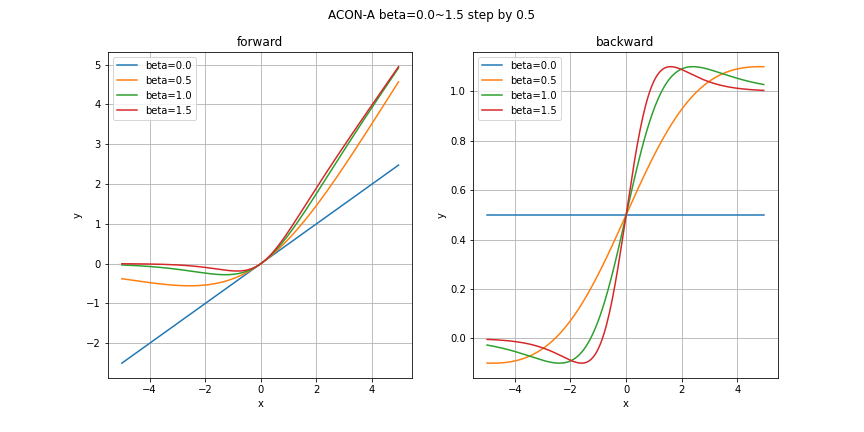
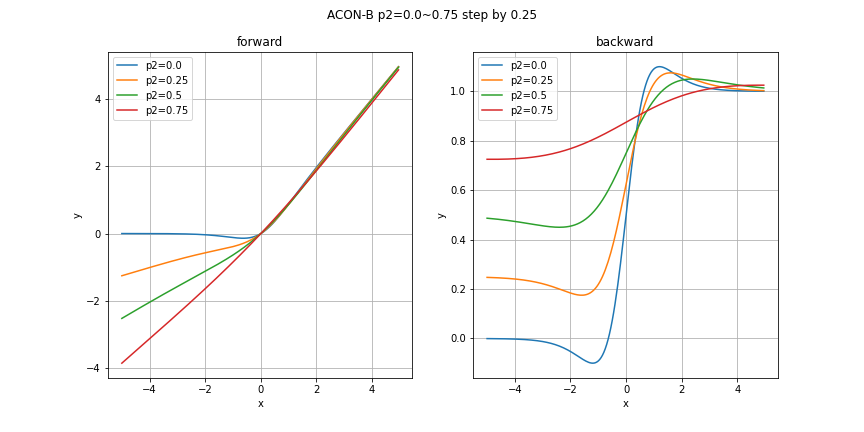
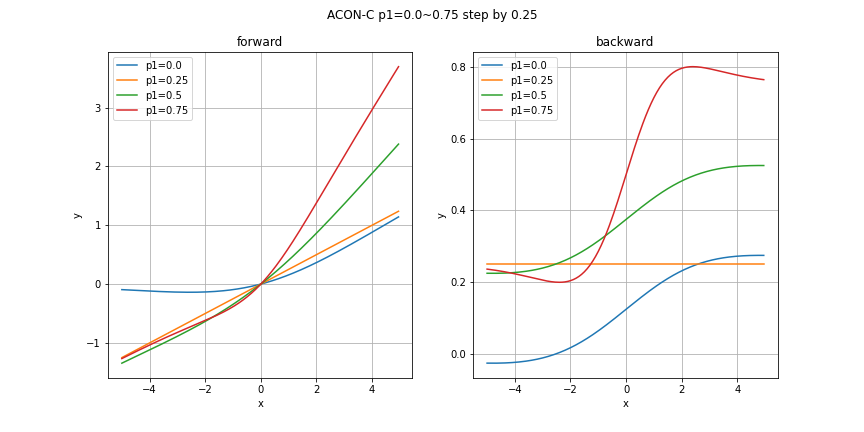
どのグラフも指定していないパラメータはデフォルト値を利用しています。今回の実装におけるデフォルト値は
\beta = 1.0, \quad p_1 = 1.0, \quad p_2 = 0.25
としています。
Mish関数
Mish関数はSwish関数よりもさらに最近の2019年に提案されたReLU関数の後継です。多くの場合でSwish関数よりも良い性能を発揮することが論文で示されています。(まだ論文をきちんと読んでませんがそう書いているそうです)
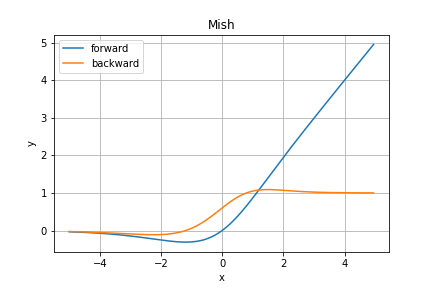
Swish関数と見た目ほぼ同じですが、ごくわずかに異なっています。
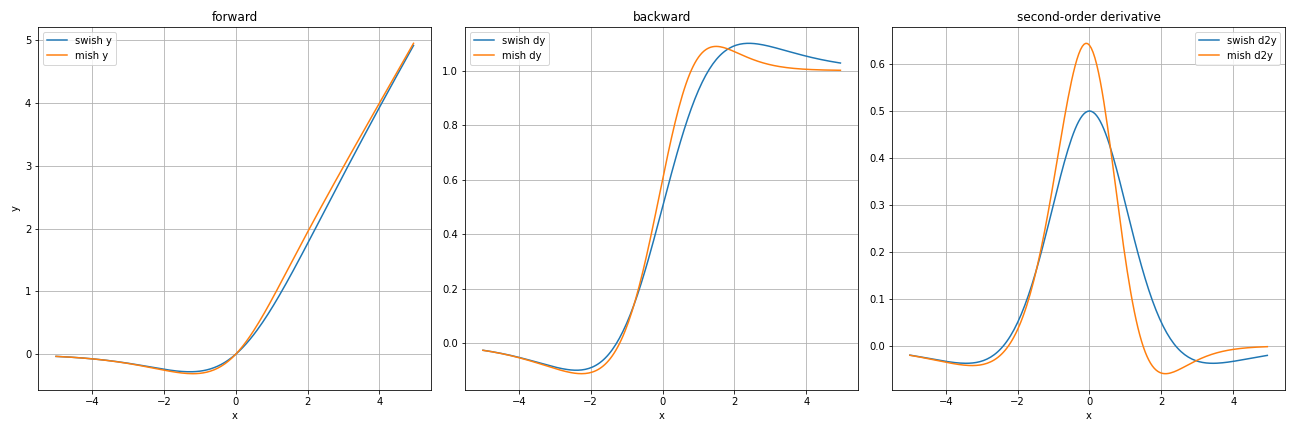
一番右のグラフが最も違いが表れていますね。このグラフはそれぞれの2回微分を計算したものです。
つまり、勾配の変化の度合いを表しているものです。
グラフから読み取れることとしては、特に$x=0$付近でMish関数の方がダイナミックに変化している$\Rightarrow$勾配計算においてより顕著に誤差が伝わる、ということです。
順伝播の数式としては
y = x \tanh{(\varsigma(x))} = x \tanh{(\ln{(1 + e^x)})}
となっており、逆伝播は少々複雑で
\cfrac{\partial y}{\partial x} = \cfrac{e^x \omega}{\delta^2}\\
\omega = 4(x + 1) + 4e^{2x} + e^{3x} + (4x + 6)e^x \\
\delta = 2e^x + e^{2x} + 2
のように計算されます。指数計算がたくさん登場するため計算負荷が高く、学習にReLU関数などより(ごく僅かですが)時間がかかってしまいます。
しかし精度の面でReLU関数を用いるよりも良い場合が多いため、学習時間と精度のトレードオフを加味して活性化関数を選択しましょう。
tanhExp関数
こちらは@reppy4620さんより情報をいただいたtanhExp関数です!
論文によると2020年3月のものですね〜凄まじく最近です。
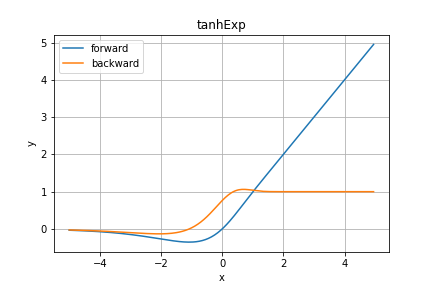
論文にある通り、ReLU関数の仲間ですね(ReLU familyと呼ぶみたい?)。
どうやらMNISTやCIFER-10、CIFER-100などの有名データセットにおいてMish関数をも超える性能を発揮してるっぽいです(まだちゃんと読んでません)。
Swish関数と比較してみると
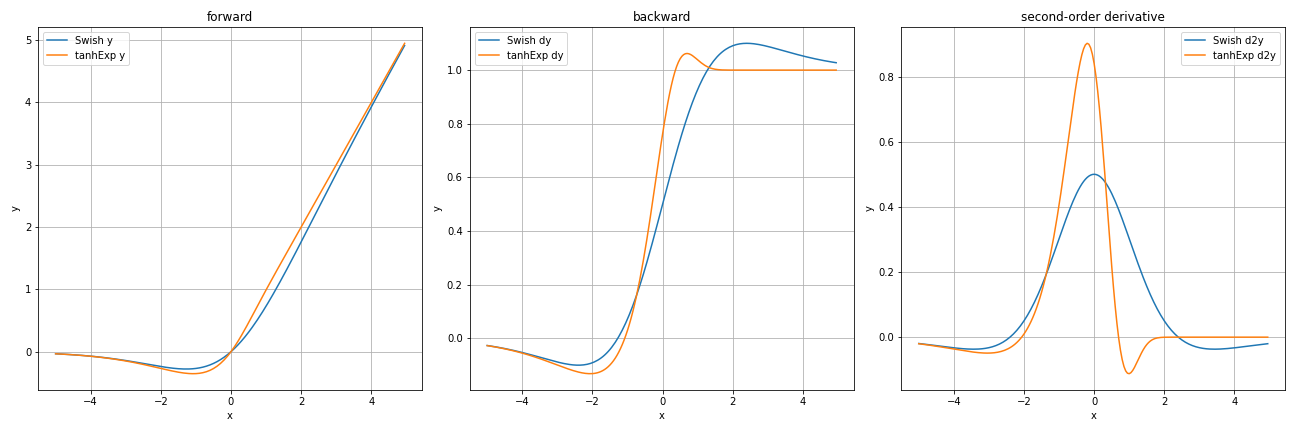
順伝播の出力はほぼ同じに見えますが、tanhExp関数の方が逆伝播においてより急勾配かつ微分値$1$を超える範囲が小さくなっていますね。勾配というのはすごくデリケートで、微分の絶対値が$1$より小さすぎるとすぐ勾配消失しますし、逆に$1$より大きすぎると勾配爆発という現象が起こります。その点でもtanhExp関数は優秀に見えますね。
続いてMish関数とも比較します。
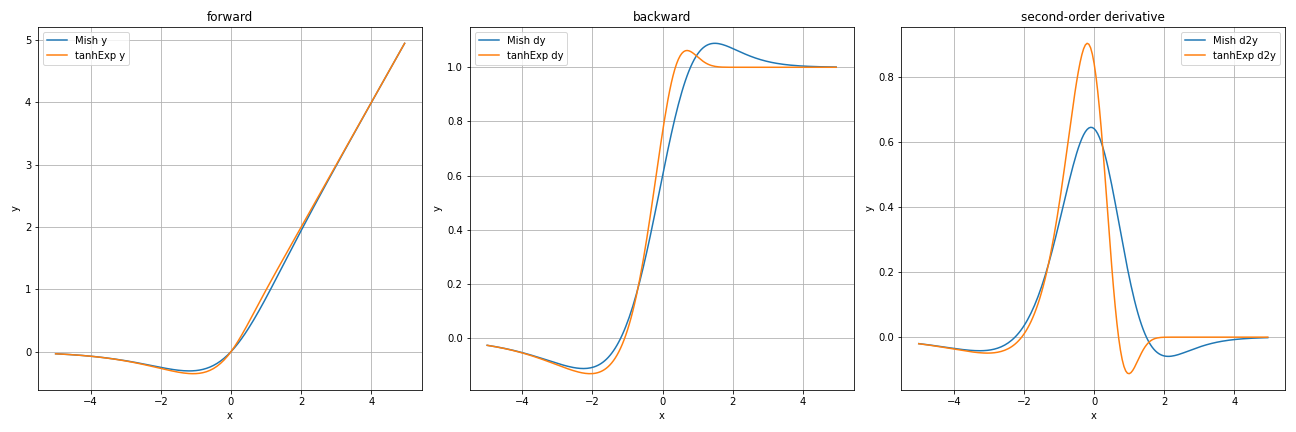
Mish関数はSwish関数よりかはtanhExp関数に追従してますね。しかしそれでもtanhExp関数の方が$0$付近での急勾配っぷりが優秀です。
では順伝播を数式で見てみましょう。
y = x \tanh(e^x)
Mish関数と同じくtanh関数を用いてますね。ここにきてtanh関数の注目度が高まっているんですかね〜
逆伝播は
\begin{align}
\cfrac{\partial y}{\partial x} &= \tanh(e^x) + xe^x\textrm{sech}^2(e^x) \\
&= \tanh(e^x) - xe^x(\tanh^2(e^x) - 1)
\end{align}
となります。Mish関数よりもずっとシンプルに計算できるのが良いですね〜
コード例
ここにはグラフを書く時に使用したコード例を載せておきます。実装する際の参考にでもしてください。
jupyter notebookを用いています。
activators.py
import numpy as np
class Activator():
def __init__(self, *args, **kwds):
pass
def forward(self, *args, **kwds):
raise NotImplemented
#raise Exception("Not Implemented")
def backward(self, *args, **kwds):
raise NotImplemented
#raise Exception("Not Implemented")
def update(self, *args, **kwds):
raise NotImplemented
#pass
class step(Activator):
def forward(self, x, *args, **kwds):
return np.where(x > 0, 1, 0)
def backward(self, x, *args, **kwds):
return np.zeros_like(x)
class identity(Activator):
def forward(self, x, *args, **kwds):
return x
def backward(self, x, *args, **kwds):
return np.ones_like(x)
class bentIdentity(Activator):
def forward(self, x, *args, **kwds):
return 0.5*(np.sqrt(x**2 + 1) - 1) + x
def backward(self, x, *args, **kwds):
return 0.5*x/np.sqrt(x**2 + 1) + 1
class hardShrink(Activator):
def __init__(self, lambda_=0.5, *args, **kwds):
self.lambda_ = lambda_
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where((-self.lambda_ <= x) & (x <= self.lambda_), 0, x)
def backward(self, x, *args, **kwds):
return np.where((-self.lambda_ <= x) & (x <= self.lambda_), 0, 1)
class softShrink(Activator):
def __init__(self, lambda_=0.5, *args, **kwds):
self.lambda_ = lambda_
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x < -self.lambda_, x + self.lambda_,
np.where(x > self.lambda_, x - self.lambda_, 0))
def backward(self, x, *args, **kwds):
return np.where((-self.lambda_ <= x) & (x <= self.lambda_), 0, 1)
class threshold(Activator):
def __init__(self, threshold, value, *args, **kwds):
self.threshold = threshold
self.value = value
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x > self.threshold, x, self.value)
def backward(self, x, *args, **kwds):
return np.where(x > self.threshold, 1, 0)
class sigmoid(Activator):
def forward(self, x, *args, **kwds):
return 1/(1 + np.exp(-x))
def backward(self, x, y, *args, **kwds):
return y*(1 - y)
class hardSigmoid(Activator):
def forward(self, x, *args, **kwds):
return np.clip(0.2*x + 0.5, 0, 1)
def backward(self, x, *args, **kwds):
return np.where((x > 2.5) | (x < -2.5), 0, 0.2)
class logSigmoid(Activator):
def forward(self, x, *args, **kwds):
return -np.log(1 + np.exp(-x))
def backward(self, x, *args, **kwds):
return 1/(1 + np.exp(x))
class act_tanh(Activator):
def forward(self, x, *args, **kwds):
return np.tanh(x)
def backward(self, x, *args, **kwds):
return 1 - np.tanh(x)**2
class hardtanh(Activator):
def forward(self, x, *args, **kwds):
return np.clip(x, -1, 1)
def backward(self, x, *args, **kwds):
return np.where((-1 <= x) & (x <= 1), 1, 0)
class tanhShrink(Activator):
def forward(self, x, *args, **kwds):
return x - np.tanh(x)
def backward(self, x, *args, **kwds):
return np.tanh(x)**2
class ReLU(Activator):
def forward(self, x, *args, **kwds):
return np.maximum(0, x)
def backward(self, x, *args, **kwds):
return np.where(x > 0, 1, 0)
class ReLU6(Activator):
def forward(self, x, *args, **kwds):
return np.clip(x, 0, 6)
def backward(self, x, *args, **kwds):
return np.where((0 < x) & (x < 6), 1, 0)
class leakyReLU(Activator):
def __init__(self, alpha=1e-2, *args, **kwds):
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.maximum(self.alpha * x, x)
def backward(self, x, *args, **kwds):
return np.where(x < 0, self.alpha, 1)
class ELU(Activator):
def __init__(self, alpha=1., *args, **kwds):
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x >= 0, x, self.alpha*(np.exp(x) - 1))
def backward(self, x, *args, **kwds):
return np.where(x >= 0, 1, self.alpha*np.exp(x))
class SELU(Activator):
def __init__(self, lambda_=1.0507, alpha=1.67326, *args, **kwds):
self.lambda_ = lambda_
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x >= 0, self.lambda_*x,
self.lambda_*self.alpha*(np.exp(x)-1))
def backward(self, x, *args, **kwds):
return np.where(x >= 0, self.lambda_, self.lambda_*self.alpha*np.exp(x))
class CELU(Activator):
def __init__(self, alpha=1., *args, **kwds):
self.alpha = alpha
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return np.where(x >= 0, x, self.alpha*(np.exp(x/self.alpha)-1))
def backward(self, x, *args, **kwds):
return np.where(x >= 0, 1, np.exp(x/self.alpha))
class softmax(Activator):
def forward(self, x, *args, **kwds):
exp_x = np.exp(x-np.max(x, axis=1, keepdims=True))
return exp_x/np.sum(exp_x, axis=1, keepdims=True)
def backward(self, x, y, *args, **kwds):
return y*(1 - y)
class softmin(Activator):
def forward(self, x, *args, **kwds):
exp_mx = np.exp(-x)
return exp_mx/np.sum(exp_mx, axis=1, keepdims=True)
def backward(self, x, y, *args, **kwds):
return -y*(1 - y)
class logSoftmax(Activator):
def forward(self, x, *args, **kwds):
exp_x = np.exp(x)
return np.log(exp_x/np.sum(exp_x, axis=1, keepdims=True))
def backward(self, x, y, *args, **kwds):
return 1 - np.exp(y)
class softplus(Activator):
def forward(self, x, *args, **kwds):
return np.logaddexp(x, 0)
def backward(self, x, *args, **kwds):
return 1/(1 + np.exp(-x))
class softsign(Activator):
def forward(self, x, *args, **kwds):
return x/(1 + np.abs(x))
def backward(self, x, *args, **kwds):
return 1/(1 + np.abs(x))**2
class Swish(Activator):
def __init__(self, beta=1, *args, **kwds):
self.beta = beta
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
return x/(1 + np.exp(-self.beta*x))
def backward(self, x, y, *args, **kwds):
return self.beta*y + (1 - self.beta*y)/(1 + np.exp(-self.beta*x))
def d2y(self, x, *args, **kwds):
return (-0.25*self.beta*(self.beta*x*np.tanh(0.5*self.beta*x) - 2)
*(1 - np.tanh(0.5*self.beta*x)**2))
class hardSwish(Activator):
def forward(self, x, *args, **kwds):
return x*np.clip(x+3, 0, 6)/6
def backward(self, x, *args,**kwds):
return np.where((-3 < x) & (x < 3), (2*x + 3)/6, np.clip(x, 0, 1))
class ACON(Activator):
def __init__(self, acon_type, *args, p1=1, p2=0.25, beta=1,
opt="adam", **kwds):
if acon_type == "acona":
self.p1 = p1
self.p2 = 0
self.acon_type = "acona"
elif acon_type == "aconb":
self.p1 = p1
self.p2 = p2
self.acon_type = "aconb"
elif acon_type == "aconc":
self.p1 = p1
self.p2 = p2
self.acon_type = "aconc"
else:
raise KeyError("Unknown ACON type: <{}>.".format(acon_type))
if acon_type in ["aconb", "aconc"]:
#self.opt = get_opt(opt, *args, **kwds)
pass
# ベータの設定
switch_args = []
self.beta = None
class BaseSwitch():
def forward(self, x):
pass
def backward(self, grad):
pass
def update(self, *args, **kwds):
pass
if isinstance(beta, str):
if "pixel" in beta:
class Beta(BaseSwitch):
def forward(self, x):
self.value = 1/(1+np.exp(-x))
elif "channel" in beta:
if "n_channel" in kwds:
C = kwds["n_channel"]
else:
raise KeyError("I must need 'n_channel' value to use channel-wise switch.")
if "r" in kwds:
r = kwds["r"]
else:
r = 16
class Beta(BaseSwitch):
def __init__(self, C, r, opt, **kwds):
self.C = C
self.r = r
self.w1 = np.random.randn((C, C//r))
self.w2 = np.random.randn((C//r, C))
self.opt = get_opt(opt, **kwds)
def forward(self, x):
self.sumx = np.sum(x, axis=(2, 3))
self.first = self.sumx@self.w1
self.value = 1/(1+np.exp(-self.first@self.w2))
def backward(self, grad):
self.grad_w2 = self.first.T@(grad * self.value*(1-self.value))
self.grad_w1 = self.sumx.T@((grad * self.value*(1-self.value))@self.w2.T)
def update(self, *args, **kwds):
dw1, dw2 = self.opt.update(self.grad_w1, self.grad_w2, *args, **kwds)
self.w1 -= dw1
self.w2 -= dw2
switch_args.append(C)
switch_args.append(r)
switch_args.append(opt)
switch_args.append(kwds)
elif "layer" in kwds:
class Beta(BaseSwitch):
def forward(self, x):
self.value = 1/(1+np.exp(-np.sum(x, axis=(1, 2, 3))))
else:
raise KeyError("Unknown switch type: <{}>.".format(beta))
else:
if isinstance(beta, int) or isinstance(beta, float):
class Beta(BaseSwitch):
def __init__(self, value):
self.value = value
switch_args.append(beta)
else:
if not (hasattr(beta, "forward") and hasattr(beta, "backward") and hasattr(beta, "update")):
raise KeyError("Using designed function, the type of switch 'beta' must be a <class>"
+ " and have method 'forward' and 'backward' and 'update'.")
self.beta = beta
if self.beta is None:
self.beta = Beta(*switch_args)
def forward(self, x, *args, **kwds):
self.beta.forward(x)
self.sigmoid_value = 1/(1+np.exp(-self.beta.value*(self.p1-self.p2)*x))
return (self.p1-self.p2)*x*self.sigmoid_value + self.p2*x
def backward(self, x, grad, *args, **kwds):
if self.acon_type in ["aconb", "aconc"]:
self.grad_p1 = np.sum(grad*self.sigmoid_value*(2-self.sigmoid_value)*self.beta.value*x)
self.grad_p2 = np.sum(grad*x - grad*self.sigmoid_value*(2-self.sigmoid_value)*self.beta.value*x)
self.beta.backward(grad)
return (((self.p1-self.p2)*(1+np.exp(-self.beta.value*(self.p1-self.p2)*x))
+ self.beta.value*(self.p1-self.p2)**2*np.exp(-self.beta.value*(self.p1-self.p2)*x)*x)
/(1+np.exp(-self.beta.value*(self.p1-self.p2)*x))**2
+ self.p2)
def update(self, *args, **kwds):
if self.acon_type in ["aconb", "aconc"]:
dp1, dp2 = self.opt.update(self.grad_p1, self.grad_p2, *args, **kwds)
if self.acon_type in ["aconc"]:
self.p1 -= dp1
self.p2 -= dp2
self.beta.update(*args, **kwds)
class Mish(Activator):
def forward(self, x, *args, **kwds):
return x*np.tanh(np.logaddexp(x, 0))
def backward(self, x, *args, **kwds):
omega = (4*(x + 1) + 4*np.exp(2*x)
+ np.exp(3*x) + (4*x + 6)*np.exp(x))
delta = 2*np.exp(x) + np.exp(2*x) + 2
return np.exp(x)*omega/delta**2
def d2y(self, x, *args, **kwds):
omega = (2*(x + 2)
+ np.exp(x)*(np.exp(x)*(-2*np.exp(x)*(x - 1) - 3*x + 6)
+ 2*(x + 4)))
delta = np.exp(x)*(np.exp(x) + 2) + 2
return 4*np.exp(x)*omega/delta**3
class tanhExp(Activator):
def forward(self, x, *args, **kwds):
return x*np.tanh(np.exp(x))
def backward(self, x, *args, **kwds):
tanh_exp_x = np.tanh(np.exp(x))
return tanh_exp_x - x*np.exp(x)*(tanh_exp_x**2 - 1)
def d2y(self, x, *args, **kwds):
tanh_exp = np.tanh(np.exp(x))
return (np.exp(x)*(-x + 2*np.exp(x)*x*tanh_exp - 2)
*(tanh_exp**2 - 1))
class maxout(Activator):
def __init__(self, n_prev, n, k, wb_width=5e-2, *args, **kwds):
self.n_prev = n_prev
self.n = n
self.k = k
self.w = wb_width*np.random.rand((n_prev, n*k))
self.b = wb_width*np.random.rand(n*k)
super().__init__(*args, **kwds)
def forward(self, x, *args, **kwds):
self.x = x.copy()
self.z = np.dot(self.w.T, x) + self.b
self.z = self.z.reshape(self.n, self.k)
self.y = np.max(self.z, axis=1)
return self.y
def backward(self, g, *args, **kwds):
self.dw = np.sum(np.dot(self.w, self.x))
test_activators.py
import string
import numpy as np
import matplotlib.pyplot as plt
_act_dic = {"step": step,
"identity": identity,
"bentidentity": bentIdentity,
"hardshrink": hardShrink,
"softshrink": softShrink,
"threshold": threshold,
"sigmoid": sigmoid,
"hardsigmoid": hardSigmoid,
"logsigmoid": logSigmoid,
"tanh": act_tanh,
"tanhshrink": tanhShrink,
"hardtanh":hardtanh,
"relu": ReLU,
"relu6": ReLU6,
"leakyrelu": leakyReLU, "lrelu": leakyReLU,
"elu": ELU,
"selu": SELU,
"celu": CELU,
"softmax": softmax,
"softmin": softmin,
"logsoftmax": logSoftmax,
"softplus": softplus,
"softsign": softsign,
"swish": Swish,
"hardswish": hardSwish,
"acona": ACON, "aconb": ACON, "aconc": ACON,
"mish": Mish,
"tanhexp": tanhExp,
}
def get_act(name, *args, **kwds):
name = name.lower().translate(str.maketrans('', '',string.punctuation))
if name in _act_dic.keys():
if "acon" in name:
activator = _act_dic[name](name, *args, **kwds)
else:
activator = _act_dic[name](*args, **kwds)
else:
raise ValueError(name + ": Unknown activator")
return activator
def plot_graph(x, name, *args, **kwds):
activator = get_act(name, *args, **kwds)
y = activator.forward(x, *args, **kwds)
dx = activator.backward(x, y, *args, **kwds)
fig, ax = plt.subplots(1)
ax.plot(x[0], y[0], label="forward")
ax.plot(x[0], dx[0], label="backward")
fig.suptitle(name)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.grid()
ax.legend(loc="best")
fig.savefig("{}.png".format(name))
#fig.show()
#plt.close(fig)
def vs_plot(x, A, B):
A_activator = get_act(A)
B_activator = get_act(B)
y_A = {}
y_B = {}
y_A["{} y".format(A)] = A_activator.forward(x)
y_B["{} y".format(B)] = B_activator.forward(x)
y_A["{} dy".format(A)] = A_activator.backward(x,
y_A["{} y".format(A)])
y_B["{} dy".format(B)] = B_activator.backward(x,
y_B["{} y".format(B)])
y_A["{} d2y".format(A)] = A_activator.d2y(x, y_A["{} y".format(A)])
y_B["{} d2y".format(B)] = B_activator.d2y(x, y_B["{} y".format(B)])
fig, ax = plt.subplots(1, 3, figsize=(18, 6))
for i, key in enumerate(y_A):
ax[i].plot(x[0], y_A[key][0], label=key)
ax[i].set_xlabel("x")
ax[i].set_ylabel("y")
ax[i].grid()
for i, key in enumerate(y_B):
ax[i].plot(x[0], y_B[key][0], label=key)
ax[i].legend(loc="best")
ax[0].set_title("forward")
ax[1].set_title("backward")
ax[2].set_title("second-order derivative")
fig.tight_layout()
fig.savefig("{}_vs_{}.png".format(A, B))
plt.show()
def param_plot(x, name, param_dic, *args, **kwds):
for param in param_dic:
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
for i in param_dic[param]:
kwds[param] = i
activator = get_act(name, *args, **kwds)
y = activator.forward(x, *args, **kwds)
dx = activator.backward(x, y, *args, **kwds)
ax[0].plot(x[0], y[0], label="{}={}".format(param, np.round(i, 2)))
ax[1].plot(x[0], dx[0], label="{}={}".format(param, np.round(i, 2)))
fig.suptitle(name+" {}={}~{} step by {}".format(param,
np.round(param_dic[param][0], 2),
np.round(param_dic[param][-1], 2),
np.round(param_dic[param][1]-param_dic[param][0], 2)))
ax[0].set_title("forward")
ax[1].set_title("backward")
ax[0].set_xlabel("x")
ax[0].set_ylabel("y")
ax[1].set_xlabel("x")
ax[1].set_ylabel("y")
ax[0].grid()
ax[1].grid()
ax[0].legend(loc="best")
ax[1].legend(loc="best")
fig.savefig("{}.png".format("_".join([name, param,
str(np.round(param_dic[param][0], 2)),
str(np.round(param_dic[param][-1], 2)),
str(np.round(param_dic[param][1]-param_dic[param][0], 2))])))
x = np.arange(-5, 5, 5e-2).reshape(1, -1)
plot_graph(x, "step")
plot_graph(x, "identity")
plot_graph(x, "bent-identity")
plot_graph(x, "hard-shrink")
plot_graph(x, "soft-shrink")
plot_graph(x, "threshold", -1, -2)
plot_graph(x, "sigmoid")
plot_graph(x, "hard-sigmoid")
plot_graph(x, "log-sigmoid")
plot_graph(x, "tanh")
plot_graph(x, "tanh-shrink")
plot_graph(x, "hard-tanh")
plot_graph(x, "ReLU")
plot_graph(x + 2, "ReLU6")
plot_graph(x, "leaky-ReLU")
plot_graph(x, "ELU")
plot_graph(x, "SELU")
plot_graph(x, "CELU")
plot_graph(x, "softmax")
plot_graph(x, "softmin")
plot_graph(x, "log-softmax")
plot_graph(x, "softplus")
plot_graph(x, "softsign")
plot_graph(x, "Swish")
plot_graph(x, "hard-swish")
plot_graph(x, "ACON-A")
plot_graph(x, "ACON-B")
plot_graph(x, "ACON-C")
plot_graph(x, "Mish")
plot_graph(x, "tanhExp")
vs_plot(x, "Swish", "hard-swish")
vs_plot(x, "Swish", "Mish")
vs_plot(x, "Swish", "tanhExp")
vs_plot(x, "Mish", "tanhExp")
param_plot(x, "ACON-A", {"beta": np.arange(0, 2, 0.5)})
param_plot(x, "ACON-B", {"p2": np.arange(0, 1, 0.25)}, beta=2)
param_plot(x, "ACON-C", {"p1": np.arange(0, 1, 0.25)}, beta=2)
他にも実装中のものもいくつかあります。そのうち追加すると思います...
参考
- 【人工知能】活性化関数の種類と違い。メリットデメリット。
- Bent Identity Activation Function
- Kerasのhard_sigmoidが max(0, min(1, (0.2 * x) + 0.5)) である話
- Swish活性化関数の紹介
- ついに誕生!期待の新しい活性化関数「Mish」解説
- 活性化関数業界の期待のルーキー”Mish”について
- Pytorch
- Global Average Pooling(GAP)を理解してみる
追記リスト&謝辞
- @reppy4620さんよりtanhExp関数の情報をいただきました!ご丁寧に論文のリンクまで載せてくださり誠にありがとうございました!
- @tsubota-kougaさんよりhardSwish関数の情報をいただきました!論文の検証サイトですかね?必要な情報を見やすく載せてあるサイトのリンクを載せてくださり誠にありがとうございました!
- 再び@tsubota-kougaさんより、ACON関数の情報をいただきました!コメントに綺麗に纏まっていますのでそちらも是非ご参照ください!いつもありがとうございます!