はじめに
グローバーアルゴリズム(6量子ビット)をblueqatで実装しましたという話でもなければ、数理を解説したという記事でもない。勿論、実装の話は含むが、この記事は 「均一重ね合わせではない場合」 でグローバーを試してみたらどうなるの?というものである。
タイトルに第7回とあるように、そもそも全8回の「【数式なしの量子コンピュータ】新視点セルオートマトンとグローバー」と題した連載の7回目の記事のつもりだったのだが。コロナ禍の巣籠のGWに1回目の投稿を出したので、夏休みまでで終えるつもりが・・・こんな季節になってしまって。それで Advent Calendar で投稿してみることとした。
7-1. 目的
グローバーアルゴリズム
グローバーアルゴリズムは、よく「データベースの探索」の量子アルゴリズムと言われている。グローバーさんの論文にも、「整列化されていないアドレス帳から、知り合いの携帯番号を探すのに使われる」と記載されているらしい。ググればWikipediaをはじめ多くの検索結果が出てくる。その中でQiita記事として検索されたもの14件。以下にそれらのリンクを記した。
・量子アルゴリズムの基本:Groverのアルゴリズムの確認 ・・・ @SamN
・Grover アルゴリズムについて ・・・ @kyamaz
・グローバーアルゴリズム (Grover's algorithm) ・・・@KeiichiroHiga
・Quantum Katas で始める量子コンピュータ入門 |10⟩: Grover's algorithm ・・・ @tehishik
・Grover(グローバー)のアルゴリズム ・・・@YuichiroMinato
・Cirq で Grover アルゴリズム を実装 ・・・ @ymurata
・blueqatで4qubitのGloverのアルゴリズム ・・・ @mi2valley
・Groverアルゴリズムで実際にデータを検索(!?) ・・・ @shimo3san
・グローバーのアルゴリズムの量子回路を組む ・・・ @shiibass
・blueqatでグローバーアルゴリズム ・・・ @KeiichiroHiga
・グローバーのアルゴリズムの一般化 Quantum Amplitude Amplification の論文解説 ・・・ @koke-saka
・Groverアルゴリズムで15を因数分解 ・・・ @shimo3san
・Qiskit素人がIBM Quantum Challenge 2019で準優勝するまで ・・・@quaeva
・Quantum Katas で始める量子コンピュータ入門 |12⟩: Solve SAT with Grover ・・・ @tehishik
少しだけ
グローバーアルゴリズムを表現すれば、1と0が重ね合わさったn個の量子ビットの中から、ある特定のn個並んだ1と0の組み(状態ベクトルと表現)の確率振幅(=二乗すると確率)のみ、他の組み合わせの確率振幅より高くすること。そのアルゴリズムとしては、まず、増幅させたいある特定の状態ベクトルにマーキングをする。マーキングは位相を反転(つまり確率振幅の符号を反転)させる。その後、その状態ベクトルの確率振幅のみをある手順で増幅させるというものだ。数理的に詳しく知りたい方は、上述したQiita記事のリンクの内、上4つを参照されたし。増幅が足りなければ、再度マーキングし増幅する手順を繰り返す。ただ、確率振幅の最大値を超えても繰り返しを続けると確率振幅は減少に転ずる。もっと続けると再び増加に・・・グローバーアルゴリズムでの確率振幅は繰り返し回数でのサイン波となっている。その周期や位相そして振幅は?・・・次々章で!
例えば、n=6つまり6量子ビットを考えた時、状態ベクトルは、|000000> から|111111>まで、$2^6=64$個ある。そして、この量子状態 $ψ$ は、これら64個の状態ベクトルとそれぞれの確率振幅$a_i$の線形結合として次式で表現されている。
$$ψ=a_1|000000>+a_2|000001>+…+a_{36}|100011>+…+a_{63}|011111>+a_{64}|111111>(式1)$$
ここでi番目の状態ベクトルの確率振幅 $a_i$ の二乗 $a_i^2$ はi番目の状態ベクトルの確率で、64個の状態ベクトルの確率の和は当然、$\sum a_i^2$=1となっている。ここで、例えば、|100011>を増幅する目的でグローバーアルゴリズムを適用するとすれば、マーキングとして$+a_{36}$の符号を反転させ増幅器を通す。実行後の確率振幅を$b_{36}$とすれば、増加のフェーズでは、$b_{36}^2 > a_{36}^2$ となっている。この操作を繰り返せば、次第に|100011>の確率だけが高くなり他のベクトルの確率は小さくなる。さらに続けていくと減少フェーズになり、$b_{36}^2 < a_{36}^2$ となる。
ここでの目的
ところで、多くの解説や記事の場合、初期の全ての状態ベクトルの確率振幅は暗黙のうちに等しいことになっている。つまり確率も等しく、n量子ビットなら確率は$1/2^n$である。$$a_1^2=...=a_i^2=...=a_n^2=1/2^n ⇒ a_i=±1/\sqrt{2^n}$$
全ての状態ベクトルの確率振幅が等しいので $a_i$ の符号もプラスかマイナスかの一方で統一されている。これを均一重ね合わせと言う。この状態は単一の量子ビットで見た時、観測を繰り返した場合に1又は0が半々の割合で出現することを意味している。ある意味では理想的な状態で、現実世界ではなかなかあり得ない・・・が量子力学的には?
多くのグローバーアルゴリズムの実装例では、まず前述の均一重ね合わせ状態を作るために、最初にゼロである全ての量子ビットをアダマールゲート(h[:])に通す。結果、確率振幅は $a_i=1/\sqrt{2^n}$ に均一化される。もし、この操作をする前に量子ゲートが存在していたら。例えば、1番目の量子ビットだけをフリップ (x[0])させた後、アダマールゲートを通すと、一部の確率振幅にマイナスが出現するだろう。すると、たちまちマーキングできずオーソドックスなグローバーはできなくなってしまう。さらに量子ビット毎に1,0の重ね合わせが半々とは異なる割合となっていたら、つまり均一重ね合わせではない場合では? それにグローバーアルゴリズムを適用すると何が生じるのだろう? それを国産の量子コンピュータSDKであるblueqatで6量子ビットのグローバーアルゴリズムを実装し確かめてみる。それがここでの目的である。
7-2. 方法
手順をpythonでのモジュールを基に以下①から⑥で述べる。丸数字の後ろの小見出しの後ろがモジュール名である。尚、これらのモジュールはGithubのリポジトリ名 q-cams で公開中。使い方は2回目の「2-1.q-camの構造とモジュール」に記載しているので使いたい方はそちらを参照されたし。
①確率的初期状態のセット qcam.propinit
グローバーアルゴリズムを適用する6個の各量子ビットに1が出る出現確率をセットする。(i番目の量子ビットのセットした確率を $P_i$ とする)。この部分が、前述した通り多くの解説や実装例のような均一重ね合わせでは、アダマールでセットするため必ず $P_0=P_1=P_2=P_3=P_4=P_5=1/2$ となっている。しかし、ここでは、$0≦P_i≦1$ であれば、お隣の量子ビットの P と異なっていようが、等しかろうが問題ではない。ここで、この6量子ビットの確率のセットを確率的初期状態と称することとしよう。表現としては$(P_0,P_1,P_2,P_3,P_4,P_5)$とする。各量子ビットへのこの確率のセットは、セットする量子ビットiのY軸回転ゲートで$P_i$から計算した回転角θ分回転させることでできる。あるいはX軸回転ゲートを用いても同様である。回転角θは $\ θ=2arcsin ( \sqrt{P_i}\ ) $ である。尚、$\ P_i=1/2$ の時 θ=π/2=90度 であり、これはアダマールゲートそのものとなる。また、U3ゲートを用いても確率のセットをすることができる。この確率的初期状態のセットに関しては、2回目の「2-2. 1,0ではない確率的初期状態(ry 又は rx 又は u3 ゲートで作る)」で詳述しているので知りたい方は参照されたし。
確率的初期状態セットのコード
def propinit(NN, c, ppinit_a):
for i in range(NN):
theta=2* np.arcsin(np.sqrt(ppinit_a[i])) # Correlation between Probability and Rotation Angle
c.ry(theta)[i] # You can change from ry to rx.
return
NNは量子ビット数、CはBlueqatのサーキットオブジェクト、ppinit_aは配列、$[P_0,P_1,P_2,P_3,P_4,P_5]$、npはnumpy。
蛇足ながら、これらの量子ビットを一次元に並んだセルに見立ててみる。セルの中にある玉あるいは車がセルに存在する時1、空の時0。これをあるルールに従って1を動かせばセルオートマトンとなる。あるセルとその両隣を含めたセルの状態だけで決定する単純なルールは256種類あり、ウルフラムコードと称し1から256番までの番号をルールに付して呼ぶ。このようなルールに従い動かすことを遷移と言い、一度遷移させたことを一単位時間経過したと言う。この遷移を繰り返せば、次々と1と0の並びの様が変化していく。これを時間発展と言う。その発展の有り様はルールによって異なりウルフラムクラスと言う4パターンに分類される。ところで、玉あるいは車が、あるセルに存在(確率1)、空(確率0)、でもない確率、例えば0.3で存在しますとは?詳しくは4回目を参照されたし。
②マルチ制御NOTゲートの準備 qmcn.ccccccx
マーキング部も増幅部もマルチ制御NOTゲートが必要となる。そこでまずは少しだけ、マルチ制御NOTゲートの作成方法を述べる。詳しくは3回目の「簡単に作成できるマルチ制御ゲート」を参照されたし。n=6であれば 5制御ビット、1標的ビットの ccccccxゲートが必要になる。が、残念ながらblueqatの標準のゲートとしては制御ビットが3以上のマルチ制御NOTゲートは準備されていない。そのためn量子ビットのマルチ制御NOTを構成するのに、$2^n−2$ 個の制御NOTゲートと $2^n−1$ 個の制御Z軸回転ゲート(位相回転ゲート)及び一対のアダマールゲートを用い自製することになる。これらを構成するにあたってはグレーコードと言うものが役に立つが、その利用方法はここでは記載しないので、3回目を!ただ、pythonのモジュールとして記述したblueqatのコードが整然とできたので以下にコードを載せた。
ccccccxゲート(モジュール)のコード
def ccccccx(c,c0,c1,c2,c3,c4,c5,ta):
ang=np.pi/32
c.h[ta] #Hadamard
c.crz(ang)[c0,ta] #Gray code 1
c.cx[c0,c1].crz(-ang)[c1,ta].cx[c0,c1].crz(ang)[c1,ta] #Gray code 11 & 1
c.cx[c1,c2].crz(-ang)[c2,ta].cx[c0,c2].crz(ang)[c2,ta] #Gray code 110 & 111
c.cx[c1,c2].crz(-ang)[c2,ta].cx[c0,c2].crz(ang)[c2,ta] #Gray code 101 & 100
c.cx[c2,c3].crz(-ang)[c3,ta].cx[c0,c3].crz(ang)[c3,ta] #Gray code 1100 & 1101
c.cx[c1,c3].crz(-ang)[c3,ta].cx[c0,c3].crz(ang)[c3,ta] #Gray code 1111 & 1110
c.cx[c2,c3].crz(-ang)[c3,ta].cx[c0,c3].crz(ang)[c3,ta] #Gray code 1010 & 1011
c.cx[c1,c3].crz(-ang)[c3,ta].cx[c0,c3].crz(ang)[c3,ta] #Gray code 1000 & 1000
c.cx[c3,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 11000 & 11001
c.cx[c1,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 11011 & 11010
c.cx[c2,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 11110 & 11111
c.cx[c1,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 11101 & 11100
c.cx[c3,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 10101 & 10111
c.cx[c1,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 10110 & 10010
c.cx[c2,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 10010 & 10011
c.cx[c1,c4].crz(-ang)[c4,ta].cx[c0,c4].crz(ang)[c4,ta] #Gray code 10001 & 10000
c.cx[c4,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 110000 & 110001
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 110011 & 110010
c.cx[c2,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 110110 & 110111
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 110101 & 110100
c.cx[c3,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 111100 & 111101
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 111111 & 111110
c.cx[c2,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 111010 & 111011
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 111001 & 111000
c.cx[c4,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 101000 & 101001
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 101011 & 101010
c.cx[c2,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 101110 & 101111
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 101101 & 101100
c.cx[c3,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 100100 & 100101
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 100111 & 100110
c.cx[c2,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 100010 & 100011
c.cx[c1,c5].crz(-ang)[c5,ta].cx[c0,c5].crz(ang)[c5,ta] #Gray Code 100001 & 100000
c.h[ta] #Hadamard
return
③グローバーアルゴリズムの実装 qproc
さて、ようやく準備がととのったのでグローバーアルゴリズムの本体に入る。
●マーキング
まずはマーキングである。最初に最も単純にマーキングできる、|111111> に対して行うことを考える。|111111> のマーキング方法はと言うと、式1の最終項、つまり|111111> の確率振幅 $a_{64}$ の符号を反転させる操作を行うことである。方法論を言葉で言うと、第1量子ビットから第5量子ビットまでが全て1である時に、第6量子ビット目の位相を反転させると $a_{64}$の符号は入れ替わる。つまり第1から第5を制御ビットとし、第6を標的ビットにしたマルチ制御位相反転ゲート=マルチ制御Zゲートを行うことである。しかし、先ほどのマルチ制御NOTゲートと同様で、残念なことにblueqatの標準のゲートとしてはマルチ制御Zゲートは準備されていない。が、ご安心を。アダマール演算によるパウリ演算の変換 $Z=HXH$ が使える。従って、
ccccccz[0,1,2,3,4,5]=h[5].ccccccx[0,1,2,3,4,5].h[5]
以上で確率振幅 $a_{64}$ の符号のみがマイナスとなる。では、$+a_{36}$の符号、つまり|100011>を反転させるには? 状態ベクトル|111111> と比較すると状態ベクトルの左から2,3,4つ目がフリップしている・・・と言うことは・・・2,3,4つ目に相当する第4,3,2量子ビット(第0量子ビットが左に注意)をフリップさせればよいのでは? 実はその通りで以下で$+a_{36}$のみの符号を反転させられる。ちなみに、最後にフリップを戻すのを忘れないように。
x[2,3,4].h[5].ccccccx[0,1,2,3,4,5].h[5].x[2,3,4] 他の状態ベクトルでも全て同様にできる。
●振幅増幅
次は、振幅増幅である。こちらもマーキングと似ている。数理的な解説は再び上述したQiita記事のリンクの内の一番上あたりを参照されたし。式2を全アダマール演算h[:]と全フリップ演算x[:]で対称にサンドイッチさせると実施できる。つまり
h[:].x[:].h[5].ccccccx[0,1,2,3,4,5].h[5].x[:].h[:]
●コード
以下の折りたたみに|100011>をマーキングする場合のコードを示した。別の状態ベクトルをマーキングするにはプログラム中に # qubit in x gate depends on vector you want to markとコメントした行のxゲートを上述した方法で書き換えればよい。
グローバーアルゴリズム部分(qproc)コード
def qproc():
c.x[2,3,4].h[N-1] # qubit in x gate depends on vector you want to mark
qmcn.cccccx(c,0,1,2,3,4,5)
c.h[N-1].x[2,3,4] # qubit in x gate depends on vector you want to mark
c.h[:].x[:].h[N-1] # amplifier
qmcn.cccccx(c,0,1,2,3,4,5)
c.h[N-1].x[:].h[:]
return
④制御プログラム(本体) q-camgrax.py qcam.qvextract
①で各量子ビットにセットする$(P_0,P_1,P_2,P_3,P_4,P_5)$の値そのものは、コンソールから入力するのではなく、プログラムの初期設定として、例えば、$(0.4,0.6,0.3,0.7,0.2,0.8)$であれば、initial_a=np.array([0.4,0.6,0.3,0.7,0.2,0.8],dtype='float')と与える。この確率的初期状態を ③のグローバーアルゴリズムに適用する。その手順としては、はじめに、グローバーを適用する繰り返し回数としてpstepという変数を使うこととする。③のグローバーアルゴリズム本体であるqprocをpsetp回数分ループさせる。当然、pstepの最初は 1で、その時qprocは1回だけ呼び出される。ループ後、blueqatのコードとしてのrunを行う。ただしここでは、観測をせずにblueqatの状態ベクトルごとの確率振幅(複素数)のリストから、モジュールqcam.qvextractを用いて結果を得る。その方法は2回目の「2-3. blueqatの状態ベクトル表示からのベクトルと確率の抽出」で詳述しているので知りたい方はそちらを参照されたし。得られた結果は後述するがコンソールに出力する。ここまでを1ステップあるいは1単位時間経過と言う。さらにその後、pstepをインクリメントし次ステップに移る。すると次はqprocは2回連続呼び出され、その後runし結果だ出す。再びpstepを 1インクリメントする。このステップを好きなだけ繰り返せばよい。全体の繰り返しはwhileで組んでおり 'y' 以外のインプットでエスケープできる。エスケープ後、ファイナライズとして後述する、纏め結果出力とプロットを実行し終了。この制御構造自体も2回目の「2-1. q-camの構造とモジュール」で詳述している。尚、以下のコード例はマーキングとして|100011>を対象としたものであるが、このマーキング対象のベクトルを変更した場合は、プログラム中に#Decimal number of marked vectorと記した行の配列prob_a[35]のインデックスを35から、状態ベクトルを二進数の並びと見立てその十進数化した値に変更する必要がある。
q-camgra.pyのコード
# q-cam Grover revx by Gigagulin Dec.2020
from blueqat import Circuit
import numpy as np
import qcam
import qmcn
# -------- Setting -------------------------------------------------------------------------
N=6 # number of cells
R=1 # number of registries
initial_a=np.array([0.4,0.6,0.3,0.7,0.2,0.8],dtype='float') # initial set
max_step=200 # maximum steps
stepdist_a=np.array([[0]*N]*max_step,dtype='float') # [step-number,cell-number]
probability_a=np.array([0]*N,dtype='float')
stepdist_a[0,0:N]=initial_a[0:N]
stdev_a=np.array([0]*max_step,dtype='float')
marking_prob_a=np.array([0]*max_step,dtype='float')
Reg0sb=0 # start qubit number of Reg0
Reg1sb=N # start qubit number of Reg1
Reg2sb=N*2 # start qubit number of Reg2
Reg3sb=N*3 # start qubit number of Reg3
# -------- Q-Process -----------------------------------------------------------------------
def qproc():
c.x[2,3,4].h[N-1] # qubit in x gate depends on vector you want to mark
qmcn.cccccx(c,0,1,2,3,4,5)
c.h[N-1].x[2,3,4] # qubit in x gate depends on vector you want to mark
c.h[:].x[:].h[N-1] # amplifier
qmcn.cccccx(c,0,1,2,3,4,5)
c.h[N-1].x[:].h[:]
return
# -------- final output -------------------------------------------------------------------
def fout(fstep, finitial_a,fprob_a):
sui=np.sum(finitial_a)
ave=np.average(finitial_a)
std=np.std(finitial_a)
print(' ')
print(' initial-set =',finitial_a)
print(' sum=','{0:,.2f}'.format(sui),' average=','{0:,.2f}'.format(ave),' std=','{0:,.3f}'.format(std))
for i in range(1,fstep+1):
print(' Step',i,' ','{0:,.1f}'.format(fprob_a[i]))
return
# -------- Main Body -----------------------------------------------------------------------
pstep=0
ret='y'
while ret=='y':
pstep+=1
c=Circuit(N)
qcam.propinit(N,c,initial_a)
for i in range(pstep):
qproc()
master_a=np.array(c.run())
num,vector_a,prob_a=qcam.qvextract(N,R,1,master_a)
stdev,probability_a=qcam.qcalcd(N, num,vector_a,prob_a)
qcam.qcresultout(N, pstep, num,initial_a,vector_a,prob_a,stdev,probability_a)
stepdist_a[pstep,0:N]=probability_a[0:N]
marking_prob_a[pstep]=prob_a[35]*100 #Decimal number of marked vector
stdev_a[pstep]=stdev
ret=input(' NEXT(Y/N)?')
qcam.qcfinal(N, pstep, initial_a ,stepdist_a, stdev_a )
fout(pstep, initial_a ,marking_prob_a )
qcam.qcamplot(N, pstep, stepdist_a)
⑤ステップ毎の結果の出力 qcam.qcalcd, qcam.qcresultout**
ステップ毎のコンソールへの出力は、もともとセルオートマトン用のモジュールであるqcam.qcalcd, qcam.qcresultoutを使っている。これらのモジュールに関しては、2回目の「2-4. Blueqatのベクトルと観測」を参照されたし。出力の代表例として、確率的初期状態$(0.25,0.75,0.25,0.75,0.25,0.75)$でかつマーキングは|111111>とした場合の3ステップ目の終わりのほう及び4ステップ目の結果を以下に示した。(4ステップ目の途中は中略)
ステップ毎のコンソール出力
状態ベクトルとそのベクトルの確率が一覧として表示されている。今知りたいのは|111111>の確率だすると一覧出力の64番目、つまり最後から一行前の赤枠で囲んだパーセンテージがそれである。また初めの行の Initial Cell Probability (黄枠)とは確率的初期状態で、この例の場合 $(0.25,0.75,0.25,0.75,0.25,0.75)$ である。最後の行の Final Cell Probability (黄枠)とは、そのステップまでグローバーアルゴリズムを繰り返した際に、各量子ビットにおける 1となる確率を示している。要は確率的初期状態がどう変化したかを示しておりステップ終了後の $(P_0,P_1,P_2,P_3,P_4,P_5)$ である。これ以降この各量子ビットが 1となる確率の集合をセル確率と呼ぶ。このセル確率に興味をもって説明しているグローバーアルゴリズムの図書や記事を見かけことがない。セルオートマトンではこれが正に結果である。
⑥ファイナル出力 qcam.qcfinal, qcam.qcamplot, fout
気が済むところまでステップを繰り返した後、'y' 以外の何かを入力するエスケープし、最後にまとめの結果として、各ステップでのセル確率(黄枠)及び、例えば|111111>の確率(パーセント)(赤枠)をコンソール出力し(以下の折りたたみの左)、またコンソール出力とは別に、セル確率のプロットを出力する(以下の折りたたみの右)。このプロットの横軸は第0量子ビットから第5量子ビット、つまりセルを現し、縦軸はステップ数を現している。グラフ内のグレーの四角の色の濃さが確率の大小を意味しており、確率のパーセンテージに比例した100階調のグレーで表現している。勿論、0%の時は白、100%の時は黒である。
ファイナル出力(纏め結果とプロット)
7-3. 不均一な重ね合わせからのグローバーの挙動
挙動のパターン
多くの解説で見る確率的初期状態$(0.5,0.5,0.5,0.5,0.5,0.5)$がグローバーでの最も代表的な挙動だとしよう。では、重ね合わせしていない状態ではどうだろう。例えば、$(0,0,0,0,0,0)$の場合、1が全く含まれていないが|111111>の確率は増幅されるのだろうか? あるいは $(1,1,1,1,1,1)$では? そして、全ての値が異なり、不均一に重ね合わせがされている場合、例えば$(0,0.2,0.4,0.6,0.8,1)$などでは? そこでまず、これらのステップ回数に対する|111111>の確率の変動を見てみよう。以降、全て0.5の物をhalf、全て0の物をzero、全て1の物をone、$(0,0.2,0.4,0.6,0.8,1)$をacsnedと略す。1から30ステップまでのグラフを以下に示した。
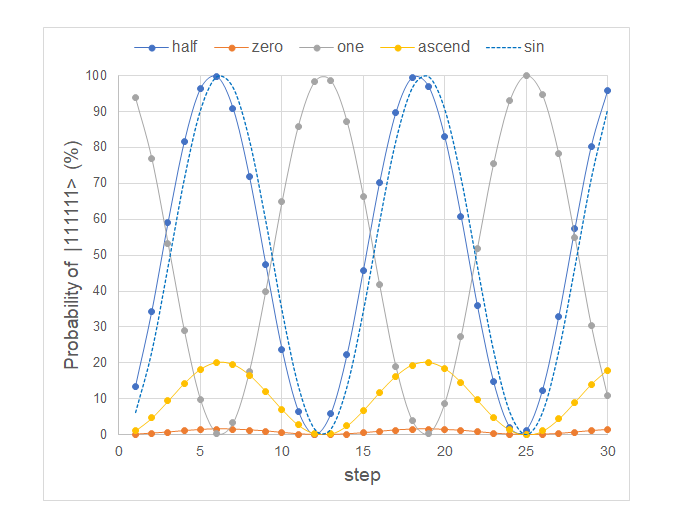
代表であるhalf(青)は見事に初めに|111111>の確率が上昇し、100%を頂点に減少に転じ0%にまで至る。それを周期的に繰り返している。zero(オレンジ)の場合ですら|111111>の確率は僅かではあるが増減するし、逆にone(灰)の場合もまた|111111>が0%になる。また、ascend(黄)も同様。また、グラフ中の青い点線は以下の式のプロット(青点線)である。ただしtはステップ数、ωは周期をTとした時、$\omega=1/T$
$$ \frac{100}{2}\biggl(1+\sin(2\omega t-\frac{1}{2})\pi\biggr)\qquad\qquad(式2)$$
実は、位相をずらすとhalf(青)と完全に重なる。つまり、サイン波である。zero、one、ascendもサイン波である。違うのは、振幅と位相だけで、周期(T)は全て同じ!ではその周期は?実は対象の量子ビット数(n)から以下の式で求められる。理屈は7-1.に記したQiita記事のリンク内の一番上または二番目を参照のこと。
$$ T=\frac{2^{n/2}}{2}\pi\qquad\qquad(式3)$$
ここではn=6なので周期は $T=2^3\pi/2=12.566$ 回である。($\omega=1/T≒0.08)$これらのことから確率的初期状態を種々変化させた時の挙動は、振幅Aと位相$\phi$を見れば掴めると言えるだろう。そこで、式3を多少入れ替えて次式で確率的初期状態を種々変化させた時の結果を検討する。
$$ \frac{A}{2}\biggl(1+\sin(0.16t-\frac{\phi}{2})\pi\biggr)\qquad\qquad(式4)$$
位相Φの意味 =最適増幅回数
式4から明らかなように $t=0$ かつ位相 $\phi=1$ の時 0 (確率0%)である。このゼロから半周期(=T/2=6.28回)分tが進と、最大値Aまで増幅されることを意味する。逆に位相 $\phi=-1$では、 $t=0$ の時、既に最大振幅にあり、tが進むと減衰することを意味している。つまり、位相の大小により増幅可能な最大値までの最適増幅回数を知ることができる。グローバーアルゴリズムの最適増幅回数 $i_{op}$ は次式となる。ただし、⌊ ⌋は床関数。
$$i_{op}= ⌊\frac{T}{4}(\phi+1)⌋\qquad\qquad(式5)$$
並び順を変えたら
前述のascendで並び順をかえたらどうなるだろう?例えば$(0.4,0.6,0.2,0,1,0.8)$のように。先ほどとは少し気分を変えて|110101>での増幅で確かめてみる。ascendの場合を式4でフィッティングさせると、A=20.1、$\phi=1$である。では、$(0.4,0.6,0.2,0,1,0.8)$をフィッティングさせると、A=20.1、$\phi=1$であり、ascendと同じである。さらに$(1,0.8,0.6,0.4,0.2,0.1)$でもA=20.1、$\phi=1$である。 次に、増幅対象のベクトルの並びを変えたらどうなるか。そこで|110101>を|111010>にしてascendの場合を計算してみた。すると、A=23.1、$\phi=0.35$となるが、$(0.4,0.6,0.2,0,1,0.8)$と$(1,0.8,0.6,0.4,0.2,0.1)$では先と同じA=20.1、$\phi=1$となる。何故こうなるのかや法則は未だ検討しておらず今後の宿題としたい。
マーキング対象のベクトルを変えたら
前項で増幅対象のベクトル、つまりマーキングするベクトルの並びだけ変えてみたが、並び以外にも異なるベクトルとした場合、何が起このるのだろうか。全64個の状態ベクトル全てで、同じ確率的初期状態からどのような挙動の差を呈するのか調べればよいのだが手間である。そこで代表として状態ベクトル中の1の数、つまり和が0~6で代表的なベクトルとして、次の7種類で検討してみる。
$$0: |000000> , 1: |000010>, 2: |010010>, 3: |100011>, 4: |111010>, 5: |111101>, 6: |111111>$$
これに対して確率的初期状態として、$(0.5,0.5,0.5,0.5,0.5,0.5)$のように全て同値とし、要素の和が0,0.4, 1, 2, 3, 4, 5, 5.6,6と変化させたものを、それぞれ7種類のターゲットベクトルへの増幅がどのようになるのかを調べてみた。結果は以下の折りたたみ。
結果
すぐに分かることとして確率的初期状態の和(以降sum)が3、つまり要素が全て0.5である場合、つまり均一重ね合わせの場合、マーキング対象のベクトルに無関係にA=100、$\phi=0.86$であることが挙げられる。またマーキング対象のベクトル要素和が3: |100011>の時、sum=3に対して振幅Aと位相$\phi$ともに左右対称である。(下図の左)振幅に関してはベクトル要素和が1,2,4,5は3と同じく左右対称に見えるが、よく見ると左右対称ではなく歪んでいる。そして0と6では非対称性は極端に大きい。直感的に言えば、確率的初期状態が均一重ね合わせからかけ離れるほど非対称性が大きい。

振幅、位相ともマーキング対象のベクトル和が3のようにそれ自身でsum3に対して対称ではないが、2と4の組、1と5の組、0と6の組でミラーとなっている。また、位相$\phi$の変化域が、いま述べた組の順で大きくなっている。後述するが振幅の左右対称からのズレと位相の変化には関連がある。
確率的初期状態のバラツキ度をかえたら
確率的初期状態$(P_0,P_1,P_2,P_3,P_4,P_5)$の特徴的パラメータとして前述した $sum=\sum P_i$ : 0≦sum≦6 の他に標準偏差(母集団)、つまりバラツキ (0≦σ≦0.5) を変化さたらどのような挙動となるのだろう? マーキング対象のベクトルは、前述した通り最も位相がダイナミックに変化する|111111>とした。
●データセット
sumは、0,0.4, 1, 2, 3, 4, 5, 5.6,6、また σ はそれぞれのsumで、σ=0からとり得る最大のσまで0.05刻みでデータセットを作成した。そのデータセットは、Githubのリポジトリ q-cams内に grover-data.xlsx というエクセルファイル内のinitial-data-setと言うシートに格納している。
●結果
全ての結果と式4でフィッティングさせた振幅Aと位相$\phi$もGithubのリポジトリ q-cams内に grover-data.xlsx というエクセルファイル内のsum**(**は数値)と言うシートに格納している。また、確率的初期状態のsumとσに対する振幅Aと位相$\phi$の値をまとめた表と、同じくsumとσに対する最適増幅回数の結果及び$\phi$から式5で計算されれた最適増幅回数の表を以下の折りたたみ内に掲載した。
振幅Aと位相$\phi$のsumとσに対する依存性
Fig.1は確率的初期状態のsumを横軸に、振幅(A)つまり最大に増幅された時の|111111>の確率(%)を縦軸にしたグラフ。sum3がどの標準偏差σのときでも最大で左右対称に見えるがσの値が低く、かつsum>5以上の所で対称性が崩れている。(後述)
Fig.2はFig.1と同様のものであるが横軸にσ、縦軸に振幅をとったグラフである。sum=1のσ=0.25で怪しい点がでているものの、概ね振幅は標準偏差が大きくなるにつれ、つまり$P_i$の値のバラツキが大きくなにつれ、振幅(最大増幅確率)は単調に減少している。また、σ=0での各sumにおける上下関係は、σが変化しても逆転しない。
Fig.3は確率的初期状態のsumを横軸に、位相$\phi$を縦軸にしたグラフである。標準偏差σによる差は小さく、全てでsum<3で、位相が1で、それ以上の区間では上昇に伴い、$\phi$は減少している。さらにsum=5以上では負になっている。位相が負になっているsumの値では、前述した振幅(A)のsum=3に対する対称性が崩れている。
Fig.4は横軸にσ、縦軸に位相 $\phi$ をとったものである。sum=5はちょうど位相が0近傍でやや挙動不審であるが、他は位相が正の時は、σ増加で増加傾向で1に近づき、位相が負では逆で減少し-1に近づいていく。
対称性からのズレ
位相が1から下がるにつれて振幅(A)を対称性から想定される値よりも大きめにする傾向が認められる。それを確かめるために、対称性からのズレと言う意味での g (gap from symmetry)を、sum=3を対象軸にして、ある3未満のsumの値xの確率% $A_x$ と,sumが6-xの確率% $A_{6-x}$とした場合、$ g=A_{6-x}-A_x$ と定義する。Fig.5 (σ=0の場合)を参照されたし。
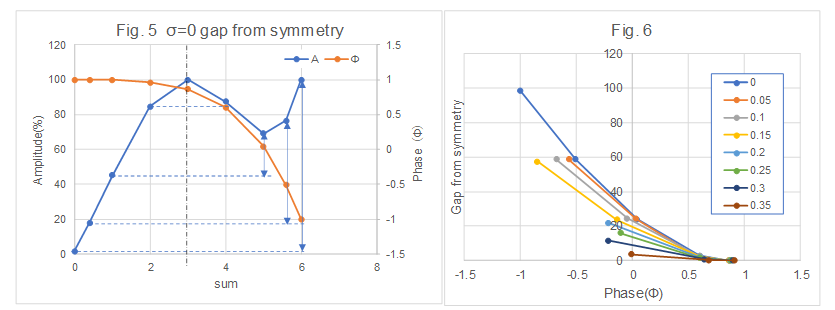
位相 $\phi$ と先に定義したgの関係をプロットしてみたグラフをFig.6に示した。このグラフが示している通り、位相が1から下がるにつれて振幅(A)を対称性から想定される値よりも大きめにする傾向が認められる、$\phi=-1$に至り最高確率に至る。当然ではあるが、oneであれば|111111>の確率(%)は100%である上、それは $\phi=-1$ で $i_{op}=0$ である。
7-4. サマリー
サマリーと言うよりはエクスキューズ?
挙動のまとめ
不均一重ね合わせの確率的初期状態からのグローバー適用では
●均一重ね合わせと同様、振幅はサイン波となる。周期も均一と同様、量子ビット数から得られ、他のパラメータには依存しない
●位相の大小により増幅可能な最大値までの最適増幅回数を知ることができる
●位相の大小は対称性のズレに関わるが、多分、それは確率的初期状態が均一重ね合わせからかけ離れるほど非対称性が大きい
●並び順に関して・・・概ね並び順に関する影響は少ないが、マーキング対象ベクトルとの兼ね合い等で変化するようである。実は5回目の渋滞系セルオートマトンの時も緩和時間と確率的初期状態の並びの関連を説明できなかった
●マーキング対象のベクトルを変えた場合、そのベクトル要素和が3では振幅、位相ともsum=3で対称だが、ベクトル要素和2と4、1と5、0と6の 対でミラーとなっている
●バラツキ度をかえた場合、同じsumであってもバラツキが大きくなると振幅は単調に減少していく。また、σ=0での各sumにおける上下関係は、σが変化しても逆転しない
●対称性から想定される値と実際の値との差異は位相差と明確な関係が認められる
挙動予測に関して
グローバーアルゴリズムの数理からアプリオリに挙動を予測できれば良いのだが、1回目で申した通り門外漢故、それは能力のスコープ外。そのため、せいぜいデータから帰納的に、と言うかある関数を過程して多重フィッティングするだけとなってしまう。それでも種々トライし結果を得ているのだが、それは、まるで機械学習させたのと同じようで、アルゴリズムが持つ数理からの演繹的な説明ができなく虚しい。それ故、ここでの紹介はやめることにした・・・弁解
以上!