Groverアルゴリズムで15を因数分解

#はじめに
###初めての投稿
はじめまして、一昨年に55歳から趣味で量子コンピュータの勉強を始めたSE歴3x年の平凡なSEです。量子コンピューター、線形代数、量子力学はいずれもド素人ですが、マイペースで勉強しています。
量子プログラミングの勉強は書籍やネットの情報を参考に IBM Q Experience の Circuit Composer 上で行なっています。
今回人生初めての投稿になりますが、とにかくアウトプットしてみるということから挑戦しようと思いますので、よろしくお願いします。

(2020/03/16 追記)
Groverアルゴリズムの解説については、私が参考にした、もしくは投稿後に参考になったリンクを関連情報に掲載し、時々更新しています。

###投稿概要
ご紹介する回路は、今年ようやく自分がGroverアルゴリズムの使い方を理解してから2番目に作ったGrover回路(プログラム)で、自分の理解が合っているかを試す目的で作りました。因数分解を高速に行うことは目的としていませんので、ご了承ください。(「因数分解」で期待した人、ごめんなさい。 )

今回は、とにかく投稿を始めようということで、ざっと全体像についてご説明しようと思います。

(2021/3/3 追記)
『旧石器人(デジタリアン)がグローバー回路と使い方を(我流で)習得するまで(笑)』に、この回路を作れるようになるまでの過程を投稿しました。

(2019/12/25 追記)
Groverアルゴリズムの使い方を理解して最初に作ったGrover回路(プログラム)についても『Groverアルゴリズムで実際にデータを検索(!?)』に投稿しました。

###Groverで因数分解しようと思った理由
Groverのサンプルプログラムとして紹介されているものは、「解が分かっている前提」でマーキングして振幅増幅するものばかりで、数式などの解説を理解できない素人には何をしているのかが理解できずにフラストレーションを感じていました。なので、例として15の因数分解をサンプルとして示せれば、私のような素人にもGroverアルゴリズムの「使い方」のイメージが把握できるのではと考えました。

###着想
15の因数分解がGroverで意外と簡単に実装できそうと思ったのは以下の理由からです。

1. 15の因数分解は一方の因数が4未満(2bit)になるので、5bit=3bit×2bitとすると解がユニークに決まる。
2. 3bit×2bitの乗算回路なら、シフトと加算(=加算のみ)で簡単に作れる。

15の因数分解というと何だか量子アルゴリズムのHello World!みたいで、サンプルの一つとして丁度良いかな(?)とも思っています。

#回路(プログラム)の説明
###処理概要
15の因数分解を掛け算の総当たりで探すというベタな方法で行います。これでは√Nまでの全ての数で割っているのと同じなので**「全く速くありません」が、少なくともサンプルとしてやっていることがシンプルで「解が分かっている前提」の感じは取り除ける**のではと思っています。

15以外にも10=5×2、14=7×2、15=5×3、21=7×3などの因数分解ができるはずです。(mod計算を行う量子回路を使うことができれば$\sqrt[4]{N}$までのスピードアップもできると思います。)

###処理の構成

1. 初期化(アダマールゲートでの5bitの重ね合わせ状態の作成と因数分解する15のセット)
2. シフト&加算による3bit×2bit=5bitの乗算回路
3. 5bitの比較回路
4. 正解(比較一致時)の位相(符号)反転
5. 3.と2.のアンコンピュート
6. 5bitの振幅増幅
7. 2.〜6.を適正回数(5bitの振幅増幅の場合、合計4回)繰り返す
8. 結果の測定

###回路イメージ
以下の例では１サイクルだけ実行して測定していますが、実際には乗算回路から振幅増幅までを４サイクル繰り返してから測定すると(ほぼ)100%の確率で正解を得ます。

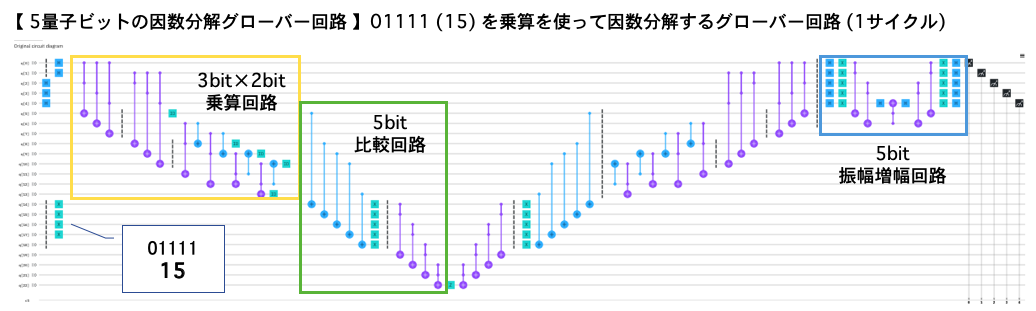
※振幅増幅で制御4bitの制御notを作るのに、作業bitとしてアンコンピュートして|0>に戻っているq[5]、q[6]をそのまま再利用しています。(ビジュアル重視(?)で実効性は無視)

#実行結果
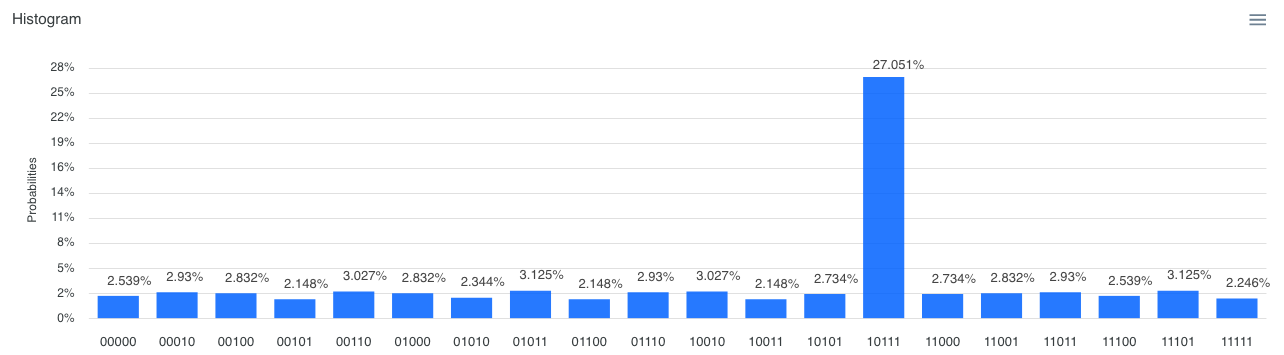
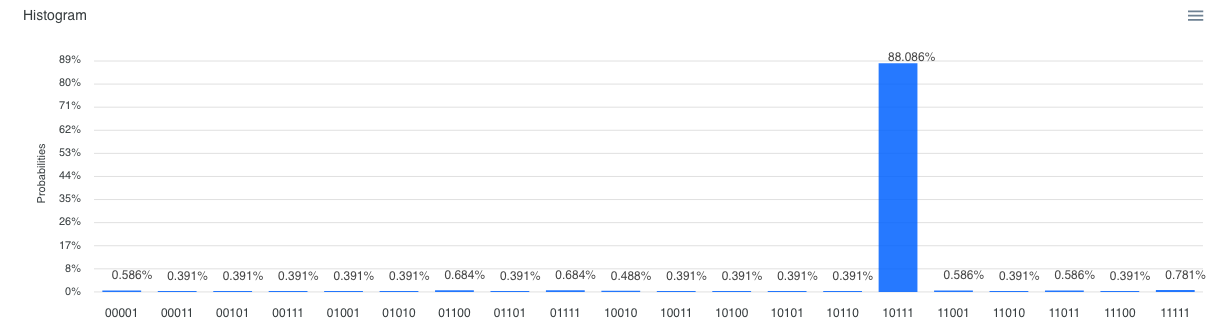
正解の15=5×3は、3bit×2bit で 0x10111 となります。5bit(N=32)の振幅増幅で解が一つの場合、グローバー回路の適切な繰り返し回数は4回です。以下に1回から5回までの繰り返し回数で実行した時の実行例を添えます。
###繰り返し回数 : 1回(約27%)

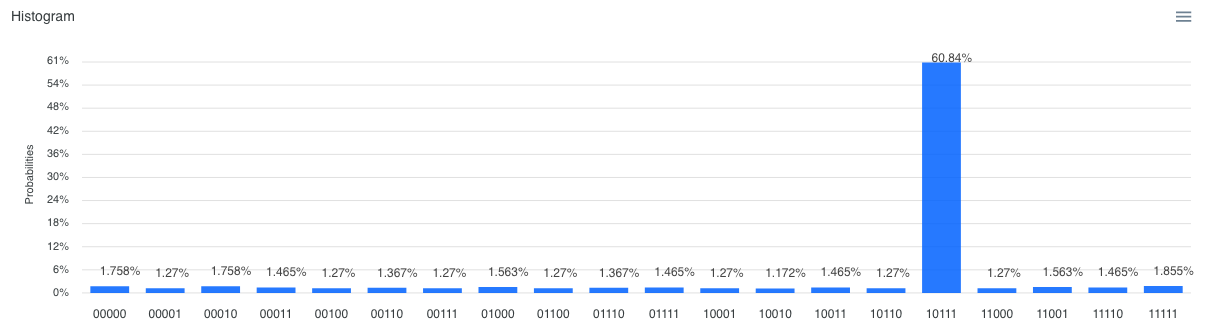
###繰り返し回数 : 2回(約61%)

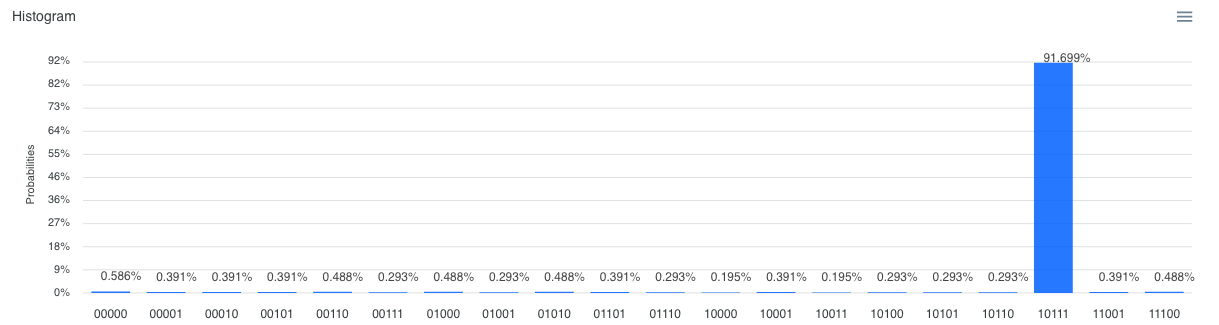
###繰り返し回数 : 3回(約92%)

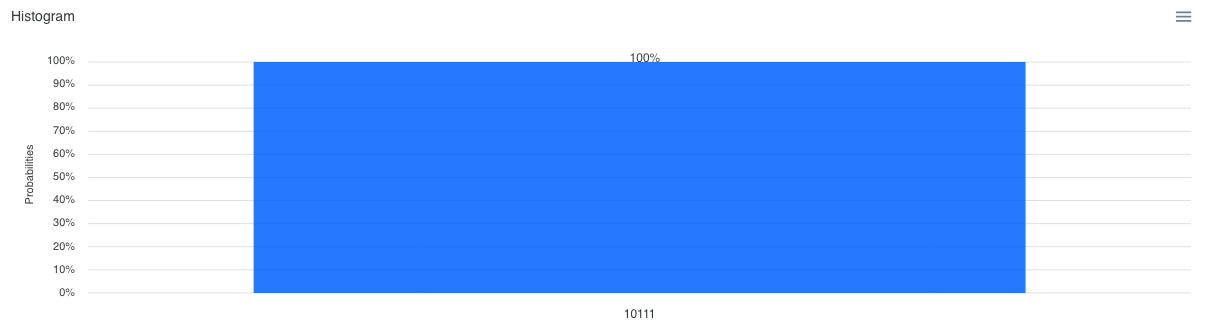
###繰り返し回数 : 4回(約100%)

###繰り返し回数 : 5回(約88%)

#CODE
参考までに1サイクルだけ実行する場合のコードを掲載します。

OPENQASM 2.0;
include "qelib1.inc";

qreg q[23];
creg c[5];

barrier q[0],q[1];
h q[2];
h q[3];
h q[4];
barrier q[14],q[15],q[16],q[17],q[18];
h q[0];
h q[1];
x q[14];
x q[16];
x q[17];
barrier q[0],q[1],q[2],q[3],q[4];
ccx q[0],q[2],q[5];
ccx q[0],q[3],q[6];
ccx q[0],q[4],q[7];
barrier q[5],q[6],q[7];
ccx q[1],q[2],q[8];
ccx q[1],q[3],q[9];
ccx q[1],q[4],q[10];
id q[5];
barrier q[8],q[9],q[10];
ccx q[6],q[8],q[11];
cx q[6],q[8];
ccx q[7],q[9],q[12];
cx q[7],q[9];
id q[8];
ccx q[9],q[11],q[12];
cx q[11],q[9];
id q[9];
ccx q[10],q[12],q[13];
cx q[12],q[10];
id q[13];
id q[10];
barrier q[10],q[5],q[6],q[7],q[8],q[9],q[11],q[12],q[13];
cx q[5],q[14];
x q[15];
cx q[8],q[15];
cx q[9],q[16];
cx q[10],q[17];
cx q[13],q[18];
x q[14];
x q[15];
x q[16];
x q[17];
x q[18];
barrier q[14],q[15],q[16],q[17],q[18];
ccx q[14],q[15],q[19];
ccx q[16],q[17],q[20];
ccx q[18],q[19],q[21];
ccx q[20],q[21],q[22];
z q[22];
ccx q[20],q[21],q[22];
ccx q[18],q[19],q[21];
ccx q[16],q[17],q[20];
ccx q[14],q[15],q[19];
barrier q[14],q[15],q[16],q[17],q[18];
x q[14];
x q[15];
x q[16];
x q[17];
x q[18];
cx q[13],q[18];
cx q[10],q[17];
cx q[9],q[16];
cx q[8],q[15];
cx q[5],q[14];
barrier q[13],q[12],q[11],q[9],q[10],q[8],q[7],q[6],q[5];
cx q[12],q[10];
ccx q[10],q[12],q[13];
cx q[11],q[9];
ccx q[9],q[11],q[12];
cx q[7],q[9];
ccx q[7],q[9],q[12];
cx q[6],q[8];
ccx q[6],q[8],q[11];
barrier q[8],q[9],q[10];
ccx q[1],q[4],q[10];
ccx q[1],q[3],q[9];
ccx q[1],q[2],q[8];
barrier q[5],q[6],q[7];
ccx q[0],q[4],q[7];
ccx q[0],q[3],q[6];
ccx q[0],q[2],q[5];
barrier q[0],q[1],q[3],q[2],q[4],q[5],q[6];
h q[0];
h q[1];
h q[2];
h q[3];
h q[4];
x q[0];
x q[1];
x q[2];
x q[3];
x q[4];
ccx q[0],q[1],q[5];
ccx q[2],q[3],q[6];
h q[4];
ccx q[5],q[6],q[4];
h q[4];
ccx q[2],q[3],q[6];
ccx q[0],q[1],q[5];
x q[0];
x q[1];
x q[2];
x q[3];
x q[4];
h q[0];
h q[1];
h q[2];
h q[3];
h q[4];
measure q[0] -> c[0];
measure q[1] -> c[1];
measure q[2] -> c[2];
measure q[3] -> c[3];
measure q[4] -> c[4];

#終わりに
今回、この記事が私の最初の記事になります。不慣れな点が多いので、アドバイスなど頂けると幸いです。
今後は、文章や記述方法などの表現の仕方についても、皆さんの記事を参考に勉強していきたいと思います。
よろしくお願いします。

#参考文献

1. 中山茂『クラウド量子計算入門』
2. 中山茂『Python 量子プログラミング入門』

#関連情報

1. Groverアルゴリズムで実際にデータを検索(!?)
2. IBM Quantum Computing で計算してみよう
3. @YuichiroMinato『Grover（グローバー）のアルゴリズム』
4. @kyamaz『Grover アルゴリズムについて』
5. @shiibass『グローバーのアルゴリズムの量子回路を組む』
6. 慶應義塾Keio University『量子コンピュータ授業 #4　グローバーのアルゴリズム』
7. 物理とか『Grover の検索アルゴリズム と Quantum Amplitude Amplification/Estimation』
8. @kyamaz『量子コンピュータで因数分解が高速に解ける？〜 ショアのアルゴリズム 〜』
9. @SamN『量子アルゴリズムの基本：Groverのアルゴリズムの確認』
10. IBM Quantum Challenge 2019 『Week1 量子回路における加算器』
11. blueqatで4qubitのGloverのアルゴリズム
12. 旧石器人(デジタリアン)がグローバー回路と使い方を(我流で)習得するまで(笑)

#更新履歴
2019/12/06 初版
2019/12/09 参考文献の追加とタイプミスの訂正
2019/12/13 関連情報欄を追加(参考文献と合わせて適宜更新予定)
2019/12/20 関連情報追加
2019/12/24 訂正(回路イメージの但し書き、「制御5bitの制御NOT」を4bitに)
2019/12/25 参考情報9.-10.追加
2020/03/16 関連情報追加
2020/09/18 微修正(Groverアルゴリズムの**「使い方」**のイメージが把握できるのでは)
2020/10/29 微修正(数式表現N^(1/4)→$\sqrt[4]{N}$)
2021/03/03 「旧石器人(デジタリアン)がグローバー回路と使い方を(我流で)習得するまで(笑)」のリンク追記