More than 3 years have passed since last update.

Groverアルゴリズムで実際にデータを検索(!?)

Last updated at 2021-03-03Posted at 2019-12-19

#はじめに
昨日、「Groverアルゴリズムで15を因数分解」で静かにQiitaデビューして今回が2回目の投稿になります。今回も、ド素人による素人のための**Groverシリーズ第2弾(笑)**ということで、Groverアルゴリズムでデータ検索を行う実験回路(プログラム)と実際に作ってみての気づきについて投稿します。

今回は(も?)、細かい理論はスッ飛ばして全体像を見てイメージを掴んで頂く事が出来たら私的には目標達成ですが、アドバイス、コメントなどが頂ければ幸いです。また、アルゴリズムを正しく理解している人には、素人が引っかかるポイントについて知って頂ければ幸いです。

(2020/03/16 追記)
Groverアルゴリズムの解説については、私が参考にした、もしくは投稿後に参考になったリンクを関連情報に掲載し、時々更新しています。

###Groverでデータ検索をしてみようと思った理由
Groverアルゴリズムというと、1996年に発表された時のタイトルのせいで多くの場合**「データベース検索」と紹介され、電話帳のようなイメージで説明されることが多いです。しかし、例として紹介されるプログラム(回路)はというと「これから探すはずの索引番号にマーキング」して振幅増幅するものばかりで、理論を理解する前の素人には「一体何がしたいんだ」**状態でフラストレーションを感じていました。(同じ思いの初心者は多いと思います)

そんな訳で、線形代数とか数式が苦手な私がIBM Q ExperienceのCircuit Composerで試行錯誤しながら2bitのサンプルGrover回路を読解してGroverアルゴリズムの使い方(回路の作り方)を理解した時に、まず一番最初に試しに作ろうと思ったのが**「実際にデータを検索する」**Grover回路です。

(2021/3/3 追記)
『旧石器人(デジタリアン)がグローバー回路と使い方を(我流で)習得するまで(笑)』に、この回路を作れるようになるまでの過程を投稿しました。

###問題設定
今回はGroverアルゴリズムで実際にデータを検索してみることだけが目的です。余分なチェックロジックとかを不要にするために、検索するデータには重複が無いようにユニークなデータを登録し、検索条件にも存在するデータのみを指定する前提とし、最小構成として索引が2bit、データが3bitでのデータ探索を実装することにします。索引2bitでデータ1件の場合のGroverの適正な繰り返し回数は1回で、確率100%でデータの格納されている索引番号を得る事が出来ます。

###着想
データベースをどのように量子回路で実装するかですが、今回はデータベースと言っても**「データの検索(=READ)のみ」で更新とかの必要がありませんので、索引をアドレスとして各アドレスに対応するデータが格納された「ROMをイメージ」**しました。

具体的にはアドレス2bit、データ3bitでアドレス毎に対応するデータを出力するようデータをROMのように直接焼き付ける感じ(ハードコーディング)で量子回路を簡単に作ります。

#回路(プログラム)の説明

###処理概要
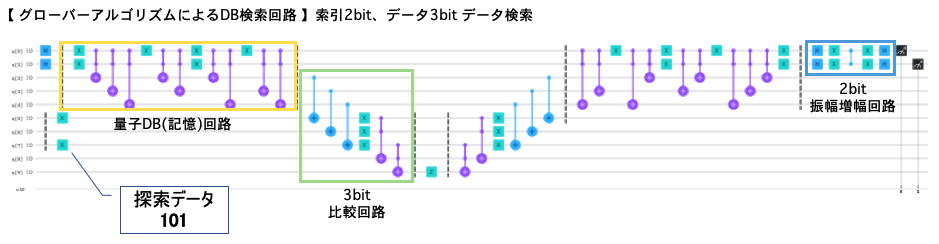
検索対象のデータは、索引00、01、10、11に対応して以下の4件とし、検索条件はデータ＝101 (実際は以下のどのデータでも可) とします。

索引	データ
00	111
01	011
10	101
11	110
量子DB(データ記憶)回路は、q[1]〜q[0]の2bitを索引、q[4]〜q[2]の3bitをデータに割り当て、制御NOTゲートを用いて索引に対応したデータが出力されるように作ります。

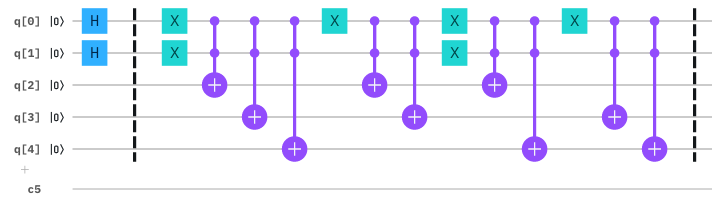
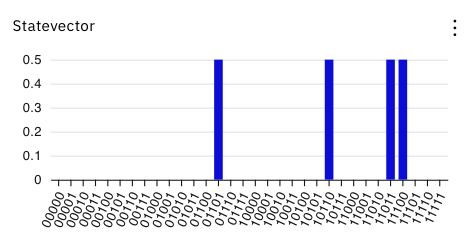
この回路の索引(q[1]〜q[0])にアダマールゲートを用いて00〜11の重ね合わせ状態を入力すると、上記の4件の索引とデータの組が重ね合わせ状態として出力され、検索条件と全データの比較を一度にまとめて行う事ができるようになります。

このROMイメージのデータベース(READ ONLY)のデータ(q[4]〜q[2])と検索条件のデータ(q[7]〜q[5])を比較して、一致した時(q[9]=	1>)にマーキングして振幅増幅するように回路を構成します。

###処理の構成

アダマールゲートで00から11までの全索引の重ね合わせ状態を作成
索引に対応するデータを出力する(量子ROM)回路
検索条件とデータ3bitの比較回路
データが検索条件と一致した時の位相(符号)反転(=マーキング)
3.と2.のアンコンピュート
2bitの振幅増幅
結果の測定

ここでのポイントは、ステップ3.で比較するのは3bitの検索条件とデータのみで索引は比較の対象では無い(答えとなる索引番号を知っていてマークするわけでは無い)ことです。

###回路イメージ

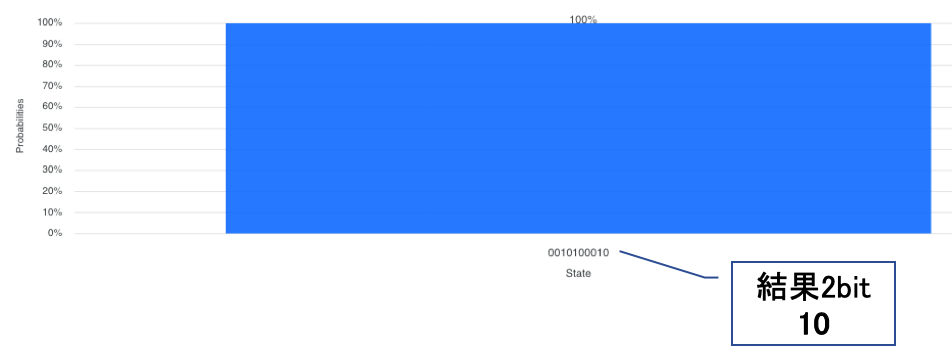
#実行結果
探索条件としてq[7]〜q[5]の3bitにセットした「探索データ101」が格納されている索引番号(アドレス)として実行結果のq[1]〜q[0]の2bitに「10」を得る事ができています。

#実際に作ってみて疑問に思ったこと
###高速データベース検索だとぉ!?
ここまで試したところで、「ド素人」の私は次の疑問にぶち当たりました。

「Groverアルゴリズムは、本当に電話帳のようなデータベースの(単純)検索に有効なのか!?」

出来上がった回路を眺めての第一印象は、答えの「10」に直接マーキングこそしていないものの、通常のデータベースで言うと**「全データをロード(全件インポート)」**しているみたいで、確かに三分クッキングかも知れないけど下ごしらえに一時間かかっているように思えました。

今回、Groverアルゴリズム自体の細かい説明は省略しますが、一般にグローバーの繰り返し(イテレーション)の中で毎回データを索引に紐付けてから比較&マーキングし、索引とデータの紐付けを解除してからマーキングされた索引を振幅増幅する必要があり、しかもこれを約√N回繰り返すことになります。

これでは、データが大量になればなるほど、単純検索には向いてないとしか思えません。

###高速に索引とデータを紐付ける方法は?
グローバーの繰り返しで毎回データを全件ロードしていたのでは、データ検索の部分がいくら高速だと言われても意味がなくなるので、グローバーの繰り返しの中で高速に索引とデータを紐付けて重ね合わせ状態を作る方法を考えなければなりません。そのためには並列で ... 例えば、RAMの各メモリーセル(bit)上に量子ビットを配置して倍々にマージしていけば2^n個のデータをnステップで重ね合わせれるのですが、これをGroverアルゴリズムを用いて高速検索したいほどの大規模データベースに対して行うには ...

いやいや、慌てるな。まあ、落ち着け!! > 俺

きっと、良いアルゴリズムや工夫があるに違いない。との思いで試行錯誤したりネットで探すという悶々とした日々(笑)を過ごしていたのですが、数ヶ月経ってついに、背伸びして手を出した**ニールセン&チャンの本(参考文献1.と2.)の第6章"6.5 Quantum search of an unstructured database"**にこの件についての解説と見解があるのを見つけました。(幸い、この節に限り(?)数式が殆ど無い! )

こうして無事(?)、やっぱりそうですよね〜orzっと納得してGroverで高速にデータベースの(単純)検索をするための索引とデータの紐付け方や、複製ができないような量子データベースについて考えるのを(一旦)止めることができました。

#終わりに
"A fast quantum mechanical algorithm for database search"、第一印象・ネーミングの影響って大きいですね。

Groverアルゴリズムは、素人目に見てもデジタルで判定ロジックが書ける探索問題全般に使える汎用性を持っている反面、実は単純なデータ検索には全くと言っていいほど向いていないにも関わらず、素人の初学者には真逆にデータベース専用のアルゴリズムとさえ誤解される事が多いのでは無いでしょうか。

もはや量子コンピュータは理論や思考実験の世界のものではなくエンジニアリングの対象だと思いますし、ニールセン先生&チャン先生の本が出てからでも既に約20年も経っています。

"上級者の皆さん、量子コンピュータ素人のIT技術者にGroverアルゴリズムを『データベース検索』のアルゴリズムと紹介するのは止めませんか?"

一般のIT技術者にとってデータベースという言葉は、OracleとかDB2とか具体的なイメージに直結して強い先入観を与えてしまいますので。

#CODE
OPENQASM 2.0;
include "qelib1.inc";

qreg q[10];
creg c[10];

h q[0];
h q[1];
barrier q[5],q[6],q[7];
barrier q[0],q[1],q[2],q[3],q[4];
x q[5];
x q[7];
x q[0];
x q[1];
ccx q[0],q[1],q[2];
ccx q[0],q[1],q[3];
ccx q[0],q[1],q[4];
x q[0];
ccx q[0],q[1],q[2];
ccx q[0],q[1],q[3];
x q[0];
x q[1];
ccx q[0],q[1],q[2];
ccx q[0],q[1],q[4];
x q[0];
ccx q[0],q[1],q[3];
ccx q[0],q[1],q[4];
barrier q[2],q[3],q[4],q[1],q[0];
cx q[2],q[5];
cx q[3],q[6];
cx q[4],q[7];
x q[5];
x q[6];
x q[7];
ccx q[5],q[6],q[8];
ccx q[7],q[8],q[9];
barrier q[5],q[6],q[7],q[8],q[9];
z q[9];
barrier q[7],q[6],q[5],q[8],q[9];
ccx q[7],q[8],q[9];
ccx q[5],q[6],q[8];
x q[5];
x q[6];
x q[7];
cx q[4],q[7];
cx q[3],q[6];
cx q[2],q[5];
barrier q[2],q[1],q[3],q[4],q[5],q[0];
ccx q[0],q[1],q[4];
ccx q[0],q[1],q[3];
x q[0];
ccx q[0],q[1],q[4];
ccx q[0],q[1],q[2];
x q[0];
x q[1];
ccx q[0],q[1],q[3];
ccx q[0],q[1],q[2];
x q[0];
ccx q[0],q[1],q[4];
ccx q[0],q[1],q[3];
ccx q[0],q[1],q[2];
x q[0];
x q[1];
barrier q[0],q[1],q[2],q[3],q[4];
h q[0];
h q[1];
x q[0];
x q[1];
cz q[0],q[1];
x q[0];
x q[1];
h q[0];
h q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];
measure q[2] -> c[2];
measure q[3] -> c[3];
measure q[4] -> c[4];
measure q[5] -> c[5];
measure q[6] -> c[6];
measure q[7] -> c[7];
measure q[8] -> c[8];
measure q[9] -> c[9];

#参考文献

Nielsen, M.A. and Chuang, I.L., Quantum Computation and Quantum Information, 2010, Cambridge University Press.
ミカエルニールセン、アイザックチャン『量子コンピュータと量子通信〈2〉量子コンピュータとアルゴリズム (量子コンピュータと量子通信 2)』

#関連情報

#更新履歴
2019/12/20 初版
2019/12/24 微細修正(言葉足らずだったところ)
2019/12/25 関連情報9.-14.追加
2020/03/16 関連情報15.追加
2020/05/19 処理概要に量子DB(READ ONLY)の回路と重ね合わせ状態のstatevector表示を追記
2021/03/03 「旧石器人(デジタリアン)がグローバー回路と使い方を(我流で)習得するまで(笑)」のリンク追記

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up